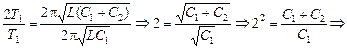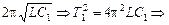 Рис. 15.4 Рис. 15.4 |
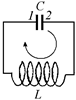
Попробуем выяснить, как зависят от времени заряд на обкладке конденсатора и сила тока в колебательном контуре (рис. 15.4). Но прежде, чем мы приступим к вычислениям, отметим следующее:
1) ток в процессе колебаний течет то в одном, то в другом направлении. Чтобы величина силы тока в данный момент времени была определена однозначно, необходимо задать направление обхода контура. Тогда ток, текущий вдоль направления обхода, считаем положительным, а против – отрицательным;
2) заряды на пластинах конденсатора всегда равны по величине и противоположны по знаку, поэтому надо договориться, заряд какой пластины (1 или 2) в данный момент мы рассматриваем;
3) напряжение между пластинами конденсатора – это разность между потенциалами пластин. Эта величина, как и сила тока, меняет знак в процессе колебаний. Чтобы величина была однозначно определена в данный момент времени, договоримся, что мы считаем напряжением U = j1 – j2 или U = j2 – j1, где j1 и j2 – потенциалы пластин 1 и 2 соответственно.
С учетом данных замечаний приступим к установлению зависимости от времени заряда q(t), тока i(t) и напряжения и(t):
1) зададим направление обхода контура по часовой стрелке (см. рис. 15.4);
2) назовем «первой» ту пластинку конденсатора, которая встретилась первой после катушки при следовании по направлению обхода контура, а «второй» – смежную с ней пластину. Зарядом конденсатора будем называть заряд первой пластины;
3) под напряжением будем понимать величину U = j1 – j2. Если q1 > 0, а q2 = –q1 0. Но величина Dq может быть и отрицательной, если ток в данный момент времени t течет против направления обхода, тогда i(t) –5 с. При подключении параллельно конденсатору контура дополнительного конденсатора электроемкостью 3,0×10 –8 Ф период колебаний увеличился в два раза. Определите индуктивность катушки и начальную электроемкость конденсатора колебательного контура.
| Т1 = 1,0×10 –5 с С2 = 3,0×10 –8 Ф Т2/Т1 = 2 | Решение. Вспомним, что при параллельном соединении емкости конденсаторов складываются, и применим формулу Томсона для обоих случаев: Т1 =  , (1) 2Т1 = , (1) 2Т1 = 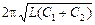 , (2) , (2) |
| L = ? C1 = ? |
Разделим (2) на (1) и получим
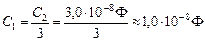
Выразим индуктивность L из (1):
Т1 =
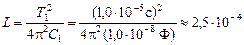
Ответ: 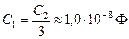
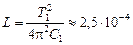
СТОП! Решите самостоятельно: В4–В6, С3–С5.
Задача 15.3. Колебательный контур состоит из катушки индуктивностью L = 0,20 Гн и конденсатора емкостью С = 1,0×10 –5 Ф. Конденсатор зарядили до напряжения U = 2,0 В, и он начал разряжаться. Каким будет ток в момент, когда энергия контура окажется поровну распределенной между электрическим и магнитным полем?
| L = 0,20 Гн С = 1,0×10 –5 Ф U = 2,0 В Wм = Wэ | Решение. Энергия контура равна 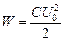 . В тот момент, когда энергии электрического и магнитного полей равны, на долю энергии магнитного поля приходится ровно половина полной энергии контура, поэтому . В тот момент, когда энергии электрического и магнитного полей равны, на долю энергии магнитного поля приходится ровно половина полной энергии контура, поэтому |
| i = ? |
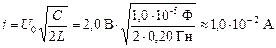
Ответ: 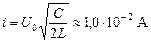
СТОП! Решите самостоятельно: А5–А7, В7–В9.
Задача 15.4.Заряд q на пластинах конденсатора колебательного контура изменяется с течением времени t по закону q = =10 -6 cosl0 4 pt. Записать закон зависимости силы тока от времени i(t). Найти период и частоту колебаний в контуре, амплитуду колебаний заряда и амплитуду колебаний силы тока. Все величины считать точными и заданными в единицах СИ.
| q = 10 -6 cosl0 4 pt | Решение. Воспользуемся формулой (15.3) i(t) = = q¢(t): i(t) = (10 -6 cosl0 4 pt)¢ = 10 -6 (–sinl0 4 pt)×10 4 p = = –10 –2 psin10 4 pt. |
| i(t) = ? T = ? f = ? qm = ? im = ? |
Учитывая, что q = qmcoswt, а i = –imsinwt, легко находим значения заряда и тока:
Находим амплитуду колебаний заряда и амплитуду колебаний силы тока:
w = 10 4 p Þ 
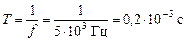
im = 10 –2 p А; w = 5×10 3 Гц; 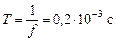
Видео:Графические зависимости заряда и силы тока от времени в идеальном колебательном контуре. 11 класс.Скачать

Дисциплина: Физика тема: 060 Механические колебания и волны (стр. 5 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
3)
4) Знак 
17. [Уд1] (ВО1) Направления индукционного тока в контуре и магнитного поля (к нам) указывают, что для величины магнитной индукции справедливо соотношение
1)
2)
3)
4) Знак 
18. [Уд1] (О) При движении рамок в однородном магнитном поле в направлениях, указанных стрелками, ЭДС индукции возникает в случае под номером
19. [Уд1] (О) По параллельным металлическим проводникам, расположенным в однородном магнитном поле, с постоянной скоростью перемещается перемычка. Зависимость Ei — ЭДС индукции, возникающей в цепи, правильно представлена на рисунке под номером
Тема: 250 Электромагнитные колебания и волны
V251П Электромагнитные колебания.
S251 П электромагнитные колебания – 23 задания
1. [Уд] (ВО1) В колебательном контуре зависимость заряда на пластинах конденсатора от времени описывается дифференциальным уравнением вида 
2. [Уд] (ВО1) В колебательном контуре зависимость заряда на пластинах конденсатора от времени описывается дифференциальным уравнением вида 
3. [Уд] (ВО1) В колебательном контуре зависимость заряда на пластинах конденсатора от времени описывается дифференциальным уравнением вида 
4. [Уд] (ВО1). Если частота колебаний в контуре возросла в 3 раза, а заряд конденсатора и индуктивность катушки не менялись, то энергия магнитного поля в катушке … раз(а).
1) уменьшилась в 3
2) увеличилась в 3
3) уменьшилась в 9
4) увеличилась в 9
5. [Уд] (ВО1) Максимальная энергия электрического колебательного контура 4,5 Дж. При циклической частоте свободных колебаний в контуре, равной 1·104с-1, и емкости конденсатора 4 мкФ максимальный ток через катушку индуктивности равен
6. [Уд] (ВО1) В колебательном контуре в начальный момент времени напряжение на конденсаторе максимально. Напряжение на конденсаторе станет равным нулю через долю периода 
1)
2)
3)
7. [Уд] (ВО1) В колебательном контуре в начальный момент времени напряжение на конденсаторе максимально. Сила тока станет равной нулю через долю периода 
1)
2)
3)
8. [Уд] (ВО1) Сила тока в колебательном контуре изменяется по закону 
9. [Уд] (ВО1) Если в колебательном контуре увеличить емкость конденсатора в 2 раза и заряд на нем увеличить в 2 раза, то амплитуда колебаний тока в контуре … раз(а).
1) увеличится в 2
2) увеличится в
3) уменьшится в
4) уменьшится в 2
10. [Уд] (ВО1) Если в колебательном контуре уменьшить емкость конденсатора в 2 раза, то, при одинаковом заряде конденсатора, максимальная энергия магнитного поля в катушке индуктивности … раза.
1) увеличится в 2
2) увеличится в
3) уменьшится в
4) уменьшится в 2
11. [Уд] (ВО1) Если частота колебаний в контуре возросла в 2 раза, а заряд конденсатора и индуктивность катушки не менялись, то энергия магнитного поля в катушке … раза.
1) уменьшилась в 2
2) увеличилась в 2
3) уменьшилась в 4
4) увеличилась в 4
12. [Уд] (ВО1) Время релаксации затухающих электромагнитных колебаний наибольшее в случае
1) 
2) 
3) 
4) 
13. [Уд] (ВО1) Ниже приведены уравнения затухающих электромагнитных колебаний. Логарифмический декремент затухания наибольший в случае
1) 
2)
3) 
4) 
14. [Уд] (ВО1) Уменьшение амплитуды колебаний в системе с затуханием характеризуется временем релаксации. Если при неизменном омическом сопротивлении в колебательном контуре увеличить в 2 раза индуктивность катушки, то время релаксации … раза.
1) уменьшится в 4
2) увеличится в 2
3) увеличится в 4
4) уменьшится в 2
15. [Уд] (ВО1) Уменьшение амплитуды колебаний в системе с затуханием характеризуется временем релаксации. Если при неизменной индуктивности в колебательном контуре увеличить омическое сопротивление в 2 раза катушки, то время релаксации … раза.
1) уменьшится в 4
2) увеличится в 2
3) увеличится в 4
4) уменьшится в 2
16. [Уд] (ВО1) Ниже приведены уравнения собственных незатухающих электромагнитных колебаний в четырех контурах с одинаковой емкостью. Индуктивность L контура наименьшая в случае
1) q = 10-6cos(4πt +
3) q = 10-8cos(πt +
17. [Уд] (ВО1) Ниже приведены уравнения собственных незатухающих электромагнитных колебаний в четырех контурах с одинаковой индуктивностью. Емкость C контура наибольшая в случае
1) q = 10-6cos(4πt +
3) q = 10-8cos(πt +
18. [Уд] (ВО1) Уравнение изменения тока со временем в колебательном контуре имеет вид 
19. [Уд] (ВО1) Уравнение изменения тока со временем в колебательном контуре имеет вид 
20. [Уд] (ВО1) Уравнение изменения тока со временем в колебательном контуре имеет вид 

Видео:Урок 353. Колебательный контурСкачать

Заряд на пластинах конденсатора колебательного контура изменяется с течением времени t в соответствии с уравнением q = 50 cos
Видео:Урок 8. Перезарядка конденсатора. Плотность тока смещения. Ток смещения. Физика 11 классСкачать

Ваш ответ
Видео:Свободные электромагнитные колебания. 11 класс.Скачать

решение вопроса
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Похожие вопросы
- Все категории
- экономические 43,427
- гуманитарные 33,634
- юридические 17,906
- школьный раздел 608,208
- разное 16,858
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Колебательный контур | ЕГЭ Физика | Николай НьютонСкачать

Амплитуда силы тока в контуре формула
ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ.
СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ.
Электромагнитные колебания — взаимосвязанные колебания электрического и магнитного полей.
Электромагнитные колебания появляются в различных электрических цепях. При этом колеблются величина заряда, напряжение, сила тока, напряженность электрического поля, индукция магнитного поля и другие электродинамические величины.
Свободные электромагнитные колебания возникают в электромагнитной системе после выведения ее из состояния равновесия, например, сообщением конденсатору заряда или изменением тока в участке цепи.
Это затухающие колебания, так как сообщенная системе энергия расходуется на нагревание и другие процессы.
Вынужденные электромагнитные колебания — незатухающие колебания в цепи, вызванные внешней периодически изменяющейся синусоидальной ЭДС.
Электромагнитные колебания описываются теми же законами, что и механические, хотя физическая природа этих колебаний совершенно различна.
Электрические колебания — частный случай электромагнитных, когда рассматривают колебания только электрических величин. В этом случае говорят о переменных токе, напряжении, мощности и т.д.
Колебательный контур — электрическая цепь, состоящая из последовательно соединенных конденсатора емкостью C, катушки индуктивностью L и резистора сопротивлением R.
Состояние устойчивого равновесия колебательного контура характеризуется минимальной энергией электрического поля (конденсатор не заряжен) и магнитного поля (ток через катушку отсутствует).
Величины, выражающие свойства самой системы (параметры системы): L и m, 1/C и k
величины, характеризующие состояние системы:
величины, выражающие скорость изменения состояния системы: u = x'(t) и i = q'(t) .
ХАРАКТЕРИСТИКИ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ
Можно показать, что уравнение свободных колебаний для зарядаq = q(t) конденсатора в контуре имеет вид
где q» — вторая производная заряда по времени. Величина
является циклической частотой. Такими же уравнениями описываются колебания тока, напряжения и других электрических и магнитных величин.
Одним из решений уравнения (1) является гармоническая функция
Период колебаний в контуре дается формулой (Томсона):
Величина φ = ώt + φ , стоящая под знаком синуса или косинуса, является фазой колебания.
Фаза определяет состояние колеблющейся системы в любой момент времени t.
Ток в цепи равен производной заряда по времени, его можно выразить
Чтобы нагляднее выразить сдвиг фаз, перейдем от косинуса к синусу
ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
1. Гармоническая ЭДС возникает, например, в рамке, которая вращается с постоянной угловой скоростью в однородном магнитном поле с индукцией В. Магнитный поток Ф , пронизывающий рамку с площадью S ,
где- 
По закону электромагнитной индукции Фарадея ЭДС индукции равна
где — 
Гармонически изменяющийся магнитный поток вызывает синусоидальную ЭДС индукции
где — 
2. Если к контуру подключить источник внешней гармонической ЭДС
то в нем возникнут вынужденные колебания, происходящие с циклической частотой ώ, совпадающей с частотой источника.
При этом вынужденные колебания совершают заряд q, разность потенциалов u , сила тока i и другие физические величины. Это незатухающие колебания, так как к контуру подводится энергия от источника, которая компенсирует потери. Гармонически изменяющиеся в цепи ток, напряжение и другие величины называют переменными. Они, очевидно, изменяются по величине и направлению. Токи и напряжения, изменяющиеся только по величине, называют пульсирующими.
В промышленных цепях переменного тока России принята частота 50 Гц.
Для подсчета количества теплоты Q, выделяющейся при прохождении переменного тока по проводнику с активным сопротивлением R, нельзя использовать максимальное значение мощности, так как оно достигается только в отдельные моменты времени. Необходимо использовать среднюю за период мощность — отношение суммарной энергии W, поступающей в цепь за период, к величине периода:
Поэтому количество теплоты, выделится за время Т:
Действующее значение I силы переменного тока равно силе такого постоянного тока, который за время, равное периоду T, выделяет такое же количество теплоты, что и переменный ток:
Отсюда действующее значение тока
Аналогично действующее значение напряжения
Трансформатор — устройство, увеличивающее или уменьшающее напряжение в несколько раз практически без потерь энергии.
Трансформатор состоит из стального сердечника, собранного из отдельных пластин, на котором крепятся две катушки с проволочными обмотками. Первичная обмотка подключается к источнику переменного напряжения, а к вторичной присоединяют устройства, потребляющие электроэнергию.
называют коэффициентом трансформации. Для понижающего трансформатора К > 1, для повышающего
Пример. Заряд на пластинах конденсатора колебательного контура изменяется с течением времени в соответствии с уравнением 
Из уравнения следует, что 
Зависимость силы тока от времени имеет вид:
Амплитуда силы тока.
Ответ: заряд совершает колебания с периодом 0,02 с и частотой 50 Гц, которой соответствует циклическая частота 100 рад/с, амплитуда колебаний силы тока равна 5
i=-5000 

Основным устройством, определяющим рабочую частоту любого генератора переменного тока, является колебательный контур. Колебательный контур (рис.1) состоит из катушки индуктивности L (рассмотрим идеальный случай, когда катушка не обладает омическим сопротивлением) и конденсатора C и называется замкнутым. Характеристикой катушки является индуктивность, она обозначается L и измеряется в Генри (Гн), конденсатор характеризуют емкостью C, которую измеряют в фарадах (Ф).
Пусть в начальный момент времени конденсатор заряжен так (рис.1), что на одной из его обкладок имеется заряд +Q , а на другой – заряд —Q . При этом между пластинами конденсатора образуется электрическое поле, обладающее энергией
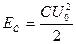
где 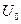
После замыкания контура конденсатор начинает разряжаться и по цепи пойдет электрический ток (рис.2), величина которого увеличивается от нуля до максимального значения 

(где 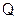

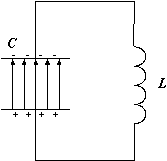 |  |
| Рис.1 | Рис.2 |
Когда конденсатор полностью разрядится 
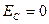


Затем сила тока начинает уменьшаться, а заряд будет накапливаться на пластинах конденсатора (рис.4). Когда сила тока уменьшится до нуля, заряд конденсатора достигнет максимального значения Q , но обкладка, прежде заряженная положительно, теперь будет заряжена отрицательно (рис. 5). Затем конденсатор вновь начинает разряжаться, причем ток в цепи потечет в противоположном направлении.
Так процесс перетекания заряда с одной обкладки конденсатора на другую через катушку индуктивности повторяется снова и снова. Говорят, что в контуре происходят электромагнитные колебания. Этот процесс связан не только с колебаниями величины заряда и напряжения на конденсаторе, силы тока в катушке, но и перекачкой энергии из электрического поля в магнитное и обратно.
 |  |
| Рис.3 | Рис.4 |
Перезарядка конденсатора до максимального напряжения 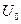
В реальных контурах имеют место следующие потери энергии:
1) тепловые потери, т.к. R ¹ 0;
2) потери в диэлектрике конденсатора;
3) гистерезисные потери в сердечнике катушке;
4) потери на излучение и др. Если пренебречь этими потерями энергии, то можно написать, что 
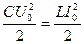
Колебания, происходящие в идеальном колебательном контуре, в котором выполняется это условие, называются свободными, или собственными, колебаниями контура.
В этом случае напряжение U (и заряд Q) на конденсаторе изменяется по гармоническому закону:
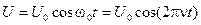
где n — собственная частота колебательного контура, w = 2pn — собственная (круговая) частота колебательного контура. Частота электромагнитных колебаний в контуре определяется как

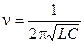
Период T – время, в течение которого совершается одно полное колебание напряжения на конденсаторе и тока в контуре, определяется формулой Томсона
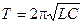
Сила тока в контуре также изменяется по гармоническому закону, но отстает от напряжения по фазе на 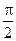
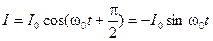
На рис.6 представлены графики изменения напряжения U на конденсаторе и тока I в катушке для идеального колебательного контура.
В реальном контуре энергия с каждым колебанием будет убывать. Амплитуды напряжения на конденсаторе и тока в контуре будут убывать, такие колебания называются затухающими. В задающих генераторах их применять нельзя, т.к. прибор будет работать в лучшем случае в импульсном режиме.
 | 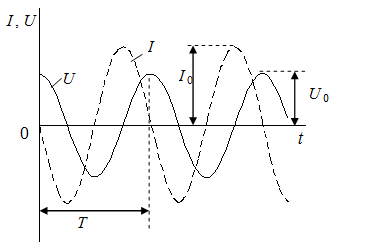 |
| Рис.5 | Рис.6 |
Для получения незатухающих колебаний необходимо компенсировать потери энергии при самых разнообразных рабочих частотах приборов, в том числе и применяемых в медицине.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 10034 — 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
07.06.2019
5 июня Что порешать по физике
30 мая Решения вчерашних ЕГЭ по математике
Колебания напряжения на конденсаторе в цепи переменного тока описываются уравнением где все величины выражены в СИ. Емкость конденсатора равна
Найдите амплитуду силы тока. (Ответ дать в амперах.)
Общий вид зависимости напряжения на конденсаторе в колебательном контуре: где
— амплитудное значение напряжения. Сравнивая с
находим, что
Значение максимального заряда на обкладках конденсатора равно
Амплитуда колебаний силы тока связана с частотой колебаний и максимальным значением заряда конденсатора соотношением
Отсюда находим
Позвольте предложить, на мой взгляд, более простой способ решения. Известно, что в цепи переменного тока, в которой есть конденсатор, выполняется зависимость Im=Um/Xc, где под током и напряжением имеются ввиду их амплитудные значения, а Хс — емкостное сопротивление конденсатора, равное Хс=1/w*C. Подставляя 2-ую формулу в первую, окончательно имеем: Im=Um*w*C. Подставляя значения величин из условия, получаем значение амплитуды силы тока, которое совпадает с вашим.
P. S. Мой способ решения кажется мне более разумным по той причине, что обе формулы даны в учебнике по физике, в отличие от последней формулы в предложенном вами способе решения.
Спасибо. Хороший вариант.
Но использованная в конце формула, конечно же, дается в школьном курсе. Ведь насколько я знаю, в этот момент в школьной физике уже начинают использовать производные. Формула следует из закона изменения заряда со временем при гармонических колебаниях и из того, что ток — это производная от заряда
📽️ Видео
Заряд разряд конденсатораСкачать

11 класс урок №10 Решение задач Электромагнитные колебанияСкачать

Зарядка конденсатора в электрической цепиСкачать

Физика 11 класс (Урок№7 - Свободные и вынужденные электромагнитные колебания. Колебательный контур.)Скачать

Физика| Колебательные процессы. Часть 1Скачать

11 класс урок №5 Свободные электромагнитные колебанияСкачать

Урок 354. Математическое описание процессов в колебательном контуреСкачать

Урок 357. Задачи на электромагнитые колебания - 1Скачать

Урок 237. Электрическая емкость. КонденсаторыСкачать

Превращение энергии при электромагнитных колебаниях | Физика 11 класс #11 | ИнфоурокСкачать

Свободные электромагнитные колебания. Практическая часть - решение задачи. 11 класс.Скачать

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫСкачать

Урок 355. Затухающие электромагнитные колебания.Скачать

Проводимость диэлектрикаСкачать