Вопрос по алгебре:
Зависимость пути от времени при прямолинейном движении точки задана уравнением: S=1/3t^3 — 2t^2 + 3
вычислить ее ускорение в момент времени t=3c
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
УСКОРЕНИЕ ЕСТЬ ВТОРАЯ ПРОИЗВОДНАЯ ПО ВРЕМЕНИ ОТ РАССТОЯНИЯ.
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.
Видео:График зависимости пути от времени.Скачать

Примеры решения задач. Пример 1.Уравнение зависимости пути s, пройденного телом, от времени t имеет вид s = 4t – 2t2 + t3 (s в м
Читайте также:
|
 |
 |
20.Какой путь пройдет человек за 10 с, двигаясь со скоростью 5,4 км/час?
21.Из пункта А в пункт В выехал автомобиль. Двигаясь на протяжении всего пути с ускорением 0,1 м/с 2 , он прибыл в пункт назначения через четверть часа. Какое расстояние между пунктами?
22.Пловец плывет против течения реки со скоростью 4 км/час. Скорость течения реки 2 км/час. Какова скорость пловца, если он плывет по течению реки?
23.Автомобиль прошел расстояние АВ со скоростью 40 км/час, а обратное ВА — со скоростью 30 км/час. Какова средняя скорость рейса?
24.Автомобиль движется по закону, представленному на графике (рис.14). Какую скорость показывает его спидометр?
25.Кинематическое уравнение движения тела имеет вид s = 5t + 0,4t 2 . Определить скорость тела через 3 с после начала движения. Какова средняя скорость тела за 3 с движения?
26.Скорость прямолинейного движения материальной точки подчиняется закону υ = 3 + 4t 2 ,м/с. Определить путь и перемещение тела за первые 2 с своего движения.
27.Ускорение прямолинейно движущейся точки изменяется по закону a = (2t 2 + 0,5),м/с 2 . Какова скорость точки через три секунды движения?
28.Вы едете на автомобиле из Красноярска до пос. Солонцы. Первую треть пути вы проехали со скоростью 50 км/час, вторую – со скоростью 70 км/час и третью – со скоростью 60 км/час. Определить среднюю скорость Вашего движения.
29.Поезд, отойдя от станции, первые 100 м пути проходит за 10 с, а следующие 300 м — за 15 с. Определить среднюю скорость движения поезда при разгоне.
30.Уравнение скорости движения тела имеет вид υ = 20 — 2t . Какой путь пройдет это тело за 3 с?
31.Для тела, движущегося прямолинейно, зависимость пройденного пути от времени имеет вид s = 2 + 3t, где t — время движения. С каким ускорением движется тело?
32.Указать графики (рис.15), описывающие равномерное (равнозамедленное) движение. Здесь υ — скорость движения; S — пройденный путь; a — ускорение; t — время.
33.При движении тела по криволинейной траектории угол между тангенциальным и нормальным ускорениями равен … .
34.В некоторой точке траектории полное ускорение движущегося объекта равно 10 м/с 2 , тангенциальное 9 м/с 2 . Определить нормальное ускорение объекта.
35.Материальная точка движется замедленно (ускоренно) по указанной траектории (рис.16) в направлении стрелки. Показать направление тангенциального (нормального, полного) ускорения в точке В.
| |
|
36.При движении тела по криволинейному пути его тангенциальное ускорение равняется 1 м/с 2 , нормальное в три раза больше. Найти полное ускорение
37.Тело движется по криволинейной траектории в направлении, указанном стрелкой. За 2 с оно переместилось из точки А в точку В. При этом его скорость менялась по закону υ = 5 + 6t 2 ,м/с. Найти путь и перемещение точки за это время.
 |
38.Вагон массой 20 т движется равнозамедленно, имея начальную скорость 36 км/час и ускорение 0,2 м/с 2 . Какое расстояние он пройдет до остановки?
39.Из пункта А в пункт В одновременно выехали два автомобиля. Первый двигался по закону приведенному на графике 1 (рис.18 а), второй — на графике 2 (рис.18 б). Какой автомобиль достигнет пункта назначения первым?
 |
40.Камень падает с высоты 100 м с начальной нулевой скоростью. Какой путь он пройдет за последние 0,2 с своего движения?
41.Камень падает с высоты 100 м с начальной нулевой скоростью. За какое время он пролетит последние 10 м своего пути?
42.Космическая ракета после вертикального старта поднялась на высоту 5 км за 10 с. С каким ускорением стартовала ракета? Сопротивлением воздуха пренебречь.
43.Свободно падающее тело в некоторой точке имело скорость 20 м/с, а в другой точке — 40 м/с. Найти расстояние между этими точками.
44.Стрела, выпущенная вертикально вверх со скоростью 40 м/с попадает в цель через 2 с. На какой высоте находилась цель? Какова была скорость стрелы при попадании ее в цель?
45.Камень, брошенный горизонтально с высоты 20 м, упал на землю на расстоянии 15 м от места броска. Определить начальную и конечную скорости камня. Показать их направления.
46.Камень бросили с начальной скоростью 10 м/с под углом 60˚ к горизонту с высоты 1 м от поверхности земли. Попадет ли он в цель, находящейся на поверхности земли расстоянии 30 м от места бросания?
47.Мяч брошен под углом 30˚ к горизонту с начальной скоростью 5 м/с. Максимальная высота подъема мяча равна … .
48.С самолета, летящего горизонтально со скоростью 800 км/час на высоте 1 км сбрасывают бомбу. На каком расстоянии от места сброса будет находиться самолет, когда бомба достигнет земли?
49.Сплошной диск вращается вокруг оси, проходящей через центр массы, в направлении стрелки. Для двух точек обода указаны вектора линейных скоростей υ1 и υ2 (рис.19). Какой из рисунков можно считать правильным?
50.В автомобильных гонках участвуют два автомобиля. У первого автомобиля диаметр колес 0,7 м, у второго — 0,5м. Колеса первого при движении вращаются с частотой 10 об/с, второго — 15 об/с. У какого автомобиля больше шансов выиграть гонку?
 |
51.Колесо диаметром 1 м движется по дороге с линейной скоростью 2 м/с. Определить угловую скорость вращения колеса.
52.По горизонтальной дороге катится обруч радиусом 30 см со скоростью 5 м/с. Каково ускорение различных точек обруча?
53.Тело движется равномерно по окружности по часовой стрелке (рис.20). Вектор ускорения при таком движении направлен по стрелке …

 |
54.Тело вращается равномерно с угловой скоростью 2 рад/с по окружности радиуса 1 м. Чему равно нормальное, тангенциальное и полное ускорения тела?
55.Автомобиль движется с постоянной по модулю скоростью по траектории, представленной на рис.21. Нормальное (или центростремительное) ускорение минимально
1) 1 2) 2 3) 3 4) Во всех точках одинаково
56.Уравнение движения материальной точки по окружности в системе СИ имеет вид φ = 3t 4 + 1. Найти угловое ускорение для момента времени 1 с.
57.Твердое тело вращается вокруг оси по закону w = 0,3t 2 + 0,1, (рад/с). Это движение является а) равномерным; б) ускоренным; в) равноускоренным; г) равнозамедленным; д) замедленным? Выбрать правильный ответ.
58. Твердое тело вращается вокруг неподвижной оси по закону φ = A + Bt + Сt 2 , где А = 10 рад; В = 4 рад /с; С = -1 рад /с 2 . Определить полное ускорение точки, находящейся на расстоянии 1 м от оси вращения в момент времени t = 4 с .
59.Вращаясь по окружности радиуса 2 м, материальная точка сделала четверть оборота за 10 с. Найти перемещение точки и пройденный ею путь.
60.Вращаясь равномерно по окружности, материальная точка сделала 2 оборота за 10 с. Определить угловую скорость вращения.
61.Вращаясь по окружности радиуса 2 м, материальная точка сделала четверть оборота за 10 с. Определить среднюю угловую скорость движения точки за это время.
62.Материальная точка начала вращаться с постоянным угловым ускорением из положения 1 и через 0,1с оказалась в положении 2 (рис.22). Найти угловые ускорение и скорость в точке 2. Указать направления тангенциального, нормального и полного ускорений, а также линейной и угловой скоростей для положения 2.
63.Угловое ускорение вращающегося маховика меняется по закону ε = 0,15t. Определить среднюю скорость маховика за первые три секунды вращения.
64.Дать характеристику движению, приведенному на графике (рис.23). Построить график зависимости ε(t) и φ(t). Считать φ0 = 0.
 | |
|
65.Воспользовавшись графиком предыдущего задания, найти среднее угловое ускорение и угловой путь вращающегося тела за 2 с движения.
66.Тело вращается равнозамедленно с начальной угловой скоростью 10 с -1 и угловым ускорением 2 с -2 . Сколько оборотов сделает тело за 5 с?
67.Вертолет и самолет летят навстречу друг другу: первый со скоростью υ , второй — 2υ относительно Земли. Какова скорость самолета относительно вертолета ?
68.Тело движется по криволинейной траектории. Пройденный путь меняется со временем по закону s = 2 + 0,5t 2 ,м. Определить нормальное, тангенциальное и полное ускорение при t = 1 с. Радиус кривизны траектории движения в этот момент времени равен 50 см. Какова средняя скорость за 1 с движения?
Дата добавления: 2015-04-15 ; просмотров: 173 ; Нарушение авторских прав
Видео:Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №19. Решение задач с помощью производной.
Перечень вопросов, рассматриваемых в теме
- механический смысл первой производной;
- механический смысл второй производных;
- скорость и ускорение.
Глоссарий по теме
Производная y’(x) функции y=f(x) – это мгновенная скорость изменения этой функции. В частности, если зависимость между пройденным путём S и временем t при прямолинейном неравномерном движении выражается уравнением S=f(t), то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени t нужно найти производную S’=f’(x) и подставить в неё соответствующее значение t, то есть v(t)=S’(t).
Производная от данной функции называется первой производной или производной первого порядка. Но производная функции также является функцией, и если она дифференцируема, то от неё, в свою очередь, можно найти производную.
Производная от производной называется второй производной или производной второго порядка и обозначается f
Производная от второй производной называется производной третьего порядка и обозначается 
Если первая производная функции – это мгновенная скорость изменения любого процесса, заданного функцией, то вторая производная – это скорость изменения скорости, то есть ускорение, то есть
Первая производная – это скорость изменения процесса, вторая производная – ускорение. (v= S’; a=v’)
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Давайте вспомним механический смысл производной:
Производная y’(x) функции y=f(x) – это мгновенная скорость изменения этой функции. В частности, если зависимость между пройденным путём S и временем t при прямолинейном неравномерном движении выражается уравнением S=f(t), то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени t нужно найти производную S’=f’(x) и подставить в неё соответствующее значение t, то есть v(t)=S'(t).
Пример 1. Точка движется прямолинейно по закону 
скорость прямолинейного движения равна производной пути по времени, то есть 
Подставив в уравнение скорости t=3 с, получим v(3)=32+4∙3-1= 20 (м/с).
Пример 2. Маховик, задерживаемый тормозом, поворачивается за t с на угол

а) угловую скорость вращения маховика в момент t = 6 с;
б) в какой момент времени маховик остановится?
Решение: а) Угловая скорость вращения маховика определяется по формуле ω=φ’. Тогда ω=(4t-0,2t 2 )=4-0,4t.
Подставляя t = 6 с, получим ω=4-0,4∙6=1,6 (рад/с).
б) В тот момент, когда маховик остановится, его скорость будет равна нулю (ω=0) . Поэтому 4-0,4t=0.. Отсюда t=10 c.
Ответ: угловая скорость маховика равна (рад/с); t=10 c.
Пример 3. Тело массой 6 кг движется прямолинейно по закону S=3t 2 +2t-5. Найти кинетическую энергию тела 
Решение: найдём скорость движения тела в любой момент времени t.
Вычислим скорость тела в момент времени t=3. v(3)=6∙3+2=20 (м/с)..
Определим кинетическую энергию тела в момент времени t=3.
Производная второго порядка. Производная n-го порядка.
Производная от данной функции называется первой производной или производной первого порядка. Но производная функции также является функцией, и если она дифференцируема, то от неё, в свою очередь, можно найти производную.
Производная от производной называется второй производной или производной второго порядка и обозначается 
Производная от второй производной называется производной третьего порядка и обозначается y»’ или f»'(x) Производную n-го порядка обозначают f (n) (x) или y (n) .
Примеры. Найдем производные четвёртого порядка для заданных функций:
f'(x)=cos 2x∙(2x)’= 2cos 2x
f 
f»'(x)= -4 cos 2x∙(2x)= -8 cos 2x
f (4) (x)= 8 sin2x∙(2x)’= 16 sin 2x
f 
f»'(x)= 27∙ 2 3x ∙ln 3 2
f (4) (x)= 81∙ 2 3x ∙ln 4 2
Механический смысл второй производной.
Если первая производная функции – это мгновенная скорость изменения любого процесса, заданного функцией, то вторая производная – это скорость изменения скорости, то есть ускорение, то есть
Итак, первая производная – это скорость изменения процесса, вторая производная – ускорение. (v= S’; a=v’)
Пример 4. Точка движется прямолинейно по закону S(t)= 3t 2 -3t+8. Найти скорость и ускорение точки в момент t=4 c.
найдём скорость точки в любой момент времени t.
Вычислим скорость в момент времени t=4 c.
Найдём ускорение точки в любой момент времени t.
a= v’= (6t-3)’=6 и a(4)= 6 (м/с 2 ) , то есть ускорение в этом случае является величиной постоянной.
Ответ: v=21(м/с); a= v’= 6 (м/с 2 ).
Пример 5. Тело массой 3 кг движется прямолинейно по закону S(t)=t 3 -3t 2 +5. Найти силу, действующую на тело в момент времени t=4 c.
Решение: сила, действующая на тело, находится по формуле F=ma.
Найдём скорость движения точки в любой момент времени t.
v=S’=(t 3 -3t 2 +5)’=3t 2 -6t.
Тогда v(4)=3∙4 2 -6∙4=24 (м/с).
Найдём ускорение: a(t)=v’=(3t 2 -6t)’=6t-6.
Тогда a(4)= 6∙4-6= 18 (м/с 2 ).
Разбор решения заданий тренировочного модуля
№ 1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Напишите производную третьего порядка для функции:
f(x)= 3cos4x-5x 3 +3x 2 -8
Решим данную задачу:
f’’’(x)=( 3cos4x-5x 3 +3x 2 -8)’’’=(((3cos4x-5x 3 +3x 2 -8)’)’)’=((-12sin4x-15x 2 +6x)’)’=(-48cos4x-30x)’=192sin4x-30.
№ 2. Тип задания: выделение цветом
Точка движется прямолинейно по закону S(t)= 3t 2 +2t-7. Найти скорость и ускорение точки в момент t=6 c.
- v=38 м/с; a=6 м/с 2
- v=38 м/с; a=5 м/с 2
- v=32 м/с; a=6 м/с 2
- v=32 м/с; a=5 м/с 2
Решим данную задачу:
Воспользуемся механическим смыслом второй производной:
v= S’(t)=( 3t 2 +2t-7)’=6t+2.
Вычислим скорость в момент времени t=6 c.
Найдём ускорение точки в любой момент времени t.
a= v’= (6t+2)’=6 и a(6)= 6 (м/с 2 ) , то есть ускорение в этом случае является величиной постоянной.
Ответ: v=38(м/с); a= v’= 6 (м/с 2 ).
- v=38 м/с; a=6 м/с 2
- v=38 м/с; a=5 м/с 2
- v=32 м/с; a=6 м/с 2
- v=32 м/с; a=5 м/с 2
🎥 Видео
Графики зависимости кинематических величин от времени при равномерном и равноускоренном движенииСкачать

ЕГЭ Физика Задание 4 #8854Скачать

Уравнение равномерного движения. Решение задач по теме.Скачать

Физика: зависимость координаты тела от времениСкачать

Примеры решения задач по теме: "Равномерно прямолинейное движение"Скачать

Математика без Ху!ни. Непрерывность функции, точки разрыва.Скачать

Импульс тела и импульс силы. Практическая часть - решение задачи. 9 класс.Скачать

Основы кинематики. Тема 10. Перемещение, координата и путь при равнопеременном движенииСкачать

Урок 29 (осн). Задачи по теме "Плотность" - 1Скачать

Урок Решение задач равномерное прямолинейное движениеСкачать

#31. Курс по решению текстовых задач: задачи на движениеСкачать

Кинематика. Решение задач на равноускоренное движениеСкачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

35. Вычисление пределов функций. Второй замечательный предел.Скачать

Разбор задач по теме: "Прямолинейное равномерное движение". Высокий уровень. Часть 1Скачать

ОБРАТНАЯ ПРОПОРЦИОНАЛЬНОСТЬ — Свойства и ГрафикСкачать

Перемещение тела при прямолинейном равноускоренном движении | Физика 9 класс #7 | ИнфоурокСкачать

Перемещение при прямолинейном равномерном движенииСкачать


 7) Полное ускорение , , т.е.
7) Полное ускорение , , т.е.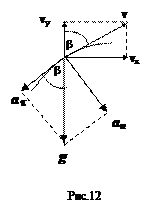 3) Скорость в указанной точке, согласно рис. 11, определится по теореме Пифагора: u = Ö ux 2 + uy 2 .Составляющую скорости uу найдем по уравнению (27) для момента времени 20с: uу = 600×0,5 – 10×20 = 100 м/с. Учтем, что uх = 600×cos30 0 =600×0,87=520 м/c, тогда u = Ö100 2 + 520 2 = 529,53 м/с
3) Скорость в указанной точке, согласно рис. 11, определится по теореме Пифагора: u = Ö ux 2 + uy 2 .Составляющую скорости uу найдем по уравнению (27) для момента времени 20с: uу = 600×0,5 – 10×20 = 100 м/с. Учтем, что uх = 600×cos30 0 =600×0,87=520 м/c, тогда u = Ö100 2 + 520 2 = 529,53 м/с







