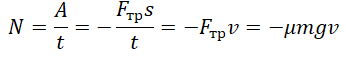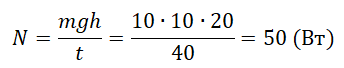Зависимость проекции силы fs от пути s выражается уравнением определите работу на втором метре пути

При решении задач по кинематике и динамики поступательного движения необходимо обратить внимание на классические законы Ньютона и границы их применения. Решая задачи, связанные с работой и энергией, повторить определения этих понятий. Необходимо понять сущность различия задач, решаемых с применением закона сохранения энергии и закона сохранения импульса. Рассматривая задачи на вращательное движение, следует обратить внимание на аналогию законов вращательного и поступательного движений, на то, что момент инерции характеризует геометрию распределения масс и не зависит от момента силы, обратить внимание на закон сохранения момента импульса.

Основные законы и формулы

Скорость мгновенная	или
Ускорение: Тангенциальное
Нормальное
Полное
Скорость угловая
Ускорение угловое
Уравнения равнопеременного вращательного движения
Связь между линейными и угловыми величинами, характеризующими движение точки по окружности
Второй закон Ньютона для поступательного движения при m = const
Количество движения тела (импульс)
Закон сохранения импульса для изолированной системы тел
Работа переменной силы на пути S
Мощность
Кинетическая энергия тела
Закон сохранения механической энергии
Момент инерции материальной точки
Момент инерции системы материальных точек
полого и сплошного цилиндра радиуса R, цилиндра радиуса R, цилиндра радиуса R
шара радиуса R
стержня длины l
Теорема Штейнера
Момент силы относительно оси вращения
Основные уравнения динамики вращательного движения
тоже при I=const
Закон сохранения момента количества движения
Кинетическая энергия вращающегося тела
Работа при вращательном движении
Зависимость массы частицы от скорости
Энергия покоя частицы
Полная энергия частицы, движущейся со скоростью v , сравнимой со скоростью света
Кинетическая энергия релятивистской частицы

Примеры решения задач

Пример 1. Тело массой 1кг под действием постоянной силы, движется прямолинейно. Зависимость пути, пройденного телом, от времени задано уравнением S=2t 2 +4t+1. Определить работу силы за 10с от начала её действия и зависимость кинетической энергии от времени.

Дано: m=1кг; S=2t 2 +4t+1

Работа, совершаемая силой

Сила, действующая на тело, по второму закону Ньютона равна:

Мгновенное ускорение определяется первой производной от скорости по времени или второй производной от пути по времени. В соответствии с этим:

Подставив (5) и (6) в уравнение (1), получим:

По этой формуле вычислим работу, совершаемую силой за 10с. С начала её действия:

Кинетическая энергия равна:

Ответ: A = 960 Дж, T = 8m (t + 1) 2

Пример 2. Сплошной цилиндр массой 0,5кг и радиусом 0,02м вращается относительно оси, совпадающей с осью цилиндра, по закону φ =12+8t-0,5t 2 . На цилиндр действует сила, касательная к поверхности. Определить эту силу и тормозящий момент.

Дано : m=0,5кг; r=0,02 м; φ =12+8t-0,5t 2

Решение: Цилиндр вращается относительно оси, совпадающей c его осью, по закону φ =12+8t-0,5t 2 . Угловое ускорение определяется как вторая производная от угла поворота по времени:

где ω — угловая скорость, равная первой производной от угла по времени: ; т.е. ω =8 — t , тогда

Момент силы относительно оси вращения: , или в скалярном виде: M=Fr· sinα , т.к. сила действует касательно к поверхности, то sinα =1 , тогда M=Fr и

Тормозящий момент можно определить из основного уравнения динамики вращательного движения:

M=Iε

(2)

где I — момент инерции цилиндра, относительно оси вращения, т.к. ось вращения совпадает с осью цилиндра, то момент инерции его равен:

Подставляем (3) в (2) имеем:

Ответ: F = -0,005 Н, M = -10 -4 Hм

Пример 3 . Определить импульс и кинетическую энергию электрона, движущегося со скоростью 0,7с ( c — скорость света в вакууме).

Дано: m 0 =9,1· 10 -31 кг; ν =0,7с; с=3· 10 8 м/с

Решение: Импульсом частицы называется произведение массы частицы на скорость её движения:

P=mν

(1)

Так как скорость электрона близка к скорости света, то необходимо учесть зависимость массы от скорости, определяемую по формуле:

где m — масса движущей частицы, m 0 — масса покоящейся частицы.

Подставляем (2) в (1) получим:

Сделаем подстановку числовых значений, входящих в формулу (3):

Кинетическая энергия T в релятивистской механике определяется как разность между полной энергией частицы E=mc 2 и её энергией покоя E 0 =m 0 c 2 , т.е. с учётом (2):

Найдём численное значение Т , подставив числовые данные в формулу (4):

Ответ: P = 2,675· 10 -22 кг· м/c, T = 3,28· 10 -14 Дж

Задачи для самостоятельного решения

1. При прямолинейном движении тела массой 1кг изменение его координаты со временем происходит по закону x=5t-10t 2 . Найти силу, действующую на тело.

2. Тело массой 3кг движется с ускорением, изменяющимся по закону a=10t-10 , v 0 =0. Определить силу, действующую на тело через 3 с после начала её действия и скорость тела в конце третьей секунды.

3. Тело движется под действием постоянной силы 15Н . Зависимость координаты от времени имеет вид: x=10-5t+2t 2 . Найти массу тела.

4. Найти зависимость скорости от времени и силу, действующую на тело массой 0,1кг в конце третьей секунды, если координата со временем изменяется по закону x=2t-t 2 +3t 3 .

5. Тело массой 2кг движется со скоростью, зависимость которой от времени выражается уравнением v=2,5t 2 +10t . Определить путь, пройденный телом за 5с и силу, действующую на тело в конце пятой секунды.

6. Сплошной шарик массой 400г и радиусом 5см вращается вокруг своей оси, проходящей через его центр. Закон вращения шара имеет вид: φ =4+2t-2t 2 . Определить вращающий момент.

7. Стержень массой 1кг и длиной 1м вращается вокруг своей оси, проходящей через один из его концов, по закону φ =2+t+t 2 . Определить момент силы, действующий на другой его конец.

8. Сплошной диск массой 0,2кг вращается вокруг своей оси, проходящей через центр его масс, под действием момента сил 0,8· 10 -2 Нм . Закон вращения имеет вид: φ =5-t+2t 2 . Определить радиус диска.

9. Полый цилиндр вращается относительно оси, совпадающей с осью цилиндра. Закон вращения имеет вид: φ =10-5t+0,5t 2 . Определить момент инерции и массу цилиндра, если его радиус 0,05м . Момент силы относительно оси вращения, действующий на цилиндр, равен 0,75Нм .

10. Шар и сплошной цилиндр имеют одинаковую массу 5кг и катятся с одинаковой скоростью 10м/с . Найти кинетические энергии этих тел.

11. Масса движущегося протона 2,25· 10 -27 кг. Найти скорость и кинетическую энергию протона.

12. Электрон прошёл ускоряющую разность потенциала 100 МВ . Во сколько раз его релятивистская масса больше массы покоя. Вычислить его полную и кинетическую энергии.

13. Определить скорость протона, если его релятивистская масса в три раза больше массы покоя. Вычислить кинетическую и полную энергии.

14. Вычислить скорость, полную и кинетическую энергии протона в тот момент, когда его масса равна массе α — частицы ( m 0α =6,44· 10 -27 кг ).

15. Найти импульс, полную и кинетическую энергии электрона, движущегося со скоростью, равной 0,9с .

16. Протон прошёл ускоряющую разность потенциалов, после чего его масса стала равна половине массы α — частицы ( m 0α =6,44· 10 -27 кг ). Определить разность потенциалов.

17. С какой скоростью движется электрон, если его кинетическая энергия равна 1,78МэВ ? Определить импульс электрона.

18. Кинетическая энергия частицы оказалась равной её энергии покоя. Какова скорость этой частицы?

19. При какой скорости масса любой частицы вещества в 5 раз больше его массы покоя?

20. Во сколько раз масса движущегося электрона, обладающего кинетической энергией 1МэВ больше его массы покоя?

21. Сплошной цилиндр массой 10кг катится без скольжения с постоянной скоростью 10м/с . Определить кинетическую энергию цилиндра и время его остановки, если на него подействует сила 50Н .

22. Стержень массой 2кг и длиной 1м может вращаться вокруг оси, проходящей через его середину перпендикулярно стержню. В конец стержня попадает пуля массой 10г , летящая перпендикулярно оси и стержню со скоростью 500м/с . Определить угловую скорость, с которой начнет вращаться стержень, если пуля застрянет в нем.

23. Сплошной шар, скатывается по наклонной плоскости, длина которой 10м и угол наклона 30°. Определить скорость шара в конце наклонной плоскости.

24. Полый цилиндр массой 2кг катится по горизонтальной поверхности со скоростью 20м/с . Определить силу, которую необходимо приложить к цилиндру, чтобы остановить его на пути 1,6м .

25. Маховик, имеющий форму диска массой 30кг и радиусом 10см , был раскручен до частоты 300 мин -1 . Под действием силы трения диск остановился через 20с . Найти момент силы трения, считая его постоянным.

26. Автомобиль массой 5т движется равнозамедленно, при этом в течении десяти секунд его скорость уменьшается от 72км/час до 54км/час . Найти силу торможения.

27. Тело массой 1кг под действием постоянной силы движется прямолинейно. Зависимость пути, пройденного телом, от времени выражается уравнением S=t 2 +2t+2 . Определить работу силы за 5с после начала её действия.

28. В каком случае двигатель автомобиля совершит большую работу (во сколько раз): разгон с места до скорости 36км/час или увеличение скорости от 36км/час до 72км/час ? Силу сопротивления и время движения в обоих случаях считать одинаковыми.

29. Тело массой 2кг под действием постоянной силы движется и зависимость пути, пройденного телом, от времени выражается уравнением: S=t 2 +2t+2 . Найти зависимость кинетической энергии от времени и её значение в конце второй секунды.

30. Найти силу тяги, развиваемую мотором автомобиля, движущегося в гору с ускорением 1м/с 2 . Уклон горы равен 1м на каждые 25м пути. Масса автомобиля 9,8· 10 2 кг . Коэффициент трения равен 0,1.

Качественные задачи

31. Зависимость пройденного пути от времени s(t) для двух материальных точек, движущихся прямолинейно, представлена кривыми 1 и 2 (рис.1). Спрашивается, какая кривая соответствует возрастанию скорости точки, а какая — убывающей скорости?

32. Поперек реки, скорость течения которой , плывет лодка. Скорость лодки относительно воды направлена под углом к линии, перпендикулярной течению реки. Под каким углом относительно той же линии движется лодка?

33. Материальная точка движется по спирали. При этом нормальное ускорение постоянно: аn=сonst. Как изменяются линейная и угловая скорости?

34. В какую сторону вдоль оси вращения Земли направлен вектор угловой скорости при суточном её вращении?

35. Вектор угловой скорости диска направлен на восток при вращении относительно горизонтальной оси. Указать направление линейной скорости точек обода диска?

36. Пуля массой m , летящая горизонтально, попадает в подвешенный на шнуре предмет массы М . При этом возможны три случая: 1) пуля застревает в предмете, 2) пуля пробивает предмет и сохраняет только часть своей энергии, 3) пуля после удара отскакивает от предмета. В каком из этих случаев предмет поднимется на большую высоту и в каком — на наименьшую?

37. Зависит ли скорость тела у основания наклонной плоскости от угла, который она составляет с горизонтом при наличии трения или без него при скатывании этого тела без начальной скорости?

38. Два шара одинаковой массы сталкиваются (абсолютно упругий удар), испытывая нецентральный удар. Доказать, что угол между направлениями скоростей шаров после удара составляет угол 90 0 ?

39. Зависимость потенциальной энергии тел от их положения изображается параболой W p =bx 2 . По какому закону изменяются силы, действующие на эти тела?

40. У вертолетов, кроме несущего винта, на хвостовой части имеется дополнительный винт. Поясните, зачем нужен этот винт?

41. Как можно найти емкость сосуда, используя только весы и набор гирь?

42. Цилиндрический стакан до краёв наполнен жидкостью. Каким образом содержимое стакана разделить на две равные части, имея меньший сосуд произвольной формы?

43. Определите диаметр мяча линейкой.

44. Автомобиль спускается с горы с выключенным двигателем. За счет какой энергии движется автомобиль при этом?

45. Два шара разной массы, имеющие одинаковые кинетические энергии летят навстречу друг другу. В какую сторону они полетят после абсолютно неупругого столкновения? Удар лобовой.

46. Можно ли по графику зависимости пути от времени найти среднюю скорость движения м.т. по траектории?

47. Изменится ли ускорение машины, если она совершает крутой поворот с постоянной скоростью, по сравнению с ее ускорением на закруглении большего радиуса?

48. Чем отличается кинетическая энергия вращательного движения тела от кинетической энергии его поступательного движения?

49. Почему контактный провод трамвайной линии всегда идет зигзагом, а не параллельно рельсам?

50. Под каким углом разлетятся два одинаковых упругих шара после центрального удара, если один из них до удара покоился?

Контрольные вопросы

1. Дайте характеристику основных физических понятий кинематики.

2. Назовите четыре типа взаимодействий современной физики.

3. Чем характеризуется положение материальной точки в пространстве?

4. В чем различие вектора перемещения и расстояния, пройденного м.т. по траектории при ее движении?

5. Физический смысл мгновенной скорости. Как направлен вектор мгновенной скорости?

6. Физический смысл мгновенного ускорения. Как направлен вектор мгновенного ускорения?

7. Физический смысл нормального, тангенциального, полного ускорения. Как направлено каждое из них?

8. В чем заключается физический смысл угловой скорости?

9. Как связаны линейная и угловая скорости в векторном виде?

10. Что такое сила?

11. Что такое импульс м.т. (тела)?

12. Сформулируйте закон всемирного тяготения и его границы применения.

13. Преобразования Галилея и принцип относительности.

14. Принцип независимости действия сил.

15. Что такое энергия?

16. Что такое кинетическая энергия и как она связана с работой?

17. Сформулируйте закон сохранения механической энергии.

18. Cформулируйте теорему Штейнера-Гюйгенса.

19. Сформулируйте закон сохранения вектора момента импульса.

20. Запишите формулу работы тел при вращательном движении.

© ФГОУ ВПО Красноярский государственный аграрный университет, 2015

Задания к итоговому экзамену по физике

Билет 9

1. Зависимость проекции силы (Fs) от пути (S) дана на графике. Определить работу на первых четырёх метрах.

1. 4 Дж; 2. 8 Дж; 3. 16 Дж; 4. 18 Дж.

2. До какой температуры нужно прогреть воздух, взятый при 15 ºС, чтобы его объём удвоился, если давление останется постоянным?

1. 583 К; 2. 303 К; 3. 576 К; 4. 313 К.

3. Какое уравнение выражает первое начало термодинамики для изобарического процесса?

1.Q=ΔU+A; 2.Q=ΔU; 3.Q=A; 4.ΔU=-A; 5.Q=0.

4.На каком рисунке в графическом решении допущена ошибка?

5.Проволоку разрезали пополам и сложили вдвое. Как изменится ее сопротивление? Укажите верный ответ.

1. увеличится в 2 раза 2. увеличится в 4 раза

3. уменьшится в 2 раза 4. уменьшится в 4 раза

6. Какая волна называется поперечной? Найдите правильный ответ. Волна называется поперечной, если частицы среды колеблются:

1…вдоль направления колебания;

2…перпендикулярно направлению распространения колебания;

3…во всевозможных направлениях;

4… вдоль направления распространения колебания и перпендикулярно направлению распространения колебания.

7.Угол преломления луча в жидкости равен 36 0 . Определить показатель преломления этой жидкости, если отраженный от ее поверхности луч при этом угле падения максимально поляризован.

1. 1.08; 2. 1.28; 3. 1.38; 4. 1.48.

8. Двояковыпуклая линза с показателем преломления n=1,5 имеет одинаковые радиусы кривизны поверхностей, равные 10 см. Определить фокусное расстояние линзы.

1. 5см; 2. 10см; 3. 0.1см; 4. 50 см.

9. По формуле Де Бройля λ=һ/ mυ. Если длина волны частиц одинакова, то наибольшией скоростью будут обладать:

1. протоны; 2. электроны; 3. нейтроны; 4. α -частицы

10. В состав атомного ядра входят:

1. протоны; 2. нейтроны; 3. протоны и нейтроны; 4. электроны и нейтроны.

Выберите правильный ответ.

Задания к итоговому экзамену по физике

Билет 8

V 2 1

1. На рисунке представлена зависимость

скорости от времени. Какой график

соответствует равнозамедленному движению?

2. Как запишется первое начало термодинамики для изотермического процесса?

1. ΔQ=ΔU+A; 2. ΔQ=ΔU; 3. ΔQ=A; 4.ΔU= — A; 5.Q=0.

3. Необходимо изготовить плосковыпуклую линзу с оптической силой Д = 4 дптр. Определить радиус кривизны выпуклой поверхности линзы, если показатель преломления материала линзы 1,6

1. 25см; 2. 6,6см; 3. 4см; 4. 15 см

4. Найти длину волны излучения, фотоны которого имеют частоту 5∙10 14 Гц.

1. 60 нм; 2. 1,7 нм; 3. 600 нм; 4. 170 нм.

5.Какое утверждение неверно? Сопротивление проводника.

1. равно отношению напряжения к силе тока;

2. зависит от напряжения и силы тока;

3. зависит от температуры;

4. зависит от его размеров.

6.Как изменится скорость распространения света при переходе из вакуума в прозрачную среду с абсолютным показателем преломления n =2?

1. увеличится в 2 раза; 2. остается неизменным;

3. уменьшится в 2 раза; 4. изменение зависит от угла падения.

7. При температуре 27 ºС давление газа в баллоне 2 ∙ 10 5 Па. При какой температуре его давление будет равно 3 ∙ 10 5 Па?

1. 210 К; 2. 450 К; 3. 520 К; 4. 150 К.

8. Определить КПД идеальной тепловой машины, если известно, что за один цикл произведена работа 4 кДж и холодильнику передано энергии 16 кДж.

1. 16%; 2. 20%; 3. 25%; 4. 40%.

9. Укажите значение кинетической энергии диска массой m, катящегося по горизонтальной поверхности со скоростью

1. Т=mυ 2 ; 2. Т=0,7×mυ 2 ; 3. Т = ¾ ×mυ 2 ; 4. Т =½×mυ 2.

10.При бомбардировке ядер изотопа азота нейтронами образуется изотоп бора

. Какая ещё частица образуется в этой ядерной реакции?

1. Протон. 2. α – частица. 3. Нейтрон. 4. 2 нейтрона.

Механическая работа и мощность

теория по физике 🧲 законы сохранения

Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:

В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.

Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).

Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:

Важно!

Механическая работа совершается, если:

1. На тело действует сила.
2. Под действием этой силы тело перемещается.
3. Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).

Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.

Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.

Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:

Работа различных сил

Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.

Модуль силы тяжести: F_тяж = mg

Работа силы тяжести: A = mgs cosα

Модуль силы трения скольжения: F_тр = μN = μmg

Работа силы трения скольжения: A = μmgs cosα

Модуль силы упругости: F_упр = kx

Работа силы упругости:

Работа силы тяжести

Работа силы трения скольжения

Работа силы упругости

Работа силы упругости

Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):

Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:

Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:

Работы силы трения покоя

Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.

Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.

A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)

Знак работы силы

Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:

1. Если α = 0 о , то cosα = 1.
2. Если 0 о o , то cosα > 0.
3. Если α = 90 о , то cosα = 0.
4. Если 90 о o , то cosα о , то cosα = –1.

Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180 о ). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0 о ). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.

Геометрический смысл работы

Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.

Мощность

Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:

Рассмотрим частные случаи определения мощности в таблице.

Мощность при равномерном прямолинейном движении тела

Работа при равномерном прямолинейном движении определяется формулой:

F_т — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна:

Мощность при равномерном подъеме груза

Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому:

Мгновенная мощность при неравномерном движении

Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость:

Мощность силы трения при равномерном движении по горизонтали

Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180 о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения:

Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?

Коэффициент полезного действия

Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.

• Работа затраченная — полная работа силы, совершенной над телом (или телом).
• Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
• Коэффициент полезного действия(КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.

КПД определяется формулой:

Работа может определяться как произведение мощности на время, в течение которого совершалась работа:

Поэтому формулу для вычисления КПД можно записать в следующем виде:

Частые случаи определения КПД рассмотрим в таблице ниже:

Устройство

Работа полезная и полная

Неподвижный блок, рычагНаклонная плоскость

l — совершенный путь (длина наклонной плоскости).

Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.

В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:

Тесты на экзамен по физике (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5

А) ;

48. Колесо, вращаясь равноускоренно при N=10об достигает угловой скорости =20рад/с. Найти угловое ускорение колеса:

С) ;

49. Каким соотношением можно определить мгновенное ускорение вращательного движения:

А) ;

50. Точка движется равномерно по окружности со скоростью 4 м/с. Чему равен радиус окружности (м), если ускорение точки равно 2 м/с2.

51. Как изменится нормальное ускорение точки, если она будет двигаться равномерно по окружности вдвое большего радиуса с той же скоростью.

Е) Уменьшится в 2 раза.

52. Какой угол составляют векторы угловой скорости и углового ускорения при замедлении вращения тела вокруг закрепленной оси.

53. Какой угол составляют векторы угловой скорости и углового ускорения при увеличении угловой скорости.

54. Первая космическая скорость для Марса (R=3400 км, g=3,6 м/с2) составит (примерно):

55. Первая космическая скорость для Венеры (R=6000 км, g= 8,4 м/с2) составит (примерно):

56. Первая космическая скорость :

А) ;

57. Вторая космическая скорость :

А) ;

58. На гироскоп с моментом импульса 6 кг. м2/с действует момент силы, равный 0,9 Н. м. При этих условиях угловая скорость прецессии составит:

59. Во сколько раз вес тела в лифте, движущемся с ускорением 5 м/с2, направленным вверх больше, чем вес тела в лифте, движущемся с ускорением 5 м/с2 , направленным вниз:

60. Масса тела есть:

А) Мера инертности тела;

61. Что такое сила:

С) Мера взаимодействия тел;

62. Какое из приведенных выражений является основным уравнением динамики поступательного движения:

А) ;

63. Две силы и, приложены к одной точке тела. Угол между векторами и равен . Определить модуль равнодействующей этих сил:

64. Две силы и, приложены к одной точке тела. Угол между векторами и равен 0. Определить модуль равнодействующей этих сил:

65. Две силы и, приложены к одной точке тела. Угол между векторами и равен . Определить модуль равнодействующей этих сил:

66. Снаряд массы m, летящий вдоль оси Х со скоростью V, разрывается на два одинаковых осколка. Один из них продолжает двигаться в том же направлении со скоростью 2V. Чему равен импульс второго осколка:

67. Скорость легкового автомобиля в 2 раза больше скорости грузового, а масса грузового автомобиля в 2 раза больше массы легкового. Сравните значения импульсов легкового рЛ и грузового рг автомобилей:

68. Поезд массой m= 500т. При торможении двигается равнозамедленно. В течене 1 минуты его скорость уменьшается от =40 км/ч до =28 км/ч. Найти силу торможения F:

С) Н;

69. Какая из приведенных формул выражает силу сопротивления среды при медленном движении тела в вязкой среде.

A) ;

70. Под действием силы 80 Н пружина удлинилась на 2 см. Чему равна жесткость пружины.

71. Величина момента силы имеет размерность:

72. В каких единицах измеряется момент инерции:

73. Величина момента импульса имеет размерность:

74. Величина импульса имеет размерность:

75. Какая из векторных физических величин всегда совпадает по направлению с вектором силы в классической механике.

76. Первое тело массой 2 кг движется со скоростью 6 м/с, второе неподвижно. После столкновения оба тела движутся со скоростью 2 м/с. Найти массу (кг) второго тела.

77. Тело массой 3 кг, двигаясь со скоростью 6 м/с, догоняет другое тело, движущееся в том же направлении со скоростью 2 м/с. После столкновения оба тела движутся вместе со скоростью 4,4 м/с. Найти массу второго тела.

78. Тело массой 3 кг, двигаясь со скоростью 6 м/с сталкивается с другим телом, движущимся в противоположном направлении. После удара оба тела остановились. Найти начальную скорость (м/с) второго тела, если его масса — 2 кг.

79. Какие из сил: 1) гравитации; 2) упругие; 3) трения являются консервативными.

80. Какие из сил: 1) гравитации; 2) упругие; 3) трения являются диссипативными:

81. С наклонной плоскости высотой 5м соскользнуло тело массой 3 кг. Какой импульс (Н. с) приобрело тело: Трением пренебречь, g=10 м/с2.

82. Найти начальную скорость (м/с) шайбы, если она остановилась, пройдя по льду расстояние 25 м: (g=10 м/с2, коэффициент трения скольжения μ=0,2).

83. Уравнение движения материальной точки х=5-8t+4t2. Чему равен импульс тела массой 2 кг в момент времени 2 с:

D) 16H;

84. Вес тела :

А) Равен силе тяжести, если тело покоится или движется равномерно прямолинейно;

85. Камень бросили вертикально вниз с высокой башни с начальной скоростью 3 м/с. Какой путь (м) пройдет камень, когда его скорость станет 7 м/с: Трением пренебречь, g=10 м/с2.

86. Камень бросили вертикально вверх со скоростью 12 м/с. На какой высоте (м) скорость камня равна 2 м/с: Трением пренебречь g=10 м/с2.

87. Камень бросили в горизонтальном направлении с башни высотой 10м со скоростью 2м/с. На какой высоте (м) скорость камня достигнет 8м/с:

88. Какая формула пригодная для вычисления работы переменной силы на пути S (Fs –проекция силы на направления движения):

А) ;

89. На рисунке приведен график зависимости проекции Fs силы, действующей на тело, от пути. Чему равна работа силы на первых 30м:

90. Как изменится запас потенциальной энергии упруго деформированного тела при уменьшении его деформации в 2 раза:

Е) Уменьшится в 4 раза.

91. На тело, движущееся прямолинейно, действует переменная сила. Найдите работу этой силы (Дж) из графика на отрезке (3; 4):

92. На тело, движущееся прямолинейно, действует переменная сила. Найдите работу этой силы (Дж) из графика на отрезке (1; 3):

93. На тело, движущееся прямолинейно, действует переменная сила. Найдите работу этой силы (Дж) из графика на отрезке (0; 3):

94. Момент импульса вращающегося тела относительно оси определяется выражением:

А) ;

95. Укажите выражение, определяющее момент импульса материальной точки относительно некоторой неподвижной точки:

А) ;

96. Какая из приведенных формул выражает основной закон динамики вращательного движения:

С) ;

97. Какая из приведенных формул выражает момент импульса тела при вращательном движении:

D) ;

98. Тонкий однородный стержень длиной и массой m=0,4 кг вращается с угловым ускорением =3 рад/с около оси, проходящей перпендикулярно стержню через его середину. Чему равен вращающий момент:

🎥 Видео