Затухающие колебания дифференциальное уравнение затухающих колебаний его решение и анализ (2 видео)

Затухающие колебания дифференциальное уравнение затухающих колебаний его решение и анализ

§6 Затухающие колебания

Декремент затухания. Логарифмический декремент затухания.

Добротность

Свободные колебания технических систем в реальных условиях протекают, когда на них действуют силы сопротивления. Действие этих сил приводит к уменьшению амплитуды колеблющейся величины.

Колебания, амплитуда которых из-за потерь энергии реальной колебательной системы уменьшается с течением времени, называются затухающими.

Наиболее часто встречается случаи, когда сила сопротивления пропорциональна скорости движения

где r — коэффициент сопротивления среды. Знак минус показывает, что F_C направлена в сторону противоположную скорости.

Запишем уравнение колебаний в точке, колеблющийся в среде, коэффициент сопротивлений которой r . По второму закону Ньютона

где β — коэффициент затухания. Этот коэффициент характеризует скорость затухания колебаний, При наличии сил сопротивления энергия колеблющейся системы будет постепенно убывать, колебания будут затухать.

— дифференциальное уравнение затухающих колебаний.

— у равнение затухающих колебаний.

ω – частота затухающих колебаний:

Период затухающих колебаний:

Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно говорить, когда β мало.

Если затухания выражены слабо (β→0), то . Затухающие колебания можно

рассматривать как гармонические колебания, амплитуда которых меняется по экспоненциальному закону

В уравнении (1) А₀ и φ₀ — произвольные константы, зависящие от выбора момента времени, начиная е которого мы рассматриваем колебания

Рассмотрим колебание в течение, некоторого времени τ, за которое амплитуда уменьшится в е раз

τ — время релаксации.

Коэффициент затихания β обратно пропорционален времени, в течение которого амплитуда уменьшается в е раз. Однако коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент (по-русски: уменьшение) затухания D , который равен отношению амплитуд, отстоящих по времени на период:

Логарифмический декремент затухания равен логарифму D :

Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний уменьшилась в е раз. Логарифмический декремент затухания — постоянная для данной системы величина.

Еще одной характеристикой колебательной система является добротность Q .

Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ.

Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии.

Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.

Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим.

§7 Вынужденные колебания.

Резонанс

В целом ряде случаев возникает необходимость создания систем, совершающих незатухающие колебания. Получить незатухающие колебания в системе можно, если компенсировать потери энергии, воздействуя на систему периодически изменяющейся силой.

Запишем выражение для уравнения движения материальной точки, совершающей гармоническое колебательное движение под действием вынуждающей силы.

По второму закону Ньютона:

(1)

— дифференциальное уравнение вынужденных колебаний.

Это дифференциальное уравнение является линейным неоднородным.

Его решение равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения:

Найдем частное решение неоднородного уравнения. Для этого перепишем уравнение (1) в следующем виде:

(2)

Частное решение этого уравнения будем искать в виде:

т.к. выполняется для любого t , то должно выполняться равенство γ = ω , следовательно,

Это комплексное число удобно представить в виде

где А определяется по формуле (3 ниже), а φ — по формуле (4), следовательно, решение (2),в комплексной форме имеет вид

Его вещественная часть, являвшаяся решением уравнения (1) равна:

(3)

(4)

Слагаемое Х_о.о. играет существенную роль только в начальной стадии при установлении колебаний до тех пор, пока амплитуда вынужденных колебаний не достигнет значения определяемого равенством (3). В установившемся режиме вынужденные колебания происходят с частотой ω и являются гармоническими. Амплитуда (3) и фаза (4) вынужденных колебаний зависят от частоты вынуждающей силы. При определенной частоте вынуждающей силы амплитуда может достигнуть очень больших значений. Резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте механической системы, называется резонансом.

Частота ω вынуждающей силы, при которой наблюдается резонанс, называется резонансной. Для того чтобы найти значение ω_рез, необходимо найти условие максимума амплитуды. Для этого нужно определить условие минимума знаменателя в (3) (т.е. исследовать (3) на экстремум).

Зависимость амплитуды колеблющейся величины от частоты вынуждающей силы называется резонансной кривой. Резонансная кривая будет тем выше, чем меньше коэффициент затухания β и с уменьшением β, максимум резонансных кривых смешается вправо. Если β = 0, то

При ω→0 все кривые приходят к значению — статическое отклонение.

Параметрический резонанс возникает в том случае, когда периодическое изменение одного из параметров система приводит к резкому увеличению амплитуды колеблющейся системы. Например, кабины, делающие «солнышко» за счет изменения положения центра тяжести система.(То же в «лодочках».) См. §61 .т. 1 Савельев И.В.

Содержание

Дифференциальное уравнение затухающих колебаний и его решение
Затухающие колебания
4.2 Затухающие колебания
4.2.1 Дифференциальное уравнение затухающих колебаний
4.2.2 Параметры затухающих колебаний
4.4 Автоколебания
4.5 Переменный ток
4.5.1 Вынужденные электромагнитные колебания. Закон Ома для переменного тока.
4.5.2 Мощность, выделяемая в цепи переменного тока
💥 Видео

Видео:Затухающие колебания. Вынужденные колебания | Физика 9 класс #26 | ИнфоурокСкачать

Дифференциальное уравнение затухающих колебаний и его решение

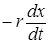
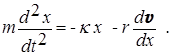
В реальных системах всегда существуют некоторые силы сопротивления, препятствующие развитию колебательных процессов. Для установления характера колебательного движения в этом случае будем считать, что наряду с упругой или квазиупругой силой F_y в системе действует сила трения, пропорциональная скорости и направленная противоположно ей: F_тр = . Тогда учет влияния этих двух сил на характер движения приводит к следующему дифференциальному уравнению:

(8)

Разделив левую и правую части уравнения (8) на m , обозначив r/m = 2b и сохранив обозначение к/m = w₀ 2 , приведем это уравнение к виду:

(9)

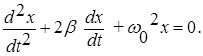
Решение этого уравнения имеет вид:

(10)

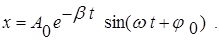
Формула (10) представляет собой смещение при затухающем колебании как функцию времени и параметров системы b и w. Коэффициент b = r/2m имеет смысл коэффициента затухания. Из формулы (10) видно, что в затухающих колебаниях амплитуда уменьшается со временем. Причем, колебания затухают тем быстрее, чем больше коэффициент затухания b. По сравнению с гармоническими колебаниями уменьшается также и циклическая частота колебаний. Это уменьшение зависит от коэффициента затухания. Оказывается, что

(11)

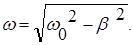
Колебательный процесс может происходить лишь при условии:
(w₀ 2 — b 2 )>0, когда частота w в формуле (11) является действительной величиной . Если же затухание в системе слишком велико (w₀

Дата добавления: 2016-01-20 ; просмотров: 2004 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:70. Затухающие колебанияСкачать

Затухающие колебания

4.2 Затухающие колебания

4.2.1 Дифференциальное уравнение затухающих колебаний

Если кроме возвращающей силы на систему действует ещё и сила сопротивления (например, сила трения в механической системе или сопротивление проводника в контуре), то энергия колебательной системы будет расходоваться на преодоление этого сопротивления. Вследствие этого амплитуда колебаний будет уменьшаться и колебания будут затухать. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических системах, а также омических потерь и излучения электромагнитной энергии в электрических колебательных системах.

Рассмотрим затухание на примере пружинного маятника с коэффициентом упругости k, массой m, колеблющегося в среде, например, в жидкости, с коэффициентом сопротивления r. Предположим, что колебания малы и что маятник испытывает вязкое трение. В этом случае можно считать, что сила сопротивления пропорциональна скорости:

Знак минус указывает на противоположные направления силы трения и скорости. Закон движения маятника при данных условиях будет иметь вид:

Преобразуем это выражение:

(51)

Обозначим: w02 = = d, где w0 — циклическая частота собственных колебаний пружинного маятника при отсутствии сил сопротивления, d — коэффициент затухания. Дифференциальное уравнение затухающих колебаний маятника примет вид:

(52)

Получили однородное дифференциальное уравнение, второго порядка, описывающее малые затухающие колебания в системе с вязким трением. Его решение имеет вид:

где ω — частота затухающих колебаний:

w = . (54)

Уравнение (52) справедливо для любой системы, как механической, так и немеханической, например, для электромагнитного контура. Действительно, для колебательного контура с сопротивлением R второе правило Кирхгофа имеет вид уравнения (29), которое после преобразований принимает вид:

Из сравнения с уравнением (52) следует:

Таким образом, дифференциальное уравнение затухающих колебаний

любой линейной системы в общем виде задается уравнением:

+ 2d+w02S = 0. (55)

где S — колеблющаяся величина, описывающая тот или иной физический процесс, d = const – коэффициент затухания, w0 — собственная циклическая частота колебательной системы, т. е. частота свободных незатухающих колебаний той же колебательной системы (при отсутствии потерь энергии) Решение уравнения (55) имеет вид:

амплитуда затухающих колебаний; A0 — начальная амплитуда.

Таким образом, затухающие колебания описываются функцией с экспоненциально убывающей амплитудой, т. е. затухающие колебания не являются гармоническими.

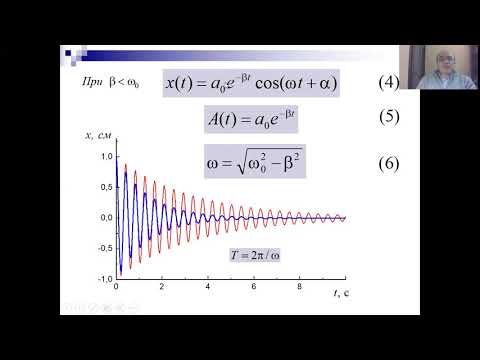
Зависимость (56) показана на рисунке 10 сплошной линией, а зависимость (57) — штриховыми линиями. Если пропорциональность силы трения и скорости не выполняются, то и закон убывания амплитуды будет другим. Например при сухом трении Fтр ≠ ƒ(t), Fтр = const и амплитуда убывает согласно геометрической прогрессии. Во многих измерительных приборах наряду с вязким трением (наличие смазки) присутствует и сухое трение (напр. в подшипниках). Пока амплитуды колебаний велики, в затухании доминирует вязкое трение. При малых амплитудах преобладает влияние сухого трения.

4.2.2 Параметры затухающих колебаний

1) Период затухающих колебаний:

Т = (58)

При δ β2 , согласно формуле (58) Т → 2π/ ωo. Такой режим затухания называют периодическим или колебательным (рисунок 10). В этом случае для характеристики процессов в системе можно использовать параметры гармонических колебаний.

2) При ωo2 ≈ β2 наступает критический режим колебаний. В формуле (58) ω → 0, Т → ∞. Наличие большого затухания в системе приводит к большим потерям энергии, поэтому, перейдя положение равновесия, система не в состоянии отойти от него на сколь-нибудь заметное расстояние и возвращается к равновесию (рисунок 11). Условие наблюдения критического режима можно получить из соотношений:

а) для механической системы

rk = 2 (67)

в) по аналоги для электрической системы

. (68)

3) При ωo2 wо2) выражение для резонансной частоты становится мнимым. Это означает, что при этих условиях резонанс не наблюдается — с увеличением частоты амплитуда вынужденных колебаний монотонно убывает. Изображенная на рисунке 13 совокупность графиков функции (79), соответствующих различным значениям параметра d, называется резонансными кривыми.

По поводу резонансных кривых можно сделать еще следующие замечания. При стремлении wо к нулю все кривые приходят к одному и тому же, отличному от нуля, предельному значению, равному fо/wо2, т. е. Fo/k. Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы величины Fo. При w → ∞ все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместиться из положения равновесия. Наконец, отметим, что чем меньше d, тем сильнее изменяется с частотой амплитуда вблизи резонанса, тем «острее» получается максимум. Из формулы (79) вытекает, что при малом затухании (т. е. при d > w 0, tgj = -2δ/ω и сдвиг фаз становится равным p. Зависимость j от w при разных значениях d показана графически на рисунке 14.

При слабом затухании wрез» w0, и значение j при резонансе можно считать равным p/2.Сдвиг фаз на p/2 при резонансе означает, что вынуждающая сила опережает смещение на Т/4. При этом условии работа вынуждающей силы всегда положительна и приток энергии к колебательной системе максимален.

С явлением резонанса приходится считаться при конструировании машин и различного рода сооружений. Собственная частота колебаний этих устройств ни в коем случае не должна быть близка к частоте возможных внешних воздействий. В противном случае возникают вибрации, которые могут вызвать катастрофу. Известны случаи, когда обрушивались мосты при прохождении по ним марширующих колонн солдат. Это происходило потому, что собственная частота колебаний моста оказывалась близкой к частоте, с которой шагала колонна.

Вместе с тем явление резонанса часто оказывается весьма полезным, особенно в акустике, радиотехнике и т. д.

4.4 Автоколебания

Огромный интерес для техники представляет возможность поддерживать колебания незатухающими. Для этого необходимо восполнять потери энергии реальной колебательной системы. Особенно важны и широко применимы так называемые автоколебания — незатухающие колебания, поддерживаемые в диссипативной системе за счет постоянного внешнего источника энергии, причем свойства этих колебаний определяются самой системой.

Автоколебания принципиально отличаются от свободных незатухающих колебаний, происходящих без действия сил, а также от вынужденных колебаний, происходящих под действием периодической силы. Автоколебательная система сама управляет внешними воздействиями, обеспечивая согласованность поступления энергии определенными порциями в нужный момент времени (в такт с ее колебаниями).

Примером автоколебательной системы могут служить часы. Храповой механизм подталкивает маятник в такт с его колебаниями. Энергия, передаваемая при этом маятнику, берется либо за счет раскручивающейся пружины, либо за счет опускающегося груза. Колебания воздуха в духовых инструментах и органных трубах также возникают вследствие автоколебаний, поддерживаемых воздушной струёй.

Автоколебательными системами являются также двигатели внутреннего сгорания, паровые турбины, ламповый генератор и т. д.

4.5 Переменный ток

4.5.1 Вынужденные электромагнитные колебания. Закон Ома для переменного тока.

Переменный ток можно рассматривать как установившиеся вынужденные электромагнитные колебания в цепи, содержащей резистор, катушку индуктивности и конденсатор. Мы будем рассматривать квазистационарные токи, для которых мгновенные значения силы тока во всех сечениях цепи практически одинаковы. Для мгновенных значений квазистационарных токов выполняются закон Ома и вытекающие из него правила Кирхгофа.

Рассмотрим процессы, происходящие в цепи, содержащей последовательно включённые резистор, катушку индуктивности, конденсатор и источник переменной Э. Д.С., изменяющейся по гармоническому закону:

где εo — амплитуда электродвижущей силы.

В цепи возникнет переменный ток, который вызовет на всех элементах цепи соответствующие падения напряжения UR, UL, UC . Будем считать, что внутреннее сопротивление источника э. д.с. пренебрежимо мало по сравнению с R. По закону Ома для участка цепи 1- L— R-2 имеем:

где φ2 — φ1 = q/C — мгновенное значение разности потенциалов обкладок

конденсатора, q — его заряд в этот же момент времени, — L(dI/dt) — э. д.с. самоиндукции в контуре. Возьмём производную по времени от обеих частей равенства (145). Учитывая, что dq/dt = I — ток в контуре, получим:

Затухающие колебания дифференциальное уравнение затухающих колебаний его решение и анализ

Учитывая, что R/L = 2δ, 1/ (ωC) = ωo2 и введя обозначение — εoω/L = еo уравнение (84) запишем в виде:

Решение уравнения (85) аналогично решению ранее рассмотренного уравнения (71). Ищем решение уравнения (84) для установившегося режима в виде:

где Iо — амплитуда переменного тока в контуре, j — сдвиг фаз между э. д.с. источника тока и силой тока. По аналогии с определением формул (74) и (75) найдём выражения для Iо и j :

(86)

(87)

Соотношение (86) называется законом Ома для переменного тока. Величина

(88)

называется полным сопротивлением цепи.

RL = ωL — индуктивное сопротивление;

RC = 1/ (ωC) — ёмкостное сопротивление;

— реактивное сопротивление. Реактивное сопротивление не вызывает тепловых потерь в цепи переменного тока. Оно создаёт сдвиг фаз между током и вынуждающей э. д.с.

R — активное сопротивление; за счёт него возникают тепловые потери в контуре.

Падение напряжения на отдельных участках цепи, представленной на рис. 15, можно получить, используя выражение (85):

UC = q/ С = U0C cos(ωt — φ — π/2);

По второму правилу Кирхгофа:

На рисунке 16 представлена векторная диаграмма амплитуд колебаний на всех элементах рассматриваемой цепи (см. рис. 15).

Из выражения (86) следует, что амплитуда тока зависит от частоты вынуждающей э. д.с. (рисунок 18). Максимального значения I0 достигает при частоте ωрез, равной:

(89)

Явление достижения током максимального значения I0рез при ω = ωрез называется резонансом напряжений. Это вызвано тем, что при ω = ωрез падения напряжений на индуктивном и ёмкостном сопротивлениях достигают максимальных значений равных по модулю и противоположных по фазе, поэтому суммарное падение напряжение на реактивном сопротивлении равно нулю. Падение напряжения на активном сопротивлении максимально, его амплитудное значение

Векторная диаграмма для резонанса напряжений приведена на рис.17.

Подставив в формулу (91) значения резонансной частоты и амплитуды напряжений на катушке индуктивности и конденсаторе, получим:

( UL )рез= ( UС )рез= I0 = U0 = Q U0, (92)

где Q — добротность контура.

Так как добротность обычных колебательных контуров больше единицы, то напряжение как на катушке индуктивности, так и на конденсаторе превышает напряжение, приложенное к цепи. Поэтому явление резонанса напряжений используется в технике для усиления колебания напряжения какой-либо определенной частоты. Например, в случае резонанса на конденсаторе, можно получить напряжение с амплитудой QUm ( в данном случае Q — добротность контура, которая может быть значительно больше Um. Это усиление напряжения возможно только для узкого интервала частот вблизи резонансной частоты контура, что позволяет выделить из многих сигналов одно колебание определенной частоты, т. е. на радиоприемнике настроиться на нужную длину волны. Явление резонанса напряжений необходимо учитывать при расчете изоляции электрических линий, содержащих конденсаторы и катушки индуктивности, так как иначе может наблюдаться их пробой.

4.5.2 Мощность, выделяемая в цепи переменного тока

Полное мгновенное значение мощности переменного тока равно произведению мгновенных значений э. д.с. и силы тока. P(t) = ε(t) I(t), где

Практический интерес представляет не мгновенное значение мощности, а ее среднее значение за период колебания. Учитывая, что =1/2, sinw t.cosw t = 0, получим

= I0 ε0 cosj (93)

Из векторной диаграммы (см. рис. 16) следует, что ε0 cosj = RI0. Поэтому

Такую же мощность развивает постоянный ток . Величины Iэф = I0 /, Uэф = U0 / называются соответственно действующими (или эффективными) значениями тока и напряжения. Все амперметры и вольтметры градуируются по действующим значениям тока и напряжения. Учитывая действующие значения тока и напряжения, выражение средней мощности можно записать в виде:

(94)

где множитель cosj называется коэффициентом мощности,

Формула (94) показывает, что мощность, выделяемая в цепи переменного тока, в общем случае зависит не только от силы тока и напряжения, но и от сдвига фаз между ними. Если в цепи реактивное сопротивление отсутствует, то cosj =1 и P = Iэф εэф. Если цепь содержит только реактивное сопротивление (R=0), то cosj = 0 и средняя мощность равна нулю, какими бы большими ни были ток и напряжение. Если cosj имеет значения, существенно меньшие единицы, то для передачи заданной мощности при данном напряжении генератора нужно увеличивать силу тока I, что приведет либо к выделению джоулевой теплоты, либо потребует увеличения сечения проводов, что повышает стоимость линий электропередачи. Поэтому на практике всегда стремятся увеличить cosj, наименьшее допустимое значение которого для промышленных установок составляет примерно 0,85.