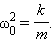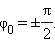- Формула Томсона
- Уравнение, описывающее процессы в колебательном контуре
- Строгий вывод формулы Томсона
- Гармонические колебания заряда и силы тока
- Формулы математического маятника
- Определение и формулы математического маятника
- Уравнение движения математического маятника
- Циклическая частота и период колебаний математического маятника
- Уравнение энергии для математического маятника
- Примеры задач с решением
- Формула томсона для пружинного маятника
- Определения пружинного маятника
- Виды пружинного маятника
- Сила упругости в пружинном маятнике
- Уравнения колебаний пружинного маятника
- Формулы периода и частоты колебаний пружинного маятника
- Формулы амплитуды и начальной фазы пружинного маятника
- Энергия колебаний пружинного маятника
- Свободные колебания пружинного маятника
- 🔥 Видео
Формула Томсона
Наша задача в первую очередь будет заключаться в определении периода (или частоты) свободных электрических колебаний. Правда, основываясь на аналогии между свободными механическими и свободными электрическими колебаниями, можно сразу записать выражения для частоты и периода свободных электрических колебаний.
Действительно, так как в формуле для циклической частоты свободных колебаний шарика на пружине 

Для периода свободных колебаний можно записать:
Формула (2.3.2) называется формулой Томсона в честь английского физика, который ее впервые вывел.
Полученные нами результаты правильны. Однако все же считать их достаточно строго доказанными нельзя. Необходимо показать, что уравнение, описывающее электрические колебания в контуре, в математическом отношении не отличается от уравнения, описывающего свободные механические колебания. Лишь после этого мы с полной уверенностью сможем утверждать, что механические и электрические колебания управляются одними и теми же количественными законами. А это и есть самое важное.
Уравнение, описывающее процессы в колебательном контуре
Основное уравнение для процессов в колебательном контуре можно записать, используя закон Ома в дифференциальной форме:
Здесь i — плотность тока, γ — удельная проводимость, 


Рассмотрим колебательный контур, содержащий все три основных элемента: конденсатор емкостью С, катушку индуктивностью L и резистор сопротивлением R (рис. 2.7).
Сопротивлением катушки, пластин конденсатора и соединительных проводов пренебрежем. Весь контур между точками 1 и 2 разобьем на малые элементы 

Теперь просуммируем уравнения (2.3.4), записанные для всех элементов 
Выясним физический смысл каждого из членов уравнения (2.3.5). Рассмотрим сумму в левой части уравнения. Для всей цепи, кроме резистора, удельная проводимость бесконечна, так как мы сопротивление этой части цепи полагаем пренебрежимо малым. Далее, будем считать резистор состоящим из тонкой проволоки постоянного поперечного сечения площадью S и постоянной удельной проводимости γ. Тогда плотность тока 

где i — сила тока в цепи.
При этих предположениях
где i длина проволоки резистора.
есть не что иное, как сопротивление резистора.
Рассмотрим первый член правой части уравнения (2.3.5). Он численно равен работе кулоновского поля, созданного поверхностными зарядами проводника, при перемещении единичного заряда вдоль контура от точки 1 к точке 2, т. е. разности потенциалов (или напряжению) на конденсаторе:
где q — заряд правой пластины конденсатора.
Второй член правой части уравнения (2,3.5) численно равен работе сторонних сил (вихревого электрического поля) в контуре по перемещению единичного заряда, т. е. представляет собой ЭДС самоиндукции. Согласно закону электромагнитной индукции:
Теперь силу тока выразим через производную заряда конденсатора. Здесь имеется небольшая тонкость. При выбранном направлении обхода контура сила тока, направленного от правой пластины конденсатора, положительна. Эта пластина разряжается и ее заряд уменьшается. Изменение заряда Δq за малый интервал времени Δt отрицательно. Для того чтобы сила тока была положительной величиной, ее надо определить так:
Если бы вместо заряда q правой пластины мы взяли заряд левой пластины, то i = +q’. В напхем случае справедливо равенство (2.3.10). Окончательно уравнение (2.3.5) запишем в форме:
Это и есть основное уравнение для процессов в колебательном контуре. Оно аналогично уравнению (1.9.5) с правой частью, равной нулю. (Такое уравнение будет описывать свободные затухающие колебания.)
Строгий вывод формулы Томсона
Решение уравнения (2.3.11) в общем случае, т. е. нахождение зависимости заряда и силы тока от времени, слипхком сложно. Мы ограничимся случаем, когда резистор в контуре отсутствует и членом iR = -q’R можно пренебречь. Тогда уравнение (2.3.11) упрощается и его можно записать в виде
Теперь, наконец, вы в полной мере сможете оценить те усилия, которые были затрачены для изучения колебаний груза на пружине и математического маятника. Ведь уравнение (2.3.12) ничем, кроме обозначений, не отличается от уравнения (1.2.4), описывающего колебания груза на пружине. При замене m ⇒ L, аx = х» ⇒ q», k ⇒ 
Но уравнение (1.2.4) или эквивалентное ему уравнение (1.4.1) нами уже решено. Поэтому, зная, как колеблется груз, мы сразу можем сказать, как происходят колебания в контуре.
Разделив правую и левую части уравнения (2.3.12) на L и введя обозначение
А это то же самое, что и уравнение (1.4.1). В уравнении (1.4.1) ω0 — циклическая частота колебаний. Значит, и величина ω0, определяемая выражением (2.3.13), тоже является частотой колебаний, но теперь уже частотой электрических колебаний (заряда, силы тока и других величин). Период свободных колебаний в контуре равен:
Это и есть формула Томсона.
Конечно, и без каких-либо уравнений мы могли бы сообразить, что период Т должен увеличиваться с ростом индуктивности L и емкости С. Действительно, при увеличении L сила тока медленнее нарастает со временем и медленнее падает до нуля. А чем больше емкость, тем большее время требуется для перезарядки конденсатора. Но получить формулу (2.3.15) строго без уравнения (2.3.14) мы бы не смогли.
Гармонические колебания заряда и силы тока
Подобно тому, как координата при механических колебаниях меняется по гармоническому закону, точно также заряд конденсатора меняется по закону синуса или косинуса:
Здесь qm — амплитуда колебаний заряда, а φ0 — начальная фаза колебаний. Эти величины определяются начальными условиями, т. е. значениями заряда и силы тока в начальный момент времени: q(0) = q0 и i(0) = i0.
Если в начальный момент времени q(0) = q0, а i(0) = i0, то колебания совершаются по косинусоидальному закону с нулевой начальной фазой* и амплитудой qm = q0:
Точно так же изменяется координата груза на пружине, если вы вывели груз из положения равновесия и не сообщили ему начальной скорости.
Сила тока также совершает гармонические колебания. Если q = q0 cos (ω0t + φ0), то
где Im = ωqm — амплитуда колебаний силы тока. Колебания силы тока смещены по фазе относительно колебаний заряда на 
Колебания заряда и силы тока для этого случая графически представлены на рисунке 2.8.
В действительности из-за энергетических потерь колебания будут затухающими. Чем больше сопротивление R, тем больше будет период колебаний. При достаточно большом сопротивлении колебания не возникают. Конденсатор разрядится, но перезарядки не произойдет.
* Именно такой случай описан в § 2.2, когда колебания в контуре начинались после замыкания цепи предварительно заряженного конденсатора.
Видео:Математические и пружинные маятники. 11 класс.Скачать

Формулы математического маятника
Видео:математический маятник ЕГЭ ФИЗИКА колебания частота периодСкачать

Определение и формулы математического маятника
Математический маятник — это колебательная система, являющаяся частным случаем физического маятника, вся масса которого сосредоточена в одной точке, центре масс маятника.
Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.
Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.
Видео:Математический маятник или откуда формула периодаСкачать

Уравнение движения математического маятника
Математический маятник — классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:
где $varphi $ — угол отклонения нити (подвеса) от положения равновесия.
Решением уравнения (1) является функция $varphi (t):$
где $alpha $ — начальная фаза колебаний; $_0$ — амплитуда колебаний; $_0$ — циклическая частота.
Колебания гармонического осциллятора — это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.
Видео:Период математического маятника. В школе обманывали?Скачать

Циклическая частота и период колебаний математического маятника
Циклическая частота математического маятника зависит только от длины его подвеса:
Период колебаний математического маятника ($T$) в этом случае равен:
Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.
Видео:Классические уравнения | математический маятник | вывод через второй закон НьютонаСкачать

Уравнение энергии для математического маятника
При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:
где $E_k$ — кинетическая энергия маятника; $E_p$ — потенциальная энергия маятника; $v$ — скорость движения маятника; $x$ — линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол — смещение связан с $x$ как:
Максимальное значение потенциальной энергии математического маятника равно:
Максимальная величина кинетической энергии:
где $h_m$ — максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m=_0x_m$ — максимальная скорость.
Видео:Почти всё о маятникеСкачать

Примеры задач с решением
Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?
Решение. Сделаем рисунок.
Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:
Из уравнения (1.1) найдем искомую высоту:
Ответ. $h=frac$
Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit
Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:
Выразим из нее ускорение:
Проведем вычисления ускорения силы тяжести:
Ответ. $g=9,87 frac$
Видео:Колебания математического и пружинного маятников. 9 класс.Скачать

Формула томсона для пружинного маятника
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.
Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению (см. §2.1):
В этом соотношении – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:
Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .
Таким образом, груз некоторой массы , прикрепленный к пружине жесткости , второй конец которой закреплен неподвижно (рис. 2.2.1), составляют систему, способную в отсутствие трения совершать свободные гармонические колебания. Груз на пружине называют линейным гармоническим осциллятором .
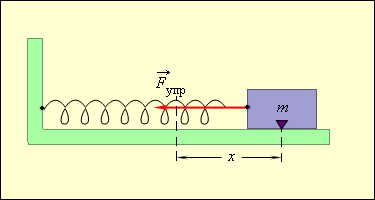 |
| Рисунок 2.2.1. |
Круговая частота свободных колебаний груза на пружине находится из второго закона Ньютона:
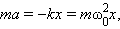 |
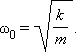 |
Частота называется собственной частотой колебательной системы.
Период гармонических колебаний груза на пружине равен
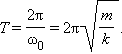 |
При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину , равную
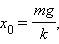 |
и колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты и периода колебаний справедливы и в этом случае.
Строгое описание поведения колебательной системы может быть дано, если принять во внимание математическую связь между ускорением тела и координатой : ускорение является второй производной координаты тела по времени :
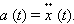 |
Поэтому второй закон Ньютона для груза на пружине может быть записан в виде
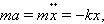 |
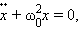 |
где
Все физические системы (не только механические), описываемые уравнением (*), способны совершать свободные гармонические колебания, так как решением этого уравнения являются гармонические функции вида
| m cos . |
Уравнение (*) называется уравнением свободных колебаний . Следует обратить внимание на то, что физические свойства колебательной системы определяют только собственную частоту колебаний или период . Такие параметры колебательного процесса, как амплитуда m и начальная фаза , определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени.
Если, например, груз был смещен из положения равновесия на расстояние и затем в момент времени отпущен без начальной скорости, то m = , .
Если же грузу, находившемуся в положении равновесия, с помощью резкого толчка была сообщена начальная скорость 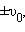
Таким образом, амплитуда m свободных колебаний и его начальная фаза определяются начальными условиями .
Существует много разновидностей механических колебательных систем, в которых используются силы упругих деформаций. На рис. 2.2.2 показан угловой аналог линейного гармонического осциллятора, совершающий крутильные колебания. Горизонтально расположенный диск висит на упругой нити, закрепленной в его центре масс. При повороте диска на угол возникает момент сил упругой деформации кручения:
Это соотношение выражает закон Гука для деформации кручения. Величина аналогична жесткости пружины . Второй закон Ньютона для вращательного движения диска записывается в виде (см. §1.23)
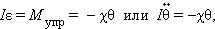 |
где – момент инерции диска относительно оси, проходящий через центр масс, – угловое ускорение.
По аналогии с грузом на пружине можно получить:
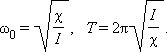 |
Крутильный маятник широко используется в механических часах. Его называют балансиром. В балансире момент упругих сил создается с помощью спиралевидной пружинки.
Сохранение энергии при колебаниях математического маятника
При гармонических колебаниях полная механическая энергия системы сохраняется (остается постоянной).
Полная механическая энергия математического маятника складывается из кинетической энергии и потенциальной энергии:
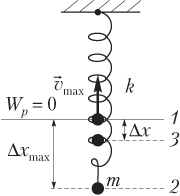
где W k — кинетическая энергия, W k = = mv 2 /2; W p — потенциальная энергия, W p = mgh ; m — масса груза; g — модуль ускорения свободного падения; v — модуль скорости груза; h — высота подъема груза над положением равновесия (рис. 10.15).
В Международной системе единиц энергия механической колебательной системы измеряется в джоулях (1 Дж).
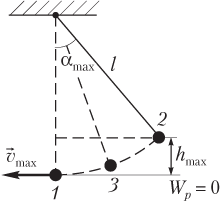
При гармонических колебаниях математический маятник проходит ряд последовательных состояний, поэтому целесообразно рассмотреть энергию математического маятника в трех положениях (см. рис. 10.15):
1) в положении равновесия ( 1 ) скорость тела имеет максимальное значение v max , поэтому кинетическая энергия также максимальна:
W k max = m v max 2 2 ;
потенциальная энергия равна нулю; полная энергия совпадает с максимальной кинетической энергией:
2) в крайнем положении ( 2 ) тело поднято над исходным уровнем на максимальную высоту h max , поэтому потенциальная энергия также максимальна:
W p max = m g h max ;
кинетическая энергия равна нулю; полная энергия совпадает с максимальной потенциальной энергией:
3) в промежуточном положении ( 3 ) тело обладает мгновенной скоростью v и поднято над исходным уровнем на некоторую высоту h , поэтому полная энергия представляет собой сумму
E = m v 2 2 + m g h ,
где mv 2 /2 — кинетическая энергия; mgh — потенциальная энергия; m — масса груза; g — модуль ускорения свободного падения; v — модуль скорости груза; h — высота подъема груза над положением равновесия.
При гармонических колебаниях математического маятника полная механическая энергия сохраняется:
Значения полной энергии математического маятника в трех его положениях отражены в табл. 10.1.
| № | Положение | W p | W k | E = W p + W k |
|---|---|---|---|---|
| 1 | Равновесие | m v max 2 / 2 | m v max 2 / 2 | |
| 2 | Крайнее | mgh max | mgh max | |
| 3 | Промежуточное (мгновенное) | mgh | mv 2 /2 | mv 2 /2 + mgh |
Значения полной механической энергии, представленные в последнем столбце табл. 10.1, имеют равные значения для любых положений маятника, что является математическим выражением закона сохранения полной механической энергии :
m v max 2 2 = m g h max ;
m v max 2 2 = m v 2 2 + m g h ;
m g h max = m v 2 2 + m g h ,
где m — масса груза; g — модуль ускорения свободного падения; v — модуль мгновенной скорости груза в положении 3 ; h — высота подъема груза над положением равновесия в положении 3 ; v max — модуль максимальной скорости груза в положении 1 ; h max — максимальная высота подъема груза над положением равновесия в положении 2 .
Угол отклонения нити математического маятника от вертикали (рис. 10.15) определяется выражением
cos α = l − h l = 1 − h l ,
где l — длина нити; h — высота подъема груза над положением равновесия.
Максимальный угол отклонения α max определяется максимальной высотой подъема груза над положением равновесия h max :
cos α max = 1 − h max l .
Пример 11. Период малых колебаний математического маятника равен 0,9 с. На какой максимальный угол от вертикали будет отклоняться нить, если, проходя положение равновесия, шарик движется со скоростью, равной 1,5 м/с? Трение в системе отсутствует.
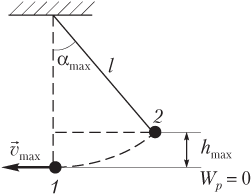
Решение . На рисунке показаны два положения математического маятника:
- положение равновесия 1 (характеризуется максимальной скоростью шарика v max );
- крайнее положение 2 (характеризуется максимальной высотой подъема шарика h max над положением равновесия).
Искомый угол определяется равенством
cos α max = l − h max l = 1 − h max l ,
где l — длина нити маятника.
Максимальную высоту подъема шарика маятника над положением равновесия найдем из закона сохранения полной механической энергии.
Полная энергия маятника в положении равновесия и в крайнем положении определяется следующими формулами:
E 1 = m v max 2 2 ,
где m — масса шарика маятника; v max — модуль скорости шарика в положении равновесия (максимальная скорость), v max = 1,5 м/с;
где g — модуль ускорения свободного падения; h max — максимальная высота подъема шарика над положением равновесия.
Закон сохранения полной механической энергии:
m v max 2 2 = m g h max .
Выразим отсюда максимальную высоту подъема шарика над положением равновесия:
h max = v max 2 2 g .
Длину нити определим из формулы для периода колебаний математического маятника
Подставим h max и l в выражение для косинуса искомого угла:
cos α max = 1 − 2 π 2 v max 2 g 2 T 2
и произведем вычисление с учетом приблизительного равенства π 2 = 10:
cos α max = 1 − 2 ⋅ 10 ⋅ ( 1,5 ) 2 10 2 ⋅ ( 0,9 ) 2 = 0,5 .
Отсюда следует, что максимальный угол отклонения составляет 60°.
Строго говоря, при угле 60° колебания шарика не являются малыми и пользоваться стандартной формулой для периода колебаний математического маятника неправомерно.
Сохранение энергии при колебаниях пружинного маятника
Полная механическая энергия пружинного маятника складывается из кинетической энергии и потенциальной энергии:
где W k — кинетическая энергия, W k = mv 2 /2; W p — потенциальная энергия, W p = k (Δ x ) 2 /2; m — масса груза; v — модуль скорости груза; k — коэффициент жесткости (упругости) пружины; Δ x — деформация (растяжение или сжатие) пружины (рис. 10.16).
В Международной системе единиц энергия механической колебательной системы измеряется в джоулях (1 Дж).
При гармонических колебаниях пружинный маятник проходит ряд последовательных состояний, поэтому целесообразно рассмотреть энергию пружинного маятника в трех положениях (см. рис. 10.16):
1) в положении равновесия ( 1 ) скорость тела имеет максимальное значение v max , поэтому кинетическая энергия также максимальна:
W k max = m v max 2 2 ;
потенциальная энергия пружины равна нулю, так как пружина не деформирована; полная энергия совпадает с максимальной кинетической энергией:
2) в крайнем положении ( 2 ) пружина имеет максимальную деформацию (Δ x max ), поэтому потенциальная энергия также имеет максимальное значение:
W p max = k ( Δ x max ) 2 2 ;
кинетическая энергия тела равна нулю; полная энергия совпадает с максимальной потенциальной энергией:
3) в промежуточном положении ( 3 ) тело обладает мгновенной скоростью v , пружина имеет в этот момент некоторую деформацию (Δ x ), поэтому полная энергия представляет собой сумму
E = m v 2 2 + k ( Δ x ) 2 2 ,
где mv 2 /2 — кинетическая энергия; k (Δ x ) 2 /2 — потенциальная энергия; m — масса груза; v — модуль скорости груза; k — коэффициент жесткости (упругости) пружины; Δ x — деформация (растяжение или сжатие) пружины.
При смещении груза пружинного маятника от положения равновесия на него действует возвращающая сила , проекция которой на направление движения маятника определяется формулой
где x — смещение груза пружинного маятника от положения равновесия, x = ∆ x , ∆ x — деформация пружины; k — коэффициент жесткости (упругости) пружины маятника.
При гармонических колебаниях пружинного маятника полная механическая энергия сохраняется:
Значения полной энергии пружинного маятника в трех его положениях отражены в табл. 10.2.
| № | Положение | W p | W k | E = W p + W k |
|---|---|---|---|---|
| 1 | Равновесие | m v max 2 / 2 | m v max 2 / 2 | |
| 2 | Крайнее | k (Δ x max ) 2 /2 | k (Δ x max ) 2 /2 | |
| 3 | Промежуточное (мгновенное) | k (Δ x ) 2 /2 | mv 2 /2 | mv 2 /2 + k (Δ x ) 2 /2 |
Значения полной механической энергии, представленные в последнем столбце таблицы, имеют равные значения для любых положений маятника, что является математическим выражением закона сохранения полной механической энергии :
m v max 2 2 = k ( Δ x max ) 2 2 ;
m v max 2 2 = m v 2 2 + k ( Δ x ) 2 2 ;
k ( Δ x max ) 2 2 = m v 2 2 + k ( Δ x ) 2 2 ,
где m — масса груза; v — модуль мгновенной скорости груза в положении 3 ; Δ x — деформация (растяжение или сжатие) пружины в положении 3 ; v max — модуль максимальной скорости груза в положении 1 ; Δ x max — максимальная деформация (растяжение или сжатие) пружины в положении 2 .
Пример 12. Пружинный маятник совершает гармонические колебания. Во сколько раз его кинетическая энергия больше потенциальной в тот момент, когда смещение тела из положения равновесия составляет четверть амплитуды?
Решение . Сравним два положения пружинного маятника:
- крайнее положение 1 (характеризуется максимальным смещением груза маятника от положения равновесия x max );
- промежуточное положение 2 (характеризуется промежуточными значениями смещения от положения равновесия x и скорости v → ).
Полная энергия маятника в крайнем и промежуточном положениях определяется следующими формулами:
E 1 = k ( Δ x max ) 2 2 ,
где k — коэффициент жесткости (упругости) пружины; ∆ x max — амплитуда колебаний (максимальное смещение от положения равновесия), ∆ x max = A ;
- в промежуточном положении —
E 2 = k ( Δ x ) 2 2 + m v 2 2 ,
где m — масса груза маятника; ∆ x — смещение груза от положения равновесия, ∆ x = A /4.
Закон сохранения полной механической энергии для пружинного маятника имеет следующий вид:
k ( Δ x max ) 2 2 = k ( Δ x ) 2 2 + m v 2 2 .
Разделим обе части записанного равенства на k (∆ x ) 2 /2:
( Δ x max Δ x ) 2 = 1 + m v 2 2 ⋅ 2 k Δ x 2 = 1 + W k W p ,
где W k — кинетическая энергия маятника в промежуточном положении, W k = mv 2 /2; W p — потенциальная энергия маятника в промежуточном положении, W p = k (∆ x ) 2 /2.
Выразим из уравнения искомое отношение энергий:
W k W p = ( Δ x max Δ x ) 2 − 1
и рассчитаем его значение:
W k W p = ( A A / 4 ) 2 − 1 = 16 − 1 = 15 .
В указанный момент времени отношение кинетической и потенциальной энергий маятника равно 15.
Работа большинства механизмов основана на простейших законах физики и математики. Довольно большое распространение получило понятие пружинного маятника. Подобный механизм получил весьма широкое распространение, так как пружина обеспечивает требуемую функциональность, может быть элементом автоматических устройств. Рассмотрим подробнее подобное устройство, принцип действия и многие другие моменты подробнее.
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Определения пружинного маятника
Как ранее было отмечено, пружинный маятник получил весьма широкое распространение. Среди особенностей можно отметить следующее:
- Устройство представлено сочетанием груза и пружины, масса которой может не учитываться. В качестве груза может выступать самый различный объект. При этом на него может оказываться воздействие со стороны внешней силы. Распространенным примером можно назвать создание предохранительного клапана, который устанавливается в системе трубопровода. Крепление груза к пружине проводится самым различным образом. При этом используется исключительно классический винтовой вариант исполнения, который получил наиболее широкое распространение. Основные свойства во многом зависят от типа применяемого материала при изготовлении, диаметра витка, правильности центровки и многих других моментов. Крайние витки часто изготавливаются таким образом, чтобы могли воспринимать большую нагрузку при эксплуатации.
- До начала деформации полная механическая энергия отсутствует. При этом на тело не влияет сила упругости. Каждая пружина имеет исходное положение, которое она сохраняет на протяжении длительного периода. Однако, за счет определенной жесткости происходит фиксация тела в начальном положении. Имеет значение то, каким образом прикладывается усилие. Примером назовем то, что она должна быть направлена вдоль оси пружины, так как в противном случае есть вероятность появления деформации и многих других проблем. У каждой пружины есть свои определенный придел сжатия и растяжения. При этом максимальное сжатие представлено отсутствием зазора между отдельными витками, при растяжении есть момент, когда происходит невозвратная деформация изделия. При слишком сильном удлинении проволоки происходит изменение основных свойств, после чего изделие не возвращается в свое первоначальное положение.
- В рассматриваемом случае колебания совершаются за счет действия силы упругости. Она характеризуется довольно большим количество особенностей, которые должны учитываться. Воздействие упругости достигается за счет определенного расположения витков и типа применяемого материала при изготовлении. При этом сила упругости может действовать в обе стороны. Чаще всего происходит сжатие, но также может проводится растяжение – все зависит от особенностей конкретного случая.
- Скорость перемещения тела может варьировать в достаточно большом диапазоне, все зависит от того, какое оказывается воздействие. К примеру, пружинный маятник может перемещать подвешенный груз в горизонтальной и вертикальной плоскости. Действие направленного усилия во многом зависит от вертикальной или горизонтальной установки.
В целом можно сказать, что пружинный маятник определение довольно обобщенное. При этом скорость перемещения объекта зависит от различных параметров, к примеру, величины приложенного усилия и других моментов. Перед непосредственным проведением расчетов проводится создание схемы:
- Указывается опора, к которой крепится пружина. Зачастую для ее отображения рисуется линия с обратной штриховкой.
- Схематически отображается пружина. Она часта представлена волнистой линией. При схематическом отображении не имеет значение длина и диаметральный показатель.
- Также изображается тело. Оно не должно соответствовать размерам, однако имеет значение место непосредственного крепления.
Схема требуется для схематического отображения всех сил, которые оказывают влияние на устройство. Только в этом случае можно учесть все, что влияет на скорость перемещения, инерцию и многие другие моменты.
Пружинные маятники применяются не только при расчетах ил решении различных задач, но также и на практике. Однако, не все свойства подобного механизма применимы.
Примером можно назвать случай, когда колебательные движения не требуются:
- Создание запорных элементов.
- Пружинные механизмы, связанные с транспортировкой различных материалов и объектов.
Проводимые расчеты пружинного маятника позволяют подобрать наиболее подходящий вес тела, а также тип пружины. Она характеризуется следующими особенностями:
- Диаметр витков. Он может быть самым различным. От показателя диаметра во многом зависит то, сколько требуется материала для производства. Диаметр витков также определяет то, какое усилие должно прикладываться для полного сжатия или частичного растяжения. Однако, увеличение размеров может создать существенные трудности с установкой изделия.
- Диаметр проволоки. Еще одним важным параметром можно назвать диаметральный размер проволоки. Он может варьировать в широком диапазоне, зависит прочность и степень упругости.
- Длина изделия. Этот показатель определяет то, какое усилие требуется для полного сжатия, а также какой упругостью может обладать изделие.
- Тип применяемого материала также определяет основные свойства. Чаще всего пружина изготавливается при применении специального сплава, который обладает соответствующие свойствами.
При математических расчетах многие моменты не учитываются. Усилие упругости и многие другие показатели выявляются путем расчета.
Видео:Урок 92 (осн). Колебательное движение. МаятникиСкачать

Виды пружинного маятника
Выделяют несколько различных видов пружинного маятника. Стоит учитывать, что классификация может проводится по типу устанавливаемой пружины. Среди особенностей отметим:
- Довольно большое распространение получили вертикальные колебания, так как в этом случае на груз не оказывается сила трения и другое воздействие. При вертикальном расположении груза существенно увеличивается степень воздействия силы тяжести. Распространен этот вариант исполнения при проведении самых различных расчетов. За счет силы тяжести есть вероятность того, что тело в исходной точке будет совершать большое количество инерционных движений. Этому также способствует упругость и инерция движения тела в конце хода.
- Также применяется горизонтальный пружинный маятник. В этом случае груз находится на опорной поверхности и на момент перемещения также возникает трение. При горизонтальном расположении сила тяжести работает несколько иначе. Горизонтальное расположение тела получило широкое распространение в различных задачах.
Рассчитывается движение пружинного маятника можно при использовании достаточно большого количества различных формул, который должны учитывать воздействие всех сил. В большинстве случаев устанавливается классическая пружина. Среди особенностей отметим следующее:
- Классическая витая пружина сжатия сегодня получила весьма широкое распространение. В этом случае между витками есть пространство, которое называется шагом. Пружина сжатия может и растягиваться, но зачастую она для этого не устанавливается. Отличительной особенностью можно назвать то, что последние витки выполнены в виде плоскости, за счет чего обеспечивается равномерное распределения усилия.
- Может устанавливаться вариант исполнения для растяжения. Он рассчитан на установку в случае, когда приложенное усилие становится причиной увеличения длины. Для крепления проводится размещение крючков.
Распространены оба варианта исполнения. При этом важно уделить внимание тому, чтобы сила прикладывалась параллельно оси. В противном случае есть вероятность смещения витков, что становится причиной возникновения серьезных проблем, к примеру, деформации.
Видео:Формула Томсона [Физзадачи #22]Скачать
![Формула Томсона [Физзадачи #22]](https://i.ytimg.com/vi/oWetPNqHeeA/0.jpg)
Сила упругости в пружинном маятнике
Следует учитывать тот момент, что до деформирования пружины она находится в положении равновесия. Приложенная сила может приводить к ее растягиванию и сжиманию. Сила упругости в пружинном маятнике рассчитывается в соответствии с тем, как воздействует закон сохранения энергии. Согласно принятым нормам возникающая упругость пропорциональна смещению тела. В этом случае кинетическая энергия рассчитывается по формуле: F=-kx. В данном случае применяется коэффициент жесткости пружины.
Выделяют довольно большое количество особенностей воздействия силы упругости в пружинном маятнике. Среди особенностей отметим:
- Максимальная сила упругости возникает на момент, когда тело находится на максимальном расстоянии от положения равновесия. При этом в подобном положении отмечается максимальное значение ускорение тела. Не следует забывать о том, что может проводится растягивание и сжатие пружины, оба варианта несколько отличается. При сжатии минимальная длина изделия ограничивается. Как правило, она имеет длину, равную диаметру витка умноженное на количество. Слишком большое усилие может стать причиной смещения витков, а также деформации проволоки. При растяжении есть момент удлинения, после которого происходит деформация. Сильное удлинение приводит к тому, что возникающей силы упругости недостаточно для возврата изделия в первоначальное состояние.
- При сближении тела к месту равновесия происходит существенное уменьшение длины пружины. За счет этого наблюдается постоянное снижение показателя ускорения. Все это происходит за счет воздействия усилия упругости, которая связано с типом применяемого материала при изготовлении пружины и ее особенностями. Длина уменьшается за счет того, что расстояние между витками снижается. Особенностью можно назвать равномерное распределение витков, лишь только в случае дефектов есть вероятность нарушения подобного правила.
- На момент достижения точки равновесия сила упругости снижается до нуля. Однако, скорость не снижается, так как тело движется по инерции. Точка равновесия характеризуется тем, что длина изделия в ней сохраняется на протяжении длительного периода при условии отсутствия внешнего деформирующего усилия. Точка равновесия определяется в случае построения схемы.
- После достижения точки равновесия возникающая упругость начинает снижать скорость перемещения тела. Она действует в противоположном направлении. При этом возникает усилие, которое направлено в обратную сторону.
- Дойдя крайней точки тело начинает двигаться в противоположную сторону. В зависимости от жесткости установленной пружины подобное действие будет повторятся неоднократно. Протяженность этого цикла зависит от самых различных моментов. Примером можно назвать массу тела, а также максимальное приложенное усилие для возникновения деформации. В некоторых случаях колебательные движения практически незаметны, но они все же возникают.
Приведенная выше информация указывает на то, что колебательные движения совершаются за счет воздействия упругости. Деформация происходит за счет приложенного усилия, которое может варьировать в достаточно большом диапазоне, все зависит от конкретного случая.
Видео:Колебания математического маятникаСкачать

Уравнения колебаний пружинного маятника
Колебания пружинного маятника совершаются по гармоническому закону. Формула, по которой проводится расчет, выглядит следующим образом: F(t)=ma(t)=-mw2x(t).
В приведенной выше формуле указывается (w) радиальная частота гармонического колебания. Она свойственна силе, которая распространяется в границах применимости закона Гука. Уравнение движения может существенно отличаться, все зависит от конкретного случая.
Если рассматривать колебательное движение, то следует уделить внимание следующим моментам:
- Колебательные движения наблюдаются только в конце перемещения тела. Изначально оно прямолинейное до полного освобождения усилия. При этом сила упругости сохраняется на протяжении всего времени, пока тело находится в максимально отдаленном положении от нуля координат.
- После растяжения тело возвращается в исходное положение. Возникающая инерция становится причиной, по которой может оказываться воздействие на пружину. Инерция во многом зависит от массы тела, развитой скорости и многих других моментов.
В результате этого возникает колебание, которое может длиться в течение длительного периода. Приведенная выше формула позволяет провести расчет с учетом всех моментов.
Видео:Свободные электромагнитные колебания. 11 класс.Скачать

Формулы периода и частоты колебаний пружинного маятника
При проектировании и вычислении основных показателей также уделяется довольно много внимания частоте и периоду колебания. Косинус – периодическая функция, в которой применяется значение, неизменяемое через определенный промежуток времени. Именно этот показатель называют период колебаний пружинного маятника. Для обозначения этого показателя применяется буква Т, также часто используется понятие, характеризующее значение, обратное периоду колебания (v). В большинстве случаев при расчетах применяется формула T=1/v.
Период колебаний вычисляется по несколько усложненной формуле. Она следующая: T=2п√m/k. Для определения частоты колебания используется формула: v=1/2п√k/m.
Рассматриваемая циклическая частота колебаний пружинного маятника зависит от следующих моментов:
- Масса груза, который прикреплен к пружине. Этот показатель считается наиболее важным, так как оказывает влияние на самые различные параметры. От массы зависит сила инерции, скорость и многие другие показатели. Кроме этого, масса груза – величина, с измерением которой не возникает проблем из-за наличия специального измерительного оборудования.
- Коэффициент упругости. Для каждой пружины этот показатель существенно отличается. Коэффициент упругости указывается для определения основных параметров пружины. Зависит этот параметр от количества витков, длины изделия, расстояние между витками, их диаметра и многого другого. Определяется он самым различным образом, зачастую при применении специального оборудования.
Не стоит забывать о том, что при сильном растяжении пружины закон Гука прекращает действовать. При этом период пружинного колебания начинает зависеть от амплитуды.
Для измерения периода применяется всемирная единица времени, в большинстве случаев секунды. В большинстве случаев амплитуда колебаний вычисляется при решении самых различных задач. Для упрощения процесса проводится построение упрощенной схемы, на которой отображаются основные силы.
Видео:Выполнялка 53.Гармонические колебания.Скачать

Формулы амплитуды и начальной фазы пружинного маятника
Определившись с особенностями проходимых процессов и зная уравнение колебаний пружинного маятника, а также начальные значения можно провести расчет амплитуды и начальной фазы пружинного маятника. Для определения начальной фазы применяется значение f, амплитуда обозначается символом A.
Для определения амплитуды может использоваться формула: А=√x 2 +v 2 /w 2 . Начальная фаза высчитывается по формуле: tgf=-v/xw.
Применяя эти формулы можно провести определение основных параметров, которые применяются при расчетах.
Видео:9. Колебания физического маятникаСкачать

Энергия колебаний пружинного маятника
Рассматривая колебание груза на пружине нужно учитывать тот момент, что при движение маятника может описываться двумя точками, то есть оно носит прямолинейный характер. Этот момент определяет выполнение условий, касающихся рассматриваемой силы. Можно сказать, что полная энергия потенциальная.
Провести расчет энергии колебаний пружинного маятника можно при учете всех особенностей. Основными моментами назовем следующее:
- Колебания могут проходить в горизонтальной и вертикальной плоскости.
- Ноль потенциальной энергии выбирается в качестве положения равновесия. Именно в этом месте устанавливается начало координат. Как правило, в этом положении пружина сохраняет свою форму при условии отсутствия деформирующей силы.
- В рассматриваемом случае рассчитываемая энергия пружинного маятника не учитывает силу трения. При вертикальном расположении груза сила трения несущественна, при горизонтальном тело находится на поверхности и при движении может возникнуть трение.
- Для расчета энергии колебания применяется следующая формула: E=-dF/dx.
Приведенная выше информация указывают на то, что закон сохранения энергии выглядит следующим образом: mx 2 /2+mw 2 x 2 /2=const. Применяемая формула говорит о следующем:
- Максимальная кинетическая энергия установленного маятника прямо пропорциональна максимальному значению потенциальной.
- На момент осциллятора среднее значение обоих сил равны.
Провести определение энергии колебания пружинного маятника можно при решении самых различных задач.
Видео:Я не смог назвать математический маятник, что делать?😅Скачать

Свободные колебания пружинного маятника
Рассматривая то, чем вызваны свободные колебания пружинного маятника следует уделить внимание действию внутренних сил. Они начинают формироваться практически сразу после того, как телу было передано движение. Особенности гармонических колебаний заключаются в нижеприведенных моментах:
- Могут также возникать и другие типы сил воздействующего характера, который удовлетворяют все нормы закона, называются квазиупругими.
- Основными причинами действия закона могут быть внутренние силы, которые формируются непосредственно на момент изменения положения тела в пространстве. При этом груз обладает определенной массой, усилие создается за счет фиксации одного конца за неподвижный объект с достаточной прочностью, второго за сам груз. При условии отсутствия трения тело может совершать колебательные движения. В этом случае закрепленный груз называется линейным.
Не стоит забывать о том, что существует просто огромное количество различных видов систем, в которых осуществляется движение колебательного характера. В них также возникает упругая деформация, которая становится причиной применения для выполнения какой-либо работы.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
🔥 Видео
Выполнялка 146.Длина математического маятникаСкачать

Урок 353. Колебательный контурСкачать

Тема 8. Колебательный контур. Свободные электромагнитные колебания в контуре. Формула ТомсонаСкачать

Теормех. 2021-окт-18. Группа ПМФ. Двойной маятникСкачать

Период колебаний колебательного контура Формула ТомсонаСкачать