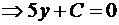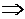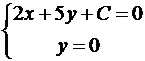Запишите уравнение прямой которая проходит через точку м 1 8 и параллельна оси абсцисс

Условие

Записать уравнения прямых, которые проходят
через точку А (3, — 1) и параллельны:

а) оси абсцисс;
б) оси ординат;
в) биссектрисе первого координатного
угла;
г) прямой у = 3х + 9.

Ответ: а) у = — i; б) х= 3;
в) у = х — 4; г) y=3x — 10.

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Запиши уравнение прямой параллельной оси ox и проходящей через точку a 1 8

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Уравнение параллельной прямой

Альтернативная формула:
Прямая, проходящая через точку M₁(x₁; y₁) и параллельная прямой Ax+By+C=0 , представляется уравнением

назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения параллельной прямой (см. также как составить уравнение перпендикулярной прямой).

Пример №2 . Написать уравнение прямой, параллельной прямой 2x + 5y = 0 и образующей вместе с осями координат треугольник, площадь которого равна 5.
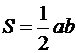
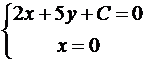
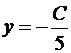
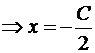
Решение. Так как прямые параллельны, то уравнение искомой прямой 2x + 5y + C = 0. Площадь прямоугольного треугольника , где a и b его катеты. Найдем точки пересечения искомой прямой с осями координат:
;
.
Итак, A(-C/2,0), B(0,-C/5). Подставим в формулу для площади: 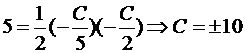. Получаем два решения: 2x + 5y + 10 = 0 и 2x + 5y – 10 = 0 .

Пример №3 . Составить уравнение прямой, проходящей через точку (-2; 5) и параллельной прямой 5x-7y-4=0 .
Решение. Данную прямую можно представить уравнением y = 5 /₇x – 4 /₇ (здесь a = 5 /₇). Уравнение искомой прямой есть y – 5 = 5 / 7(x – (-2)), т.е. 7(y-5)=5(x+2) или 5x-7y+45=0 .

Пример №4 . Решив пример 3 (A=5, B=-7) по формуле (2), найдем 5(x+2)-7(y-5)=0.

Пример №5 . Составить уравнение прямой, проходящей через точку (-2;5) и параллельной прямой 7x+10=0.
Решение. Здесь A=7, B=0. Формула (2) дает 7(x+2)=0, т.е. x+2=0. Формула (1) неприменима, так как данное уравнение нельзя разрешить относительно y (данная прямая параллельна оси ординат).

Видео:12. Уравнения прямой в пространстве Решение задачСкачать

Прямая линия. Уравнение прямой.

Свойства прямой в евклидовой геометрии.

Через любую точку можно провести бесконечно много прямых.

Через любые две несовпадающие точки можно провести единственную прямую.

Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются

параллельными (следует из предыдущего).

В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:

• прямые пересекаются;

• прямые параллельны;

• прямые скрещиваются.

Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия

задается на плоскости уравнением первой степени (линейное уравнение).

Общее уравнение прямой.

Определение. Любая прямая на плоскости может быть задана уравнением первого порядка

причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим

уравнением прямой. В зависимости от значений постоянных А, В и С возможны следующие частные случаи:

• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

• А = 0, В ≠0, С ≠0 — прямая параллельна оси Ох

• В = 0, А ≠0, С ≠ 0 – прямая параллельна оси Оу

• В = С = 0, А ≠0 – прямая совпадает с осью Оу

• А = С = 0, В ≠0 – прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных

Уравнение прямой по точке и вектору нормали.

Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В)

перпендикулярен прямой , заданной уравнением

Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1).

Решение. Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С

подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно

С = -1. Итого: искомое уравнение: 3х – у – 1 = 0.

Уравнение прямой, проходящей через две точки.

Пусть в пространстве заданы две точки M 1 ( x 1 , y 1 , z 1 ) и M2 ( x 2, y 2 , z 2 ), тогда уравнение прямой,

проходящей через эти точки:

Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На

плоскости записанное выше уравнение прямой упрощается:

Дробь = k называется угловым коэффициентом прямой.

Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Решение. Применяя записанную выше формулу, получаем:

Уравнение прямой по точке и угловому коэффициенту.

Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:

и обозначить , то полученное уравнение называется

уравнением прямой с угловым коэффициентом k.

Уравнение прямой по точке и направляющему вектору.

По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание

прямой через точку и направляющий вектор прямой.

Определение. Каждый ненулевой вектор (α₁, α₂), компоненты которого удовлетворяют условию

Аα₁ + Вα₂ = 0 называется направляющим вектором прямой.

Пример. Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).

Решение. Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением,

коэффициенты должны удовлетворять условиям:

1 * A + (-1) * B = 0, т.е. А = В.

Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.

при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение:

Уравнение прямой в отрезках.

Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим:

или , где

Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения

прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.

Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.

С = 1, , а = -1, b = 1.

Нормальное уравнение прямой.

Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется

нормирующем множителем, то получим

xcosφ + ysinφ — p = 0 – нормальное уравнение прямой.

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Уравнение параллельной прямой

Как составить уравнение прямой параллельной данной прямой и проходящей через данную точку?

Пусть y = k₁x+b₁ — данная прямая. С учётом условия параллельности прямых уравнение прямой, параллельной данной, имеет вид y = k₁x+b₂.

Так как эта прямая проходит через точку M(x_o; y_o), то её координаты удовлетворяют уравнению прямой. Подставив в уравнение x_o и y_o, мы найдем b:

1) Составить уравнение прямой, которая проходит через точку A(4;21) и параллельна прямой y=3x-8.

Так как угловые коэффициенты у параллельных прямых равны, то k₂=k₁=3 и уравнение прямой, параллельной прямой y=3x-8, имеет вид y=3x+b. Так как искомая прямая проходит через точку A(4;21), подставляем в уравнение прямой координаты A (x=4; y=21):

21=3·4+b, откуда находим b: b= 21-12= 9.

Итак, уравнение прямой, параллельной прямой y=3x-8, проходящей через точку A(4;21) — y=3x+9.

2) Написать уравнение прямой, параллельной прямой x=5, проходящей через точку B(-3; 5).

Так как прямая x=5 параллельна оси Oy, то и параллельная ей прямая также параллельна Oy, а значит, уравнение этой прямой имеет вид x=a.

Так как эта прямая проходит через точку B(-3; 5), то её абсцисса удовлетворяет уравнению прямой: a= -3.

Итак, уравнение прямой, параллельной прямой x=5 и проходящей через точку B(-3; 5) — x= -3.

3) Написать уравнение прямой, параллельной прямой y= -11, проходящей через точку K(2; 4).

Так как прямая y= -11 параллельна оси Ox, то и параллельная ей прямая также параллельна оси Ox. Поэтому уравнение прямой имеет вид y=b.

Поскольку эта прямая проходит через точку K(2; 4), то её ордината удовлетворяет уравнению прямой: b=4.

Уравнение прямой, параллельной прямой y= -11 и проходящей через точку K(2; 4) — y=4.

Видео:Составляем уравнение прямой по точкамСкачать

Практика. Решение задач. Часть 1. Уравнения прямой

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Мы изучили новые инструменты – координаты и действия с векторами в координатах, операцию скалярного умножения векторов. Этот урок мы посвятим решению задач и потренируемся применять эти новые инструменты на практике.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Напишите уравнение прямой, проходящей через точку N( — 2 ; 3) и параллельной оси абсцисс?

Геометрия | 5 — 9 классы

Напишите уравнение прямой, проходящей через точку N( — 2 ; 3) и параллельной оси абсцисс.

Функция параллельна оси абсцисс, то нам нужен только y точки.

В данном случае он равен 3, следовательно функция = &gt ; y = 3.

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Запишите уравнения прямых, параллельных осям координат и проходящим через точку А( — 2 ; 7)?

Запишите уравнения прямых, параллельных осям координат и проходящим через точку А( — 2 ; 7).

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Составьте уравнение прямой проходящей через точку А(1 ; — 2), если она : а)параллельна оси абсцисс ; б)перпендикулярна оси абсцисс (пожалуйста напишите полно)?

Составьте уравнение прямой проходящей через точку А(1 ; — 2), если она : а)параллельна оси абсцисс ; б)перпендикулярна оси абсцисс (пожалуйста напишите полно).

Видео:Уравнение параллельной прямойСкачать

Составьие уравнение прямой, проходящей через точку А(1 ; — 2), если она : а) параллельна оси абцисс ; б) перпендикулярна оси абцисс?

Составьие уравнение прямой, проходящей через точку А(1 ; — 2), если она : а) параллельна оси абцисс ; б) перпендикулярна оси абцисс.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Составьте уравнение прямой, проходящей через точку А(1 ; — 2), если она : 1) параллельна оси абсцисс ; 2)перпендикулярна оси абсцисс?

Составьте уравнение прямой, проходящей через точку А(1 ; — 2), если она : 1) параллельна оси абсцисс ; 2)перпендикулярна оси абсцисс.

Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Составьте уравнение прямой проходящей через точку А(1 ; — 2) если она 1)параллельна оси абсцисс, 2)перпендикулярна оси абсцисс?

Составьте уравнение прямой проходящей через точку А(1 ; — 2) если она 1)параллельна оси абсцисс, 2)перпендикулярна оси абсцисс.

Видео:№972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать

Составьте уравнение прямой, проходящей через точку А(1 ; — 2), если она : а) параллельна оси абсцисс ; б) перпендикулярна оси абсцисс?

Составьте уравнение прямой, проходящей через точку А(1 ; — 2), если она : а) параллельна оси абсцисс ; б) перпендикулярна оси абсцисс.

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Составьте уравнение прямой проходящей через точки A(2 ; — 3) и B(4 ; 1) ?

Составьте уравнение прямой проходящей через точки A(2 ; — 3) и B(4 ; 1) .

Найдите координаты точки пересечения данной прямой с осью абсцисс.

Видео:Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

Составьте уравнение прямой, проходящей через точку А(1 : — 2), если она : а)параллельна оси абсцисс : б)перпендикулярна оси абсцис?

Составьте уравнение прямой, проходящей через точку А(1 : — 2), если она : а)параллельна оси абсцисс : б)перпендикулярна оси абсцис.

Видео:УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Составьте уравнение прямой, проходящей через точку В ( — 3 ; 8) и образует с положительным направлением оси абсцисс угол 135 °?

Составьте уравнение прямой, проходящей через точку В ( — 3 ; 8) и образует с положительным направлением оси абсцисс угол 135 °.

Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать

Окружность задана уравнением [tex] x ^ + (y — 1) ^ = 4[ / tex] напишите уравнение прямой, проходящей через ее центр и параллельной оси абсцисс?

Окружность задана уравнением [tex] x ^ + (y — 1) ^ = 4[ / tex] напишите уравнение прямой, проходящей через ее центр и параллельной оси абсцисс.

ПРОШУ РЕШЕНИЕ И ПОЛНОЕ ПОЯСНЕНИЕ.

На этой странице сайта вы найдете ответы на вопрос Напишите уравнение прямой, проходящей через точку N( — 2 ; 3) и параллельной оси абсцисс?, относящийся к категории Геометрия. Сложность вопроса соответствует базовым знаниям учеников 5 — 9 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

Дай ответ на мой вопрос пожалуйста.

Знаю только в 3. Ответ : 35. Т. к диагональ AC делит угол BCD пополам. Т. е угол BCA = 70 / 2 = 35. Следовательно уголBAC = 35(т. К треугольник ABC равнобедренный.

2)∆ABD — равнобедренный, значит угли при основании равны, то есть уголADB = углуBAD = 70° Угол АВD = 180° — (70° + 70°) = 40° угол CBA = 180° — ABD = 180° — 40° = 140° 3)Угол СВА = углу МВN как вертикальный ∆MBN — равнобедренный, значит углы при осно..

150 / 2 = 75(360 — 150) / 2 = 105 ответ 75, 75, 105, 105(Но это не точно).

Кажется вот такое решение.

Параллельные прямые отсекают на секущих пропорциональные отрезки.

V = (4ПR ^ 3) / 3 = (4×3, 14×3 ^ 3) / 3 = 113, 04 куб. Метр.

Давай рассмотрим прямоугольник АМК, АК = 2(потому что у нас АК = КС , а равны АК = КС так как МКперпендикулярноАС) давай решим задачу по теореме Пифагора с ^ 2 = а ^ 2 + в ^ 2 с ^ 2 = 2 ^ 2 + 5 ^ 2 с ^ 2 = 29 с = √29 АМ = √29.

Если треугольники равны значит при наложении одного треугольника на другой их вершины совпадут, поэтому A = Е = 40° B = F = 60° C = G = 80° ___________________ во втором то же свойство равных треугольников ABC = PQR = XYZ AB = PQ = XY = 5 см BC = QR ..

Подписывать по часовой стрелке, е = 40, В = 60, с = 80. Они же равны.

🎦 Видео

Уравнение окружности (1)Скачать

Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать

Видеоурок "Уравнение прямой, проходящей через две точки"Скачать

Уравнение прямой на плоскости. Решение задачСкачать