Запишите уравнение по 2 му закону кирхгофа для контура авсд

Видео:Применение законов Кирхгофа при решении задачСкачать

Постоянный ток

Господа, всем привет!

Сегодня мы рассмотрим второй закон Кирхгофа. Он чуть сложнее, чем первый закон Кирхгофа, который мы уже рассматривали ранее, поэтому я сперва дам общую формулировку, а потом мы постараемся аккуратно разобраться во всем этом деле.

Итак, второй закон Кирхгофа гласит, что алгебраическая сумма ЭДС, действующих в контуре равна алгебраической сумме падений напряжения в ветвях контура. Может быть сложновато для восприятия, если вы читаете это в первый раз, не спорю. Но сейчас попробуем разобраться более детально во всем этом. Для начала давайте определим, что же такое контур электрической цепи, где эти самые ЭДС действуют. Пожалуй, это тот случай, когда проще нарисовать картинку, чем объяснять словами. Взглянем на рисунок 1.

Рисунок 1 – Контура в схеме

На нем мы можем видеть три контура: я обозначил их красным, оранжевым и синим цветами. То есть контур – это некоторая замкнутая часть электрической цепи, состоящая из нескольких ветвей.

То есть что говорит второй закон Кирхгофа? У нас есть большая и сложная электрическая схема. В ней много различных контуров. Будем рассматривать подробно один из этих контуров, любой на выбор. И вот если мы в этом контуре сложим ЭДС всех источников, какие там есть, то их сумма будет равна сумме падений напряжения на всех сопротивлениях этого контура. И это верно для любого контура в нашей схеме. Довольно интересный факт. И если про первый закон Кирхгофа можно говорить, что он интуитивно очевиден, то здесь, вообще говоря, это не совсем так. А поскольку он не очевиден на первый взгляд, тем больше поводов показать его верность математически.

Господа, прошу обратить внимание на рисунок 2. На нем изображен один из контуров какой-то сложной электрической схемы.

Рисунок 2 – Контур схемы

Почему он именно такой, можете вы спросить? Да просто так! Я рисовал его так, как подскажет фантазия в тот момент. Вы можете смело заявить, что ваша фантазия лучше и нарисовать какой-либо другой контур с другими компонентами. Потом повторите все действия, которые я буду производить над этим контуром, и в конечном счете у вас должен получиться точно такой же результат, как и у меня.

Первым делом давайте зададимся направлением обхода контура. Это некоторое направление в контуре, которое мы принимаем за положительное. Можно в какой-то степени назвать это аналогом осей координат в математике. Направление обхода контура у нас по часовой стрелке, и я показал его синей стрелочкой на рисунке 2.

Следующим шагом нам надо расставить предполагаемое направление токов в каждой ветви. Тут опять же все целиком отдается вашей фантазии. На данном этапе можно рисовать любое направление токов. Если мы угадали – отлично, если нет – в конце всех расчетов получим ток с другим знаком. Я расставил на рисунке 2 все токи черными стрелками и рядом с ними подписал их величины (I₁…I₄).

А теперь внимание, господа. Пришло время вспомнить то выражение, ради получения которого я написал предыдущую статью. На всякий случай, если вдруг кто забыл, напоминаю его

Оно означает, что если потенциалы на концах ветви равны φ₁ и φ₂, то их разность равна ЭДС источника в ветви минус произведение тока в ветви на сопротивление в ветви.

Применим это выражение для каждой ветви нашего контура, изображенного на рисунке 2. Поскольку у нас в контуре четыре ветви, то всего мы получим четыре уравнения. Резонный вопрос – а как быть со знаками при записи этих уравнений? Правила тут два.

• Если направление работы источника напряжения совпадает с направлением обхода контура, то берем его со знаком плюс. Если не совпадает – со знаком минус. Совсем просто: если стрелка в источнике напряжения совпадает со стрелкой обхода, то Е в уравнении пишется без изменения знака, если стрелки в разные стороны – то надо поставить минус перед E.
• Если направление тока, которое мы сами выбрали чуть раньше, совпадает с направлением обхода, то в нашем уравнении перед произведением тока на сопротивление так и остается знак минус. Если они направлены в разные стороны, то знак минус меняем на плюс.

Пользуясь этими простыми правилами, запишем уравнения для каждой ветви.

Очевидно, что если в цепи нет источника ЭДС, то у нас не будет первого слагаемого в правой части. А если нет сопротивления, то не будет второго слагаемого в правой части. Собственно, это и видно из составленных уравнений.

Господа, надеюсь вы помните, что с уравнениями в одной системе можно творить всякие интересные штуки? Например, можно все их сложить между собой (правые и левые части). Легко заметить, что при сложении всех этих четырех уравнений в левой части будет нолик, то есть все потенциалы волшебным образом самоликвидируются. Сделаем это! Получим

А теперь давайте перенесем все слагаемые с ЭДС в одну сторону, а с током и сопротивлением – в другую. Имеем

А имеем мы, собственно, второй закон Кирхгофа. Все честно, как я и писал в начале – алгебраическая сумма ЭДС, действующих в контуре равна алгебраической сумме падений напряжения в ветвях контура. Надеюсь, господа, после статьи про закон Ома у вас не возникает вопросов, почему произведение тока на сопротивление – это падение напряжения на сопротивлении? Если возникает – срочно, очень срочно, прямо сейчас пройдитесь по этой ссылке и разрешите эти вопросы!

А что же все-таки тут понимается под словом алгебраическая сумма? Это словосочетание нам уже встречалось. Это значит, что складывать надо с учетом знака. А как выбирать правильно этот самый знак? Господа, взгляните еще разок на рисунок 2. Там у нас задано направление обхода контура и направление токов. Все это мы выбирали (я бы даже сказал придумывали) сами. Ну и направление работы источника еще видно по его графическому изображению.

Так вот, если направление работы источника ЭДС совпадает с направлением обхода контура, то мы ему приписываем знак плюс, а если не совпадает – минус. Аналогично и для правой части. Если направление тока совпадет с направлением обхода, то мы пишем произведение тока на сопротивление со знаком плюс. Иначе – со знаком минус.

Специально для труЪ-математиков привожу запись второго закона Кирхгофа с использованием хитрых значков суммирования. Вне всякого сомнения, если вы будете использовать эту запись, то произведете впечатление человека, который шарит в теме!

Здесь у нас N источников c ЭДС E_i и M ветвей с сопротивлениями R_j и токами I_j. Разумеется, суммирование идет все так же с учетом знаков.

Может возникнуть резонный вопрос: «Как же так? Получается, я сам все придумываю: и направление обхода, и направление токов и это значит, что знак может получиться любой. Поверну стрелку тока в другую сторону и сразу знак у слагаемого поменяется! Но ведь в реальной схеме токи всегда текут в своем направлении вне зависимости от того, что я там нарисую на листочке! Какое-то противоречие!» Господа, вопрос весьма справедливый. Но предлагаю разобраться в нем в следующей статье. Сохраним некоторую интригу на текущий момент, как принято во всяких этих сериальчиках . А сейчас – спасибо, что прочитали статью, огромной вам всем удачи, и пока!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Видео:Законы Кирхгофа - самое простое и понятное объяснение этих законовСкачать

Первый и второй закон Кирхгофа

При расчете режима работы электрической цепи очень часто необходимо определить токи, напряжения и мощности на всех ее участках при заданных ЭДС источников и сопротивлений участков цепи. Данный расчёт основан на применении законов Кирхгофа.

В этой статье предполагается, что вы знакомы с определениями узла, ветви и контура.

Содержание:

Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Первый закон Кирхгофа

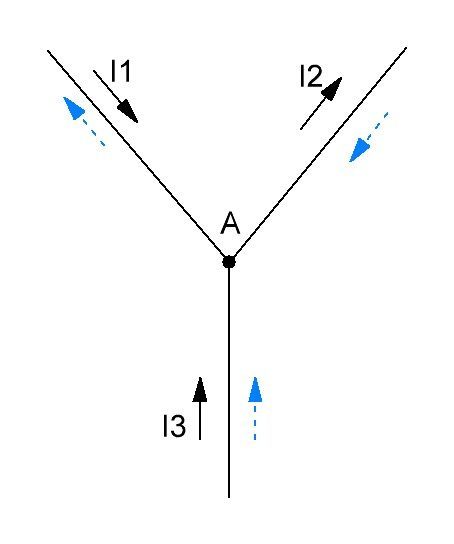
Первый закон Кирхгофа гласит, что в ветвях образующих узел электрической цепи алгебраическая сумма токов равна нулю (токи входящие в узел считаются положительными, выходящие из узла отрицательными).

Пользуясь этим законом для узла A (рисунок 1) можно записать следующее выражение:

Рисунок 1 — Первый закон Кирхгофа

I1 + I2 − I3 + I4 − I5 − I6 = 0.

Попытайтесь самостоятельно применить первый закон Кирхгофа для определения тока в ветви. На приведенной выше схеме изображены шесть ветвей образующие электрический узел В, токи ветвях входят и выходят из узла. Один из токов i неизвестен.

#1. Запишите выражение для узла В

#2. Найдите ток i

Видео:Лекция 117. Правила КирхгофаСкачать

Результат

Выбор направления токов

Если при расчёте цепи направление токов неизвестны, то при составлении уравнений согласно законом Кирхгофа их необходимо предварительно выбрать произвольно и обозначить на схеме стрелками. В действительности направление токов в ветвях могут отличаться от произвольно выбранных. Поэтому выбранные направления токов называют положительными направлениями. Если в результате расчёта цепи какие-либо токи будут выражены отрицательными числами, то действительные направления этих токов обратны выбранным положительным направлениям.

Рисунок 2

На рисунке 2,а представлен электрический узел. Произвольно, стрелками укажем направления токов (рисунок 2,б).

Важно! При выборе направления токов в ветвях, необходимо выполнения двух условий:
1. Ток должен вытекать из узла через одну или несколько других ветвей;
2. Хотя бы один ток должен входить в узел.

Предположим, что после расчёта цепи получились следующие значения токов:

I1 = -5 А;
I2 = -2 A;
I3 = 3 А.

Так как значение тока I1 и I2 получились отрицательными, следовательно, действительно направление I1 и I2 противоположно ранее выбранным (рисунок 3).

Рисунок 3 — действительное направление токов обозначено синими стрелками

• I1 − I2 + I3 = 0;
• -5 − (-2) +3 = 0;
• -I1 + I2 + I3 = 0;
• -5 + 2 +3 = 0.

Видео:Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать

Второй закон Кирхгофа.

Второй закон Кирхгофа: в контуре электрической цепи алгебраическая сумма эдс равна алгебраической сумме падений напряжения на всех сопротивлениях данного контура.

где k – число источников ЭДС; m – число ветвей в замкнутом контуре; I_i, R_i – ток и сопротивление i-й ветви.

Применение второго закона Кирхгофа

Для контура ABСDE, изображенного на рисунке 4, стрелками указаны положительные направления токов (произвольно). Составим уравнение согласно второму закону Кирхгофа. Для этого произвольно зададимся направлением обхода контура по часовой или против часовой стрелки. В данном примере направление обхода контура выберем по часовой стрелке.

Рисунок 4

При составлении уравнений по второму закону Кирхгофа, ЭДС записывается со знаком “+”, если ее направление совпадает с направлением произвольно выбранного обхода контура. В противном случае ЭДС записывается со знаком “-”.

Падения напряжения записываются со знаком “+”, если направление тока в нем совпадает с направлением обхода.

Начнём с эдс E1, так как её направление совпадает с обходом контура — записываем её со знаком “+” перед знаком равно.

Контур ABСDE E1 =

E2 направленна против обхода контура записываем со знаком “-” перед знаком равно.

Контур ABСDE E1 − E2 =

Так как больше ЭДС в контуре ABСDЕ нет — левая часть уравнения готова.

В правой части уравнения указываются падения напряжения контура, так как направления токов I1 и I2 совпадает с обходом контура – записываем падения напряжения со знаком “+”.

Контур ABСDЕE E1 − E2 = I1*R1 + I2*R2

Направление тока I3 не совпадет с обходом контура:

Контур ABСDE E1 − E2 = I1*R1 + I2*R2 − I3*R3.

Уравнение для контура готово.

Законы Кирхгофа являются основой для расчета электрической цепи, вот несколько методов применяющие данные законы.

Видео:Второй закон Кирхгофа. Смотри и изучай!Скачать

Первый и второй законы Кирхгофа

Некоторые электрические цепи можно изобразить в виде простого контура, содержащего источник питания и небольшое количество деталей — резисторов, конденсаторов или других. Но существуют и большие схемы, включающие в себя несколько замкнутых ветвей. В этих случаях важно точно рассчитать электрические параметры на любом рассматриваемом участке. Законы Кирхгофа позволяют их определить путём составления и решения нескольких простых уравнений.

Видео:Как составить уравнения по законам Кирхгофа?Скачать

Первый закон Кирхгофа

Закон Ома описывает взаимосвязь между напряжением, сопротивлением и силой тока в простых одноконтурных цепях. На практике чаще встречаются сложные разветвленные цепи, состоящие из нескольких контуров и многих узлов, которые невозможно описать, применяя стандартные правила для расчета последовательных и параллельных цепей.

Определить напряжение и силу тока в разветвленных цепях позволяют правила Кирхгофа, которые в технической литературе обычно называют законами Кирхгофа. Хотя более корректным следует считать название «правила», поскольку они не являются фундаментальными законами природы. Например, первое правило Кирхгофа вытекает из закона сохранения заряда. Оно гласит, что сумма всех токов в каждом узле электроцепи равна нулю.

Формулировка закона требует уточнения следующих терминов:

• Узел — это определённое место на схеме, в котором сходится 3 или большее количество проводов. Узлами можно назвать точки, расположенные на протяжении 1 провода, если в этих местах подсоединены ещё провода.
• Движение тока, направленного к определённому узлу, условно называют положительным, противоположное — отрицательным.

Закон Кирхгофа, если говорить простыми словами, может быть сформулирован так: сколько токов втекает в узел, столько же и вытекает. Это свидетельствует о непрерывности тока для электрической цепи. Поэтому существует ещё одна формула, выражающая первое правило Кирхгофа:

Здесь с одной стороны знака равенства рассматриваются токи, входящие в определённый узел, а с другой — выходящие.

При использовании первого закона Кирхгофа для цепи переменного тока применяются мгновенные значения напряжений, которые принято обозначать буквой İ. Расчеты в этом случае проводятся по уравнению, представленному в комплексной форме.

Видео:решение задачи составлением уравнений по правилам киргофа. Законы киргофа кратко на практикеСкачать

Второй закон Кирхгофа

Когда рассматривается электрическая цепь, подключённая к источнику тока, в каждой её точке имеется определённый потенциал. Разность между ними создаёт электрическое поле, которое вызывает перемещение зарядов.

Цепь представляет собой замкнутый контур, по которому движутся электроны. Электрическое поле выполняет определённую работу по их перемещению. Каждый заряд перемещается по цепи, а затем под действием ЭДС источника замыкает круг.

Второй закон Кирхгофа гласит, что работа по перемещению заряда вдоль любого контура электроцепи с возвратом в начальную точку равна нулю. В этой формулировке подразумевается любой замкнутый контур, причем как тот, который включает источник питания, так и о тот, где его нет.

Работа электрического поля при перемещении заряда в рассматриваемом случае представляет собой сумму падений напряжения для каждого из участков контура. Таким образом, второе правило или закон Кирхгофа гласит, что сумма напряжений всех ветвей в контуре равняется нулю. Это можно выразить в виде следующего уравнения:

Если напряжение и направление обхода контура совпадают, то U записывают со знаком плюс, в противном случае — со знаком минус. Направление обхода выбранного контура может быть определено произвольным образом. Второе правило Густава Кирхгофа его не регламентирует.

Если в контуре есть один или несколько источников питания, то формулу можно выразить следующим образом:

Здесь имеется p источников питания, q участков контура. Сумма всех ЭДС имеющихся источников питания равна сумме падений напряжения.

Видео:Метод контурных токов - определение токов. ЭлектротехникаСкачать

Значение правил Кирхгофа

Законы Кирхгофа выражают фундаментальные принципы физики. Их формулировки кажутся очень простыми и очевидными. Но на самом деле они представляют собой метод, позволяющий рассчитать электрические параметры сетей очень сложной конфигурации.

С помощью законов Кирхгофа можно составить систему независимых уравнений для расчета параметров электрической цепи. Важно, чтобы их количество было не меньше, чем число параметров, которые необходимо определить.

На приведённом рисунке представлена электроцепь, для которой будет проводиться расчёт. Используя первый закон или правило Кирхгофа, для узла A можно записать:

В этот узел входят два тока, а выходит один. Далее необходимо применить второе правило. Для этого можно выбрать внешний контур. Видно, что здесь имеется два источника тока и два резистора. Поэтому будут получены уравнения:

Здесь приведены 2 эквивалентные формулы. В левой части равенства учтены электродвижущие силы двух источников тока, в правой — падение напряжения на обоих резисторах с учётом направления токов. Ещё одно уравнение можно получить из 2 закона при обходе по правому внутреннему контуру:

В результате получена система, включающая в себя три уравнения с тремя неизвестными:

Используя конкретные данные, можно подставить в систему уравнений численные значения и найти, чему равна сила тока для каждой ветви, относящейся к узлу A. При расчётах важно понимать, что при достаточно сложной конфигурации электроцепи иногда бывает непросто определить направление силы тока для каждой ветви.

Первый и второй законы Густава Кирхгофа позволяют точно определить не только величину тока, но и его знак. Если в приведённом примере после вычисления искомых значений с помощью представленной системы уравнений окажется, что ток с индексом 2 принимает отрицательное значение, то это означает, что на самом деле он имеет направление, противоположное указанному на рисунке.

Видео:Урок 265. Задачи на правила КирхгофаСкачать

Законы для магнитного поля

Правила Кирхгофа нашли свое применение и при расчете магнитных цепей. Первый закон Кирхгофа для магнитной цепи выглядит так:

Проще говоря, сумма всех магнитных потоков, проходящих через узел, равняется нулю.

Второй закон в применении к магнитным полям звучит следующим образом: «Сумма магнитодвижущих сил в контуре равняется сумме магнитных напряжений». Формула выглядит так:

Кирхгофом выведены правила, имеющие абсолютный прикладной характер. С их помощью можно решать практические вопросы в электротехнике. Широкое применение этих правил объясняется простотой формулировки уравнений и возможностью их решения с применением стандартных способов линейной алгебры.

Видео:Метод узловых и контурных уравненийСкачать

Видео по теме

🔍 Видео

Законы Кирхгофа. Метод контурных уравненийСкачать

Правила Кирхгофа - определение токов. ЭлектротехникаСкачать

Урок 14. Законы Кирхгофа простыми словами с примерамиСкачать

Урок 263. Правила КирхгофаСкачать

Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

50. Правила КирхгофаСкачать

Второй закон КирхгофаСкачать

Второй закон Кирхгофа для электрической цепи: определение и формула. Закон Кирхгофа простыми словамиСкачать

☠#8 Урок. Законы Кирхгофа - САМОЕ ПРОСТОЕ ОБЪЯСНЕНИЕ!Скачать