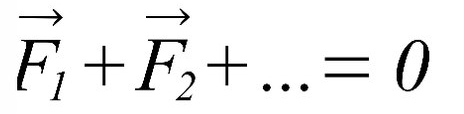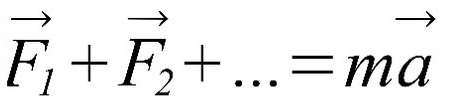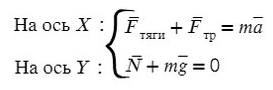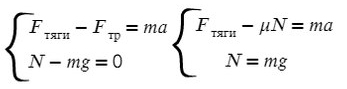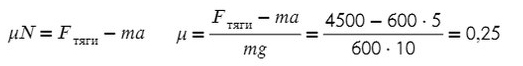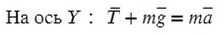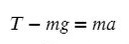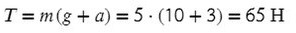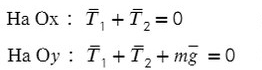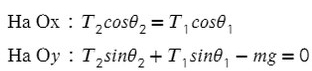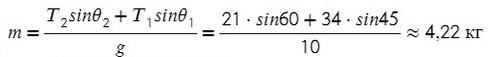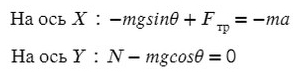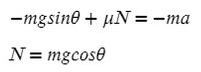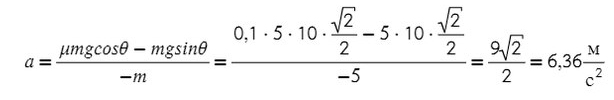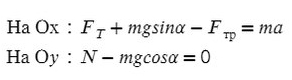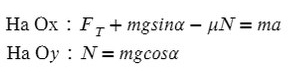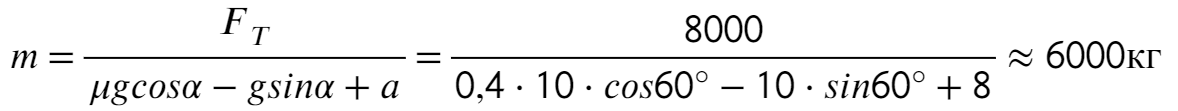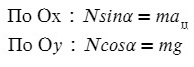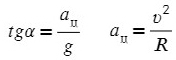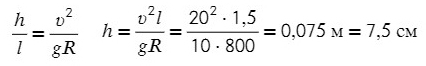Задачи по динамике.
I и II закон Ньютона.
Ввод и направление осей.
Проецирование сил на оси.
Решение систем уравнений.
Самые типовые задачи по динамике
Начнем с I и II законов Ньютона.
Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых. Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.
I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.
Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.
II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.
Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.
При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.
Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².
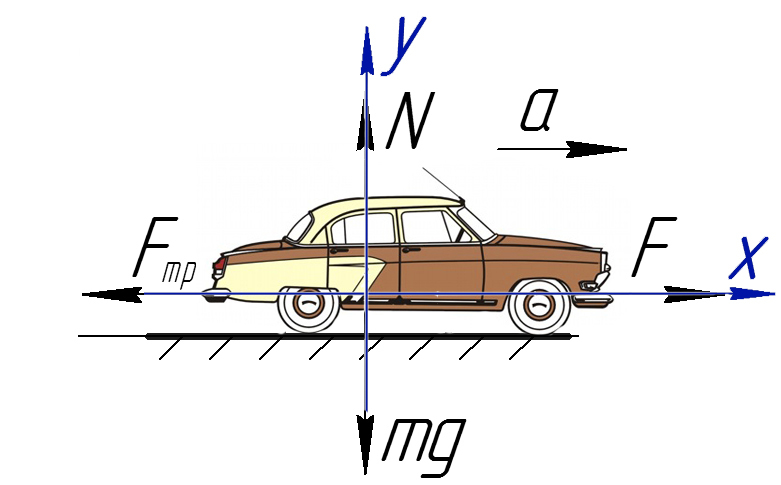
Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:
На Ось Х: движение с ускорением
На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)
Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.
По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.
Fтр = μN, где N — сила реакции опоры. На оси Y: N = mg, тогда в данной задаче Fтр = μmg.
Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.
Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.
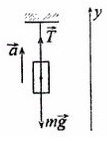
Сделаем рисунок, покажем силы, которые дествуют на груз
T — сила натяжения нити
На ось X: нет сил
Разберемся с направлением сил на ось Y:
Выразим T (силу натяжения) и подставим числительные значения:
Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.
Далеко не всегда все силы, действующие на тело, направлены вдоль осей.
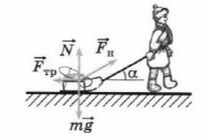
Простой пример: мальчик тянет санки
Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей.
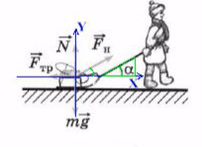
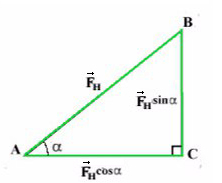
Отношение противолежащего катета к гипотенузе — это синус.
Отношение прилежащего катета к гипотенузе — это косинус.
Сила тяги на ось Y — отрезок (вектор) BC.
Сила тяги на ось X — отрезок (вектор) AC.
Если это непонятно, посмотрите задачу №4.
Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле , ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.
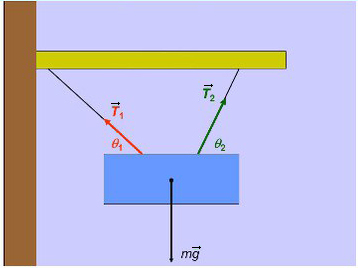
Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.
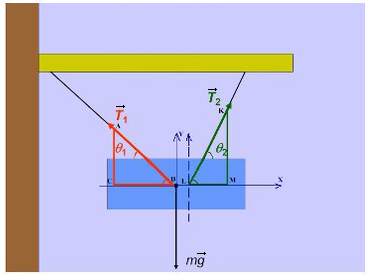
Введем оси и спроецируем силы:
Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.
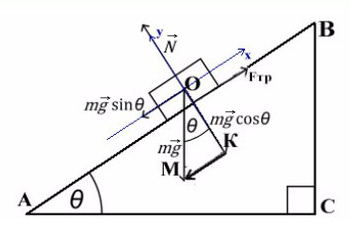
Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска?
Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).
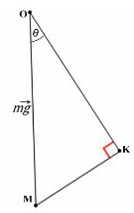
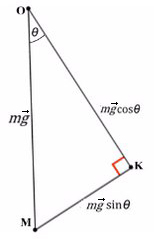
Рассмотрим поподробнее ΔKOM:
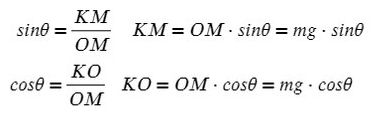
Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!
Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:
Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время.
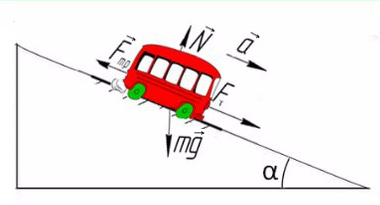
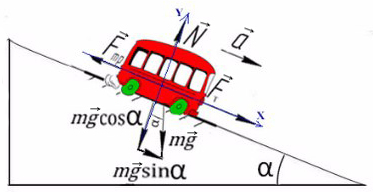
Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с² и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.
Сделаем рисунок с силами:
Введем оси X и Y. Спроецируем mg на оси:
Запишем второй закон Ньютона на X и Y:
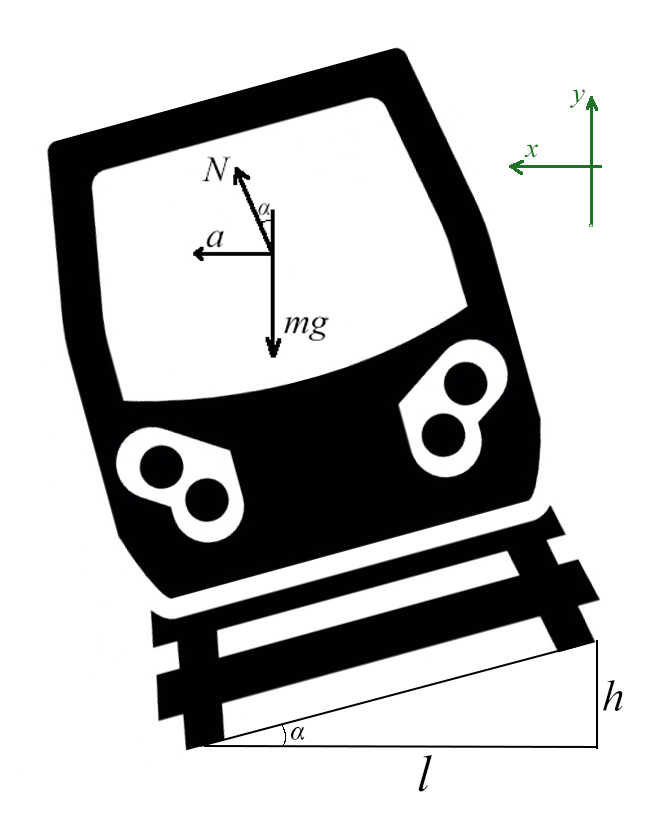
Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.
Самое сложное — понять, какие силы куда действуют, и как угол влияет на них.
Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!
Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)
Запишем какие силы действуют на оси:
Ускорение в данной задачи центростремительное!
Поделим одно уравнение на другое:
Тангенс — это отношение противолежащего катета к прилежащему:
Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.
В качестве закрепления материала решите несколько похожих задач с подсказками и ответами.
Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Запишем уравнения II закона Ньютона в векторной форме для каждого тела
Ответ: 14,8 м/с
Задача 2. Тело массой 4 кг перемещается вверх по наклонной плоскости под действием связанного с ним невесомой и нерастяжимой нитью грузом массой 12 кг. Начальные скорости тела и груза равны нулю, коэффициент трения тела о плоскость равен 0,05, угол наклона плоскости равен 30 о . Определите ускорение, с которым движется тело, и силу натяжения нити. Считать, что блок невесом и трение в блоке отсутствует.
ДАНО:  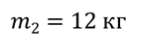    | РЕШЕНИЕ:  Запишем второй закон Ньютона для тела и груза Запишем второй закон Ньютона для тела и груза   В проекциях на ось Ох: В проекциях на ось Ох:  В проекциях на ось Оy: В проекциях на ось Оy:  В проекциях на ось О’y’: В проекциях на ось О’y’: 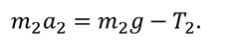 Получаем систему уравнений Получаем систему уравнений 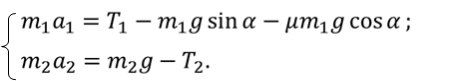 Так как нить невесома и нерастяжима, а в блоке отсутствует трение, то: Так как нить невесома и нерастяжима, а в блоке отсутствует трение, то:  С учётом последних выражений преобразуем систему уравнений С учётом последних выражений преобразуем систему уравнений 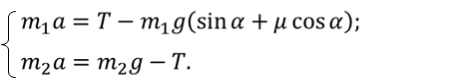 Для того, чтобы решить эту систему уравнений сложим первое и второе уравнение. Тогда получим Для того, чтобы решить эту систему уравнений сложим первое и второе уравнение. Тогда получим  Преобразуем данное уравнение и выразим искомое ускорение Преобразуем данное уравнение и выразим искомое ускорение    Теперь определим силу натяжения нити Теперь определим силу натяжения нити   |
  |
Ответ: 6,4 м/с 2 ; 43,2 Н.
Задача 3. Два груза массами т1 = 5 кг и т2 = 2 кг связаны невесомой нерастяжимой нитью, переброшенной через невесомый блок, который прикреплен к вершине призмы, и могут скользить по граням этой призмы. Определите ускорение грузов, если начальные скорости грузов равны нулю, α = 60 о , β = 30 о , а коэффициент трения — 0,3.
ДАНО: 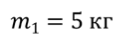   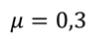  | РЕШЕНИЕ:  Запишем второй закон Ньютона для обоих грузов Запишем второй закон Ньютона для обоих грузов    В проекциях на ось Оx и O’x’: В проекциях на ось Оx и O’x’: 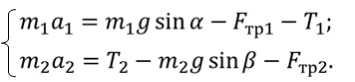 В проекциях на ось Оy и О’у’: В проекциях на ось Оy и О’у’:   С учётом последних выражений преобразуем систему уравнений в проекциях на ось Оx и O’x’: С учётом последних выражений преобразуем систему уравнений в проекциях на ось Оx и O’x’: 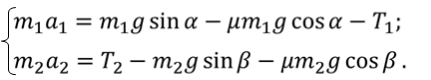 Так как нить и блок невесомы: Так как нить и блок невесомы:  Так как нить нерастяжима и в блоке нет сил трения: Так как нить нерастяжима и в блоке нет сил трения:  С учётом последних равенств сложим первое и второе уравнение системы в проекциях на ось Оx и O’x’: С учётом последних равенств сложим первое и второе уравнение системы в проекциях на ось Оx и O’x’:  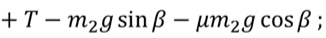  Тогда искомое ускорение равно Тогда искомое ускорение равно     |
 | О |
Ответ:а= 2,6 м/с 2 .
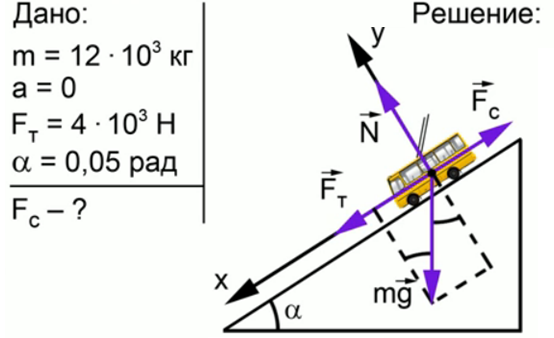
Задача 4. Троллейбус массой 12 т движется равномерно под гору с уклоном 0,05 рад при силе тяги 4 кН. Определить силу сопротивления движению.
Записываем краткое условие задачи и выполняем поясняющий чертеж :
По ох: mg* sin a + Fт – Fc = 0 при а ≤ 0,1 рад а =sin a = tq a
Ответ: 
Тема №3 « Решение задач на движение связанных тел».
Цель: Диагностика знаний учащихся, необходимых для решения задач.
Физический диктант.
Тело движется горизонтально под действием силы F = 2H, масса тела 2кг, ч = 0.2.
Уравнение движения тела x = 3+2t-0,5t 2
Зарисуйте все векторы.
Запишите II закон Ньютона в векторной форме.
Выберите оси координат и запишите закон в проекции на оси.
Найдите вес тела.
Найдите силу давления на поверхность.
Запишите уравнение зависимости Vx(t).
Найдите силу трения Fтр. (2 способа)
Ответы
1)
2) 




3) Fтр-? F = ma N — mg =0 7) 1. Fm=чN N=mg Fm=чmg; Fm=0,2*2кг*10м/с 2 = 4Н;
4) P = N = mg P=20H 2. Fm= ma+ F; Fm= 1*2Н+ 2Н = 4Н
5) Fg = N = 20Н
Закрепление и расширение знаний, умений и навыков в решении задач.
Задача №1.
Два груза, массы которых m1 = 0.1кг; m2 = 0.2кг связаны нитью и лежат на гладкой горизонтальной поверхности. К левому грузу приложена F2 = 0,5H; к правому F1 = 3H. Чему равна сила натяжения нити?
1. Изобразим все векторы сил действующие на тела.
2. Запишем уравнение II закона в векторной форме для каждого тела.
I тело 



II тело 



3. Запишем уравнение в проекциях на координатной оси.
4. Составляем систему:
a = 


5. сделайте вычисления , а так же выясните, изменится ли натяжение нити ,если силы поменять местами.
Задача №2
1. Изобразим все векторы сил действующие на тела.
Обратите внимание: нити две, соответственно силы натяжения разные Т1 и Т2.
2. Запишем уравнение II закона в векторной форме для каждого тела.
I тело: 

II тело: 




III тело: m3 

3. Запишем уравнение в проекциях на координатной оси.
4. Составляем систему:
Дорешайте в числах и найдите силу давления возникающую в оси левого блока (Fg=N) (Силу реакции действующую на ось левого блока)
Задача №3
На гладком столе лежит брусок массой 2кг, на котором лежит тело 1кг. Какую силу нужно приложить к нижнему бруску, чтобы он двигался с а = g/2? Коэффициент трения между брусками 0,5.
1. Изобразим все векторы сил действующие на тела.
Запишем уравнения II закона Ньютона в векторной форме для каждого тела










3. Запишем уравнение в проекциях на координатной оси.
Так как Fтр1 = Fтр2 , то уравнение для 2 го тела в проекции ось Y писать не обязательно!
4.Составляем систему:
F — 2чmg = mа + Ма
F = а(m + М) + 2чmg =1/2 g(m + М) + mg
F = 1/2 g(m + М + 2m) =1/2 g(М + 3m) =1/2 ·10 · 2 = 25 Н..
Задача № 4:
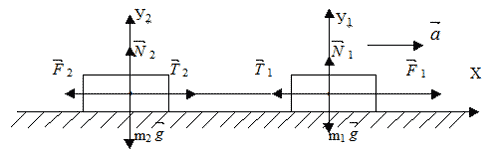
Два тела, связанные невесомой нерастяжимой нитью (см. рис.) тянут с силой 15 Н вправо по столу. Массы брусков m1= 1 кг и m2 = 4 кг, μ = 0,1.
С каким ускорением движутся бруски? Чему равна сила натяжения нити?
Ч
Сила натяжения нити на всех участках одинакова и все тела движутся с одним и тем же ускорением, т.е.
Т1 = Т2 = Т, 
Чтобы решить задачу, надо её проанализировать.
Рассмотрим все силы, действующие на каждое тело отдельно. Оба тела взаимодействуют с землёй, столом и нитью. На первое тело действуют: m1g, Т1, Fтр1, N1. На второе тело действуют: m2g, N2, T2,Fтр2 и сила F. Системы отсчета свяжем со столом.

1.Изобразим все силы, действующие на тела. Ускорение тела направлено вправо.
Из условия задачи => Т1 = Т2 = Т; 
2.Запишем II-ой закон Ньютона в общем виде ∑ 


3.Выберем координатные оси: ось ОУ направим по направлению 
а ось ОХ по направлению 
4.Проецируем векторные уравнения II закона Ньютона для I-го и II-го тела на координатные оси:
O 


Поскольку из уравнения 2 =>что Аналогично:
N2 = m2 ∙ g; то Fтр2 =μ · N2=μ ∙ m · g
N1 = m1g; то Fтр1= μ · N1 = μ ∙ m1g, тогда уравнение (1 / )II- го тела примет вид
тогда ур-ние (1)примет видF – T – μ ∙ m2 ∙ g = m2 
Т – μ · m1g = m1 
Получили два уравнения для 2-х тел, где учтены все силы, действующие на тела в отдельности.
Решаем совместно систему уравнений (3)и (3 1 ) методом почленного сложения уравнений, получаем: T – μ m1g + F – T – μ m2g = m1
F – μg (m1+ m2) = 
Откуда 
Силу натяжения нити находим из уравнения (3) или (3 1 )
Т= μ ∙ m1 · g + m1 

или Т = F – m2 

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Решение задач на равнопеременное движение в проекциях на координатные оси
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Тема сегодняшнего урока: «Решение задач динамики в проекциях на координатные оси». Мы знаем, что основная задача динамики – выяснить причины механического движения. Но существует и обратная задача: зная приложенные к телу силы, рассчитывают его движение. Как раз в этой задаче и применяется метод координат.
📺 Видео
Уравнение движенияСкачать

Урок 9. Проекции вектора на координатные осиСкачать

Определение координаты движущегося тела | Физика 9 класс #3 | ИнфоурокСкачать

Физика - уравнения равноускоренного движенияСкачать

Решение графических задач на равномерное движениеСкачать

9 класс, 3 урок, Графики прямолинейного равномерного движенияСкачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Графики зависимости кинематических величин от времени при равномерном и равноускоренном движенииСкачать

Равномерное прямолинейное движение - физика 9Скачать

Урок 3 Определение координаты движущегося телаСкачать

Проекция перемещения на ось XСкачать

Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Траектория и уравнения движения точки. Задача 1Скачать

Урок 12. Равномерное прямолинейное движениеСкачать

Как записать проекцию вектора на оси координат - bezbotvyСкачать

Основные понятия и уравнения кинематики равноускоренного движения тела.Скачать

Физика. Решение задач. Уравнение движения тела,движущегося равномерно. Выполнялка 26Скачать

Физика 10 класс (Урок№2 - Равномерное прямолинейное движение материальной точки.)Скачать