Лабораторная работа № 204
ОПРЕДЕЛЕНИЕ ВЯЗКОСТИ ЖИДКОСТИ МЕТОДОМ СТОКСА
Цель работы: изучить метод Стокса, определить коэффициент динамической вязкости глицерина.
Приборы и принадлежности:
стеклянный цилиндрический сосуд с глицерином,
1. ВЯЗКОСТЬ ЖИДКОСТИ. ЗАКОН СТОКСА
В жидкостях и газах при перемещении одних слоев относительно других возникают силы внутреннего трения, или вязкости, которые определяются законом Ньютона:
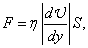
где h — коэффициент внутреннего трения, или коэффициент динамической вязкости, или просто вязкость; 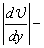
Согласно уравнению (1) коэффициент вязкости h в СИ измеряется в Па × с или в кг/( м × с ).
Механизм внутреннего трения в жидкостях и газах неодинаков, т.к. в них различен характер теплового движения молекул. Подробное изложение вязкости жидкости рассмотрено в работе № 203, вязкости газов – в работе № 205.
Вязкость жидкости обусловлена молекулярным взаимодействием, ограничивающим движение молекул. Каждая молекула жидкости находится в потенциальной яме, создаваемой соседними молекулами. Поэтому молекулы жидкости совершают колебательные движения около положения равновесия, то есть внутри потенциальной ямы. Глубина потенциальной ямы незначительно превышает среднюю кинетическую энергию, поэтому, получив дополнительную энергию при столкновении с другими молекулами, она может перескочить в новое положение равновесия. Энергия, которую должна получить молекула, чтобы из одного положения перейти в другое, называется энергией активации W , а время нахождения молекулы в положении равновесия – временем «оседлой жизни» t . Перескок молекул между соседними положениями равновесия является случайным процессом. Вероятность того, что такой перескок произойдет за время одного периода t 0 , в соответствии с законом Больцмана, составляет
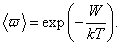
Величина, обратная вероятности перехода молекулы 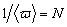
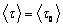
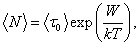
где k – постоянная Больцмана; 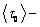
Коэффициент динамической вязкости зависит от 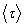
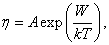
где А – константа, определяемая свойствами жидкости.
Формула (4) является приближенной, но она достаточно хорошо описывает вязкость жидкости, например, воды в интервале температур от 5 до 100 ° С, глицерина – от 0 до 200 ° С.
Из формулы (4) видно, что с уменьшением температуры вязкость жидкости возрастает. В ряде случаев она становится настолько большой, что жидкость затвердевает без образования кристаллической решетки. В этом заключается механизм образования аморфных тел.
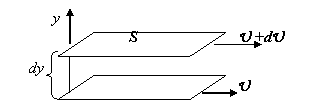
При малых скоростях движения тела в жидкости слой жидкости, непосредственно прилегающий к телу, прилипает к нему и движется со скоростью тела. По мере удаления от поверхности тела скорость слоев жидкости будет уменьшаться, но они будут двигаться параллельно. Такое слоистое движение жидкости называется ламинарным. При больших скоростях движения жидкости ламинарное движение жидкости становится неустойчивым и сменяется турбулентным, при котором частицы жидкости движутся по сложным траекториям со скоростями, изменяющимися беспорядочным образом. В результате происходит перемешивание жидкости и образуются вихри.
Характер движения жидкости определяется безразмерной величиной Re , называемой числом Рейнольдса. Это число зависит от формы тела и свойств жидкости. При движении шарика радиусом R со скоростью U в жидкости плотностью r ж
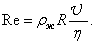
При малых Re ( — 2 мм движется со скоростью 5 — 10 см/ c в вязкой жидкости, например в глицерине, движение жидкости будет ламинарным. В этом случае на тело будет действовать сила сопротивления, пропорциональная скорости
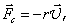
где r – коэффициент сопротивления. Для тела сферической формы
Сила сопротивления шарика радиусом R примет вид:
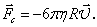
Формула (7) называется законом Стокса.
2. ОПИСАНИЕ РАБОЧЕЙ УСТАНОВКИ И МЕТОДА
Одним из существующих методов определения коэффициента динамической вязкости является метод Стокса. Суть метода заключается в следующем. Если в сосуд с жидкостью бросить шарик плотностью большей, чем плотность жидкости ( r > r ж ), то он будет падать (рис. 2). На движущийся в жидкости шарик действует сила внутреннего трения (сила сопротивления) 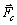
Видео:Физика. 10 класс. Течение вязкой жидкости. Формула Стокса. Обтекание тел. Лабораторная работа № 5Скачать

Рассмотрим падение шарика в вязкой жидкости
При движении шарика слой жидкости, граничащий с его поверхностью, прилипает к шарику и движется со скоростью шарика. При вычислении сопротивления среды следует учитывать трение отдельных слоев жидкости друг о друга, а не трение шарика о жидкость.
На шарик, падающий в вязкой жидкости, действуют три силы (рис. 2.2):
· 
· сила Архимеда FА = pж×V×g (равная весу жидкости в объеме шарика);
· сила сопротивления, обусловленная вязкостью жидкости:
F = 6p×h×r×v,
где rш – плотность материала шарика;
rж – плотность жидкости;
V – объем шарика;
g – ускорение свободного падения.
Все три силы направлены по вертикали: F1 – вниз, F2 и F3 – вверх.
В общем случае уравнение движения шарика имеет вид
Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение dv/dt уменьшается до тех пор, пока шарик не достигнет такой скорости, при которой ускорение равно 0.
Тогда уравнение (2.3) примет вид:
в этом случае шарик движется с постоянной скоростью v0.
Решая (2.4) относительно h, получим
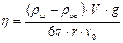
Если теперь учесть, что V = 
где d – диаметр шарика;
l – длина участка равномерного движения, пройденного за время t,
то формула (2.5) примет окончательный вид

Таким образом, для нахождения h нужно измерить d, l и t.
Рассмотрим подъем шарика в вязкой жидкости.
Если два одинаковых шарика связаны невесомой нитью, перекинутой через блок, причем один из шариков будет погружен в сосуд с жидкостью (2.3.), то уравнения движения шарика имеют вид:

В уравнениях (2.7)
I – момент инерции диска;
R – радиус диска;
Т1 и Т2 – натяжение нитей,
Fтр – сила трения, обусловленная вязкостью жидкости,
FА – сила Архимеда.
Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение уменьшается до тех пор, пока шарик не достигнет такой скорости v0, при которой ускорение равно 0.
Тогда уравнения (2.7), при 

В этом случае шарик двигается с постоянной скоростью. Из (2.8) следует

или аналогично формуле (2.6) расчетная формула принимает вид:

В формуле (2.10) так же как и в формуле (2.6) нужно измерить d, l, t.
Описание установки.
Длинный стеклянный цилиндр, наполненный исследуемой жидкостью, имеет две горизонтальные метки А и В, расположенные на расстоянии l друг от друга. Метка А установлена так, что при прохождении через нее шарик уже имеет постоянную скорость v0 (см. рис 2.2).
При измерении вязкости при подъеме шарика применяется схема (рис. 2.3): на краю стеклянного цилиндра установлен блок, через который перекинуты шарики, связанные нитью. Для определения вязкости при подъеме шарика, один шарик опускают на дно цилиндра с жидкостью.
Видео:Вязкость и течение Пуазёйля (видео 14) | Жидкости | ФизикаСкачать

Лабораторная работа по физике Метод стокса вариант 87. Лабораторная работа 2.1.вариант 87. Отчет по лабораторной работе 1 Определение коэффициента динамической вязкости жидкости методом Стокса
| Название | Отчет по лабораторной работе 1 Определение коэффициента динамической вязкости жидкости методом Стокса |
| Анкор | Лабораторная работа по физике Метод стокса вариант 87 |
| Дата | 26.11.2021 |
| Размер | 81.8 Kb. |
| Формат файла |  |
| Имя файла | Лабораторная работа 2.1.вариант 87 .docx |
| Тип | Отчет #282577 |
 С этим файлом связано 1 файл(ов). Среди них: 02_Русский язык.docx. С этим файлом связано 1 файл(ов). Среди них: 02_Русский язык.docx.  Показать все связанные файлы Подборка по базе: Отчет по лабораторной работе № 3.docx, Отчет по лабораторной работе № 1 (образец).docx, Отчёт №2 по лабораторной работе на тему Механические колебания.d, 7. Отчет УПН.docx, Отчет по лабораторной работе №2.docx, ОБРАЗЕЦ ОТЧЕТА.pdf, Требования к содержанию отчёта по лабораторной работе (1).docx, Бух (фин) отчетность-Практические задания (7).docx, Отчет по лабораторной работе маятник Обербека (1).pdf, Образец отчета по практики (преддипломн ой).docx.docx Показать все связанные файлы Подборка по базе: Отчет по лабораторной работе № 3.docx, Отчет по лабораторной работе № 1 (образец).docx, Отчёт №2 по лабораторной работе на тему Механические колебания.d, 7. Отчет УПН.docx, Отчет по лабораторной работе №2.docx, ОБРАЗЕЦ ОТЧЕТА.pdf, Требования к содержанию отчёта по лабораторной работе (1).docx, Бух (фин) отчетность-Практические задания (7).docx, Отчет по лабораторной работе маятник Обербека (1).pdf, Образец отчета по практики (преддипломн ой).docx.docxМинистерство образования и науки Российской Федерации ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Отчет по лабораторной работе № 2.1 Студент группы КНбз-20-1_____________Д.А. Коровкин Различают два типа течения вязкой жидкости – ламинарное и турбулентное. Турбулентным называется такое течение жидкости, при котором её частицы совершают неустановившееся и неупорядоченные движения по сложным траекториям, приводящим к перемешиванию слоёв. Ламинарное – это упорядоченное течение жидкости, при котором траектории движения соседних частиц мало отличаются друг от друга. При ламинарном течении жидкость можно рассматривать как совокупность отдельных слоёв, движущихся с различными скоростями. Это обусловлено тем, что при движении слоев жидкости относительно друг друга с различными скоростями между ними возникает тормозящая сила, это сила внутреннего трения или сила вязкости. Вязкость – это свойство жидкости оказывать противодействие перемещению её слоёв относительно друг друга. Природа этих сил заключается в том, что слои жидкости, движущиеся с разными скоростями, обмениваются энергией: слои с молекулами, имеющими большую скорость, передают некоторое количество движения более медленным слоям, ускоряя их, но при этом сами подвергаются торможению. Ньютон показал, что сила внутреннего трения, действующая на средние слои, прямо пропорциональна градиенту скорости слоев в направлении, перпендикулярном течению: Градиент скорости – это изменение скорости двух слоёв жидкости dV на расстоянии между слоями dX. Коэффициент динамической вязкости зависит от природы жидкости и уменьшается с повышением ее температуры. Закон Ньютона определяет также силу трения, возникающую на границе между жидкостью и движущимся в ней твердым телом, например, шариком. Метод Стокса. Стоксом был предложен метод определения , основанный на анализе движения шарика, свободно падающего в вязкой жидкости. Это возможно если плотность материала шарика ш больше плотности жидкости ж в которой он движется. Характер его движения определяется тремя действующими на него силами (рис. 2): силой тяжести где т – масса шарика; Особенность силы вязкого трения заключается в том, что ее величина зависит от скорости движения тела относительно жидкости. При малых скоростях эта зависимость прямо пропорциональная. В начале, при увеличении скорости тела сила трения возрастает настолько, что движение становится равномерным. Если тело имеет постоянную скорость, т.е. движение установившееся, то Выразим составляющие силы, входящие в уравнение (3) через параметры жидкости и шарика. Для тел сферической формы, модуль силы вязкого трения определяется формулой Стокса: где r – радиус шарика; V – скорость его движения относительно жидкости. Важно отметить, что формула (4) справедлива только в случае ламинарного течения жидкости относительно шарика (скорость движения шарика должна быть небольшой), а жидкость по всем направлениям простирается безгранично, т.е. размеры сосуда, в котором находится жидкость, должны быть много больше по сравнению с размерами шарика. Условия ламинарности можно считать выполненными, если число Рейнольдса Re кр где ?ж — плотность жидкости, а критическое значение числа Рейнольдса для шарика Re кр , движущегося в жидкости можно принять равным единицы. Выразим массу шарика через его плотность и объем а выражение для архимедовой силы принимает вид: Подставляя выражения (4), (6) и (7) в уравнение (3), и учитывая, что d=2r, после простых преобразований получим Ц На цилиндре имеются метки 3 и 4. Расстояние между метками L можно замерить при помощи линейки 6, а диаметр шарика – при помощи микрометра. Время прохождения между метками 3 и 4 можно определить с помощью секундомера 5. Метка 3 помещена на несколько сантиметров ниже верхнего уровня жидкости для выполнения условия равномерного движения шарика в жидкости; V = const на участке L. Цилиндр закрыт пробкой с воронкой, в которую опускается шарик, двигающийся в дальнейшем примерно по оси цилиндра так, чтобы на его движение не влияли стенки. При более точных измерениях необходимо учитывать влияние размеров стеклянного цилиндра. Эксперимент можно проводить как на физической, так и на виртуальной модели установки. 𝜌ш = (7,8 ± 0,1) ∙ 10 3 кг/м 3 . 1. Получить свой вариант задания и допуск к работе у ведущего преподавателя. Свой вариант (значения L и d) можно взять из таблицы в приложении по номеру зачётной книжки, в нашем случае это: 2. Ознакомился с работой виртуальной лабораторной установки. 3. Провел пробные измерения для различных значений диаметра шарика d и расстояния между метками L, определяя время прохождения между метками при помощи секундомера. 4. Занес в таблицу заданные в вашем варианте значения: расстояние Liмежду метками 3 и 4 (см. рис.3), диаметр шарика di и его плотность ρш, а также плотность исследуемой жидкости ρж. 5. Сбросив шарик в сосуд с жидкостью. В момент касания шариком верхней метки запустил секундомер, а в момент касания шариком нижней метки остановил его. Записал в таблицу показание секундомера ti. 6. Кнопкой “СБРОС” установил нуль на табло секундомера. 7. Повторил измерения пять раз, задавая различные значения диаметра шариков di и расстояние Li между метками (пункт 3 и 4). 8. Результаты опытов занесены в таблицу измерений. Таблица 1
Пример расчета для первого эксперимента таблицы 1: скорость шарика 𝑣1 = L1 /t1 9. Вычислить коэффициент вязкости η для каждого из пяти опытов по рабочей формуле (7). Число Рейнольдса 10. Найти среднее значение коэффициента вязкости 11.Определить абсолютные приборные погрешности прямых измерений (расстояния между метками ∆L, диаметра шарика ∆d, времени его падения ∆t, плотности шарика ∆ρш и жидкости ∆ρж), а также их относительные ошибки εL , εd , ερ и εt. ∆L=0.5 см дано в таблице вариантов; ∆d=0.05 см дано в таблице вариантов; ∆t=0,1 с, так как секундомер цифровой, цена деления его составляет 0,1 с. 12.Оценить полную абсолютную ∆η и относительную ε погрешности. здесь количество экспериментов n = 5, доверительная вероятность α = 0,95, коэффициент Стьюдента t0,95;5 = 2,8.
14. Сравнить полученное значение η со справочными данными. Полученный экспериментальным путем диапазон значений η = 1,47 ± 0,05 (Па с) включает в себя табличное значение коэффициента вязкости для глицерина при комнатной температуре (20 0 С)
15. По результатам эксперимента сделали вывод: в ходе выполнения работы изучили явления внутреннего трения в жидкостях и опытным путем определили величины коэффициента вязкости жидкости методом Стокса на виртуальной лабораторной установке. 🔥 ВидеоОпределение коэффициента вязкости жидкости методом СтоксаСкачать  Определение коэффициента вязкости водного раствора глицерина методом СтоксаСкачать  9 класс, 6 урок, Уравнение окружностиСкачать  Вращательное движение. 10 класс.Скачать  Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать  Уравнение Мещерского и формула Циолковского LIVE | 11 класс, студенты МФТИ | Вузовская физика с FСкачать  Сферическое движениеСкачать  Векторное уравнение движения. Условие столкновения частиц: Иродов 1.5Скачать  Кинематика точки Задание К1Скачать  Урок 87. Движение по наклонной плоскости (ч.1)Скачать  вывод центростремительного ускоренияСкачать  🔴Я сдам ОГЭ! по физике. Занятие #10. Механические явленияСкачать  Вязкость жидкости 500 сПСкачать  Урок 15. Решение задач на графики движенияСкачать  Вращательное движение твёрдого тела. Задачи 1, 2, 3Скачать  Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать  Естественный способ задания движенияСкачать  Конический маятник представляет собой маленький шарик, закрепленный на нити - №22706Скачать  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
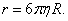

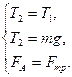

 , выталкивающей силой Архимеда
, выталкивающей силой Архимеда  и силой вязкого трения
и силой вязкого трения  . Уравнение движения шарика из основного закона динамики в данном случае принимает вид:
. Уравнение движения шарика из основного закона динамики в данном случае принимает вид: , (1)
, (1) – скорость его движения относительно жидкости;
– скорость его движения относительно жидкости;  – ускорение свободного падения. В проекции на ось 0 х, т.е. на направление движения шарика уравнение (1) запишется:
– ускорение свободного падения. В проекции на ось 0 х, т.е. на направление движения шарика уравнение (1) запишется: . (2)
. (2) и получим уравнение
и получим уравнение . (3)
. (3) (4)
(4) , (5)
, (5) , (6)
, (6) (7)
(7) . (8)
. (8)


 (Па*с)
(Па*с) (Па*с)
(Па*с) (Па*с)
(Па*с) (Па*с)
(Па*с) (Па*с)
(Па*с)





 по формуле
по формуле









