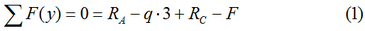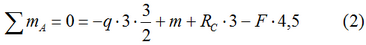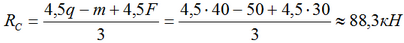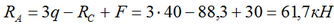Запишите систему уравнений равновесия для определения реакций в опорах двухопорной балки (6 видео)

iSopromat.ru

Пример решения задачи по расчету опорных реакций балки, закрепленной на двух шарнирных опорах и нагруженной сосредоточенной силой F, моментом m и равномерно распределенной нагрузкой q.

Содержание

Задача
Пример решения
Как определить реакции в опорах?
Что такое реакция опоры?
Что вы должны уже уметь?
Должны уметь находить сумму проекций сил
Должны уметь составлять сумму моментов относительно точки
Должны разбираться в основных видах опор
Примеры определения сил реакций опор
Определение реакций опор для балки
Определение реакций опор для балки с распределенной нагрузкой
Определение опорных реакций для плоской рамы
Определение реакций опор балки – решение задачи
Как определить реакции опор балки
Пример решения задачи на определение реакций опор балки
Решение задачи
Уравнения равновесия для сил
Уравнения равновесия для моментов
Решение уравнений равновесия
Проверка правильности решения
Второй способ решения
🌟 Видео

Видео:Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Задача

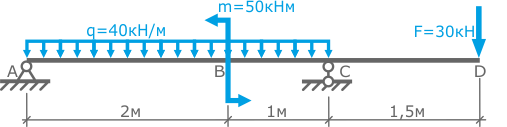
Для заданной двухопорной балки с консольной частью, нагруженной комплексом нагрузок: силой F, моментом m и распределенной нагрузкой q, определить величину и направление опорных реакций.

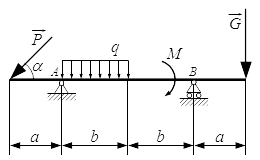
Расчетная схема балки показана на рис.1

Длина пролета балки 3м. Длина консольной части – 1,5м.

Видео:Определение реакций опор простой рамыСкачать

Пример решения

Рекомендуем посмотреть наш видеоурок. В нем мы постарались подробно показать порядок расчета реакций в опорах балки.

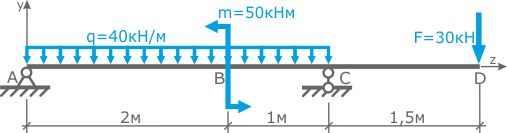
Для решения задачи, обозначим характерные точки (сечения) балки (точки A, B, C и D) и определим положение системы координат y-z, выбрав ее начало например в т. A (рис.2)

Обе опоры балки являются шарнирными, поэтому в каждой из них будет возникать только сила, обозначим их соответственно R_A и R_C

Так как все заданные нагрузки раположены исключительно в вертикальной плоскости (плоский поперечный изгиб) и не дают проекций на ось z, то опорные реакции будут тоже только вертикальными.

Вообще говоря, реакции в опорах являются такими силами, которые необходимы для удержания балки с приложенными к ней нагрузками, в статичном (неподвижном) состоянии. В данном случае эти силы не позволяют ей вращаться и перемещаться в вертикальной плоскости.

Данная балка является статически определимой, т.к. уравнений равновесия достаточно для определения неизвестных усилий в опорах балки.

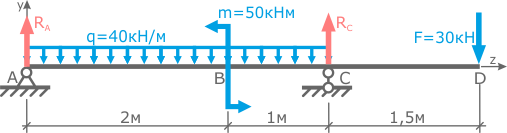
Для составления уравнений статики, опорные реакции R_A и R_C предварительно направляются произвольно, например, вверх (рис.3).

Для определения двух неизвестных реакций потребуется два уравнения.

Балка не перемещается по вертикали, т.е. сумма проекций всех сил на ось y равна нулю:

Здесь сумму моментов лучше записывать относительно точки расположенной на опоре (например, A), т.к. в этом случае соответствующая реакция R_A в уравнении не участвует.

Из выражения (2) определяем R_C:

и подставив его в выражение (1) находим R_A:

Направление и величина реакций, как правило, необходимы для дальнейших расчетов балки на прочность и жесткость, поэтому во избежание возможных ошибок рекомендуется выполнять проверку найденных значений.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Определение реакций опор в балке. Сопромат.Скачать

Как определить реакции в опорах?

Привет! В этой статье, предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции в опорах, и этому уделяют особое внимание на термехе. А курс термеха, по традиции, читают до сопромата. Для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.

Видео:Видеоурок 2. Определение реакций двухопорных балок.Скачать

Что такое реакция опоры?

Реакция опоры – это та сила, которая возникает в опоре от действия внешней нагрузки. В зависимости от конструкции опоры и ее назначения, в ней может появляться разное количество реакций, это может быть как сила, так и момент.

В начале этой статьи, расскажу о том, что должен уже уметь читатель, для успешного освоения данного урока. Если у Вас есть проблемы по поднятым вопросам на старте статьи, переходите по ссылкам на другие материалы на нашем сайте, после чего возвращайтесь к нам на чай реакции. Во второй части статьи, посмотрим, как вычисляются реакции на простейшем примере – балки, загруженной по центру сосредоточенной силой. Тут я покажу, как пользоваться уравнениями равновесия статики, как их правильно составлять. Дальше по плану, научу учитывать распределенную нагрузку, на примере той же балки. И завершать данный урок, будет пример определения реакций для плоской рамы, загруженной всевозможными типами нагрузок. Где применим уже все фишки, о которых я буду рассказывать по ходу урока. Что же, давайте начнем разбираться с реакциями!

Что вы должны уже уметь?

В этом блоке статье, я расскажу, как и обещал, что Вы должны УЖЕ уметь, чтобы понять то, что я буду докладывать дальше, про реакции опор.

Должны уметь находить сумму проекций сил

Да, это то, что Вам когда-то рассказывали на термехе, как собственно, и опорные реакции. Если Вы шарите немного в этих проекциях, то можете смело переходить к следующему пункту. Если же нет, то специально на этот случай, у меня есть другая статья, про проекции сил. Переходите, просвещайтесь, после чего, обязательно, возвращайтесь сюда!

Должны уметь составлять сумму моментов относительно точки

Немного теории! Познакомимся для начала с самим понятием момент силы. Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр. Проиллюстрирую написанное:

На изображении показано, как определить момент силы F, относительно точки O.

Так же, для моментов, нужно задаться каким-то правилом знаков. Сила относительно точки может поворачивать как по часовой стрелке, так и против нее. Я в своих уроках буду придерживаться такого правила:

Если сила относительно точки крутит ПРОТИВ часовой стрелке, то момент положительный.
Если она крутит ПО часовой стрелки, то соответственно момент отрицательный.

Причем, это правило условно! Какое правило Вы будете использовать совсем не важно, результат получите тот же самый. В теоретической механике, к примеру, делают также как я рассказываю.

Должны разбираться в основных видах опор

Теперь поговорим о самих опорах. В этой статье, будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

Шарнирно-подвижная опора препятствует вертикальному перемещению элементу конструкции, в связи с чем, в ней, под действием внешней нагрузки возникает вертикальная реакция. Обозначают ее обычно как R_i, где i — точка крепления опоры.

Шарнирно-неподвижная опора имеет две реакции: вертикальную и горизонтальную. Так как препятствует перемещению в этих двух направлениях.

Вообще-то способов закрепления элементов конструкций и их условных обозначений достаточно много, но в рамках этой статьи их рассматривать не будем.

Видео:Определение реакций двухопорной балкиСкачать

Примеры определения сил реакций опор

Вроде, всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнем с простейшей расчетной схемы балки.

Определение реакций опор для балки

Возьмем балку на двух опорах, длиной 2 метра. Загрузим ее, посередине пролета, сосредоточенной силой:

Для этой расчетной схемы, выгодно записать такое условие равновесия:
То есть, будем составлять две суммы моментов относительно опорных точек, из которых можно сразу выразить реакции в опорах. В шарнирно-неподвижной опоре горизонтальная реакция будет равна нулю, ввиду того, что горизонтальные силы отсутствуют. Последним уравнением, взяв сумму проекций на вертикальную ось, сможем проверить правильность нахождения опорных реакций, это сумма должна быть равна нулю.

Введем систему координат, пустим ось х вдоль балки, а ось y вертикально. Обозначим реакции в опорах как R_A и R_B:

Запишем уравнение моментов, относительно точки А. Сила F поворачивает ПО часовой стрелки, записываем ее со знаком МИНУС и умножаем на плечо. Сила R_B поворачивает ПРОТИВ часовой стрелки, пишем ее со знаком ПЛЮС и умножаем на плечо. Все это приравниваем к нулю:

Из полученного уравнения выражаем реакцию R_B.

Первая реакция найдена! Вторая реакция находится аналогично, только теперь уравнение моментов записываем относительно другой точки:

После нахождения реакций, делаем проверку:

Определение реакций опор для балки с распределенной нагрузкой

Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно свернуть до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:

Определение опорных реакций для плоской рамы

Теперь, после освоения азов по расчету реакций, предлагаю выполнить расчет плоской рамы. Для примера, возьмем раму, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:

заменяем опоры на реакции;
сворачиваем распределенную нагрузку до сосредоточенной силы;
вводим глобальную систему координат x и y.

Для такой расчетной схемы, лучше использовать следующую форму условий равновесия:

Составив первое уравнение, относительно точки A, сразу найдем реакцию в опоре B:

Записав второе уравнение, сумму проекций на ось х, найдем горизонтальную реакцию H_A:

И, наконец, третье уравнение, позволит найти реакцию R_A:

Не пугайтесь отрицательного значения реакции! Это значит, что при отбрасывании опоры, мы не угадали с направлением этой силы.

Расчет же показал, что R_A, направленна в другую сторону:

В итоге, получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумму будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!

На этом заканчиваю данный урок. Если у Вас остались какие-то вопросы по нахождению опорных реакций, смело задавайте их в комментариях к этой статье. Обязательно на все отвечу!

Спасибо за внимание! Если понравилась данная статья, расскажите о ней своим одногруппникам, не жадничайте 🙂

Также рекомендую подписаться на наши соц. сети, чтобы быть в курсе обновлений материалов проекта.

Видео:Определение опорных реакций балки на двух опорахСкачать

Определение реакций опор балки – решение задачи

Видео:РГЗ 2 Статика Балочные системы Определение реакций в опорахСкачать

Как определить реакции опор балки

Видео:Определение реакций опор простой рамыСкачать

Пример решения задачи на определение реакций опор балки

Жесткая балка, линейные размеры которой указаны на рисунке 1, закреплена в точках А и В. На балку действуют пара сил с моментом М, равномерно распределенная нагрузка интенсивностью q и две силы P и G, место приложения которых показано на рисунке.
Определить реакции опор балки в точках A и B, вызываемые указанными нагрузками.

Дано:
P = 20,2 Н ; G = 22,6 Н ; q = 2 Н/м ; M = 42,8 Н·м ; a = 1,3 м ; b = 3,9 м ; α = 45° ;

Решение задачи

Проводим оси x и y системы координат. Начало системы координат поместим в точку A . Ось x направим горизонтально, вдоль балки. Ось y – вертикально. Ось z перпендикулярна плоскости рисунка и направлена на нас. На рисунке она не указана.

Силы, действующие на балку.

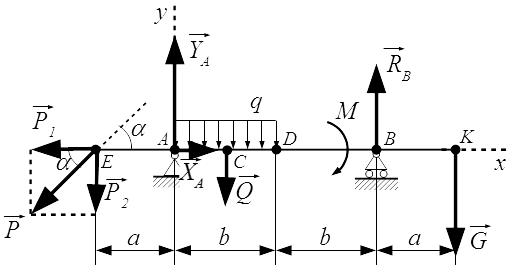
Отбрасываем опоры и заменяем их силами реакций.
В шарнире A , разложим силу реакции на составляющие и вдоль осей координат.
Реакция , в подвижной опоре на катках, направлена вертикально. Предполагаемые направления реакций опор выбираем по своему усмотрению, наугад. Если ошибемся с направлением реакции, то получим отрицательное значение, что будет говорить о том, что соответствующая сила реакции направлена в противоположную сторону.

Заменим равномерно распределенную нагрузку q равнодействующей . Абсолютное значение равнодействующей равно площади эпюры:
Н .
Точка приложения равнодействующей находится в центре тяжести эпюры. Поскольку эпюра представляет собой прямоугольник, то ее центр тяжести находится в точке C – посередине отрезка AD :
AC = CD = b/2 = 1,95 м .

Уравнения равновесия для сил

Определяем проекции сил на оси координат.

Разложим силу на составляющие вдоль координатных осей:
.
Абсолютные значения составляющих:
.
Вектор параллелен оси x и направлен в противоположную от нее сторону. Вектор параллелен оси y и также направлен в противоположную сторону. Поэтому проекции силы на оси координат имеют следующие значения:
.

Остальные силы параллельны осям координат. Поэтому они имеют следующие проекции:
;
;
;
;
.

Составляем уравнения равновесия для сил.
Сумма проекций всех сил на ось x равна нулю:
;
;
;
(П1) .

Сумма проекций всех сил на ось y равна нулю:
;
;
;
(П2) .

Уравнения равновесия для моментов

Итак, мы уже составили два уравнения для сил: (П1) и (П2). Но в них есть три неизвестные величины: , и . Чтобы их определить, нам нужно составить еще одно уравнение.

Составим уравнение равновесия для моментов сил. Для этого нам нужно выбрать ось, относительно которой мы будем вычислять моменты. В качестве такой оси возьмем ось, проходящую через точку A , перпендикулярно плоскости рисунка. За положительное направление выберем то, которое направлено на нас. Тогда, по правилу правого винта, положительным направлением закручивания будет направление против часовой стрелки.

Находим моменты сил относительно выбранной оси.
Силы , и пересекают ось. Поэтому их моменты равны нулю:
; ; .

Сила перпендикулярна плечу AB . Ее момент:
.
Поскольку, относительно оси A , сила направлена против часовой стрелки, то ее момент положительный.

Сила перпендикулярна плечу AK . Поскольку, относительно оси A , эта сила направлена по часовой стрелки, то ее момент имеет отрицательное значение:
.

Аналогичным способом находим моменты остальных сил:
;
.
Момент от пары сил M не зависит от точек приложения сил, входящих в пару:
.

Составляем уравнение равновесия. Сумма моментов сил относительно оси A равна нулю:
;

;
;
(П3) .

Решение уравнений равновесия

Итак, для трех неизвестных величин, мы получили три уравнения:
(П1) .
(П2) .
(П3) .

Решаем эти уравнения. Вычисляем расстояния.
м;
м;
м;
м.

Из уравнения (П1) находим:
Н.
Из уравнения (П3) находим:

Н.
Из уравнения (П2) имеем:
Н.
Абсолютное значение реакции опоры в точке A :
Н.

Проверка правильности решения

Чтобы проверить, правильно ли мы определили реакции опор балки, найдем сумму моментов сил относительно другой оси. Если мы нашли реакции правильно, то она должна равняться нулю.

Возьмем ось, проходящую через точку E . Вычисляем сумму моментов сил относительно этой оси:

.
Найдем погрешность вычисления суммы моментов. Найденные силы мы округлили до двух знаков после запятой. То есть погрешность определения реакций опор составляет 0,01 Н . Расстояния, по порядку величины, примерно равны 10 м. Тогда погрешность вычисления суммы моментов составляет около 10·0,01 = 0,1 Нм . Мы получили значение -0,03 Нм . Эта величина отличается от нуля не более, чем на величину погрешности. То есть, с учетом погрешности вычислений, сумма моментов относительно другой оси равна нулю. Значит решение правильное, силы реакций найдены верно.

Второй способ решения

Первым способом мы составили два уравнения для сил и одно – для моментов. Задачу можно решить другим способом, составив два уравнения для моментов и одно для сил.

Воспользуемся тем, что сумма моментов сил равна нулю относительно любой оси. Возьмем вторую ось, которая проходит через точку B перпендикулярно плоскости рисунка. Сумма моментов сил относительно этой равна нулю:
.
Вычисляем моменты сил относительно оси B .
; ; ;
;
;
;
;
.

Сумма моментов сил относительно оси B равна нулю:
;

;
;
(П4) ;

Итак, вторым способом, мы также имеем три уравнения:
(П1) .
(П3) ;
(П4) .

Здесь каждое уравнение содержит только одну неизвестную величину. Реакции и определяются из тех же уравнений, что и ранее. Находим силу из уравнения (П4):

Н.

Значение реакции совпало со значением, полученным первым способом из уравнения (П2).

Автор: Олег Одинцов . Опубликовано: 14-10-2017 Изменено: 28-12-2021