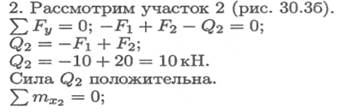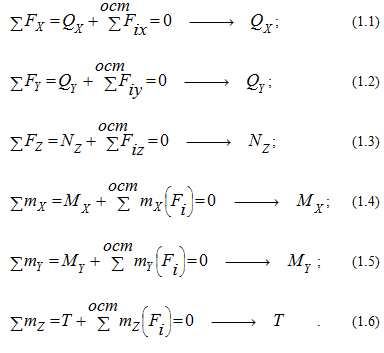Запишите систему уравнений используемую при определении внутренних силовых факторов

Видео:БАЛКА - 90 СТУДЕНТОВ САМОСТОЯТЕЛЬНО СТРОЯТ ЭПЮРЫ после просмотра этого видео!Скачать

Метод сечений и внутренние силовые факторы (ВСФ)

Прочность твердого тела обусловлена силами сцепления между отдельными его частицами (атомами, молекулами и т. п.). В случае нагружения твердого тела внешней нагрузкой (активными и реактивными силами) внутренние силы сцепления изменяются. При этом появляются дополнительные внутренние силы, сопровождающие деформацию тела. Именно эти дополнительные внутренние силы и являются предметом изучения в курсе сопротивления материалов. По мере возрастания внешней нагрузки увеличиваются и внутренние силы, но лишь до определенного предела, при превышении которого наступает разрушение.

Для решения задач сопротивления материалов очень важно уметь определять внутренние силы и деформации стержня. При определении внутренних сил в каком-либо сечении стержня используют метод сечений.

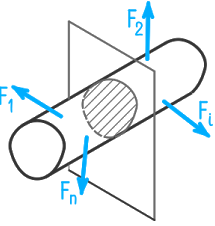
Рассмотрим на конкретном примере сущность метода сечений. Возьмем стержень, находящийся в состоянии равновесия под действием сил Ft, F₂, F_> и F₄ (рис. 3,а). Для определения внутренних сил, действующих в произвольном сечении А, мысленно рассечем стержень и отбросим одну из двух полученных частей, например, правую. Тогда на оставшуюся левую часть стержня будут действовать внешние силы F и F₂.

Рис. 3. Метод сечений: а) стержень, рассеченный плоскостью;

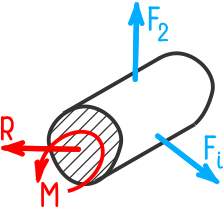
б) левая отсеченная часть стержня

Для того чтобы эта часть стержня оставалась в равновесии, следует действие отброшенной правой части стержня на оставшуюся левую часть заменить внутренними силами, приложенными по всему сечению (рис. 3, б).

Являясь внутренними силами для целого стержня, эти силы играют роль внешних сил для его левой части.

NB: в дальнейшем силы, возникающие в сечении, будем называть внутренними и в то же время на рисунках изображать их в виде внешних сил.

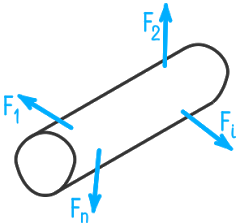
Распределенные по сечению внутренние силы образуют пространственную систему сил и приводятся к статически эквивалентным им обобщенным усилиям — главному вектору и главному моменту М_гл (рис. 4, а).

В сопротивлении материалов, характеризуя усилия в стержне, обычно рассматривают поперечные сечения, а обобщенные усилия представляют в главной координатной системе (при этом ось z направляют по нормали к сечению, а оси х и у располагают в плоскости сечения).

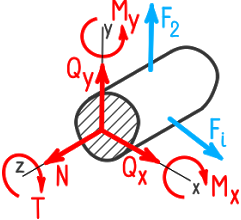
Проецируя главный вектор /?_г, на оси координат, получаем три его составляющие: N_y Q_y и Q_x. Проекциями главного момента на координатные оси являются его составляющие: моменты М_х, М_у и Г, каждый из которых стремится повернуть отсеченную часть стержня вокруг одной из координатных осей. Эти составляющие главного вектора и главного момента на координатные оси называют внутренними силовыми факторами (рис. 4, б).

Рис. 4. Метод сечений: а) приведение системы внутренних сил в сечении к главному вектору и главному моменту; б) разложение главного вектора и главного момента на координатные оси

Внутренними силовыми факторами называются проекции главного вектора и главного момента всех внутренних сил, возникающих в поперечном сечении стержня, на главные координаты оси, помещаемые обычно в центр тяжести сечения.

В общем случае нагружения стержня в его поперечном сечении могут возникать шесть внутренних силовых факторов, которые имеют следующие названия:

S N — продольная (нормальная) сила;

S Т — крутящий момент.

При известных внешних силах все шесть внутренних силовых факторов могут быть определены из шести уравнений статики (уравнений равновесия), которые составляются для отсеченной части стержня (правой или левой):

NB: в приведенных условиях равновесия отсеченной части стержня символами F_x omc , F_y omc и F_z ome обозначены проекции внешних сил на соответствующие координатные оси; а символом F° mc — внешние силы.

Рассмотренный метод сечений позволяет перевести внутренние силовые факторы в категорию внешних сил и, подчинив условиям равновесия, определить их величины и направления.

Сущность метода сечений заключается в следующих четырех действиях:

• 1. Рассечь мысленно стержень плоскостью, перпендикулярной его оси в том месте, где требуется найти внутренние силовые факторы (см. рис. 3, а).
• 2. Отбросить одну из частей стержня (правую или левую).
• 3. Заменить действие отброшенной части стержня на оставленную часть искомыми внутренними силовыми факторами (см. рис. 4, б). Равновесие оставленной части не нарушится лишь в том случае, если к ней приложить ВСФ, заменяющие действие отброшенной части. Для оставленной части они будут играть роль внешних сил (см. рис. 3, б).
• 4. Уравновесить оставленную часть стержня и из условий равновесия оставленной части стержня найти величины и направления внутренних силовых факторов.

От степени усвоения метода сечений зависит успешное изучение и понимание основных вопросов сопротивления материалов. Добиться этого несложно, если при применении метода сечений каждый раз последовательно использовать все четыре указанные операции. При этом следует помнить, что пропуск какой-либо из этих операций неизбежно приведет к ошибкам и недопониманию изучаемого вопроса.

При применении метода сечений должны быть предварительно определены все внешние силы и моменты, приложенные к отсеченной части стержня, в том числе и опорные реакции. Оставленная часть стержня должна рассматриваться как свободное тело, находящееся под действием приложенных к нему внешних сил, моментов и внутренних силовых факторов, не изменяющее своего положения в пространстве (опоры отсутствуют, так как их действия заменены опорными реакциями).

Видео:Построение эпюр в балке ( Q и M ). СопроматСкачать

Определение внутренних силовых факторов

Тема 2.6. Изгиб.

Построение эпюр поперечных сил

И изгибающих моментов.

Основные правила построения эпюр

Знать порядок построения и контроля эпюр поперечных сил и изгибающих моментов.

Уметь строить эпюры поперечных сил и изгибающих моментов.

Эпюры поперечных сил и изгибающих моментов можно строить, предварительно разделив балку на участки нагружения и составляя уравнения, выражающие изменения Q и М_х по участкам.

Напомним, что границы участков нагружения — это сечения, в которых приложены внешние нагрузки.

Примеры решения задач

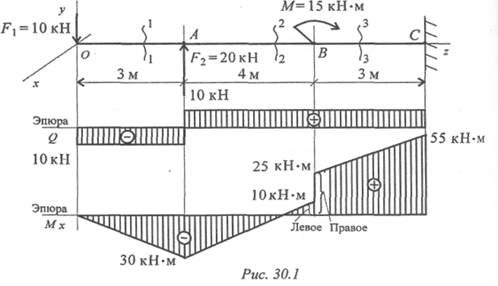
Пример 1.На балку действуют сосредоточенные силы и мо­мент (рис. 30.1). Построить эпюры поперечных сил и изгибающих моментов.

Тема 2.6. Изгиб 247

Решение

Последовательно по участкам нагружения рассматриваем вну­тренние силовые факторы в сечениях. Силовые факторы определяем из условий равновесия отсеченной части. Для каждого участка за­писываем уравнения внутренних силовых факторов.

Используем известные правила:

— поперечная сила численно равна алгебраической сумме проекций внешних сил на ось Оу;

— изгибающий момент численно равен алгебраической сумме
моментов внешних сил, действующих на отсеченную часть, относительно нейтральной оси, совпадающей с осью Ох;

— принятые знаки поперечных сил и изгибающих моментов
(рис. 30.2):

Составим уравнения равновесия.

1. Рассмотрим участок 1 (рис. 30.3а).

Изгибающий момент меняется по линейному закону, график -прямая линия.

Поперечную силу и изгибающий момент можно определять сра­зу из зависимостей Q_y = ΣFy; М_х = Σmх, не составляя уравнения равновесия участка.

Знак каждого из слагаемых этих уравнений определяем от­дельно (участок 3).

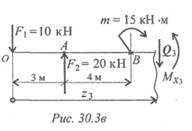
3. Рассмотрим участок 3 (рис. 30.3в).

Qз = -10 + 20 = 10 кН — поло­жительна.

MxB справа = — 10·7+20·4+15 = 25 кН · М;

Обращаем внимание, что для точки В получено два значения изгибающих моментов: из уравнения для участка 2 левее точки В и из уравнения для участка 3 — правее точки В.

Это объясняется тем, что именно в этой точке приложен внеш­ний момент и поэтому внутренний момент сил упругости меняется.

В точках приложения внешнего момента на эпюре моментов по­явится скачок, равный величине приложенного момента.

Поперечная сила в точке В для второго и третьего участков одинакова. Следовательно, приложение внешнего момента не от­ражается на эпюре поперечных сил. График поперечной силы на участке 3 — прямая линия.

График изменения изгибающих моментов на третьем участке также прямая линия.

Тема 2.6. Изгиб 249

4. Построение эпюр. Порядок построения эпюр остается преж­ним: масштабы эпюр выбираются отдельно, исходя из значений мак­симальных сил и моментов.

Графики обводятся толстой основной линией и заштриховыва­ются поперек. На графиках указываются значения поперечных сил, изгибающих моментов и единицы измерения.

Правила построения эпюр (рис. 30.1 и 30.4):

1. Для участка, где отсутствует распределенная нагрузка, попе­речная сила постоянна, а изгибающий момент меняется по линейно­му закону.

2. В частном случае, когда поперечная сила на участке равна ну­лю, изгибающий момент постоянен (чистый изгиб), график — пря­мая линия, параллельная продольной оси (на рис. 30.1 отсутствует).

3. В том месте, где к балке приложена внешняя сосредоточенная сила, на эпюре Q возникает скачок на величину приложенной силы, а на эпюре моментов — излом.

4. В сечении, где к балке приложена пара сил (сосредоточенный момент), на эпюре М_и возникает скачок на величину момента этой пары. Поперечная сила при этом не изменяется.

5. В сечении на конце балки поперечная сила равна приложенной в этом сечении сосредоточенной силе или реакции в заделке.

6. На свободном конце балки или шарнирно опертом конце мо­мент равен нулю, за исключением случаев, когда в этом сечении приложена пара сил (внешний момент).

Пример 2.На двухопорную балку действуют сосредоточенные силы и моменты (рис. 30.4). Построить эпюры поперечных сил и изгибающих моментов.

Для двухопорной балки построение эпюр начинают с определе­ния опорных реакций балки. Для их определения используем систему уравнений равновесия, составляем два уравнения моментов относи­тельно шарнирных опор. Затем проводим проверку правильности решения по уравнению

Σ Fky = 0 (см. лекцию 6).

Решение

1. Определение реакций в опорах. Уравнения равновесия:

Реакция в опоре направлена в обратную сторону.

Проверка: ΣFy = 0;

Реакции определены верно.

2. Для упрощения расчетов при построении эпюр поперечных сил и изгибающих моментов можно провести расчет по характерным точкам без составления уравнений.

Для этого используют известные связи между поперечной силой и изгибающим моментом и правила построения эпюр.-

Участок 1 (от точки А до точки С).

Тема 2.6. Изгиб 251

В точке А приложена реакция Ra, направленная вниз. Попереч­ная сила на участке постоянна: Q1 = Ra = — З6кН.

Момент в точке А равен нулю.

Точка С (слева). Приложена внешняя сила F1 = З5кН, напра­вленная вверх, — здесь возникнет скачок вверх на величину З5кН. Момент в точке С (слева) может быть рассчитан по известной зави­симости МС слева =-R_A · 6; МС слева =-36·6 =-216 кН· м.

Участок 2 (от точки С справа до точки В).

Поперечная сила в точке С (справа) равна Qc = -Ra + F1; Q_c = -36 + 35 = -1кН.

В точке С приложена внешняя пара сил с моментом 80кН·м, следовательно, здесь проявляется скачок на величину приложенного момента: Мc справа = МС слева + m; Мc справа = -216 + 80 = 136кН·м.

Поперечная сила на втором участке постоянна: Q2 = Qc справа .

Момент в точке В определяется по зависимости

МB = -R_A • 10 + F1 • 4 + m; M_B = -36 • 10 + 35 • 4 + 80 = -140 кН•м.

Справа и слева от точки В момент имеет одинаковые значения.

Участок 3 (от точки В (справа) до точки D).

В точке В приложена внешняя сила Rb. Здесь появляется скачок на величину 71 кН, Q_B = -1 + 71 = 70 кН.

Дальше по участку поперечная сила не изменяется. Момент в точке D равен нулю, т.к. здесь не приложена внешняя пара сил: M_D = 0.

Рассмотрение поперечных сил и изгибающих моментов можно было провести и справа налево.

По полученным значениям сил и моментов строим эпюры (эпю­ры под схемой вала, рис. 30.4).

Контрольные вопросы и задания

1. Определите величины поперечных сил в сечении 1 и в сечении 2 (рис. 30.5).

2. Напишите формулу для расчета изгибающего момента в сечении 3 (рис. 30.6).

3. Из представленных эпюр выберете эпюру поперечной силы для изображенной балки (рис. 30.7).

A. Обратить внимание на знак силы в сечении 1 (знак +).

Б. Обратить внимание на величину скачков в местах приложе­ния внешних сил.

B. Приложение момента пары сил не должно отражаться на
эпюре Q.

4. По рис. 30.8 выбрать эпюру изгибающего момента для изображенной на рис. 30.7 балки.

A. На конце бруса приложен момент пары, следовательно, в этом
месте изгибающий момент должен быть равен этому же значению.

Б. Обратить внимание на знак момента в сечении 1.

B. В точке А приложена также и сила , поэтому линия , очертившая

Тема 2.6. Изгиб 253

эпюру, должна быть наклонной.

5. Ответьте на вопросы тестового задания.

Тема 2.6. Изгиб.

Определение внутренних силовых факторов

Видео:СМ -1.7 Метод сечений, внутренние силовые факторы (ВСФ)Скачать

iSopromat.ru

Внутренние силовые факторы (усилия) возникают в результате деформации бруса, когда под действием внешних нагрузок происходит изменение взаимного расположения элементарных частиц тела.

По своей природе внутренние силовые факторы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций. Для определения этих усилий применяют метод сечений:

надо мысленно рассечь брус, находящийся в равновесии, на две части

и рассмотреть равновесие одной из них.

Действие усилий отброшенной части бруса заменим уравновешивающими рассматриваемую часть внутренней силой R и внутренним моментом M.

Для упрощения расчетов силу R и момент M принято раскладывать на составляющие усилия относительно осей координат x, y и z.

Таким образом, под действием внешних нагрузок в поперечном сечении бруса могут возникать следующие внутренние силовые факторы:

• N_z = N — продольная растягивающая (сжимающая) сила;
• M_z = T — крутящий (скручивающий) момент;
• Q_x (Q_y) = Q — поперечные силы;
• M_x (M_y) = M — изгибающие моменты.

Каждый внутренний силовой фактор определяется из соответствующего уравнения равновесия оставшейся после рассечения бруса части (уравнения статики):

Наш видеоурок построения эпюр внутренних силовых факторов для балки:

Видео:Лекция по сопротивлению материалов № 1. Введение, внутренние силовые факторы, метод сечений.Скачать

Правила знаков для внутренних силовых факторов

Для определения знаков внутренних усилий, возникающих в брусе при различных способах его нагружения, приняты следующие правила:

• при растяжении/сжатии — положительными являются растягивающие усилия;
• при кручении — положительны моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки;
• при изгибе — положительны моменты сжимающие верхний слой балки.

Видео:Решение систем уравнений методом подстановкиСкачать

Эпюры внутренних силовых факторов

В инженерной практике особое место занимает умение ясно представить взаимодействие усилий в конструкции, а также связь между внешними и внутренними силами в элементах конструкции, для этого графически изображают внутренние силовые факторы в функции осевой координаты и называют эти графики — эпюрами.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

🌟 Видео

1 14 Плоская рама Построение эпюр внутренних силовых факторовСкачать

4. Построение эпюр в раме ( практический курс по сопромату )Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Mathcad. Расчет внутренних силовых факторов вертикально нагруженной балки.Скачать

Решение систем уравнений второго порядка. 8 класс.Скачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Решение систем уравнений. Методом подстановки. Выразить YСкачать

Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

Сопротивление материалов/ Изгиб. Определение опорных реакций, построение эпюр Q и M. (Перезапись)Скачать

Рама. Построение эпюр N, Q, M.Скачать

Классификация четырехполюсников. Системы уравнений четырехполюсниковСкачать

ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать