Запиши уравнение данной параболы ответ y 2 x ответить (5 видео)

Парабола, график, вершина, нули.

Содержание

теория по математике 📈 функции
Пример №1
Пример №2
Пример №3
Пример №4
Функция y=x² и её график. Парабола
График функции y=x²
Свойства параболы y=x²
Дана парабола у = (х — 2)2. а) Определите координаты вершины параболы. б) Запишите уравнение оси симметрии параболы. в) Какова область определения функции?
Ваш ответ
решение вопроса
Похожие вопросы
🎦 Видео

теория по математике 📈 функции

Функция вида y=ax 2 +bx+c, где а, b, с – некоторые числа, причем, а ≠ 0 число, х – переменная, называется квадратичной функцией.

Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.

Чтобы найти координаты вершины параболы (х₀; у₀), надо воспользоваться формулой:

для нахождения у₀ можно просто подставить значение х₀ в формулу данной функции y₀=ax 2 +bx+c вместо х.

Рассмотрим это на примере конкретно заданной функции.

Пример №1

Найти вершину параболы, заданной формулой у=2х 2 – 8х + 5.

Найдем, чему равны коэффициенты: а=2; b= – 8

Подставим их в формулу и вычислим значение х₀:

х₀= − b 2 a . . = 8 2 ∙ 2 . . = 8 4 . . = 2

Теперь в заданную по условию формулу вместо х подставим найденное значение у₀=2 ∙ 2 2 – 8 ∙ 2 + 5=8 – 16 + 5= –3

Итак, мы нашли координаты вершины параболы: (2; –3).

Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.

Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.

Пример №2

Найти нули функции у=х 2 +4х – 5

Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х 2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:

D=b 2 – 4ac=4 2 – 4 ∙ 1 ∙ ( − 5 ) = 36

Значит, нули функции равны –5 и 1

Примечание к заданию по нахождению нулей функции без графика

Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).

Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.

Пример №3

Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.

Теперь можно выполнить соответствие:

А	Б	В
2	3	1

Пример №4

Рассмотрим еще пример на соответствие

В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х₀.

Итак, найдем х₀ для формулы «Б»:

х₀= − b 2 a . . = − 4 2 ∙ 2 . . = − 4 4 . . = − 1

Видим, что х₀ отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.

Запишем в таблицу

А	Б	В
2	3	1

А) a>0, с >0 Б) а 0 В) а>0, с

На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a 0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с 0, с >0 – это график №1

Б) а 0 – это график №3

pазбирался: Даниил Романович | обсудить разбор | оценить

Установите соответствие между функциями и их графиками.

ФУНКЦИИ

Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х 2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.

Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3

pазбирался: Даниил Романович | обсудить разбор | оценить

На рисунках изображены графики функций вида

Установите соответствие между знаками коэффициентов a и c и графиками функций.

Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида

Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a 0.

Далее мы смотрим, на что влияет коэффициент c.

Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:

если c > 0, то вершина параболы расположена выше оси х

Из всего вышеперечисленного можно найти ответ:

pазбирался: Даниил Романович | обсудить разбор | оценить

Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

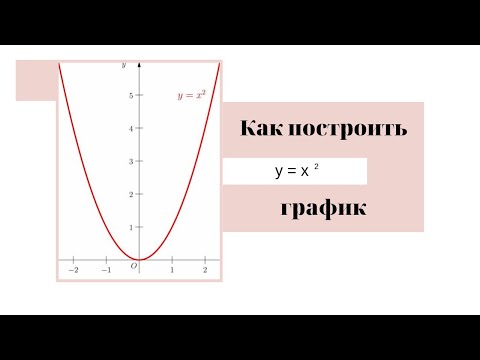
Функция y=x² и её график. Парабола

График функции y=x²

Составим таблицу для расчёта значений функции $y = x^2$:

Отметим полученные точки на координатной плоскости и соединим их кривой:

Полученный график называют параболой. Точка (0;0) — это вершина параболы. Вершина делит график на левую и правую части, которые называют ветвями параболы.

Свойства параболы y=x²

1. Область определения $x in (- infty;+ infty)$ — все действительные числа.

2. Область значений $y in [0;+ infty)$ — все неотрицательные действительные числа.

3. Функция убывает при $x lt 0$, функция возрастает при $x gt 0$.

4. Наименьшее значение функции y = 0 — в вершине параболы при x = 0. Вершина параболы совпадает с началом координат.

5. Все точки на ветвях параболы лежат выше оси абсцисс, для них $y gt 0$.

6. График параболы симметричен относительно оси ординат, противоположным значениям аргумента соответствует одно и то же значение функции:

$$ (-x)^2 = x^2 Rightarrow y(-x) = y(x) $$

В таких случаях говорят, что функция чётная.

Если использовать запись для множеств и их элементов (см.§8 данного справочника), то область определения можно записать как $$, а область значений $$.

Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать