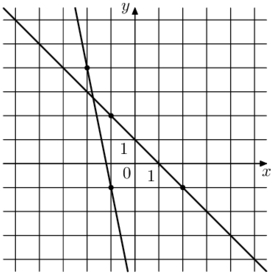
На рисунке изображён графики двух линейных функций. Найдите ординату точки пересечения графиков.
На рисунке изображены прямые, линейных функции имеют вид:
Найдём k и b функции:
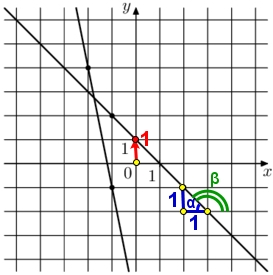
k – тангенс угла ( β ) наклона прямой, по отношению к оси х. Тангенс – это отношение противолежащего катета, к прилежащему катету. Тангенсы смежных углов равны по модулю, но противоположны по знаку.
Найдём тангенс угла α , смежного к искомому углу:
b – сдвиг прямой по оси у, по графику видим, прямая сдвинута от 0 на 1 .
b = 1
Функции имеет вид:
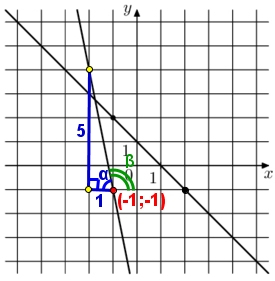
Найдём k и b функции:
Подставим координаты точки (–1;–1), принадлежащие прямой и k = –5, найдём b :
–1 = –5·(–1) + b
–1 – 5 = b
b = –6
Функция имеет вид:
y = –5x – 6
В точке пересечения прямых значения функций (y) равны, найдём абсциссу (х) точки пересечения:
–1·x + 1 = –5x – 6
–x + 5x = –6 – 1
4x = –7
Подставим значение х = –1,75, в любое уравнение и найдём ординату (y) точки пересечения прямых:
y = –1·(–1,75) + 1 = 2,75
Взаимное расположение графиков квадратных трёхчленов
Расположение графика квадратного трёхчлена относительно осей координат
В §28 данного справочника мы показали, что квадратный трёхчлен можно представить в виде:
- ось симметрии $x = -frac$
- вершину параболы на оси симметрии $(–frac; -frac)$
- точку пересечения (0;c) с осью OY
Любая парабола $y = ax^2+bx+c, a ≠ 0$ пересекается с осью OY в единственной точке (0;c) .
Количество точек пересечения параболы $y = ax^2+bx+c$ с осью OX зависит от знака дискриминанта.
Если $D gt 0$ , парабола имеет две точки пересечения с $x_1,2 = frac<-b pm sqrt>$ на оси OX.
Если D = 0 , парабола имеет одну точку пересечения $x_0 = -frac$, которая лежит на оси OX и является вершиной параболы.
Если $D lt 0$ у параболы нет ни одной точки пересечения с осью OX.
Видео:Точки пересечения графиков линейных функций. 7 класс.ОбразовательныйСкачать

Точки пересечения параболы с осью OX






Точки пересечения двух парабол
На практике часто возникает задача «перехвата» одного тела другим, т.е. поиска точек пересечения двух траекторий; а тела в поле тяготения Земли нередко движутся по параболе.
Поэтому исследовать возможные точки пересечения двух парабол – важная прикладная задача. Пусть уравнения парабол:
$$ y = a_1 x^2+b_1 x+c_1, quad y = a_2 x^2+b_2 x+c_2 $$
В точках пересечения выполняется равенство:
$$ a_1 x^2+b_1 x+c_1 = a_2 x^2+b_2 x+c_2 $$
$$ (a_1-a_2 ) x^2+(b_1-b_2 )x+(c_1-c_2 ) = 0 $$
Если ввести обозначения $A = a_1-a_2, B = b_1-b_2, C = c_1-c_2$, получаем уравнение:
Количество решений этого уравнения в зависимости от нулевых и ненулевых значений параметров равно 11 и описывается схемой общего алгоритма решений квадратного уравнения (см.§25 данного справочника).
$ a_1 = a_2, b_1 = b_2, $
Две параболы совпадают
Бесконечное множество общих точек, $x in Bbb R$
$A = B = 0, C neq 0$
$ a_1 = a_2, b_1 = b_2, $
Параболы имеют вид
У них общая ось симметрии
$ x = -frac$, одна парабола находится над другой.
Ветки сходятся только на бесконечности.
Точек пересечения нет
$A = 0, B neq 0, C = 0$
$ a_1 = a_2, b_1 neq b_2 $
Параболы имеют вид
Обе проходят через точку (0;c).
Это – единственная точка пересечения.
Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Одна точка пересечения
$A = 0, B neq 0, C neq 0$
$ a_1 = a_2, b_1 neq b_2 $
Параболы имеют вид
Абсцисса точки пересечения
Одна точка пересечения (касание)
$A neq 0, B = 0, C = 0$
$ a_1 neq a_2, b_1 = b_2 $
Параболы имеют вид
Пересекаются при x=0 (точка касания)
Одна точка пересечения (касание) (0;c)
$A neq 0, B = 0, C neq 0$
$ a_1 neq a_2, b_1 = b_2 $
Параболы имеют вид
Не пересекаются, если
Две точки пересечения
Пересекаются в двух точках
Две точки пересечения
$A neq 0, B neq 0, C = 0$
$ a_1 neq a_2, b_1 neq b_2 $
Параболы имеют вид
$$ y = a_1 x^2+b_1 x+c $$
$$ y = a_2 x^2+b_2 x+c $$
Две точки пересечения
Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Две точки пересечения,
одна из которых (0;c)
$A neq 0, B neq 0, C neq 0$
$ a_1 neq a_2, b_1 neq b_2 $
Все параметры парабол разные
Две точки пересечения
Две точки пересечения
Одна точка пересечения (касание)
Одна точка пересечения
Точек пересечения нет
Точек пересечения нет
Если две параболы не совпадают, то они могут иметь 1) две точки пересечения; 2) одну точку пересечения; 3) ни одной точки пересечения.
Иметь ровно 3, 4, 5 и т.д. точек пересечения две параболы не могут!
Примеры
Пример 1. Найдите точки пересечения параболы с осями координат:
Пересечение с осью OY: $<left< begin x = 0 \ y = -1end right.>$
Пересечение с осью OX:
$$ 3x^2+2x-1 = 0 Rightarrow (3x-1)(x+1) = 0 Rightarrow $$
$ Rightarrow left[ begin <left< begin x = frac \ y = 0 end right.> \ <left< begin x = -1 \ y = 0 end right.> end right.$ — две точки пересечения
Пересечение с осью OY: $<left< begin x = 0 \ y = 1end right.>$
Пересечение с осью OX:
$$ -4x^2-3x+1 = 0 Rightarrow 4x^2+3x-1 = 0 $$
$$ (4x-1)(x+1) = 0 Rightarrow$$
$ Rightarrow left[ begin <left< begin x = frac \ y = 0 end right.> \ <left< begin x = -1 \ y = 0 end right.> end right.$ — две точки пересечения
Пересечение с осью OY: $<left< begin x = 0 \ y = 1end right.>$
Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Пересечение с осью OX:
$$ D = 2^2-4 cdot 5 cdot 1 = 4-20 = -16 lt 0 $$
Парабола не пересекает ось OX
Пересечение с осью OY: $<left< begin x = 0 \ y = -4end right.>$
Пересечение с осью OX:
$$ -x^2+4x-4 = 0 Rightarrow x^2-4x+4 = 0 Rightarrow $$
$$ Rightarrow (x-2)^2 = 0 Rightarrow <left< begin x = 2 \ y = 0 end right.>$$ — одна точка пересечения
Пример 2*. Даны две параболы
$$ y = 2x^2+5x+1 и y = x^2+3x+k $$
Найдите такое значение параметра k, чтобы параболы
1) имели две точки пересечения; 2) имели одну точку пересечения; 3) не пересекались.
$$ a_1 = 2, b_1 = 5, c_1 = 1, a_2 = 1, b_2 = 3, c_2 = k $$
$$ a_1 neq a_2, b_1 neq b_2 $$
A = 2-1 = 1, B = 5-3 = 2, C = 1-k
Нам необходимо рассмотреть 4 последних случая из представленных выше, в таблице §29.
1) Параболы имеют две точки пересечения в двух случаях:
1 случай: $c_2 = c_1$, k = 1
2 случай: $c_2 ≠ c_1, D gt 0$
$$ D = B^2-4AC = 2^2-4 cdot 1 cdot (1-k) = 4k gt 0 Rightarrow k gt 0 $$
Оба случая можем объединить требованием $k gt 0$.
2) Параболы имеют одну точку пересечения, если:
$$ D = 4k = 0 Rightarrow k = 0 $$
3) Параболы не имеют общих точек, если:
$$ D = 4k lt 0 Rightarrow k lt 0 $$
Видео:Как построить график функции без таблицыСкачать

Ответ: 1) $k gt 0$; 2) k = 0; 3) $k lt 0$
Пример 3. Две параболы с общей вершиной
Найдите соотношение параметров двух парабол, при котором они будут пересекаться в одной точке – вершине парабол.
Пусть уравнения парабол:
$$ y = a_1 x^2+b_1 x+c_1, y = a_2 x^2+b_2 x+c_2 $$
Получаем две пропорции, которым параметры уравнений должны удовлетворять одновременно.
Пример 4. Используя результаты примера 3, найдите две параболы, у которых такая же вершина, как у $y = frac-3x+1$.
$$ x_0 = — frac = — frac<2 cdot frac> = 3, D = b^2-4ac = 3^2-4 cdot frac cdot 1 = 7 $$
Уравнение искомой параболы: $y = ax^2+bx+c$
Пропорции для параметров (см. пример 3):
Пусть для искомых двух парабол a=1 и a=-0,2 (можно взять любые другие значения). Получаем:
$$ <left< begin a = 1 \ b = -6a = -6 \ D = 14a = 14 end right.> Rightarrow <left< begin a = 1 \ b = -6 \ b^2-4ac = 14 end right.> Rightarrow <left< begin a = 1 \ b = -6 \ 36-4c = 14 end right.> Rightarrow <left< begin a = 1 \ b = -6 \ c = frac = 5,5 end right.>$$
$$ <left< begin a = -0,2 \ b = -6a = 1,2 \ D = 14a = -2,8 end right.> Rightarrow <left< begin a = -0,2 \ b = 1,2 \ 1,2^2-4 cdot (-0,2)c = -2,8 end right.> Rightarrow <left< begin a = -0,2 \ b = 1,2 \ c = — frac = -5,3 end right.> $$
$$ y = frac-3x+1, y = x^2-6x+5,5, y = -0,2x^2+1,2x-5,3 $$
имеют общую вершину (3;-3,5)
Пример 5. Комета движется по параболической траектории, которая в выбранной системе координат описывается уравнением $y = frac-2x+5$.
Космический аппарат запускается из начала координат и также движется по параболической траектории. Рассчитайте уравнение этой траектории так, чтобы её вершина совпала с вершиной траектории кометы.
Координаты вершины траектории кометы:
$$ x_0 = -frac = -frac<2 cdot frac> = 3, D = b^2-4ac = 2^2-4 cdot frac cdot 5 = — frac $$
Уравнение траектории космического аппарата: $y = ax^2+bx+c$.
Аппарат запускается из начала координат, т.е. его траектория пересекается с осью OY в точке (0;0). Значит, в уравнении параболы c = 0.
Пропорции для параметров (см. пример 3) с учетом c = 0:
Уравнение траектории космического аппарата с «перехватом» кометы в вершине:
💥 Видео
Квадратичная функция и ее график. 8 класс.Скачать

Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Нахождение координат точек пересечения графика функции с осями координатСкачать

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Не выполняя построения графиков, найдите координаты точки пересечения прямых. Алгебра 7 класс.Скачать

Решение квадратных неравенств графическим методом. 8 класс.Скачать

98 Алгебра 9 класс Найдите координаты точек пересечения графиков функцииСкачать

Точка пересечения графиков линейной и квадратичной функций (продолжение). 23 задание ОГЭСкачать
Занятие 1. График линейной функции y=kx+bСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Графики функций. Задание №11 | Математика ОГЭ 2023 | УмскулСкачать

Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

Квадратичная функция за 5 минутСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать