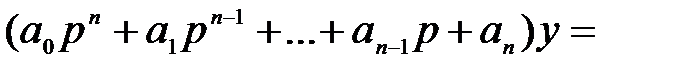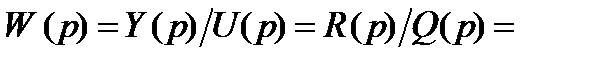Стационарные линейные непрерывные САУ наиболее часто описываются линейными дифференциальными уравнениями с постоянными коэффициентами:

В этом уравнении 




Применяется также операторная форма записи уравнения (2.9):

В этом уравнении через « 

Заметим, что по сложившейся традиции символ « 

За многолетнюю историю развития ТАУ сложились традиции формальной записи линейных дифференциальных уравнений, описывающих стационарные САУ. В учебной литературе по ТАУ они рассматриваются как стандартные формы записи дифференциальных уравнений. Рассмотрим эти формы записи на примере линейной системы второго порядка:


или в операторной форме

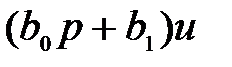
Первая стандартная символическая форма записи уравнения (2.11) имеет следующий вид:

где 



Форма (2.13) представляет собой операторно-структурное описание системы, т.е. в виде операторов звеньев, составляющих структурную схему системы (далее эти понятия разъясняются), и связей между ними. В этой форме 

Из изложенного выше следует, что уравнение (2.9) в этой форме перепишется в следующем виде:

где 


Во второй стандартной форме записи дифференциального уравнения используется передаточная функция системы, которая для рассматриваемого примера (2.11) имеет вид
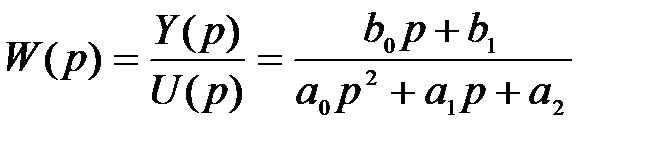
Передаточная функция САУ, поведение которой во времени описывается уравнением (2.9), имеет следующий вид :
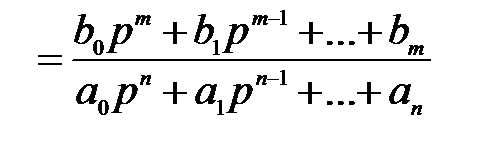
В формуле (2.15) через 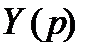




Вторая стандартная форма записи дифференциального уравнения имеет следующий вид:

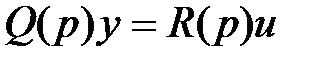
В (2.16) 


Из сравнения первой и второй стандартных форм записи дифференциальных уравнений следует, что с математической точки зрения различие между этими формами весьма несущественно и состоит лишь в различном представлении коэффициентов уравнений. В ТАУ принято называть уравнения вида (2.9) — (2.14), (2.16) уравнениями типа «вход-выход».
Третья стандартная форма записи дифференциального уравнения принципиально отличается от форм записи, описанных выше. В этой форме записи используются переменные состояния. Отметим, что понятие «состояние» является базовым в современной ТАУ (СТАУ). Переменные состояния — это промежуточные переменные системы (рис.2.2), число которых равно ее порядку 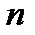
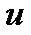



Рис.2.2 — Состояние системы | Переменные состояния называют также координатами состояния, так как их совокупность задает вектор состояния  . . |
Множество возможных положений этого вектора образует векторное пространство 
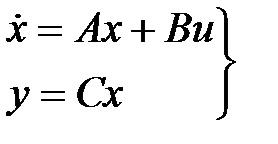
где 





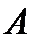
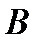

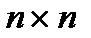


Процессы в САУ в свободном движении (без внешних воздействий) согласно уравнению (2.17) описываются векторно-матричным уравнением 


с характеристическим уравнением

Эти уравнения при определенных начальных условиях дают возможность изучить процессы в системе путем их решения численными методами с использованием ЭВМ.
Разработаны различные способы перехода от уравнений типа «вход-выход» к уравнениям состояния вида (2.17) и наоборот. Один из наиболее распространенных способов состоит в следующем. Пусть САУ описывается уравнением (2.9). Введем обозначения




С помощью этих обозначений преобразуем уравнение (3.1) к следующему виду:
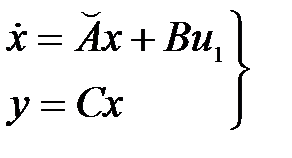
где 



В нашем примере 



Система уравнений (2.19) представляет собой описание линейной непрерывной системы в пространстве состояний 

Если 


Форма уравнений (2.19) с подобными матрицами 

Задание 1
1.1. По дифференциальному уравнению системы:
Для каждого типового звена 1 – 12 (таблицы 2.1) в соответствии с его параметрами вывести дифференциальное уравнение, операторное уравнение, и выражение передаточной функции.
1.2Математическое описание типового звена системы автоматического регулирования записать в трех формах записи дифференциальных уравнений.
Первая стандартная символическая форма операторно-структурное описание системы, т.е. в виде операторов звеньев.
Во второй стандартной форме записи дифференциального уравнения используется передаточная функция системы.
Третья стандартная форма записи дифференциального уравнения — переменные состояния.
Таблица 2.1 – Исходные коэффициенты
| № п.п. | Наименование звена | а 0 | а 1 | а 2 | b0 | b1 | Примечания |
| Безынерционное (пропорциональное) | к | ||||||
| Инерционное 1-го порядка (апериодическое) | Т | k | |||||
| Инерционное 2-го по- рядка (апериодическое) | Т2 2 | Т1 | k | Т1³2Т2 | |||
| Инерционное 2-го по- рядка (колебательное) | Т2 2 | Т1 | k | Т1 T |
Задание 2
2.1Для каждого звена (таблицы 2.2) по его передаточной функции записать дифференциальное уравнение.
2.2 Математическое описание типового звена системы автоматического регулирования записать в трех формах записи дифференциальных уравнений.
| Вар | Передаточная функция | Значения параметров передаточной функции |
 | а0=1; а1=5; а2 =1,2; а3 =0,9; а4=0,5;в0=1;в1=3; в2=0,8;в3=0,3 | |
 | а0=1; а1=5; а2 =1,2; а3 =0,9; в0=1;в1=3; в2=0,8 | |
 | а0=1; а1=5; а2 =1,2; в0=1; в1=3; | |
 | а0=1; а1=5; а2 =1,2; а3 =0,9; а4=0,5; в0=10 | |
 | а0=1; а1=5; а2 =1,2; а3 =0,9; в0=10 | |
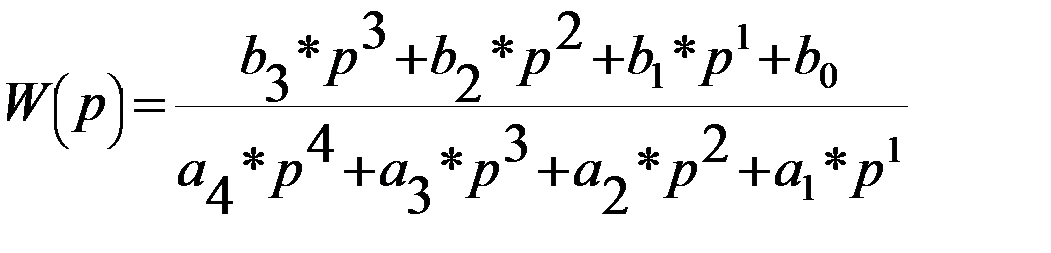 | а0=1; а1=5; а2 =1,2; а3=0,9;а4=0,5;в0=1;в1=3; в2=0,8;в3=0,3 | |
 | Т0=2; Т1=4; Т2=1,1;Т3=0,9 | |
 | Т0=2; Т1=4; Т2=1,1;Т3=1,1;Т4=,9 | |
 | К= 10;Т1=4; Т2=1,1;Т3=0,9 | |
 | К= 10; Т2=1,1;Т3=0,9 Т4=0,9 | |
 | Т0=0,7; Т1=3;Т2=1,2;Т3=0,9;Т4=0,8;Т5=0,5 | |
 | К=10 Т0=0,7; Т1=3;Т2=1,2;Т3=0,9;Т4=0,8;Т5=0,5; |
Задание №3
3.1 Для заданной схемы необходимо составить операторное уравнение для каждого элемента схемы САУ.
3.2. Определить входные и выходные величины каждого элемента, и определить передаточные функции отдельных элементов функциональной схемы.
Формы записи дифференциальных уравнений.
3.3Сформировать математическое описание систем автоматического регулирования в виде структурной схемы в буквенном и числовом обозначениях.
3.4 Сформировать математическое описание систем автоматического регулирования в виде третьей стандартной формы записи дифференциального уравнения — В переменных состояния САУ описываемых векторно-матричным уравнением.
Схема, показанная на рисунке 2.2, представляет собой САР температуры в помещении. Объектом регулирования (ОР) в данной системе является помещение, для которого регулируемая величина — температура внутри помещения Ө, регулирующее (управляющее) воздействие — температура воздуха ӨК, поступающего из калорифера, возмущающее воздействие — изменения внешних факторов f(в общем случае изменение температуры атмосферного воздуха, его влажности, скорости ветра). При исследовании системы в качестве основного возмущения следует рассматривать изменение температуры окружающего воздуха.
Воспринимающим органом — ВО (датчиком, чувствительным элементом) в данной САР является терморезистор RД, включенный в мостовую схему, обеспечивающую с помощью резистора RОзадание необходимого значения температуры в помещении и выполняющую также функции сравнивающего органа — СО (элемента сравнения). Усиление сигнала разбалансаΔU(сигнала рассогласования) измерительной мостовой схемы обеспечивается посредством усилителя. Усиленный сигнал Uобеспечивает вращение двухфазного исполнительного двигателя, который изменяет перемещение клапана (заслонки) на трубопроводе подачи парав калорифер, чем достигается изменение температуры воздуха на входе калорифера — регулирующего воздействия на объектерегулирования.
 |
1 — помещение; 2 — теплообменник (калорифер), 3 — измерительная мостовая схема; 4 — двухфазный исполнительный двигатель, 5 — дифференциальный магнитный усилитель; 6 — клапан (заслонка)
Рис. 2.2. Схема САР температуры
Динамические свойства объекта регулирования и элементов системы описываются следующими уравнениями:
где То, Т2, Т3, Т4 — постоянные времени, с; Ө — значение температуры воздуха в помещении, °С, Ө к — значение температуры воздуха на выходе калорифера, °С; к, к1, к2, к3, к4— коэффициенты передачи; f— возмущающее воздействие на объекте регулирования; Uд —падение напряжения на термодатчике, В; ΔU— напряжение на выходе мостовой схемы (сигнал рассогласования), В; μ. — линейное перемещение клапана, см; U0 — задающий сигнал, В.
Значения параметров элементов САР по вариантам даны в таблице 2.3.
Заданное значение температуры в помещении Ө = 20 °С.
Значения параметров элементов САР
| Вариант | Т0, с | Т2, с | к | к1, В/ 0 С | к4 | к2, см/(В*с) | f,. 0 С | К3, °С/см |
| 0,06 | 0,2 | 0,2 | 0,002 | -11 | ||||
| 0,07 | 0,25 | 0,3 | 0,001 | |||||
| 0,08 | 0,3 | 0,25 | 0,0018 | -8 | ||||
| 0,09 | 0,35 | 0,2 | 0,002 | |||||
| 0,10 | 0,4 | 0,2 | 0,002 | -5 | ||||
| 0,50 | 0,18 | 0,25 | 0,003 | |||||
| 0,055 | 0,19 | 0,4 | 0,0035 | |||||
| 0,06 | 0,17 | 0,4 | 0,0025 | -15 | ||||
| 0,06 | 0,25 | 0,2 | 0,0016 | |||||
| 0,08 | 0,4 | 0,15 | 0,0014 | -18 |
Примечание. Для всех вариантов постоянные времени Т3 = 20 с, Т4=0,5 с.
Схема САР, приведенная на рисунке 2.3, обеспечивает стабилизацию угловой скорости электродвигателя постоянного тока который совместно с рабочим механизмом является объектом регулирования. Регулируемая величина объекта — угловая скорость двигателя ω, регулирующее воздействие — напряжение Uг,подаваемое от генератора на якорь двигателя. Возмущающее воздействие на объекте регулирования — момент сопротивления Мс, создаваемый рабочим механизмом. Угловая скорость двигателя ωконтролируется тахогенератором, сигнал которого Uтг, пропорциональный скорости, сравнивается с задающим сигналом U3. Сигнал рассогласования ΔU = U3— UTг усиливается магнитным усилителем и воздействует на обмотку возбуждения генератора, выполняющего функции исполнительного органа (элемента).
Динамические свойства объекта регулирования и элементов САР описываются следующими уравнениями:
гдеТд, Ту, Tv — постоянные времени, с; Кд, Км, Ктг, Ку, Кг — коэффициенты передачи соответствующих элементов систем
1 — задающий потенциометр; 2 — магнитный усилитель; 3 — генератор; 4 — двигатель; 5 — тахогенератор; 6 — рабочий механизм
Рис. 2.3. Схема САР угловой скорости электродвигателя
Значения параметров элементов САР
| Вариант | Ту, с | Ку | Кг | Тг, с | Кд, рад/ с*В | Тд, с | Км рад/ с*Н* м | Мс, Н*м | Кгг, В*с/ рад |
| 0,020 | 4,0 | 2,0 | 0,10 | 1,0 | 0,5 | 0,02 | 1,0 | ||
| 0,015 | 5,0 | 1,8 | 0,12 | 0,95 | 0,60 | 0,03 | 0,9 | ||
| 0,018 | 4,5 | 1,7 | 0,15 | 0,85 | 0,70 | 0,04 | |||
| 0,022 | 6,0 | 1,5 | 0,20 | 0,8 | 0,80 | 0,05 | 0,7 | ||
| 0,020 | 5,8 | 1,6 | 0,16 | 1,5 | 0,65 | 0,06 | 0,6 | ||
| 0,025 | 4,2 | 2,0 | 0,25 | 1,4 | 0,75 | 0,07 | 0,5 | ||
| 0,020 | 3,5 | 2,7 | 0,22 | 1,3 | 0,80 | 0,08 | 0,4 | ||
| 0,028 | 6,2 | 2,1 | 0,30 | 1,2 | 0,75 | 0,02 | 0,5 | ||
| 0,018 | 6,5 | 2,3 | 0,16 | 1,0 | 0,50 | 0,013 | 0,6 | ||
| 0,014 | 7,0 | 2,5 | 0,20 | 1,25 | 0,80 | 0,015 | 0,7 |
Значения параметров объекта регулирования и элементов системы для различных вариантов указаны в таблице 2.4. Заданное значение угловой скорости ω = 40 рад/с.
На рисунке 2.4 изображена схема САР давления Р в ресивере (воздухосборнике) 1, который является в данной системе объектом регулирования. Давление в ресивере регулируется посредством изменения количества воздуха Q, зависящего от положения заслонки 2, т.е. от ее линейного перемещения Х3, которое можно рассматривать как регулирующее воздействие на входе объекта регулирования. Внешним возмущением, вызывающим отклонение регулируемой величины — давления Р, является изменение расхода сжатого воздуха Qc.
Рис 2.4 Схема САР давления Р в ресивере
Давление в данной системе контролируется с помощью сильфонного датчика 3, выходная величина которого — перемещение Хс сильфона 5 однозначно зависит от разности сил ΔF= F0— Fp, где Fp— сила, создаваемая давлением Р, F0— сила натяжения пружины 6, которое можно изменять винтом 7.
Перемещение сильфона Хсс помощью потенциометрического преобразователя 4 преобразуется в электрический сигнал — напряжение U, которое усиливается электронным усилителем 8. Выходной сигнал усилителя Uyуправляет электромагнитным приводом 9, связанным с заслонкой 2,
В данной САР сильфонный датчик выполняет функции воспринимающего, задающего и сравнивающего органов. Как воспринимающий орган он контролирует давление Р, преобразуя его в силу Fp. Задание требуемого давления в ресивере обеспечивается посредством силы F0. Как сравнивающий орган сильфон обеспечивает сравнение величин F0 и Fp, в результате чего, как отмечалось ранее, получается ΔF= F0 — Fp — сигнал рассогласования.
Динамические свойства объекта регулирования и элементов САР описываются следующей системой уравнений:
| заслонкой |
Физическая сущность переменных, входящих в уравнения, отражена выше в описании схемы САР. Параметры T0, T1, T2, T3 и К0, Кq, Кв, Кc, Кп, Ку, К3 — соответственно постоянные времени и коэффициенты передачи. Их размерности и значения по вариантам даны в таблице 2.5. Требуемое значение давления Р = 500 кПа.
Значения параметров элементов САР
| Вариант | Т0,с | Ко КПа/мм | Т1,с | Т2,с | Кс мм/Н | Кв Н/кПа | КQ, Кпа*с/м 3 | ΔQC, м3/с | Кп В/мм | Ку | Т3 | К3 Мм/В |
| 1,3 | 0,2 | 0,045 | 2,5 | 0,5 | 0,1 | 0,2 | 0,01 | |||||
| 0, 25 | 0 ,04 | 2,5 | 0,5 | -0, 2 | 0,2 | 0,01 | ||||||
| 0,6 | 3,5 | 0,34 | 0,022 | 2,5 | 0,5 | 0,3 | 0,2 | 0,01 | ||||
| 4,8 | 0,25 | 0,035 | 2,5 | 0,5 | -0,15 | 0,2 | 0,01 | |||||
| 0,7 | 4,5 | 0,3 | 0,04 | 2,5 | 0,5 | 0,12 | 0, 9 | 0,01 | ||||
| 0,8 | 3,5 | 0,18 | 0, 025 | 2 ,5 | 0,5 | -0,2 | 0 ,2 | 0,01 | ||||
| 0,4 | 4,4 | 0,25 | 0,03 | 2,5 | 0,5 | 0,11 | 0,2 | 0,01 | ||||
| 0,65 | 5,5 | 0,2 | 0,02 | 2,5 | 0,5 | -0,12 | 0,2 | 0,01 | ||||
| 0, 7 | 0, 4 | 0 ,025 | 2,5 | 0,5 | 0,14 | 0,2 | 0,01 | |||||
| 0,55 | 0,25 | 0,035 | 2,5 | 0,5 | -0,14 | 0,2 | 0,01 |
На электрических станциях при производстве электроэнергии предъявляют определенные требования к стабильности частоты f генерируемой ЭДС. Частота f однозначно определяется угловой скоростью ω рабочего колеса гидротурбины. В связи с этим гидротурбины на электростанциях оснащают САР угловой скорости. На рисунке 2.5 показана схема одного из вариантов такой САР.
В данной системе объектом регулирования является гидротурбина 1, регулируемой величиной — угловая скорость ω .Она при постоянном расходе воды изменяется в зависимости от нагрузки на валу турбины, т. е. от мощности Р, которая потребляется от генератора 2 (с увеличением мощности угловая скорость снижается, с уменьшением — возрастает). Таким образом, мощность Р является внешним возмущающим воздействием на объекте регулирования. Для регулирования угловой скорости предусмотрена заслонка 3, с помощью которой изменяется расход воды через турбину. Он однозначно зависит от вертикального перемещения X заслонки. Следовательно, перемещение заслонки X можно рассматривать как регулирующее воздействие объекта регулирования. Угловая скорость ω контролируется посредством тахогенератора 4, ЭДС Е которого сравнивается с задающим напряжением U0. Сигнал рассогласования Δ U через усилитель 5 управляет посредством электродвигателя 6 и редуктора 7 заслонкой 3.
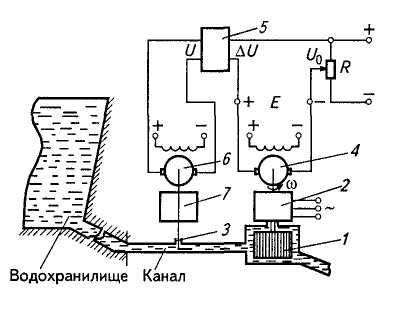 |
Рис. 2.5 Схема САР угловой скорости рабочего колеса гидротурбины
Динамические свойства элементов САР описываются следующей системой уравнений:
Видео:Операционное исчисление. Решить неоднородное дифференциальное уравнение 2 порядкаСкачать

Запишем дифференциальное уравнение в операторной форме
Сущность операторного метода заключается в том, что функции 


Изображение 

 . . | (1) |
В сокращенной записи соответствие между изображением и оригиналом обозначается, как:

Следует отметить, что если оригинал 

В качестве примера в табл. 1 приведены изображения некоторых характерных функций, часто встречающихся при анализе нестационарных режимов.
Таблица 1. Изображения типовых функций
Оригинал  | Изображение  |
| A |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Некоторые свойства изображений
- Изображение суммы функций равно сумме изображений слагаемых:


С использованием этих свойств и данных табл. 1, можно показать, например, что

Изображения производной и интеграла
В курсе математики доказывается, что если 



Таким образом, для напряжения на индуктивном элементе можно записать
или при нулевых начальных условиях

Отсюда операторное сопротивление катушки индуктивности

Аналогично для интеграла: если 

С учетом ненулевых начальных условий для напряжения на конденсаторе можно записать:

или при нулевых начальных условиях

откуда операторное сопротивление конденсатора

Закон Ома в операторной форме
Пусть имеем некоторую ветвь 
сложной цепи. Замыкание ключа во внешней цепи приводит к переходному процессу, при этом начальные условия для тока в ветви и напряжения на конденсаторе в общем случае ненулевые.
Для мгновенных значений переменных можно записать:

Тогда на основании приведенных выше соотношений получим:

 , , | (2) |
где 
Следует обратить внимание, что операторное сопротивление 


Уравнение (2) есть математическая запись закона Ома для участка цепи с источником ЭДС в операторной форме. В соответствии с ним для ветви на рис. 1 можно нарисовать операторную схему замещения, представленную на рис. 2.
Законы Кирхгофа в операторной форме
Первый закон Кирхгофа: алгебраическая сумма изображений токов, сходящихся в узле, равна нулю

Второй закон Кирхгофа:алгебраическая сумма изображений ЭДС, действующих в контуре, равна алгебраической сумме изображений напряжений на пассивных элементах этого контура

При записи уравнений по второму закону Кирхгофа следует помнить о необходимости учета ненулевых начальных условий (если они имеют место). С их учетом последнее соотношение может быть переписано в развернутом виде

В качестве примера запишем выражение для изображений токов в цепи на рис. 3 для двух случаев: 1 — 

В первом случае в соответствии с законом Ома 
Во втором случае, т.е. при 
откуда 


Переход от изображений к оригиналам
Переход от изображения искомой величины к оригиналу может быть осуществлен следующими способами:
1. Посредством обратного преобразования Лапласа

которое представляет собой решение интегрального уравнения (1) и сокращенно записывается, как:

На практике этот способ применяется редко.
2. По таблицам соответствия между оригиналами и изображениями
В специальной литературе имеется достаточно большое число формул соответствия, охватывающих практически все задачи электротехники. Согласно данному способу необходимо получить изображение искомой величины в виде, соответствующем табличному, после чего выписать из таблицы выражение оригинала.
Например, для изображения тока в цепи на рис. 5 можно записать

Тогда в соответствии с данными табл. 1

что соответствует известному результату.
3. С использованием формулы разложения
Пусть изображение 

где 
Это выражение может быть представлено в виде суммы простых дробей
 , , | (3) |
где 

Для определения коэффициентов 


При

Рассматривая полученную неопределенность типа 


Поскольку отношение 

 . . | (4) |
Соотношение (4) представляет собой формулу разложения. Если один из корней уравнения 


В заключение раздела отметим, что для нахождения начального 

которые также могут служить для оценки правильности полученного изображения.
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
- В чем заключается сущность расчета переходных процессов операторным методом?
- Что такое операторная схема замещения?
- Как при расчете операторным методом учитываются ненулевые независимые начальные условия?
- Какими способами на практике осуществляется переход от изображения к оригиналу?
- Для чего используются предельные соотношения?
- Как связаны изображение и оригинал в формуле разложения? Какие имеются варианты ее написания?
С использованием теоремы об активном двухполюснике записать операторное изображение для тока через катушку индуктивности в цепи на рис. 6.
Ответ: 
С использованием предельных соотношений и решения предыдущей задачи найти начальное и конечное значения тока в ветви с индуктивным элементом.
Ответ: 
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Формы записи линейных неоднородных дифференциальных уравнений
4.4. Формы записи линейных неоднородных дифференциальных уравнений
При описании динамики САУ и ее элементов в виде линейных неоднородных дифференциальных уравнений используют либо операторную форму Коши, либо форму в преобразованиях Лапласа, как это было представлено в предыдущем разделе.
Рассмотрим операторную форму записи на примере. Пусть неоднородное линейное дифференциальное уравнение, описывающее динамику САУ, имеет вид

Операцию дифференцирования обозначим оператором p,

Используя эти обозначения, (4.27) перепишется как




В итоге получим компактную форму записи в операторном виде

Теперь получим форму записи неоднородного линейного дифференциального уравнения n-го порядка в преобразованиях Лапласа. Это уравнение в стандартном виде представлено как

Используя свойства преобразования Лапласа, получим


можем записать сразу решение дифференциального уравнения (4.30) в преобразованиях Лапласа


где изображение решения дифференциального уравнения или выходной величины y(t) равно произведению дробно-рациональной функции W(s) и изображения по Лапласу входной величины x(t).
уравнение 
решение уравнения в изображениях

при 
Тогда решение исходного уравнение в преобразованиях Лапласа

или, используя таблицы обратного преобразования Лапласа, получим
4.5. Виды передаточных функций САУ
Отношение оператора воздействия к собственному оператору называется передаточной функцией в операторной форме.
Передаточная функция относительно входной величины x(t)

Передаточная функция относительно возмущающего воздействия f(t)

Используя передаточные функции (4.32) и (4.33), уравнение (4.27) можно переписать

Уравнения (4.32)-(4.33) называют уравнениями в символической или операторной форме записи.
Отношение (4.31) изображения выходной величины к изображению входной величины при нулевых начальных условиях называют передаточной функцией в форме изображений Лапласа.
Если звено или система имеют несколько входов, то при определении передаточной функции относительно какой-либо одной входной величины остальные полагают равными нулю.
Найдем передаточные функции в форме изображений Лапласа для звена, описанного уравнением (4.27)
Используя свойства линейности и дифференцирования функций-оригиналов в преобразовании Лапласа при нулевых начальных условиях, получим

где 




W1(s) называют передаточной функцией по управляющему воздействию,
W2(s) – передаточной функцией по возмущающему воздействию.
Сравнивая передаточные функции (4.32) и (4.33) с (4.36), заметим, что они полностью совпадают при замене аргументов p на s. Это совпадение возможно только для стационарных систем. Если 


Используя передаточные функции (4.36) и уравнение (4.35),можно записать решение исходного уравнения в преобразованиях Лапласа

Это решение адекватно решению исходного дифференциального уравнения (4.27) только при нулевых начальных условиях.
Следует отметить, что линейные дифференциальные уравнения с постоянными коэффициентами не выше второго порядка, описывающие
поведение звеньев и САУ, записываются в стандартной форме. В этом случае все члены, содержащие выходную переменную и ее производные, записывают в левой части уравнения, все остальные члены — в правой, а коэффициент при выходной переменной делают равным единице.
Уравнение (4.27) в стандартной форме принимает вид:

где 


Стандартную форму остальных звеньев рассмотрим ниже.
4.6. Характеристики САУ и их элементов
Для описания линейных стационарных систем и их элементов используют различные виды характеристик. Они являются или непосредственными вынужденными движениями систем и их элементов в зависимости от времени, или определяют соотношения параметров этих движений при подаче на вход типовых воздействий. К основным характеристикам относятся частотные и временные.
4.6.1. Частотные характеристики
Частотные характеристики с физической точки зрения являются
функциями параметров реакции САУ и ее элементов на гармонические воздействия. Для определения частотных характеристик рассмотрим решение уравнения (4.30) при
Решение уравнения (4.30) имеет вид

где ya(t) — общее решение однородного уравнения;

Составляющая уa(t) определяет свободные движения системы или переходной процесс, который со временем затухает, если система устойчива. Составляющая yb(t) определяет вынужденное движение системы под воздействием x(t) . Найдем yb(t) при заданном гармоническом воздействии x(t). Согласно формуле Эйлера, представим

где 

Найдем отдельно каждое из этих решений.
Для этого определим производные от x1(t) с учетом того, что 
Уравнение (4.30) после его преобразования по Лапласу и подстановки в правую часть выражений (4.40) примет вид

На основе свойств неоднородного линейного дифференциального уравнения, частное решение будем искать в виде

где оператор 



Функцию 



Функцию 




Тогда частное решение неоднородного уравнения (4.30) при x1(t)

Аналогично получаем решение 
Таким образом, для устойчивых систем и их элементов, находящихся под воздействием гармонического сигнала, после окончания переходного процесса выходная величина также изменяется по гармоническому закону с той же частотой, но с другой амплитудой и фазой. При чем А(w) является отношением амплитуд выходной и входной синусоид в зависимости от частоты гармоники. 
Частотную характеристику 
При заданной 




U(
V(
A(



Графики этих функций называют соответствующими частотными характеристиками исследуемой системы автоматического управления.
Кроме перечисленных частотных характеристик, используют еще и логарифмические частотные характеристики. Логарифмическая амплитудно-частотная функция определяется как 


При построении ЛАЧХ по оси абсцисс откладывают частоту в логарифмическом масштабе. Для построения ЛАЧХ по оси ординат откладывают в дБ величину 20lg A(

Шкалу частот по оси абсцисс разбивают в масштабе lg(
Особенность lg масштаба состоит в том, что отрезок, изображающий октаву или декаду, имеет одну и ту же длину, не зависящую от частоты и равную соответственно lg 2 или I (pис.4.4):
Рис.4.4 • Логарифмический масштаб
где по оси абсцисс пишут не значение 1g(




частоты 


Единица измерения L(

Ось ординат при построении ЛАЧХ строится через произвольную точку 

Зависимость (4.42) можно представить как


Откуда возможно получить аналитические зависимости для определения частотных характеристик на основе (4.43) и (4.49):




5.2. Временные характеристики
Другой важной характеристикой автоматических систем или звеньев являются переходные и импульсные переходные функции, а так же их графики, которые называются временными характеристиками. Их используют при описании как стационарных, так и нестационарных линейных систем.
Переходной функцией системы (звена) называют функцию, описывающую изменение выходной величины системы (звена) при подаче на ее вход единичного ступенчатого воздействия при нулевых начальных условиях. Переходную функцию обычно обозначают h(t). Иначе, переходная функция h(t) есть функция, описывающая реакцию системы (звена) на единичное ступенчатое воздействие при нулевых начальных условиях.
Аналитически единичное ступенчатое воздействие можно описать так называемой единичной функцией 
График переходной функции — кривая зависимости функции h(t) от времени t — называют переходной характеристикой.
Импульсной переходной или весовой функцией (функцией веса) системы (звена) называют функцию, описывающую реакцию системы (звена) на единичное импульсное воздействие при нулевых начальных условиях; обозначают эту функцию через 
Переходную и импульсную переходную характеристику называют временными характеристиками.
При определении весовой функции было использовано понятие единичного импульса. Физически единичный импульс можно представить как очень узкий импульс, площадь которого равна единице. Математически он описывается функцией 


Перейдем к определению дельта-функции и ее производных. При этом воспользуемся тем обстоятельством, что при решении каких-либо практических задач, как правило, дельта-функция и ее производные встречаются только на промежуточных этапах различных соотношений. В окончательном результате они или вовсе отсутствуют, или фигурируют под знаком интеграла в произведении с какой-либо «обычной» функцией. По этому нет прямой необходимости отвечать на вопрос, что такое дельта-функция сама по себе, а достаточно ответить на вопрос, что означает интеграл от произведения дельта-функции или какой-либо ее производной и обычной функции. Руководствуясь приведенными соображениями, дельта-функцию можно определить так:
дельта-функция есть функция, которая обладает следующими свойствами —


Производные от дельта-функции можно определить по следующим соотношением:


где 


Найдем изображение Лапласа от дельта-функции и ее производных. При этом преобразование Лaпласа будем трактовать как предельное соотношение

Используя соотношения (4.50)-(4,53), нетрудно получить



Рассмотрим линейное неоднородное дифференциальное уравнение n- го порядка с постоянными коэффициентами в общем виде

В изображении Лапласа уравнение принимает вид

где передаточная функция 
Легко проверить, используя формулу (4.55) ,что уравнение (4.57) справедливо и в тех случаях, когда или 
В соответствии с определением весовой функции при 



Таким образом передаточная функция равна изображению Лапласа от весовой функции и соответственно

Последнюю формулу можно использовать для вычисления весовой функции.
Установим связь между весовой и переходной функциями.
Так как 


Сравнив эту формулу с (4.59), нетрудно заметить, что 

Весовая и переходная функции, как и передаточная функция, являются исчерпывающими характеристиками системы (звена) , так как зная их аналитические выражения можно однозначно решить задачу анализа для любой САУ, а именно определить выходной сигнал при произвольном входном воздействии. Действительно, исходя из уравнения (4.57), с помощью теоремы о свертке можно записать

Эта формула, как и уравнение (4.57), справедлива только при нулевых начальных условиях.
4.7. Элементарные звенья САУ и их характеристики
Звеном САУ называют математическую модель элемента или соединения элементов любой части системы. Звенья, как и системы, могут описываться дифференциальными уравнениями высокого порядка и в общем случае их передаточные функции могут быть представлены как

Но их можно представить как соединения типовых или элементарных звеньев, порядок дифференциальных уравнений которых не выше второго.
Из курса алгебры на основании теоремы Безу известно, что полином произвольного порядка можно разложить на простые множители вида


Поэтому передаточную функцию (4.63) можно представить, как произведение простых множителей вида (4.64) и простых дробей вида



Звенья, передаточные функции которых имеют вид простых множителей (4.63) или простых дробей (4.64), называют типовыми или элементарными звеньями.
Прежде чем переходить к изучению элементарных звеньев, вспомним формулы для модуля и аргумента комплексного числа. Пусть комплексное число представлено в виде отношения двух произведений комплексных чисел
Так как 



Таким образом, справедливо следующее правило модулей и аргументов комплексных чисел: модуль комплексного числа, представленного в виде отношения двух произведений комплексных чисел, равен отношению произведения модулей сомножителей числителя к произведению модулей сомножителей знаменателя, а его аргумент — разности суммы аргументов сомножителей числителя и суммы аргументов сомножителей знаменателя.
Пропорциональное звено. Пропорциональным называют звено, которое описывается уравнением 

Частотные и временные функции этого типового эвена имеют вид:







Ha рис. 4.5 представлены некоторые из характеристик пропорционального звена: амплитудно-фазовая частотная характеристика (4.5 а) — это точка К на действительной оси; фазовая частотная
 |
 |




характеристика (или АФЧХ) совпадает с положительной осью частот; логарифмическая амплитудная частотная характеристика (рис. 4.56) параллельна оси частот и проходит на уровне

Интегрирующее звено. Интегрирующим называют звено, которое описывается уравнением 


Остальные частотные и временные функции имеют вид:







АФЧХ (рис.4.6а) интегрирующего звена совпадает с отрицательной мнимой полуосью. ЛФЧХ (рис.4.66) параллельна оси частот и проходит на уровне 

ЛАЧХ (рис.4.6б) — наклонная прямая, проходящая через точку с координатами 



Переходная характеристика представляет собой прямую, проходящую через начало координат с угловым коэффициентом наклона, равным k. (рис.4.6в).

jV U L(w) 
Рис 4.6 Характеристики интегрирующего звена
Дифференцирующее звено. Дифференцирующим называют звено, которое описывается уравнением 

Частотные и временные функции этого звена имеют вид









Рис.4.7 Характеристики дифференцирующего звена
АФЧХ (рис 4.7а) совпадает с положительной мнимой полуосью. ЛФЧХ (рис 4.7б) параллельна оси частот и проходит на уровне 

ЛАЧХ есть прямая линия, проходящая через точку с координатами 

децибел на декаду): 
Апериодическое звено. Апериодическим эвеном первого порядка называют звено, которое описывается уравнением

или передаточной функцией

Это звено также называют инерционным звеном первого порядка. Апериодическое звено в отличие от вышерассмотренных звеньев характеризуется двумя параметрами: постоянной времени T и передаточным коэффициентом k.
Частотная передаточная функция

Умножив числитель и знаменатель на комплексно-сопряженное знаменателю выражение, получим


Амплитудную и фазовую частотные функции можно определить, используя правило модулей и аргументов.
Так как модуль числителя частотной передаточной функции (4.68) равен k, а модуль знаменателя 

Аргумент числителя 


Решив дифференциальное уравнение (4.66) при 



АФЧХ апериодического эвена (рис. 4.8а) есть полуокружность, в чем не трудно убедиться, исключив из параметрических уравнений (4.69) АФЧХ частоту 
ЛАЧХ представлена на рис 4.8б. На практике обычно ограничиваются построением так называемой асимптотической ЛАЧХ (ломаная линия на том же рис 4.86). В критических случаях, когда небольшая погрешность может повлиять на выводы о состоянии исследуемой системы, рассматривают точную ЛАЧХ. Впрочем, точную ЛАЧХ можно легко построить по асимптотической ЛАЧХ, если воспользоваться следующей зависимостью ( L — разность между асимптотической и точной ЛАЧХ):
T = 0,10 0,25 0,40 0,50 1,0 2,0 2,5 4,0 10,0

Частоту 
Рио.4.8 Характеристики апериодического звена
наиболее сильно отличаются при сопрягающей частоте; отклонение при этой частоте примерно 3 дБ.
Уравнение асимптотической ЛАЧХ имеет вид:

Оно получается из уравнения (4.71), если в нем под корнем при 

Согласно полученному уравнению, асимптотическую ЛАЧХ можно строить следующим образом: на уровне 



По АФЧХ или ЛАЧХ легко определить параметры Т и k апериодического звена (рис.4.86).
ЛФЧХ изображена на рис. 4.86. Эта характеристика асимптотически стремится к нулю при 





Переходная характеристика апериодического звена (рис.4.8в) представляет собой экспоненциальную кривую, по которой можно определить параметры этого звена: передаточный коэффициент k определяется по установившемуся значению 
Форсирующее звено. Форсирующим звеном или форсирующим звеном первого порядка называют звено, которое описывается уравнением

или передаточной функцией

Это звено, как и апериодическое, характеризуется двумя параметрами: постоянной времени T и передаточным коэффициентом k.
Частотная передаточная функция

Остальные частотные и временные функции имеют вид:







АФЧХ есть прямая, параллельная мнимой оси и пересекающая действительную ось в точке U=k.(рис. 4.9а). Как и в случае апериодического звена, на практике ограничиваются построением асимптотической ЛАЧХ. Частоту 



ЛФЧХ форсирующего звена можно получить зеркальным отображением относительно оси частот ЛФЧХ апериодического звена и для ее построения можно воспользоваться тем же шаблоном и номограммой, которые используются для построения последней.
Колебательное, консервативное и апериодическое второго порядка звенья. Звено, которое можно описать уравнением


или в другой форме

где, 

Передаточная функция этого звена


Это звено является колебательным, если 



Колебательное звено 

Умножив числитель и знаменатель на комплексно-сопряженное выражение, получим вещественную и мнимую частотные функции колебательного звена:

Фазовая частотная функция, как это видно из АФЧХ (рис 4.10б), изменяется монотонно от 0 до — 


ЛФЧХ (рис.410б) при 


Амплитудная частотная функция
и логарифмическая амплитудно-частотная функция

Уравнение асимптотической ЛФЧX имеет вид


где 


Рис. 4.10 .Характеристики колебательного звена
Следует иметь в виду, что асимптотическая ЛАЧХ (рис 4.10б) при малых значениях коэффициента демпфирования довольно сильно отличается от точной ЛАЧХ. Точную ЛАЧХ можно построить по асимптотической ЛАЧХ, воспользовавшись кривыми отклонений точных ЛАЧХ от асимптотических (рис.4.10г). Решив дифференциальное уравнение (4.72) колебательного звена при 






По переходной характеристике (рис.4.10в) можно определить параметры колебательного звена следующим образом.
📸 Видео
13. Операционное исчисление. Решить неоднородное ДУ 2 порядкаСкачать

Решение диф.уравнений операторным методомСкачать

Операторный метод решения дифференциальных уравнений | Решение задачСкачать

2020 г. Операторный метод (Лапласа) для анализа цепей. Лекция и практикаСкачать

Решение ДУ.Операционный методСкачать

14. Операционное исчисление. Система ДУСкачать

7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

12 Операционное исчисление. Решить однородное ДУ 2 порядка.Скачать

Видеоурок "Системы дифференциальных уравнений"Скачать

Неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами МЕТОДОМ ЛАПЛАСАСкачать

Система дифференциальных уравнений. Операционный методСкачать

Решить задачу Коши для дифференциального уравнения с помощью формулы ДюамеляСкачать