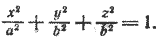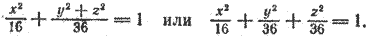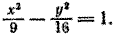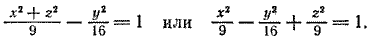Условие
Записать уравнение и определить вид поверхности, полученной при вращении данной линии вокруг указанной оси координат, сделать рисунок.
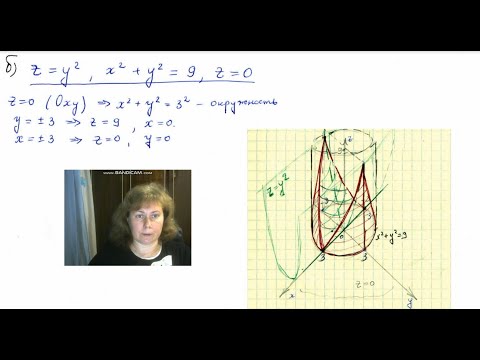
а) y^2-5x^2=5, Oy; б) y=3, z=1, Ox.
Сборник индивидуальных заданий по высшей математике Автор Рябушко ИДЗ 4.2, задание 2.10
Решение
В плоскости xОy:
y^2-5x^2=5 — гипербола (y^2/5)-(x^2/1)=1
В плоскости yОz
y^2-5z^2=5 — гипербола (y^2/5)-(z^2/1)=1
двуполостный гиперболоид: (y^2/5)-(x^2/5)-(z^2/1)=1
см. рис. на скрине 1
2.
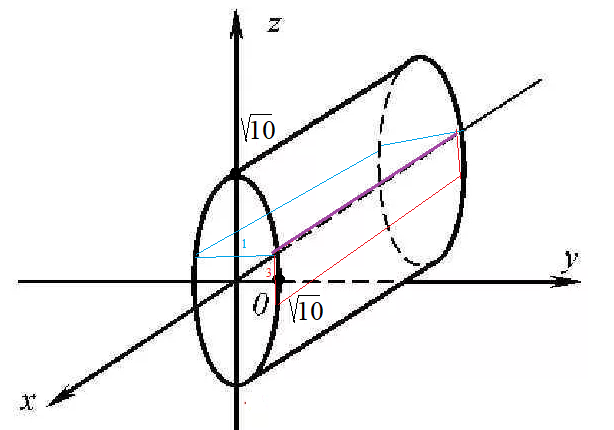
две плоскости y=3; z=1 пересекаются по прямой, параллельной Оси Оx
и проходящей через точку (0;3;1)
Эта прямая при вращении вокруг оси Оx описывает цилиндр.
Точка (3;1) при вращении вокруг (0;0)
описывает окружность радиуса R
[b]y^2+z^2=10[/b]- круговой цилиндр 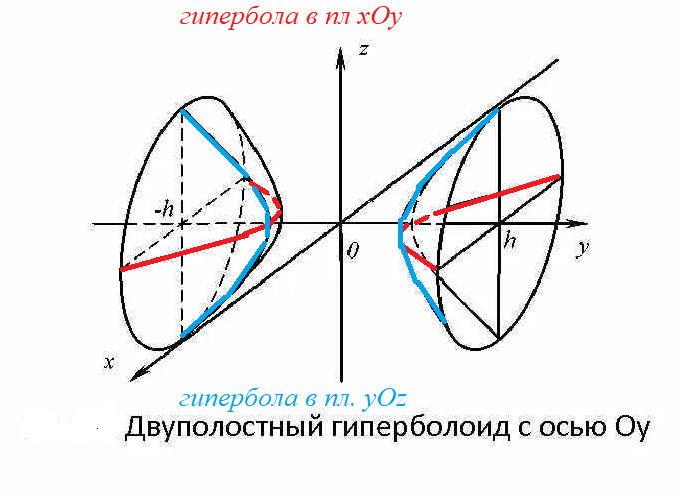
Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Записать уравнение при вращении данной линии вокруг
Глава VI. Простейшие криволинейные поверхности и тела вращения.
§ 75*. Поверхности вращения
1. Пусть в плоскости р задана кривая L и некоторая прямая l. Поверхность, которая получается вращением кривой L вокруг прямой l, называется поверхностью вращения.
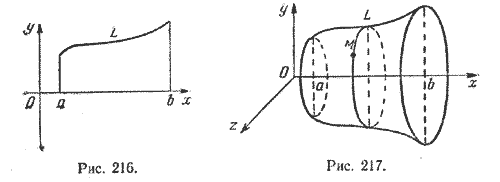
Пусть кривая L лежит в плоскости хОу (рис. 216) и имеет уравнение
y = f(x), х 
Найдем уравнение поверхности, которая получится вращением кривой L вокруг оси Ох (рис. 217).
Очевидно, точка M с координатами (х; у; z), где х 
Действительно, точки (х; у; z) и (х; f(x); 0) лежат на одной окружности с центром в точке (х; 0; 0).
Таким образом, уравнение поверхности, полученной вращением кривой (1) вокруг оси Ох, имеет вид
y 2 + z 2 = (f(x)) 2 , х 
Заметим, что уравнение (2) получается из уравнения (1) следующим образом:
обе части уравнения (1) возводятся в квадрат и y 2 заменяется на y 2 + z 2 ,
В частности, если кривая L задана уравнением
то уравнение поверхности, полученной вращением этой кривой вокруг оси Ох, имеет вид
т. е. просто y 2 заменяем на y 2 + z 2 .
2. Поверхность, которая получается вращением эллипса вокруг одной из его осей, называется эллипсоидом вращения.
Пусть в плоскости хОу эллипс задан уравнением
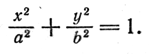
Составим уравнение поверхности, полученной вращением его вокруг оси Ох. Уравнение эллипса (5) приводится к виду (3), следовательно, для получения уравнения эллипсоида вращения достаточно в уравнении (5) y 2 заменить на y 2 + z 2 . После замены получим
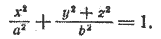
Это уравнение обычно записывают так:
При а > b уравнение (6) определяет эллипсоид вращения, вытянутый вдоль оси Ох (рис. 218), при а 2 на y 2 + z 2 , получим искомое уравнение эллипсоида вращения:
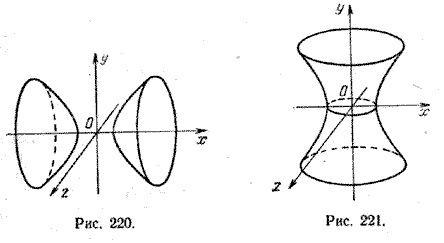
3. Поверхность, которая получается вращением гиперболы вокруг одной из ее осей, называется гиперболоидом вращения. При вращении гиперболы вокруг ее действительной оси получается двуполостный гиперболоид вращения (рис. 220), а при вращении гиперболы вокруг ее мнимой оси получается однополостный гиперболоид вращения (рис. 221).
Пусть в плоскости хОу гипербола задана уравнением
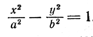
Составим уравнение поверхности, полученной вращением гиперболы вокруг ее действительной оси Ох. Уравнение гиперболы (7) приводится к виду (3); следовательно, для получения уравнения поверхности двуполостного гиперболоида вращения достаточно в уравнении гиперболы (7) y 2 заменить на y 2 + z 2 . После замены получим
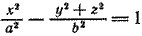
При вращении гиперболы (7) вокруг ее мнимой оси нужно в уравнении (7) x 2 заменить на x 2 + z 2 ; после замены получим
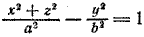
Задача 2. Гипербола с полуосями а = 3 и b = 4 вращается вокруг своей мнимой оси, совпадающей с осью Оу. Центр гиперболы совпадает с началом координат. Составить уравнение поверхности, полученной при вращении этой гиперболы.
Составим уравнение гиперболы:
Чтобы получить уравнение гиперболоида вращения, в уравнении гиперболы x 2 заменим на x 2 + z 2 . После замены получим
4. Поверхность, которая получается вращением параболы вокруг ее оси симметрии, называется параболоидом вращения (рис. 222).
Пусть на плоскости хОу парабола задана уравнением
Для получения уравнения поверхности вращения нужно в уравнении (10) x 2 заменим на x 2 + z 2 ; после замены получим
Отметим одно замечательное свойство этой поверхности. Если внутреннюю поверхность параболоида вращения сделать зеркальной, а в ее фокусе (фокусом параболоида вращения называется фокус вращаемой параболы) поместить источник света, то все лучи света, отражаясь от поверхности параболоида, пойдут параллельно оси параболоида.
Это свойство широко используется при изготовлении светоотражающих устройств (прожекторов, фар автомобиля, кинопроекторов и других приборов).
Задача 3. Составить уравнение поверхности, полученной вращением параболы y 2 = 2х вокруг оси Ох.
Чтобы составить уравнение параболоида вращения, полученного вращением параболы вокруг оси Ох, нужно в уравнении y 2 = 2х заменить y 2 на y 2 + z 2 , после замены получим
5. Если вращать прямую, параллельную какой-либо оси координат, вокруг этой оси, то получится круговая цилиндрическая поверхность.
Пусть дана прямая, лежащая в плоскости yOz и имеющая уравнение у = а. Легко видеть, что поверхность вращения этой прямой вокруг оси Oz имеет уравнение
Эта цилиндрическая поверхность изображена на рис. 223.
Задача 4. Составить уравнение цилиндрической поверхности, полученной вращением прямой у = 3, лежащей в плоскости хОу вокруг оси Ох.
В уравнении y 2 = 3 2 заменим y 2 на y 2 + z 2 , в результате получим
6. Пусть дана прямая, лежащая в плоскости yOz и проходящая через начало координат:
y = kz, k =/= 0.
Очевидно, уравнение поверхности вращения этой прямой вокруг оси Oz имеет вид
Полученное уравнение является уравнением искомой поверхности вращения, которая называется круговой конической поверхностью (рис. 224).
Задача 5. Составить уравнение поверхности вращения прямой 2х = 3у, z =0 вокруг оси Ох.
Из уравнения 3у = 2х, используя формулу (2), находим 9(y 2 + z 2 ) = 4x 2 . Это и есть искомое уравнение.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Записать уравнение при вращении данной линии вокруг
Рассмотрим сечение плоскостью у = 0. Получается парабола = z, её ветви направлены вверх, вершина в точке (0, 0, 0).
Рассмотрим сечение плоскостью x = h. Это опять парабола:
Её ветви направлены вниз, вершина смещена по оси OZ на величину . то есть находится в точке . Заметим, что эта точка лежит на параболе
Теперь, изменяя h, видим, что поверхность гиперболического параболоида состоит из парабол, расположенных в плоскостях x = h, вершины которых находятся на параболе .
💡 Видео
§64 Поверхности вращенияСкачать

Поверхность вращения.Скачать

Поверхности второго порядкаСкачать

Урок 93. Основное уравнение динамики вращательного движенияСкачать

Интегралы №13 Объем тела вращенияСкачать

Вращательное движение. 10 класс.Скачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Вращение вокруг вертикальной прямой. Метод оболочекСкачать

9 класс, 7 урок, Уравнение прямойСкачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Вычисление объемов тел вращения (применение определенного интеграла)Скачать
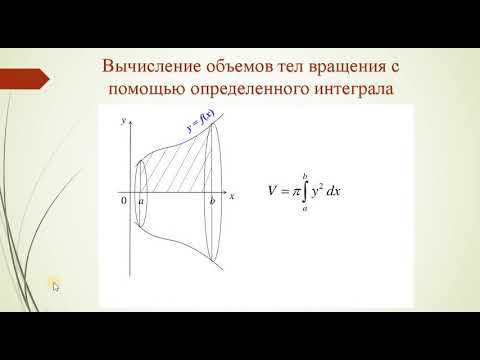
Поверхности второго порядка. Поверхности вращенияСкачать
Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Составляем уравнение прямой по точкамСкачать

Площадь поверхности вращенияСкачать

Построение кривой в полярной системе координатСкачать

Объем тела, образованного вращением кривой вокруг оси хСкачать