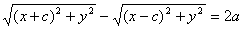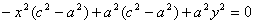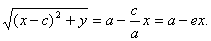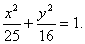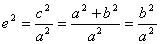Записать уравнение окружности проходящей через указанные точки и имеющей центр в точке а параболы

Видео:№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

Задача 62271 Записать уравнение окружности.

Условие

Записать уравнение окружности, проходящей через
указанные точки и имеющий центр в точке A , сделать
рисунок
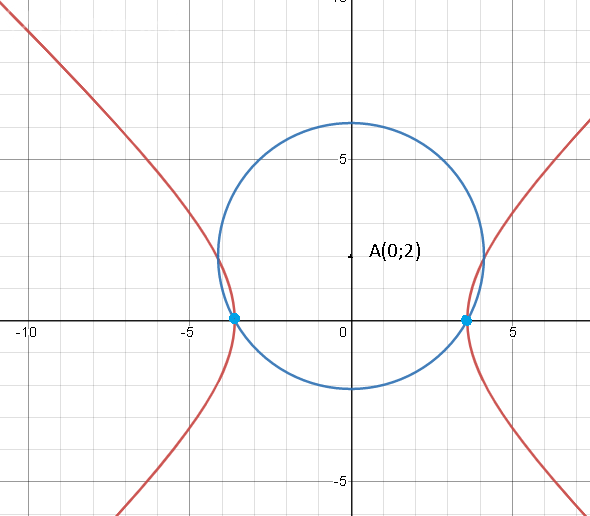
1. Вершины гиперболы
12x^2 -13y^2 = 156, А(0; 2)

Решение

(x^2/13)-(y^2/12)=1- каноническое уравнение гиперболы с действительной осью Ох

Значит вершины гиперболы в точках

(-sqrt(13);0) и (sqrt(13);0)

Каноническое уравнение окружности с центром в
А(0; 2)

Подставляем координаты вершин гиперболы:

(-sqrt(13);0) ((-sqrt(13)^2-0)^2+(0-2)^2=R^2 ⇒ R^2=13+4=17

и (sqrt(13);0)((sqrt(13)^2-0)^2+(0-2)^2=R^2 ⇒ R^2=13+4=17

О т в е т. (x-0)^2+(y-2)^2=17 или [b] x^2+(y-2)^2=17[/b]

Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Записать уравнение окружности, проходящей через указанные точки имеющийся центр в точке

Записать уравнение окружности, проходящей через обозначенные точки имеющийся центр в точке А: вершину гиперболы х^2-16y^2=64, A(0,-2)

• Ljubov Lomizova
• Математика 2019-10-10 02:53:17 0 1

Уравнение окружности имеет вид (х х₀) + (y y₀) = R, где R радиус окружности, х₀ и у₀ координаты центра окружности.

Так как центр окружности имеет координаты А(0; -2), то х₀ = 0, у₀ = -2.

Получается уравнение (х 0) + (y + 2) = R, х + (y + 2) = R.

Приведем уравнение гиперболы к каноническому виду:

Поделим уравнение на 64:

Вычислим координаты вершин гиперболы:

у = 0; (х/8) — (0/2) = 1; х/64 = 1; х = 64; х = -8 и х = 8.

Верхушки параболы имеют координаты (8; 0) и (-8; 0).

Подставим координаты хоть какой из вершин в уравнение нашей окружности, чтоб вычислить квадрат радиуса:

Следовательно, уравнение окружности имеет вид х + (y + 2) = 68.

Видео:Уравнение окружности (1)Скачать

Написать уравнение окружности имеющей центр в фокусе параболы у2 2рх

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Задача 54735 2. Записать уравнение окружности.

Условие

2. Записать уравнение окружности, проходящей через указанные точки и имеющей центр в точке А.
2.3 Фокусы гиперболы 24y2 – 25×2 = 600, A(0, –8)

Решение

[m]24y^2 – 25x^2 = 600 [/m]

Делим обе части уравнения на 600

Гипербола, фокусы которой расположены [b]на оси Оу.[/b]

F_(1)(0;-7) и F_(2)(0;7) — фокусы
Далее, что-то не так в условии:

Три точки F_(1)(0;-7) и F_(2)(0;7) и А (0;-8) лежат на одной прямой.

Не провести окружность с таким условием

(x+8)^2+y^2=113 — уравнение окружности

либо уравнение гиперболы

[m]24x^2 – 25y^2 = 600 [/m]

и фокусы в точках F_(1)(-7;0) и F_(2)(7;8)

Тогда
x^2+(y+8)^2=113 — уравнение окружности

Видео:№970. Напишите уравнение окружности, проходящей через точку А (1; 3), если известноСкачать

Написать уравнение окружности имеющей центр в фокусе параболы у2 2рх

Ах 2 + 2Вху + Су 2 + 2 Dx + 2 Ey + F = 0.

Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.

1) — уравнение эллипса.

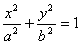
2) — уравнение “мнимого” эллипса.

3) — уравнение гиперболы.

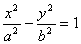
4) a 2 x 2 – c 2 y 2 = 0 – уравнение двух пересекающихся прямых.

5) y 2 = 2 px – уравнение параболы.

6) y 2 – a 2 = 0 – уравнение двух параллельных прямых.

7) y 2 + a 2 = 0 – уравнение двух “мнимых” параллельных прямых.

8) y 2 = 0 – пара совпадающих прямых.

9) ( x – a ) 2 + ( y – b ) 2 = R 2 – уравнение окружности.

В окружности ( x – a ) 2 + ( y – b ) 2 = R 2 центр имеет координаты ( a ; b ).

Пример. Найти координаты центра и радиус окружности, если ее уравнение задано в виде:

2 x 2 + 2 y 2 – 8 x + 5 y – 4 = 0.

Для нахождения координат центра и радиуса окружности данное уравнение необходимо привести к виду, указанному выше в п.9. Для этого выделим полные квадраты:

x 2 + y 2 – 4 x + 2,5 y – 2 = 0

x 2 – 4 x + 4 –4 + y 2 + 2,5 y + 25/16 – 25/16 – 2 = 0

( x – 2) 2 + ( y + 5/4) 2 – 25/16 – 6 = 0

( x – 2) 2 + ( y + 5/4) 2 = 121/16

Отсюда находим О (2; -5/4); R = 11/4.

Определение. Эллипсом называется линия, заданная уравнением .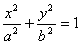

О пределение. Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

у

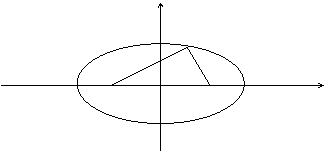
с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением:

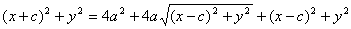
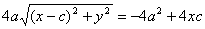
Доказательство: В случае , если точка М находится на пересечении эллипса с вертикальной осью, r ₁ + r ₂ = 2 (по теореме Пифагора). В случае , если точка М находится на пересечении эллипса с горизонтальной осью, r ₁ + r ₂ = a – c + a + c . Т.к. по определению сумма r ₁ + r ₂ – постоянная величина, то , приравнивая, получаем:

a 2 = b 2 + c 2

Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.

Определение. Величина k = b / a называется коэффициентом сжатия эллипса, а величина 1 – k = ( a – b )/ a называется сжатием эллипса.

Коэффициент сжатия и эксцентриситет связаны соотношением: k 2 = 1 – e 2 .

Если a = b ( c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.

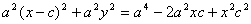
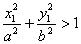
Если для точки М( х₁, у₁) выполняется условие: , то она находится внутри эллипса, а если , то точка находится вне эллипса.

Теорема. Для произвольной точки М( х , у), принадлежащей эллипсу верны соотношения:

r ₁ = a – ex , r ₂ = a + ex .

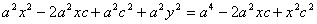
Доказательство. Выше было показано, что r ₁ + r ₂ = 2 a . Кроме того, из геометрических соображений можно записать:

После возведения в квадрат и приведения подобных слагаемых:

Аналогично доказывается, что r ₂ = a + ex . Теорема доказана.

С эллипсом связаны две прямые, называемые директрисами. Их уравнения:

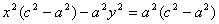
x = a / e ; x = — a / e .

Теорема. Для того , чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.

Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса, заданного уравнением:

1) Координаты нижней вершины: x = 0; y 2 = 16; y = -4.

2) Координаты левого фокуса: c 2 = a 2 – b 2 = 25 – 16 = 9; c = 3; F ₂ (-3; 0).

3) Уравнение прямой, проходящей через две точки:

Пример. Составить уравнение эллипса, если его фокусы F ₁ (0; 0), F ₂ (1; 1), большая ось равна 2.

Уравнение эллипса имеет вид: 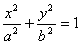. Расстояние между фокусами:

2 c = , таким образом, a 2 – b 2 = c 2 = ½

по условию 2а = 2, следовательно а = 1, b =

Итого: .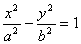

Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.

y

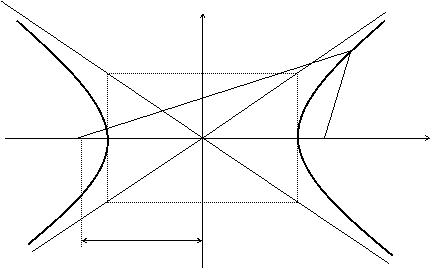
По определению ï r ₁ – r ₂ ï = 2 a . F ₁ , F ₂ – фокусы гиперболы. F ₁ F ₂ = 2 c .

Выберем на гиперболе произвольную точку М( х , у). Тогда :

обозначим с 2 – а 2 = b 2 (геометрически эта величина – меньшая полуось)

Получили каноническое уравнение гиперболы.

Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.

Ось 2а называется действительной осью гиперболы.

Ось 2 b называется мнимой осью гиперболы.

Гипербола имеет две асимптоты, уравнения которых

Определение. Отношение 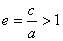называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.

С учетом того, что с 2 – а 2 = b 2 :

Если а = b , e = , то гипербола называется равнобочной (равносторонней).

Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a / e от него, называются директрисами гиперболы. Их уравнения: .

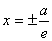
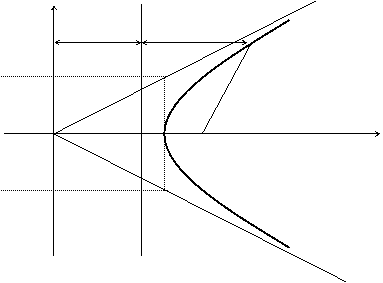
Теорема. Если r – расстояние от произвольной точки М гиперболы до какого — либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r / d – величина постоянная, равная эксцентриситету.

Доказательство. Изобразим схематично гиперболу.

y

Видео:№966. Напишите уравнение окружности радиуса r с центром А, если: а) А(0;5), r= 3; б) А(-1;2), r = 2Скачать

Парабола

Параболой называется геометрическое место точек, для каждой из кото­рых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называе­мой директрисой. Фокус параболы обозначается буквой F, расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.

Пусть дана некоторая парабола. Введём декартову прямоугольную си­стему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посредине между фокусом и дире­ктрисой (черт. 19). В этой системе координат данная парабола будет опреде­ляться уравнением

Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение

х = — .

Фокальный радиус произвольной точки М(х; у) параболы (т. е. длина от­резка FM) может быть вычислен по формуле

r = x +

Парабола имеет одну ось симметрии, называемую осью параболы, с ко­торой она пересекается в единственной точке. Точка пересечения параболы

Черт. 19. Черт. 20.

с осью называется её вершиной. При указанном выше выборе координатной системы ось параболы совмещена с осью абсцисс, вершина находится в на­чале координат, вся парабола лежит в правой полуплоскости.

Черт. 21. Черт. 22.

Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в ле­вой полуплоскости (черт. 20), то её уравнение будет иметь вид

В случае, когда начало координат находится в вершине, а с осью сов­мещена ось ординат, парабола будет иметь уравнение

если она лежит в верхней полуплоскости (черт. 21), и

— если в нижней полуплоскости (черт. 22).

Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), назы­вается каноническим.

583. Составить уравнение параболы, вершина которой находится в начале координат, зная, что:

1) парабола расположена в правой полуплоскости, симметрично относительно оси Ох, и её параметр р = 3;

2) парабола расположена в левой полуплоскости, симметрично относительно оси Ох, и её параметр р = 0,5;

3) парабола расположена в верхней полуплоскости, симметрично относительно оси Оу, и её параметр p = ;

4) парабола расположена в нижней полуплоскости, симметрично относительно оси Оу, и её параметр р =3.

584. Определить величину параметра и расположение относи­тельно координатных осей следующих парабол:

585. Составить уравнение параболы, вершина которой находится в начале координат, зная, что:

1) парабола симметрично расположена относительно оси Ох и проходит через точку А (9; 6);

2) парабола симметрично расположена относительно оси Ох и проходит через точку В(—1; 3);

3) парабола симметрично расположена относительно оси Оу и проходит через точку С(1; 1);

4) парабола симметрично расположена относительно оси Оу и проходит через точку D (4; — 8).

586. Стальной трос подвешен за два конца; точки крепления расположены на одинаковой высоте; расстояние между ними равно 20 м. Величина его прогиба на расстоянии 2 м от точки крепления, считая по горизонтали, равна 14,4 см. Определить величину прогиба этого троса в середине между точками крепления, приближённо считая, что трос имеет форму дуги параболы.

587. Составить уравнение параболы, которая имеет фокус F(0; —3) и проходит через начало координат, зная, что её осью служит ось Оу.

588. Установить, какие линии определяются следующими урав­нениями:

1) у = + 2, 2) у = +, 3) у = — 3,

4) у = — 2, 5) х = + , 6) х = — 5,

7) х = — , 8) х = + 4.

Изобразить эти линии на чертеже.

589. Найти фокус F и уравнение директрисы параболы у2 = 24х.

590. Вычислить фокальный радиус точки М параболы у2 = 20х, если абсцисса точки М равна 7.

591. Вычислить фокальный радиус точки М параболы у2=12х, если ордината точки М равна 6.

592. На параболе уа=16х найти точки, фокальный радиус которых равен 13.

593. Составить уравнение параболы, если дан фокус F(— 7; 0) и уравнение директрисы х—7 = 0.

594. Составить уравнение параболы, зная, что её вершина совпа­дает с точкой (а; 3), параметр равен р, ось параллельна оси Ох и парабола простирается в бесконечность:

1) в положительном направлении оси Ох;

2) в отрицательном направлении оси Ох.

595 . Составить уравнение параболы, зная, что её вершина совпа­дает с точкой (а; (3), параметр равен р, ось параллельна оси Оу и парабола простирается в бесконечность:

1) в положительном направлении оси Оу (т. е. парабола является восходящей);

2) в отрицательном направлении оси Оу (т. е. парабола является нисходящей).

596. Установить, что каждое из следующих уравнений определяет параболу, и найти координаты её вершины А, величину параметра р и уравнение директрисы:

597. Установить, что каждое из следующих уравнений опреде­ляет параболу, и найти координаты её вершины А и величину параметра р:

1) y = х2 + х + 2, 2) y = 4x2 — 8x + 7,

3) y = — х2 + 2х— 7.

698. Установить, что каждое из следующих уравнений опреде­ляет параболу, и найти координаты её вершины А и величину параметра р:

1) х = 2у2 — 12у + 14, 2) х = — у2 + у,

599. Установить, какие линии определяются следующими уравне­ниями:

1) у = 3 — 4, 2) х = — 4 + 3,

3) х = 2 — , 4) у = — 5 — .

Изобразить эти линии на чертеже.

600. Составить уравнение параболы, если даны её фокус F(7; 2) и директриса х — 5 = 0.

601. Составить уравнение параболы, если даны её фокус F(4; 3) и директриса у + 1 = 0.

602. Составить уравнение параболы, если даны её фокус F(2; —1) и директриса х — у — 1 = 0.

603. Дана вершина параболы А (6; —3) и уравнение ее дире­ктрисы

Найти фокус F этой параболы.

604. Дана вершина параболы А(—2; —1) и уравнение её ди­ректрисы

Составить уравнение этой параболы.

605. Определить точки пересечения прямой х + у— 3 = 0, и параболы х2 = 4у.

606. Определить точки пересечения прямой 3х + 4у—12 = 0 и параболы у2 = — 9х.

607. Определить точки пересечения прямой 3х — 2у + 6 = 0 и параболы у2 = 6х.

608. В следующих случаях определить, как расположена данная прямая относительно данной параболы — пересекает ли, касается или проходит вне её:

609. Определить, при каких значениях углового коэффициента k

прямая у = Ах + 2:

1) пересекает параболу у2 = 4х;

3) проходит вне этой параболы.

610. Вывести условие, при котором прямая y = kx + b касается параболы у2 = 2рх.

611. Доказать, что к параболе у2 = 2рх можно провести одну и только одну касательную с угловым коэф­фициентом k ≠ 0.

612. Составить уравнение касательной к параболе у2 = 2рх в её точке М1(х1; у1)

613. Составить уравнение прямой, которая касается пара­болы у2 = 8х и параллельна прямой

614. Составить уравнение прямой, которая касается пара­болы х2=16у и перпендикулярна к прямой

615. Провести касательную к параболе у2=12х параллельно прямой

и вычислить расстояние d между этой касательной и данной прямой.

616. На параболе у2 = 64х найти точку М1 ближайшую к прямой

и вычислить расстояние d от точки М1 до этой прямой.

617. Составить уравнения касательных к параболе у2 = 36х, проведённых из точки А (2; 9).

618. К параболе у2 = 2рх проведена касательная. Доказать, что вершина этой параболы лежит посредине между точкой пересечения касательной с осью Ох и проекцией точки касания на ось Ох.

619. Из точки А (5; 9) проведены касательные к параболе y2 = 5х. Составить уравнение хорды, соединяющей точки касания.

620. Из точки Р(—3; 12) проведены касательные к параболе

Вычислить расстояние d от точки Р до хорды параболы, соеди­няющей точки касания.

621. Определить точки пересечения эллипса па­раболы у2 = 24х.

622. Определить точки пересечения гиперболы

623. Определить точки пересечения двух парабол:

624. Доказать, что прямая, касающаяся параболы в некоторой точке М, составляет равные углы с фокальным радиусом точки М и с лучом, который, исходя из М, идёт параллельно оси параболы в ту сторону, куда парабола бесконечно простирается.

625. Из фокуса параболы

под острым углом а к оси Ох направлен луч света. Известно, что 3 tgα = . Дойдя до параболы, луч от неё отразился. Составить

уравнение прямой, на которой лежит отражённый луч.

626. Доказать, что две параболы, имеющие общую ось и общий фокус, расположенный между их вершинами, пересекаются под пря­мым углом.

627. Доказать, что если две параболы со взаимно перпендику­лярными осями пересекаются в четырёх точках, то эти точки лежат на одной окружности.

Видео:№971. Напишите уравнение окружности, проходящей через точки А (-3; 0) и B (0; 9), если известноСкачать

Записать уравнение окружности, проходящей через указанные точки и имеющий центр в точке А

Вершины гиперболы 12x^2-13y^2=156

Ответ
Уравнение окружности с центром в начале координат:
x^2 + y^2 = R^2
Уравнение окружности с центром в точке А (x1; y1) будет:
(x — x1)^2 + (y — y1)^2 = R^2
Решай.

🌟 Видео

9 класс, 7 урок, Уравнение прямойСкачать

№972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать

КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Как легко составить уравнение параболы из графикаСкачать

Составляем уравнение прямой по точкамСкачать

УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Составляем уравнение окружностиСкачать

Уравнение окружностиСкачать

№969. Напишите уравнение окружности с диаметром MN, если: а) М (-3; 5),Скачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать