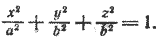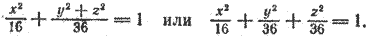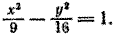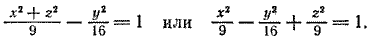P.S. Все хотела спросить, а где оставшиеся вввв (в нике имеется в виду)?
Значит, если нужно крутить вокруг какой-нибудь оси, скажем оси Ох, другими словами икс оставить в покое, а другое заменить на sqrt(y^2+z^2) т.е. иксы не будут входить под радикал. А если такое y^3=2x, и в такой ситуации это правило работает?
Дааа, какое хорошее правило, обязательно запомню. А для полярных координат, нет такого правила, или для параметрически заданной линии?
Видео:Поверхности второго порядкаСкачать

Задача 62549 Записать уравнение и определить вид.
Условие
Записать уравнение и определить вид поверхности, полученной при вращении
данной линии вокруг указанной оси координат, сделать рисунок.
a) 4x^2-3y^2=12 Ox
б) x=1, y=2 Oz
Решение
a) 4x^2–3y^2=12
делим на 12
(x^2/3)-(y^2/4)=1
при вращении
данной линии вокруг оси Ox
В плоскости xОz
(x^2/3)-(z^2/4)=1
⇒ значит поверхность имеет вид:
(x^2/3)-(y^2/4)-(z^2/4)=1- двуполостный гиперболоид
б) x=1, y=2 ⇒ пара взаимно перпендикулярных прямых ( см. рис.2)
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Записать уравнение и определить вид поверхности полученной при вращении данной линии
Глава VI. Простейшие криволинейные поверхности и тела вращения.
§ 75*. Поверхности вращения
1. Пусть в плоскости р задана кривая L и некоторая прямая l. Поверхность, которая получается вращением кривой L вокруг прямой l, называется поверхностью вращения.
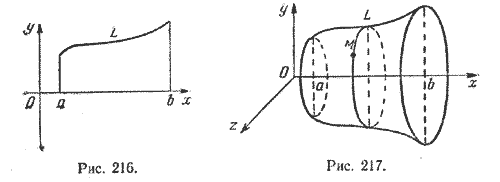
Пусть кривая L лежит в плоскости хОу (рис. 216) и имеет уравнение
y = f(x), х 
Найдем уравнение поверхности, которая получится вращением кривой L вокруг оси Ох (рис. 217).
Очевидно, точка M с координатами (х; у; z), где х 
Действительно, точки (х; у; z) и (х; f(x); 0) лежат на одной окружности с центром в точке (х; 0; 0).
Таким образом, уравнение поверхности, полученной вращением кривой (1) вокруг оси Ох, имеет вид
y 2 + z 2 = (f(x)) 2 , х 
Заметим, что уравнение (2) получается из уравнения (1) следующим образом:
обе части уравнения (1) возводятся в квадрат и y 2 заменяется на y 2 + z 2 ,
В частности, если кривая L задана уравнением
то уравнение поверхности, полученной вращением этой кривой вокруг оси Ох, имеет вид
т. е. просто y 2 заменяем на y 2 + z 2 .
2. Поверхность, которая получается вращением эллипса вокруг одной из его осей, называется эллипсоидом вращения.
Пусть в плоскости хОу эллипс задан уравнением
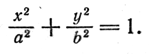
Составим уравнение поверхности, полученной вращением его вокруг оси Ох. Уравнение эллипса (5) приводится к виду (3), следовательно, для получения уравнения эллипсоида вращения достаточно в уравнении (5) y 2 заменить на y 2 + z 2 . После замены получим
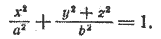
Это уравнение обычно записывают так:
При а > b уравнение (6) определяет эллипсоид вращения, вытянутый вдоль оси Ох (рис. 218), при а 2 на y 2 + z 2 , получим искомое уравнение эллипсоида вращения:
3. Поверхность, которая получается вращением гиперболы вокруг одной из ее осей, называется гиперболоидом вращения. При вращении гиперболы вокруг ее действительной оси получается двуполостный гиперболоид вращения (рис. 220), а при вращении гиперболы вокруг ее мнимой оси получается однополостный гиперболоид вращения (рис. 221).
Пусть в плоскости хОу гипербола задана уравнением
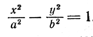
Составим уравнение поверхности, полученной вращением гиперболы вокруг ее действительной оси Ох. Уравнение гиперболы (7) приводится к виду (3); следовательно, для получения уравнения поверхности двуполостного гиперболоида вращения достаточно в уравнении гиперболы (7) y 2 заменить на y 2 + z 2 . После замены получим
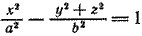
При вращении гиперболы (7) вокруг ее мнимой оси нужно в уравнении (7) x 2 заменить на x 2 + z 2 ; после замены получим
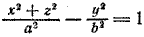
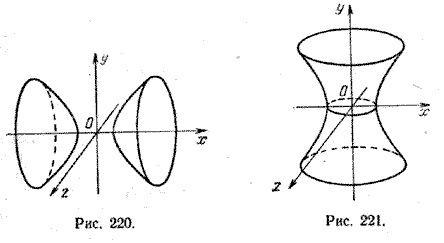
Задача 2. Гипербола с полуосями а = 3 и b = 4 вращается вокруг своей мнимой оси, совпадающей с осью Оу. Центр гиперболы совпадает с началом координат. Составить уравнение поверхности, полученной при вращении этой гиперболы.
Составим уравнение гиперболы:
Чтобы получить уравнение гиперболоида вращения, в уравнении гиперболы x 2 заменим на x 2 + z 2 . После замены получим
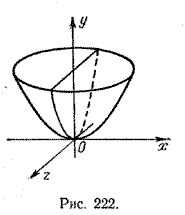
4. Поверхность, которая получается вращением параболы вокруг ее оси симметрии, называется параболоидом вращения (рис. 222).
Пусть на плоскости хОу парабола задана уравнением
Для получения уравнения поверхности вращения нужно в уравнении (10) x 2 заменим на x 2 + z 2 ; после замены получим
Отметим одно замечательное свойство этой поверхности. Если внутреннюю поверхность параболоида вращения сделать зеркальной, а в ее фокусе (фокусом параболоида вращения называется фокус вращаемой параболы) поместить источник света, то все лучи света, отражаясь от поверхности параболоида, пойдут параллельно оси параболоида.
Это свойство широко используется при изготовлении светоотражающих устройств (прожекторов, фар автомобиля, кинопроекторов и других приборов).
Задача 3. Составить уравнение поверхности, полученной вращением параболы y 2 = 2х вокруг оси Ох.
Чтобы составить уравнение параболоида вращения, полученного вращением параболы вокруг оси Ох, нужно в уравнении y 2 = 2х заменить y 2 на y 2 + z 2 , после замены получим
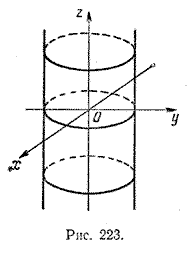
5. Если вращать прямую, параллельную какой-либо оси координат, вокруг этой оси, то получится круговая цилиндрическая поверхность.
Пусть дана прямая, лежащая в плоскости yOz и имеющая уравнение у = а. Легко видеть, что поверхность вращения этой прямой вокруг оси Oz имеет уравнение
Эта цилиндрическая поверхность изображена на рис. 223.
Задача 4. Составить уравнение цилиндрической поверхности, полученной вращением прямой у = 3, лежащей в плоскости хОу вокруг оси Ох.
В уравнении y 2 = 3 2 заменим y 2 на y 2 + z 2 , в результате получим
6. Пусть дана прямая, лежащая в плоскости yOz и проходящая через начало координат:
y = kz, k =/= 0.
Очевидно, уравнение поверхности вращения этой прямой вокруг оси Oz имеет вид
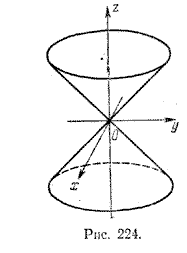
Полученное уравнение является уравнением искомой поверхности вращения, которая называется круговой конической поверхностью (рис. 224).
Задача 5. Составить уравнение поверхности вращения прямой 2х = 3у, z =0 вокруг оси Ох.
Из уравнения 3у = 2х, используя формулу (2), находим 9(y 2 + z 2 ) = 4x 2 . Это и есть искомое уравнение.
🔍 Видео
§64 Поверхности вращенияСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

Поверхности второго порядка. Поверхности вращенияСкачать
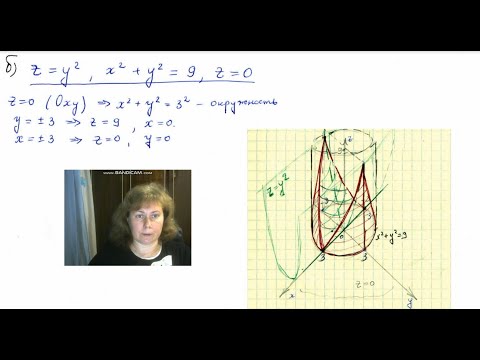
Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

§65 ЭллипсоидСкачать
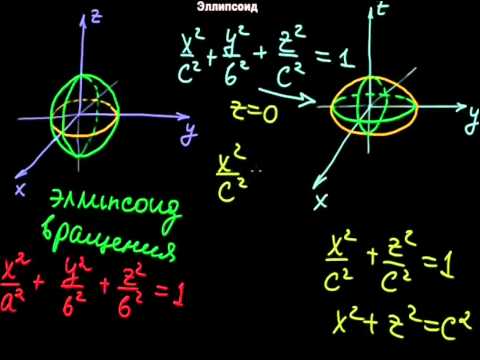
СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Линия пересечения двух поверхностей вращения (Метод вспомогательных сфер)Скачать

Составляем уравнение прямой по точкамСкачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

9 класс, 6 урок, Уравнение окружностиСкачать

Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать

Приведение поверхности второго порядка к каноническому виду ортогональным преобразованием.Скачать

Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Семинар 6. Приведение уравнения кривой II порядка к каноническому видуСкачать

Видеоурок "Нормальное уравнение прямой"Скачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать