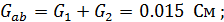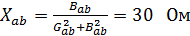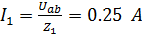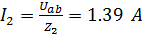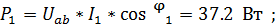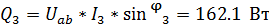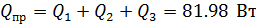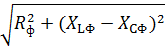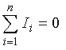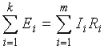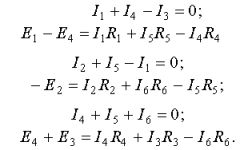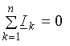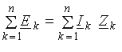Содержание:

Законы Кирхгофа

Уравнения, описывающие поведение электрической цепи, составляют на основе законов Кирхгофа. Они определяют связь между токами и напряжениями элементов, образующих цепь. Уравнения, составленные согласно этим законам, называют уравнениями Кирхгофа.

Первый закон Кирхгофа определяет баланс токов в узлах электрической цепи.

Он формулируется следующим образом:

Алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю:

В уравнении (3.1) токи, направленные от узла, записывают с положительным знаком. Токи, направленные к узлу, записывают со знаком минус.

Система уравнений по первому закону Кирхгофа, записанная для всех узлов цепи, линейно зависима. В этом легко убедиться, сложив все уравнения. Поскольку ток каждой ветви входит в два уравнения с разными знаками, сумма тождественно равна нулю. Поэтому число независимых уравнений по первому закону Кирхгофа равно , где — число узлов цепи.

Второй закон Кирхгофа устанавливает баланс напряжений в контуре цепи:

Алгебраическая сумма напряжений ветвей в контуре равна нулю:

Если напряжение ветви совпадает с направлением обхода контура, то напряжению приписывают знак плюс, если же нет — знак минус. Перенесем напряжения источников напряжения, равные ЭДС этих источников, в правую часть. Уравнение (3.2) примет вид

В соответствии с последним равенством алгебраическая сумма напряжений ветвей в контуре электрической цепи равна алгебраической сумме ЭДС источников.

Число независимых уравнений, записанных по второму закону Кирхгофа, равно числу независимых контуров. Число таких контуров определяется формулой , где — число ветвей.

Возможно вам будут полезны данные страницы:

Порядок составления уравнений но законам Кирхгофа

1. Необходимо сначала выбрать положительные направления токов и напряжений ветвей. Положительное направление тока показывают стрелкой на выводе элемента. Положительное направление напряжения показывают стрелкой, расположенной рядом с элементом. Полярности напряжений резисторов выбирают согласованными с направлениями токов. Направления токов источников напряжения выбирают совпадающими с направлениями ЭДС.

2. Записываем уравнения по первому закону Кирхгофа для узлов.

3. Выбираем направления обхода контуров и записываем уравнения по законам Кирхгофа. Сопротивление проводника, соединяющего элементы, очень мало по сравнению с сопротивлением резистора и игнорируется. Ячейки внутренней цепи удобно выбирать в качестве независимых цепей. Можно воспользоваться и другим способом: выбрать по порядку контуры, так, чтобы каждый следующий контур содержал, по меньшей мере, одну ветвь, не входящую в предыдущие контуры.

4. Решаем полученную систему уравнений и определяем токи и напряжения цепи.

5. После определения токов и напряжений необходимо выполнить проверку. Для этого вычисленные значения переменных подставляют в одно из уравнений, составленных по законам Кирхгофа.

При составлении уравнений в качестве неизвестных рассматривают либо токи, либо напряжения резистивных элементов.

В первом случае уравнения цепи составляют относительно неизвестных токов резистивных элементов и напряжений на источниках тока. Напряжения на резистивных элементах, входящие в уравнения по второму закону Кирхгофа, выражают через токи по закону Ома. Такой способ составления уравнений называют токов ветвей.

Число совместно решаемых уравнений в методе токов ветвей можно сократить, если контуры выбирать так, чтобы они не включали источники тока. В этом случае неизвестными будут только токи резистивных элементов, и по второму закону Кирхгофа достаточно составить уравнений, где — количество источников тока.

Во втором случае уравнения цепи составляются относительно напряжений резистивных элементов и токов источников напряжения. Токи резисторов представляют произведением проводимости на напряжение на резисторе. Этот способ составления уравнений называют методом напряжений ветвей.

В дальнейшем для решения задач мы будем использовать в основном метод токов ветвей.

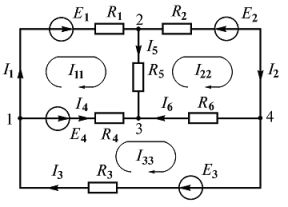
Пример 3.1. Записать уравнения Кирхгофа для цепи, показанной на рис. 3.1.

Решение. Сначала выберем направления токов резистивных элементов и пронумеруем узлы. Неизвестными являются токи резистивных элементов . Поэтому необходимо составить пять уравнений. Цепь содержит четыре узла; это означает, что по первому закону Кирхгофа можно составить три уравнения. Число уравнений по второму закону Кирхгофа равно двум.

Запишем уравнения по первому закону Кирхгофа для узлов 1, 2, 3. Контуры I и II выберем так, чтобы они не включали источник тока, иначе в системе уравнений появится дополнительная переменная — напряжение источника тока. Направления обхода контуров выберем совпадающими с направлением движения часовой стрелки. В результате получим систему из пяти уравнений с пятью неизвестными токами:

Узел 1: ;

Узел 2: ;

Узел З: ;

Контур I:

Контур II:

Для решения системы уравнений целесообразно использовать математические пакеты, например MathCAD или Matlab.

Напряжение на зажимах источника тока можно затем найти, записав уравнения для контуров, включающих или

Пример задачи с решением 3.2.

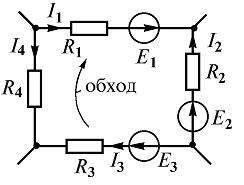
Рассчитать токи в цепи, изображенной на рис. 3.2. Номиналы элементов: ,

Решение. Сначала выберем направления токов резистивных элементов и пронумеруем узлы. В рассматриваемой схеме шесть неизвестных токов , следовательно, необходимо составить шесть независимых уравнений. Цепь содержит четыре узла; это означает, что по первому закону Кирхгофа можно составить три уравнения. Еще три уравнения составим по второму закону Кирхгофа. Наличие источника тока учитывалось при определении числа уравнений по второму закону Кирхгофа.

Составим уравнения по первому закону Кирхгофа для узлов 1, 2 и 3. Уравнения по второму закону Кирхгофа запишем для контуров I, II, III. Направление обхода контуров выбираем по часовой стрелке.

В результате получим систему из шести уравнений с шестью неизвестными токами:

В матричной форме записи:

Решением системы уравнений являются следующие значения токов:

Знак минус в численных значениях токов означает, что направление токов при заданных условиях выбрано навстречу истинному.

На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).

Услуги:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Как составить уравнения по законам Кирхгофа?Скачать

Записать систему уравнений по законам кирхгофа в дифференциальной и символической формах

Задача 1.2. Линейные электрические цепи cинусоидального тока

Для электрической схемы, соответствующей номеру варианта и изображенной на рис., выполнить следующее:

1. На основании законов Кирхгофа составить в общем виде систему уравнений для расчета токов во всех ветвях цепи, записав её в двух формах:
   1. дифференциальной;
   2. символической.
2. Определить комплексы действующих значений токов во всех ветвях, воспользовавшись одним из методов расчета линейных электрических цепей.
3. По результатам, полученным в п.2, определить показание ваттметра.
4. Построить топографическую диаграмму, совмещенную с векторной диаграммой токов, потенциал точки a, указанной на схеме, принять равным нулю.
5. (Факультативный) Построить круговую диаграмму для тока в одном из сопротивлений цепи при изменении модуля этого сопротивления в пределах от 0 до ∞. Сопротивление, подлежащее изменению, отмечено на схеме стрелкой.
6. (Факультативный) Пользуясь круговой диаграммой, построить график изменения тока в изменяющемся сопротивлении в зависимости от модуля этого сопротивления.

1. Используя данные расчетов, полученных в пп. 2, 5, записать выражение для мгновенного значения тока или напряжения (см. указание к выбору варианта). Построить график зависимости указанной величины от ωt.
2. Полагая, что между двумя любыми индуктивными катушками, расположенными в различных ветвях заданной схемы, имеется магнитная связь при взаимной индуктивности, равной M, составить в общем виде систему уравнений по законам Кирхгофа для расчета токов во всех ветвях схемы, записав её в двух формах:
   1. дифференциальной;
   2. символической.

Видео:Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Составим, на основании законов Кирхгофа, систему уравнений для расчета токов во всех ветвях цепи и запишем ее в дифференциальной и символической формах

В символической форме:

Подставив численные значения, получим:

Определим комплексы действующих значений токов, воспользовавшись символическим методом расчета. Запишем выражения для мгновенных значений токов.

Данная цепь является простой разветвленной, она может быть решена методом свертывания. Определим Z эквивалентное:

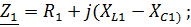
Подставив численные значения, получим:

;

Определим ток в неразветвленной части цепи.

Определим напряжение на зажимах а, в.

Определим токи в параллельных ветвях.

3) Составим баланс мощностей в комплексной форме, выполнив соответствующие вычисления.

Классический метод.

Определим эквивалентную проводимость параллельных ветвей.

Определим эквивалентные сопротивления ветви а,в.

Град

Определим эквивалентное сопротивление.

;

Определим ток в неразветвленной части ветви и угол между ЭДС E₃ и током I₃.

;

Определим напряжение на зажимах а b.

Определим токи в параллельных ветвях и углы ᵠ.

;

;

Рассчитаем погрешность при расчете активной мощности:

– в допустимых

Рассчитаем погрешность при расчете реактивной мощности:

– в допустимых пределах.

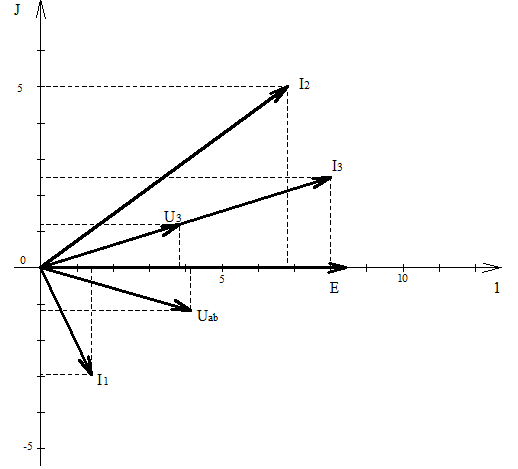
4)Построим на комплексной плоскости векторную диаграмму напряжений и токов.

В трехфазной системе нагрузка соединена в звезду с нейтральным проводом. Определить:

1. Фазные и линейные токи.

2. Угол сдвига фаз между током и напряжением в каждой фазе.

3. Активную, реактивную и полную мощность потребляемую системой.

При обрыве фазы А определить режимы в остальных двух фазах при наличие нейтрального провода и без него.

Для всех случаев построить векторные диаграммы.

Объединение в одну цепь нескольких подобных по структуре цепей синусоидального тока одной частоты с независимыми источниками энергии широко применяются в технике. Объединяемые цепи синусоидального тока принято называть фазами, а всю объединенную систему цепей – многофазной системой. Для получения трехфазной системы необходимо определенным образом соединить фазы источника энергии и приемника. Возможны два способа соединения в трехфазной системе – соединение фаз источника и приемника звездой и треугольником.

Изобразим схему трехфазной системы объединенную в звезду.

Определяем фазные и линейные токи.

U_L= =381В
полное сопротивление в фазе: Z_Ф=

Z_Ф= 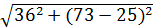=60 Ом

Законы Кирхгофа — формулы и примеры использования

Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа. Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах.

Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.

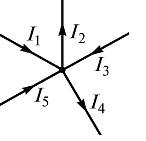
где – число токов, сходящихся в данном узле. Например, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 — I2 + I3 — I4 + I5 = 0

В этом уравнении токи, направленные к узлу, приняты положительными.

Физически первый закон Кирхгофа – это закон непрерывности электрического тока.

Второй закон Кирхгофа: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре

где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii , Ri – ток и сопротивление i -й ветви.

Так, для замкнутого контура схемы (рис. 2 ) Е1 — Е2 + Е3 = I1R1 — I2R2 + I3R3 — I4R4

Замечание о знаках полученного уравнения:

1) ЭДС положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;

2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода.

Физически второй закон Кирхгофа характеризует равновесие напряжений в любом контуре цепи.

Расчет разветвленной электрической цепи с помощью законов Кирхгофа

Метод законов Кирхгофа заключается в решении системы уравнений, составленных по первому и второму законам Кирхгофа.

Метод заключается в составлении уравнений по первому и второму законам Кирхгофа для узлов и контуров электрической цепи и решении этих уравнений с целью определения неизвестных токов в ветвях и по ним – напряжений. Поэтому число неизвестных равно числу ветвей b , следовательно, столько же независимых уравнений необходимо составить по первому и второму законам Кирхгофа.

Число уравнений, которые можно составить на основании первого закона, равно числу узлов цепи, причем только ( y – 1) уравнений являются независимыми друг от друга.

Независимость уравнений обеспечивается выбором узлов. Узлы обычно выбирают так, чтобы каждый последующий узел отличался от смежных узлов хотя бы одной ветвью. Остальные уравнения составляются по второму закону Кирхгофа для независимых контуров, т.е. число уравнений b — (y — 1) = b — y +1 .

Контур называется независимым, если он содержит хотя бы одну ветвь, не входящую в другие контуры.

Составим систему уравнений Кирхгофа для электрической цепи (рис. 3 ). Схема содержит четыре узла и шесть ветвей.

Поэтому по первому закону Кирхгофа составим y — 1 = 4 — 1 = 3 уравнения, а по второму b — y + 1 = 6 — 4 + 1 = 3 , также три уравнения.

Произвольно выберем положительные направления токов во всех ветвях (рис. 4 ). Направление обхода контуров выбираем по часовой стрелке.

Составляем необходимое число уравнений по первому и второму законам Кирхгофа

Полученная система уравнений решается относительно токов. Если при расчете ток в ветви получился с минусом, то его направление противоположно принятому направлению.

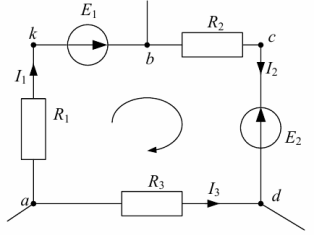
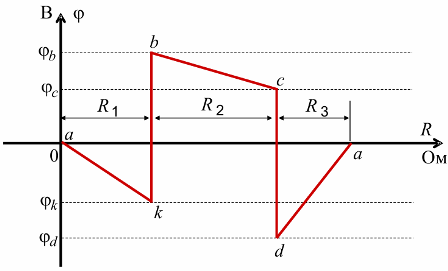
Рассмотрим контур abcda схемы, изображенной на рис. 4. В ветке ab между резистором R1 и ЭДС E1 обозначим дополнительную точку k.

Рис. 4. Контур для построения потенциальной диаграммы

Потенциал любого узла принимаем равным нулю (например, ?а= 0), выбираем обход контура и определяем потенциалы точек контура: ?а = 0, ?к = ?а — I1R1 , ? b = ? к + Е1, ?с = ? b — I2R2 , ? d = ?c — Е2, ? a = ?d + I3R3 = 0

При построении потенциальной диаграммы необходимо учитывать, что сопротивление ЭДС равно нулю (рис. 5 ).

Рис. 5. Потенциальная диаграмма

Законы Кирхгофа в комплексной форме

Для цепей синусоидального тока законы Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений.

Первый закон Кирхгофа : «алгебраическая сумма комплексов тока в узле электрической цепи равна нулю»

Второй закон Кирхгофа : «в любом замкнутом контуре электрической цепи алгебраическая сумма комплексных ЭДС равна алгебраической сумме комплексных напряжений на всех пассивных элементах этого контура».

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Не пропустите обновления, подпишитесь на наши соцсети:

💥 Видео

Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Расчет переходного процесса через ДИФФЕРЕНЦИАЛЬНОЕ уравнение по законам Кирхгофа│Классический методСкачать

Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать

Применение законов Кирхгофа при решении задачСкачать

Законы Кирхгофа - самое простое и понятное объяснение этих законовСкачать

ТОЭ 32. Законы Кирхгофа в символической форме. Действия с комплексами.Скачать

Расчет цепи по законам КирхгофаСкачать

Урок 265. Задачи на правила КирхгофаСкачать

Законы Кирхгофа. Метод контурных уравненийСкачать

решение задачи составлением уравнений по правилам киргофа. Законы киргофа кратко на практикеСкачать

Лекция 117. Правила КирхгофаСкачать

2 8 Метод непосредственного применения законов КирхгофаСкачать

Правила Кирхгофа - определение токов. ЭлектротехникаСкачать

Цепи переменного тока. Найти токи в цепи по законам КирхгофаСкачать

Лекция по электротехнике 2.5 - Составление уравнений КирхгофаСкачать

Правила Кирхгофа: пример расчёта цепи с источниками токаСкачать

021 Расчет электрической цепи по законам КирхгофаСкачать

Метод узловых и контурных уравненийСкачать