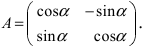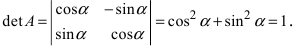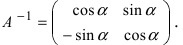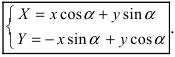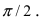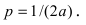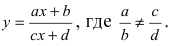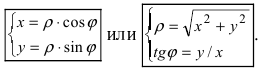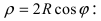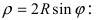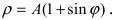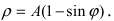Записать преобразование параллельного переноса приводящее уравнение к каноническому виду (7 видео)

Приведение кривой второго порядка к каноническому виду

Пример №1 . Привести уравнение второго порядка к каноническому виду с помощью поворота и параллельного переноса осей координат. Построить кривую.

Пример №2 . Выполнив последовательно преобразования координат: поворот, а затем параллельный перенос координатных осей, преобразовать к каноническому виду уравнение кривой второго порядка и построить ее в исходной системе координат, а также найти параметры кривой.

Содержание

Алгоритм перехода кривой второго порядка к каноническому виду
Преобразования декартовой системы координат с примерами решения
Преобразования декартовой системы координат
Параллельный перенос и поворот системы координат
Полярные координаты. Замечательные кривые
📸 Видео

Видео:Приведение кривой второго порядка к каноническому виду. ПримерСкачать

Алгоритм перехода кривой второго порядка к каноническому виду

Пример №1 . 4y=-6-sqrt(4x-x 2 )
sqrt(4x-x 2 ) = -(4y+6)
Возведем в квадрат
4x-x 2 = (4y+6) 2
Раскрывая скобки, получаем:
16y 2 +48y + 36 +x 2 -4x = 0

Далее решается калькулятором. Если самостоятельно решать, то получим:
4x-x 2 = (4y+6) 2
-(x 2 — 4x) = 2(y+3/2) 2
-(x 2 — 4x + 4) = (y+3/2) 2
-(x — 2) 2 = (y+3/2) 2
(y+3/2) 2 + (x — 2) 2 = 0

Пример №2 . x=1-2/3 sqrt(y 2 -4y-5)
Здесь надо сначала привести к нормальному виду.
3/2(x-1)=sqrt(y 2 -4y-5)
Возводим в квадрат
9/4(x-1) 2 =y 2 -4y-5
9/4x 2 -9/4*2x+9/4-y 2 +4y+5=0
9/4x 2 -9/2x-y 2 +4y+29/4=0

Далее можно решать как с калькулятором, так и без него:
9/4(x-1) 2 =y 2 -4y-5
9/4(x-1) 2 =y 2 -4y+4-4-5
9/4(x-1) 2 =(y 2 -2)-9
9/4(x-1) 2 -(y 2 -2) = -9
-1/4(x-1) 2 +1/9(y 2 -2) = 1

Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Преобразования декартовой системы координат с примерами решения

Содержание:

Видео:Поворот и параллельный перенос координатных осей. ЭллипсСкачать

Преобразования декартовой системы координат

Параллельный перенос и поворот системы координат

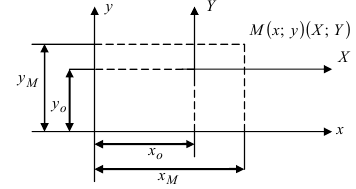
1. Параллельный перенос системы координат. Пусть на плоскости две декартовы системы координат, причем соответствующие оси параллельны и сонаправлены (Рис.46):

Рис. 46. Параллельный перенос одной системы координат относительно другой системы.

Систему координат

Пример:

Дана точка М(3;2) и начало новой системы координат 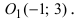Вычислить положение точки М в новой системе отсчета.

Решение:

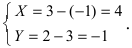
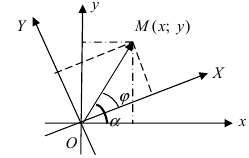
Используя формулы, определяющие параллельный перенос одной системы отсчета относительно другой, получим Следовательно, точка М в новой системе отсчета имеет координаты М(4; -1).

2. Поворот системы координат. Пусть даны две системы координат (старая и новая), имеющие общее начало отсчета и повернутые относительно друг друга на угол 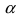(Рис. 47):

Рис. 47. Поворот одной системы координат относительно другой системы с общим началом координат двух систем.

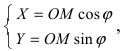
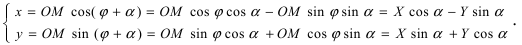
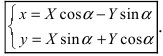
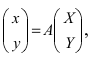
Получим формулы, связывающие старые и новые координаты произвольной точки М(х; у). Из рисунка видно, что в новой системе координат координаты точки равны а координаты этой точки в старой системе координат равны Таким образом формулы перехода от новых координат произвольной точки М к старым имеет вид В матричном виде эти равенства можно записать в виде где матрица перехода

Найдем обратное преобразование системы координат, найдем матрицу 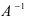обратную к матрице А:

Найдем алгебраические дополнения всех элементов

Запишем обратную матрицу

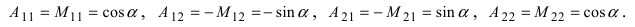
Определение: Унитарными преобразованиями называются такие преобразования, для которых определитель матрицы преобразования равен 1.

Определение: Ортогональными преобразованиями называются такие преобразования, для которых обратная матрица к матрице преобразования совпадает с транспонированной матрицей преобразования.

Таким образом, имеем 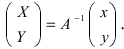Следовательно, формулы перехода от старой системы отсчета к новой системе отсчета имеют вид:

Пример:

Найти координаты точки М(1; 2) в новой системе координат, повернутой относительно старой системы отсчета на угол

Решение:

Воспользуемся полученными формулами 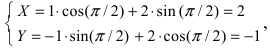т.е. в новой системе координат точка имеет координаты М(2; -1).

Рассмотрим применение преобразования координат:

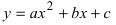
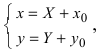
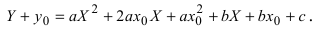
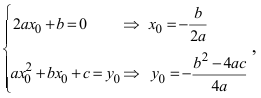
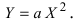
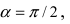
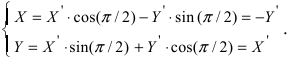
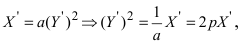
а) Преобразовать уравнение параболы к каноническому виду. Проведем параллельный перенос системы координат получим Выберем начало отсчета новой системы координат так, чтобы выполнялись равенства тогда уравнение принимает вид Выполним поворот системы координат на угол тогда Подставим найденные соотношения в уравнение параболы где параметр параболы

Пример:

Преобразовать уравнение параболы 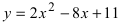к каноническому виду.

Решение:

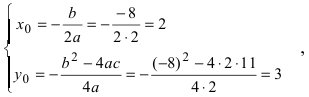
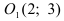
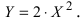
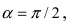
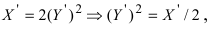
Найдем начало отсчета новой системы координат после параллельного переноса т.е. точка — начало координат новой системы отсчета. В этой системе уравнение параболы имеет вид Проведем поворот системы отсчета на угол тогда

следовательно, параметр параболы р = 1/4.

б) Выяснить, какую кривую описывает функция

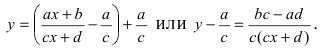
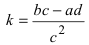
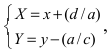
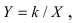
Проведем следующее преобразование Производя параллельный перенос системы координат, вводя обозначение

и новые координаты получим уравнение которое описывает равнобочную гиперболу.

Полярные координаты. Замечательные кривые

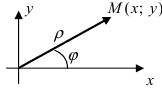
Пусть полярная ось совпадает с осью абсцисс Ох, а начало полярной оси (полюс полярной системы координат) совпадает с началом координат декартовой системы отсчета (Рис. 48). Любая точка М(х;у) в полярной системе координат характеризуется длиной радиус-вектора, соединяющего эту точку с началом отсчета и углом 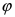между радиус-вектором и полярной осью (угол отсчитывается против часовой стрелки).

Рис. 48. Полярная система координат.

Главными значениями угла 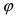являются значения, лежащие в интервале Из рисунка видно, что декартовы и полярные координаты связаны формулами

Рассмотрим замечательные кривые в полярной системе координат:

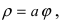
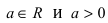
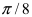
1. Спираль Архимеда где число (Рис. 49). Для построения кривой в полярной системе координат, разобьем декартову плоскость лучами с шагом по углу и на каждом луче отложим ему соответствующее значение р.

Рис. 49. Спираль (улитка) Архимеда.

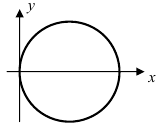
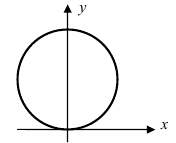
2. Уравнение окружности: уравнение 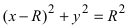описывает окружность с центром в точке A(R; 0) и радиусом R (Рис. 50). В полярной системе координат уравнение принимает вид

Рис. 50. Окружность с центром в точке A(R; 0) и радиусом R.

3. Уравнение 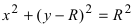описывает окружность с центром в т. А(0; R) и радиусом R (Рис. 51). В полярной системе координат уравнение принимает вид

Рис. 51. Окружность с центром в точке А(0; R) и радиусом R.

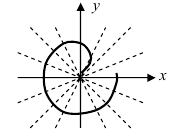
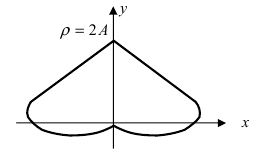
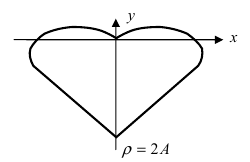
4. Кардиоиды:

Рис. 52. Кардиоида

Рис. 53. Кардиоида

Аналогично выглядят кардиоиды 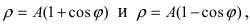но они вытянуты вдоль оси абсцисс Ох.

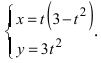
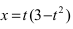
5. Петля: Величина равна нулю при

Для первого корня у = 0, а для второго и третьего — у = 9 . Следовательно, петля имеет вид

Рекомендую подробно изучить предметы:

Математика
Алгебра
Линейная алгебра
Векторная алгебра
Высшая математика
Дискретная математика
Математический анализ
Математическая логика

Ещё лекции с примерами решения и объяснением:

Бесконечно малые и бесконечно большие функции
Замечательные пределы
Непрерывность функций и точки разрыва
Точки разрыва и их классификация
Экстремум функции
Методы решения систем линейных алгебраических уравнений (СЛАУ)
Скалярное произведение и его свойства
Векторное и смешанное произведения векторов

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.