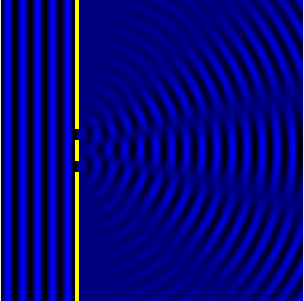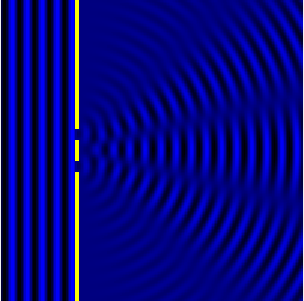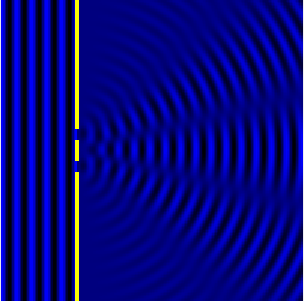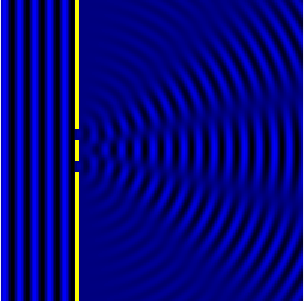
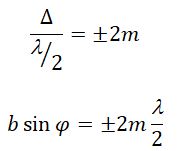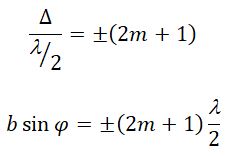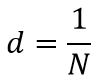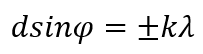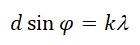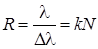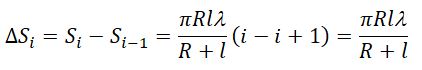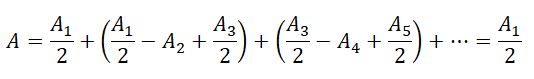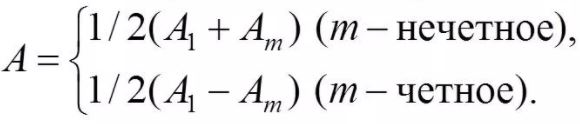Записать и пояснить уравнения максимумов и минимумов при дифракции на дифракционной решетке (4 видео)

Дифракционная решетка. Условия главных максимумов. Дисперсия и разрешающая способность решетки

При анализе действия зонных пластинок мы выяснили, что в дифракции наиболее эффективно работают периодические структуры. И это неудивительно. Ведь дифракция — волновой эффект, а волны и сами представляют собой периодическую структуру. Поэтому можно ожидать, что набор равноудаленных щелей должен в некоторых случаях давать более эффектную и полезную для практических применений дифракционную картину.

В связи с этим рассмотрим точный оптический прибор — дифракционную решетку. Простейшей дифракционной решеткой называют совокупность большого количества узких, параллельных, одинаковых, равноотстоящих друг от друга щелей. Такая решетка работает в проходящем свете. Иногда используют и дифракционную решетку в отраженном свете, которую изготавливают путем нанесения большого количества узких, параллельных, одинаковых, равноотстоящих друг от друга препятствий на зеркало. Часто решетку изготавливают путем нанесения непрозрачных штрихов на прозрачное стекло или зеркало. Поэтому характеризуют ее не количеством щелей, а количеством штрихов, разделяющих щели. Первую работающую дифракционную решетку сделал в XVII в. шотландский ученый Джеймс Грегори, который использовал для этого птичьи перья. У современных решеток число штрихов достигает миллиона на поверхности до нескольких десятков сантиметров.

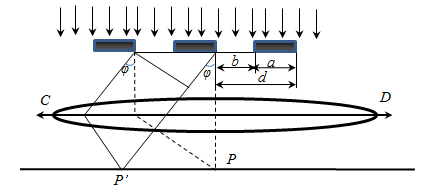
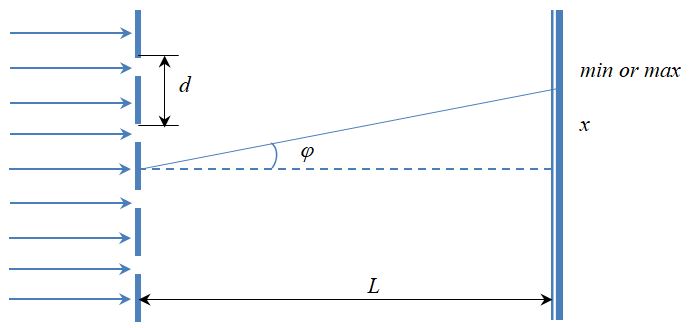
Описание дифракции на дифракционной решетке выполняется подобно описанию дифракции в параллельных лучах на щели (рис. 27.4). Сумму ширины щели а и промежутка между щелями (штриха) Ь называют периодом решетки’.

Пусть на решетку перпендикулярно ее плоскости падает пучок параллельных лучей, который далее в со- Рис. 27.4 ответствии с принципом Гюйгенса — Френеля дает вторичные интерферирующие волны. Выберем некоторое направление прохождения этих вторичных волн, определяемое углом а. Если разность хода волн между серединами соседних щелей равна целому числу волн, то имеет место их взаимное усиление:

Очевидно, что такая же разность хода будет и для левых краев щелей, и для правых краев, и для любых других мар точек, удаленных друг от друга на расстояние d. Более того, если щели не являются соседними и расстояние между их центрами равно не d, а 2d, 3d, id,. то из геометрических соображений очевидно, что разность хода увеличится в целое число раз и останется равной целому числу волн. Это означает многократное взаимное усиление волн от всех щелей решетки и ведет к появлению на экране ярких максимумов, называемых главными. Положение главных максимумов в соответствии с формулой (27.21) задается основной формулой дифракционной решетки:

где т = 0, 1, 2, 3. — порядок главных максимумов. Они расположены симметрично относительно центрального максимума, для которого т = 0.

Кроме главных максимумов существуют дополнительные, когда пучки от одних щелей усиливают друг друга, а от других — гасят. Эти дополнительные максимумы обычно слабые и не представляют интереса.

Перейдем теперь к определению положения минимумов. Очевидно, что в тех направлениях, куда не шел свет от одной щели, туда он не пойдет и от нескольких. Поэтому условие (27.16) определяет положение главных минимумов дифракционной решетки:

При этом если положение главного минимума попадает на положение главного максимума, то главный максимум исчезает.

Однако кроме этих минимумов появятся дополнительные минимумы, обусловленные приходом в противофазе света от разных щелей. Сделаем упрощенную оценку их положения, пренебрегая ролью штрихов. В этом приближении вся решетка представляется единой щелыо, ширина которой равна Nd, где N — число щелей решетки. По аналогии с формулой (27.23) имеем

Сразу ясно, что эта оценка включает в себя позиции более строго вычисленных (с учетом роли штрихов) главных максимумов (27.22). Очевидно, что эти ложные позиции надо исключить. После этого получается достаточно точная формула для определения положения большого количества дополнительных минимумов дифракционной решетки:

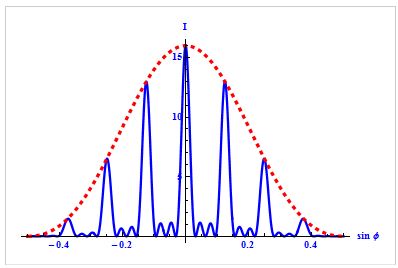
Анализ формулы показывает, что между каждыми двумя главными максимумами имеется N — 1 дополнительных минимумов. При этом чем больше щелей, тем больше минимумов между главными максимумами и тем резче и ярче главные максимумы относительно тусклого фона между максимумами. Если дифракционную решетку осветить двумя пучками света с близкой длиной волны, то решетка с большим числом щелей позволит в дифракционной картине четко разделить и определить эти длины волн. А если осветить решетку белым светом, то каждый главный максимум, кроме центрального, получится разложенным в спектр, называемый дифракционным спектром.

Качество дифракционной решетки как оптического прибора определяется ее угловой дисперсией и разрешающей способностью. Угловая дисперсия D характеризует угловую ширину спектра и показывает, какой интервал углов приходится на единичный интервал длин волн:

Взяв дифференциал от соотношения (27.22), получим

При работе с дифракционной решеткой обычно используют малые углы, так что cos а

1. Поэтому окончательно получаем, что угловая дисперсия (и угловое расстояние между центрами близких спектральных линий) тем больше, чем больше порядок спектра и чем меньше период решетки:

Возможность различать близкие спектральные линии зависит не только от расстояния между центрами линий, но и от ширины линий. Поэтому в оптике вводят еще одну характеристику — разрешающую способность оптического прибора, которая показывает, как хорошо прибор различает мелкие детали предмета. Для дифракционной решетки под разрешающей способностью понимают отношение длины волны к разности близких длин волн, которые решетка еще способна различить:

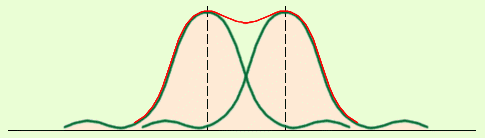
Обычно порог различения линий определяют критерием Рэлея: оптический прибор разрешает две соседние линии спектра, если максимум одной из них попадает в ближайший минимум другой линии (рис. 27.5). В этом случае посередине между интенсивностями центров линий / имеется еще обычно различимый глазом или прибором минимум с интенсивностью

Положение главного максимума первой волны дается уравнением (27.22):

Положение ближайшего добавочного минимума близкой второй волны Х₂ с учетом уравнений (27.22) и (27.25) определяется суммой

На пороге разрешения эти положения (и углы наблюдения) совпадают:

Таким образом, разрешающая способность решетки тем больше, чем больше в ней штрихов и чем больше порядок спектра.

Содержание

Записать и пояснить уравнения максимумов и минимумов при дифракции на дифракционной решетке
Дифракция на щели
Дифракция света
🌟 Видео

Видео:Дифракция света. Дифракционные решетки. 11 класс.Скачать

Записать и пояснить уравнения максимумов и минимумов при дифракции на дифракционной решетке

Дифракция — явление отклонения световых волн от прямолинейного распространения при прохождении света мимо края препятствия. При этом лучи могут попадать в область геометрической тени от препятствия.

Между интерференцией и дифракцией нет существенного физического различия. Оба явления заключаются в перераспределении светового потока в результате наложения (суперпозиции) волн. По историческим причинам отклонение от закона независимости световых пучков, возникающее в результате суперпозиции когерентных волн, принято называть интерференцией волн . Отклонение от закона прямолинейного распространения света, в свою очередь, принято называть дифракцией волн .

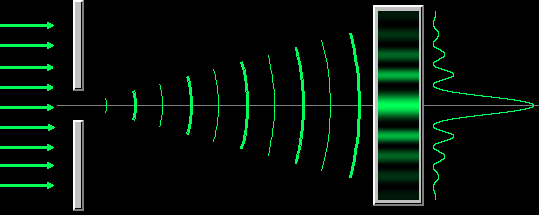
Наблюдение дифракции осуществляется обычно по следующей схеме. На пути световой волны, распространяющейся от некоторого источника, помещается непрозрачная преграда, закрывающая часть волновой поверхности световой волны. За преградой располагается экран, на котором возникает дифракционная картина.

Различают два вида дифракции. Если источник света S и точка наблюдения P расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку P, образуют практически параллельные пучки, говорят о дифракции в параллельных лучах или о дифракции Фраунгофера . В противном случае говорят о дифракции Френеля . Количественный критерий, позволяющий установить, какой вид дифракции имеет место, определяется величиной безразмерного параметра b 2 /lλ, где b – характерный размер препятствия, l – расстояние между препятствием и экраном, на котором наблюдается дифракционная картина, λ – длина волны.

Свойства дифракции:

1) Дифракция волн – характерная особенность распространения волн независимо от их природы.

2) Волны могут попадать в область геометрической тени (огибать препятствия, проникать через небольшие отверстия в экранах). Например, звук хорошо слышен за углом дома — звуковая волна его огибает. Дифракцией радиоволн вокруг поверхности Земли объясняется прием радиосигналов в диапазоне длинных и средних радиоволн за пределами прямой видимости излучающей антенны.

3) Дифракция волн зависит от соотношения между длиной волны и размером объекта, вызывающего дифракцию. В пределе при λ→0 законы волновой оптики переходят в законы геометрической оптики. Дифракция обнаруживается в тех случаях, когда размеры огибаемых препятствий соизмеримы с длиной волны.

Объяснить явление дифракции можно исходя из принципа Гюйгенса-Френеля .Этот принцип представляет собой правило, объясняющее, как, исходя из положения волнового фронта в данный момент, найти новое положение волнового фронта в последующий момент времени.

Гюйгенс предложил рассматривать каждую точку среды, которой достигла волна, как источник вторичных сферических волн, распространяющихся по всем направлениям со скоростью, присущей данной среде . Поверхность, огибающая вторичные волны, представляет собой фронт волны в данный момент времени.

Френель дополнил изложенный принцип следующим положением: вторичные сферические волны являются когерентными и колебания в любой точке пространства, которой вторичные волны достигнут в момент времени t, представляют собой результат интерференции этих вторичных волн .

Принцип Гюйгенса — Френеля формулируется следующим образом:

Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Дифракция Фраунгофера от одной щели

Дифракция Фраунгофера наблюдается, когда источник света сильно удален от места наблюдения, в результате фронт волны можно считать плоским.

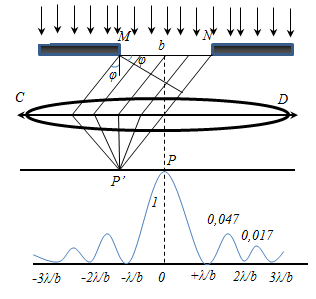
Разность хода двух волн от краев щели равна Δ = b sin φ .

Разобьем MN на отрезки длиной λ/2. Параллельно произвольному направлению луча через точки разбиения (1, 2, 3) проведем линии, которые разделят открытую часть волновой поверхности MN на участки равной ширины – зоны Френеля, параллельные краям щели. По построению ∆ – разность хода лучей от краев зон Френеля равна λ/2. Это означает, что волны, идущие от двух соседних зон при наложении погасят друг друга. Т.о., если на открытой части волновой поверхности для данного направления наблюдения уложится целое четное число зон Френеля, то для данного направления будет наблюдаться min интенсивности, т.к. зоны попарно друг друга погасят.

Четное число зон Френеля — минимум дифракции

Если число зон Френеля целое и нечетное, то в этом направлении будет наблюдаться max:

Дифракционная решетка

Совокупность большого числа щелей и промежутков между ними называется дифракционной решеткой.

а — ширина промежутка между щелями;

N — число щелей, приходящихся на единицу длины

Дифракционная картина на решетке определяется как интерференция волн, приходящих от всех щелей, т. е. дифракция на решетке — многолучевая интерференция. Поскольку щели разделены одинаковым расстоянием, разности хода лучей, поступающих из двух соседних щелей, будут для направления φ идентичны по всей решетке.

В областях, в которых существует минимум при одной щели, минимумы будут и в случае N щелей, т. е. условие первичного минимума дифракционной решетки аналогично условию минимума для одной щели:

— условие главных минимумов.

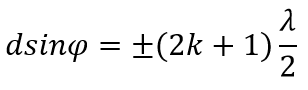
Условие главных максимумов :

Эти максимумы расположены симметрично относительно центра (k = 0) и главного максимума.

Между основными пиками есть дополнительные очень слабые пики, интенсивность которых значительно меньше, чем у основных пиков (1/22 интенсивности ближайшего главного максимума). Количество дополнительных максимумов равно N — 2, где N — количество штрихов решетки.

Между главными максимумами будут расположены (N-1) дополнительных минимумов.

Разрешающая способность дифракционной решетки

Размер дифракционных изображений очень мал. Например, радиус центрального светлого пятна в фокальной плоскости линзы диаметром D = 5 см с фокусным расстоянием F = 50 см в монохроматическом свете с длиной волны λ = 500 нм приблизительно равен 0,006 мм. Но в высокоточных астрономических приборах реализуется дифракционный предел качества изображений. Вследствие дифракционного размытия изображения двух близких точек объекта могут оказаться неотличимыми от изображения одной точки.

Спектральной разрешающей способностью R решетки, характеризующей возможность разделения с ее помощью двух близких спектральных линий с длинами волн λ и λ + Δλ, называется отношение длины волны λ к минимально возможному значению Δλ

Пусть решетка имеет период d = 10 –3 мм, ее длина L = 10 см. Тогда, N = 10 5 (это хорошая решетка). В спектре 2-го порядка разрешающая способность решетки оказывается равной R = 2·10 5 . Это означает, что минимально разрешимый интервал длин волн в зеленой области спектра (λ = 550 нм) равен Δλ = λ / R ≈ 2,8·10 –3 нм.

Действие оптических приборов описывается законами геометрической оптики. Согласно этим законам можно различать с помощью микроскопа сколь угодно малые детали объекта; с помощью телескопа можно установить существование двух звезд при любых малых угловых расстояниях между ними. Однако в действительности это не так, и лишь волновая теория света позволяет разобраться в причинах предела разрешающей способности оптических приборов.

Метод зон Френеля

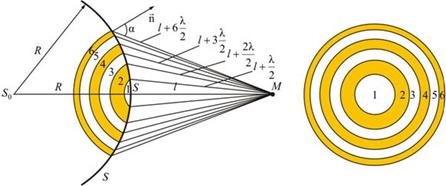
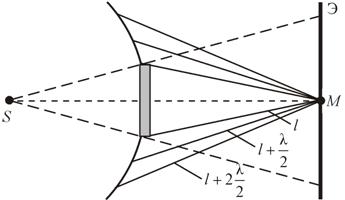
Границей первой (центральной) зоны служат точки поверхности S, находящиеся на расстоянии l + λ/2 от точки M. Точки сферы S, находящиеся на расстояниях l + 2λ/2, l + 3λ/2 , и т.д. от точки M , образуют 2, 3 и т.д. зоны Френеля.

Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M Δ = λ/2.

Поэтому при сложении этих колебаний, они должны взаимно ослаблять друг друга: A = A₁ + A₂ + A₃ +. + A_i.

где A – амплитуда результирующего колебания, A_i – амплитуда колебаний, возбуждаемая i-й зоной Френеля.

Величина A_i зависит от площади S_i зоны и угла α_i между нормалью к поверхности и прямой, направленной в точку M.

Площадь одной зоны

Отсюда видно, что площадь зоны Френеля не зависит от номера зоны i. Это значит, что при не слишком больших i площади соседних зон одинаковы.

В то же время с увеличением номера зоны возрастает угол α_i и, следовательно, уменьшается интенсивность излучения зоны в направлении точки M, т.е. уменьшается амплитуда A_i. Она уменьшается также из-за увеличения расстояния до точки M .

Отсюда следует, что углы между нормалью к зоне и направлением на точку M у соседних зон примерно равны, т.е. что амплитуды волн, приходящих в точку M от соседних зон, примерно равны.

Приближенно можно считать, что амплитуда колебания A m от некоторой m -й зоны равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е.

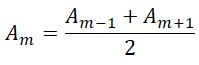
Тогда выражение для амплитуды можно записать в виде

Так как площади соседних зон одинаковы, то выражения в скобках равны нулю, значит результирующая амплитуда А = A₁ /2.

Интенсивность излучения J

Таким образом, результирующая амплитуда, создаваемая в некоторой точке M всей сферической поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной, а интенсивность J = J₁/4 .

Так как радиус центральной зоны мал ( r₁ = 0,16 мм), следовательно, можно считать, что свет от точки P до точки M распространяется прямолинейно.

Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только центральную зону Френеля, то амплитуда в точке M будет равна A₁. Соответственно, интенсивность в точке M будет в 4 раза больше, чем при отсутствии экрана (т.к. J = 4J₁ ). Интенсивность света увеличивается, если закрыть все четные зоны.

Таким образом, принцип Гюйгенса–Френеля позволяет объяснить прямолинейное распространение света в однородной среде.

Дифракция на простых объектах

Дифракция на щели

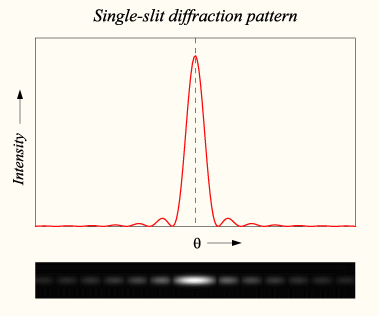
Дифракция от круглого отверстия
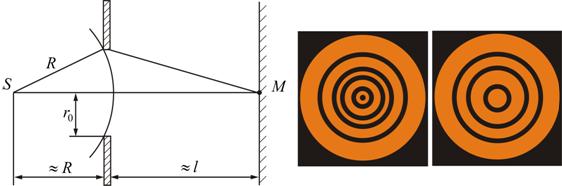
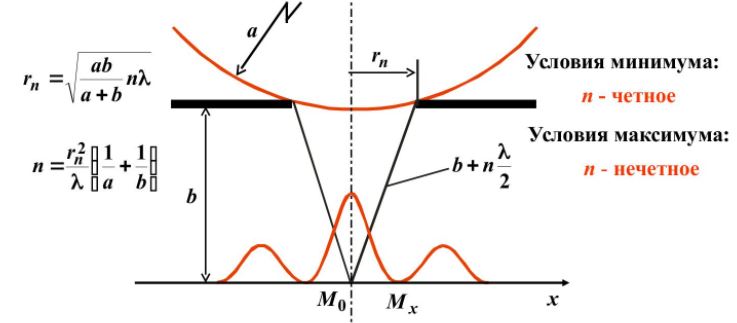
Поставим на пути сферической световой волны непрозрачный экран с круглым отверстием радиуса . Экран расположен так, что перпендикуляр, опущенный из S на непрозрачный экран, попадает точно в центр отверстия.

Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. К огда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке М будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю.

Дифракция на круглом отверстии при открытом чётном (слева) и не чётном (справа) числе зон.

Естественно, что если r₀>>λ, то никакой дифракционной картины не будет.

Дифракция от диска
Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск.

В центре тени светлое пятно

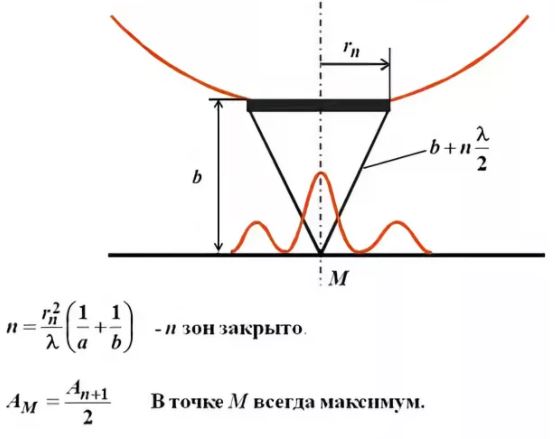
Амплитуда световых колебаний в точке M равна половине амплитуды, обусловленной первой открытой зоной. Если размер диска невелик (охватывает небольшое число зон), то действие первой зоны немногим отличается от действия центральной зоны волнового фронта. Таким образом, освещенность в точке M будет такой же, как и в отсутствие экрана. Вследствие симметрии центральная светлая точка будет окружена кольцами света и тени (вне границ геометрической тени).

Парадоксальное, на первый взгляд, заключение, в силу которого в самом центре геометрической тени может находиться светлая точка, было выдвинуто Пуассоном в 1818 г. и впоследствии было названо его именем. «Пятно Пуассона» подтверждает правильность теории Френеля.

Видео:Урок 420. Дифракция света. Дифракционная решеткаСкачать

Дифракция света

В рамках геометрической оптики, распространение луча в оптически однородной среде — прямолинейное, однако в природе существует ряд явлений, где можно наблюдать отклонение от этого условия.

Дифракция – явление огибания световыми волнами встреченных препятствий. В школьной физике изучаются две дифракционные системы (системы, при прохождении луча в которых наблюдается дифракция):

дифракция на щели (прямоугольном отверстии)
дифракция на решётке (набор равноотстоящих друг от друга щелей)

Дифракция на щели — дифракция на прямоугольном отверстии (рис. 1).

Рис. 1. Дифракция на щели

Пусть дана плоскость со щелью, шириной , на которую под прямым углом падает пучок света А. Большинство света проходит на экран, однако часть лучей дифрагирует на краях щели (т.е. отклоняется от своего первоначального направления). Далее эти лучи интерферируют друг с другом с образованием дифракционной картины на экране (чередование ярких и тёмных областей). Рассмотрение законов интерференции достаточно сложно, поэтому ограничимся основными выводами.

Полученная дифракционная картина на экране состоит из чередующихся областей с дифракционными максимумами (максимально светлыми областями) и дифракционными минимумами (максимально тёмными областями). Эта картина симметрична относительно центрального светового пучка. Положение максимумов и минимумов описывается углом относительно вертикали, под которым они видны, и зависит от размера щели и длины волны падающего излучения. Положение этих областей можно найти используя ряд соотношений:

для дифракционных максимумов

где
— ширина щели,
— угол между вертикалью и направлением на максимум,
— порядок максимума (счётчик),
— длина волны света.

Нулевым максимумом дифракции называется центральная точка на экране под щелью (рис. 1).

для дифракционных минимумов

где
— ширина щели,
— угол между вертикалью и направлением на минимум,
— порядок минимума (счётчик),
— длина волны света.

Вывод: по условиям задачи необходимо выяснить: максимум или минимум дифракции необходимо найти и использовать соответствующее соотношение (1) или (2).

Дифракция на дифракционной решётке.

Дифракционной решёткой называется система, состоящая из чередующихся щелей, равноотстоящих друг от друга (рис. 2).

Рис. 2. Дифракционная решётка (лучи)

Так же, как и для щели, на экране после дифракционной решётки будет наблюдаться дифракционная картина: чередование светлых и тёмных областей. Вся картина есть результат интерференции световых лучей друг с другом, однако на картину от одной щели будет воздействовать лучи от других щелей. Тогда дифракционная картина должна зависеть от количества щелей, их размеров и близкорасположенности.

Введём новое понятие — постоянная дифракционной решётки:

где
— постоянная дифракционной решётки,
— расстояние между щелями,
— ширина щели.

Тогда положения максимумов и минимумов дифракции:

для главных дифракционных максимумов (рис. 3)

где
— постоянная дифракционной решётки,
— угол между вертикалью и направлением на максимум.
— порядок максимума (счётчик),

Рис. 3. Дифракционная решётка (максимумы)

для дифракционных минимумов

где
— ширина щели,
— угол между вертикалью и направлением на минимум,
— порядок минимума (счётчик),
— длина волны света.

Отдельным вопросом задач на дифракцию является вопрос о наибольшем количестве максимумов, которые можно наблюдать в текущей системе. Наибольший угол, под которым можно наблюдать максимум — , тогда, исходя из (4):

Главное помнить, что число максимумов — число, т.е. от полученного ответа необходимо брать только целую часть.

Вывод: по условиям задачи необходимо выяснить: максимум или минимум дифракции необходимо найти и использовать соответствующее соотношение (4) или (5).

Общий вывод: задачи на дифракцию должны содержать в себе словосочетания, связанные с «дифракцией». Далее разбираемся с объектом: щель или дифракционная решётка и используем соответствующие соотношения для минимума или максимума.