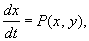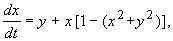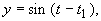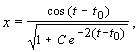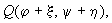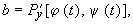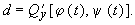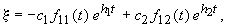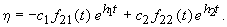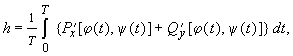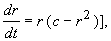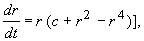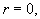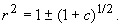Система обыкновенных дифференциальных уравнений называется автономной, если независимая переменная не входит явно в систему.
Рассмотрим автономные системы второго порядка: 
Будем полагать, что правые части системы f1(x1, x2), f2(x1, x2) непрерывно дифференцируемы в области определения, т.е. справедлива теорема существования и единственности.
Название автономная система оправдано тем, что решение само управляет своим изменением, поскольку производные dx1/dt и dx2/dt зависят только от x1 и x2. Автономные системы называют также динамическими системами.
Пусть x1= j 1(t), x2= j 2(t) — решение автономной системы второго порядка. Тогда уравнения 
задают в параметрической форме кривую на плоскости (x1, x2). Эта кривая называется фазовой кривой или фазовой траекторией системы. Плоскость, на которой расположены фазовые траектории называется фазовой плоскостью автономной системы. Именно поэтому автономные системы второго порядка принято называть автономными системами на плоскости.
Для фазовых траекторий автономной системы с непрерывно дифференцируемой правой частью справедливы следующие утверждения:
- две фазовые кривые либо не имеют общих точек, либо совпадают;
- фазовая траектория, отличная от точки, есть гладкая кривая (в каждой ее точке есть ненулевой касательный вектор);
- всякая фазовая кривая принадлежит к одному из трех типов— гладкая кривая без самопересечений, замкнутая гладкая кривая (цикл), точка.
ПРИМЕР 1. Виды фазовых кривых.
Если фазовая траектория x1= j1(t), x2= j2(t) — замкнутая гладкая кривая g, в некоторой окрестности которой нет других замкнутых траекторий, то она является предельным циклом: все траектории, которые начинаются достаточно близко от g, спиралевидно приближаются к ней либо при 

Предельные циклы бывают трех типов:
- устойчивые — близкие траектории «навиваются» на него при
(пример 2);
- неустойчивые— близкие траектории уходят от него при
(пример 3);
- полуустойчивые — траектории, лежащие по одну сторону от цикла, «навиваются» на него при
, а лежащие по другую строну — «отходят» от цикла (пример 4).
ПРИМЕР 2. Устойчивый предельный цикл.
ПРИМЕР 3. Неустойчивый предельный цикл.
ПРИМЕР 4. Полуустойчивый предельный цикл.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Замкнутые траектории предельные циклы дифференциальные уравнения
КОЛЕБАНИЯ В БИОЛОГИЧЕСКИХ СИСТЕМАХ
Понятие автоколебаний. Изображение автоколебательной системы на фазовой плоскости. Предельные циклы. Условия существования предельных циклов. Рождение предельного цикла. Бифуркация Андронова ‑ Хопфа. Мягкое и жесткое возбуждение колебаний. Модель брюсселятор. Примеры автоколебательных моделей процессов в живых системах. Колебания в темновых процессах фотосинтеза. Автоколебания в модели гликолиза. Внутриклеточные колебания концентрации кальция. Клеточные циклы.
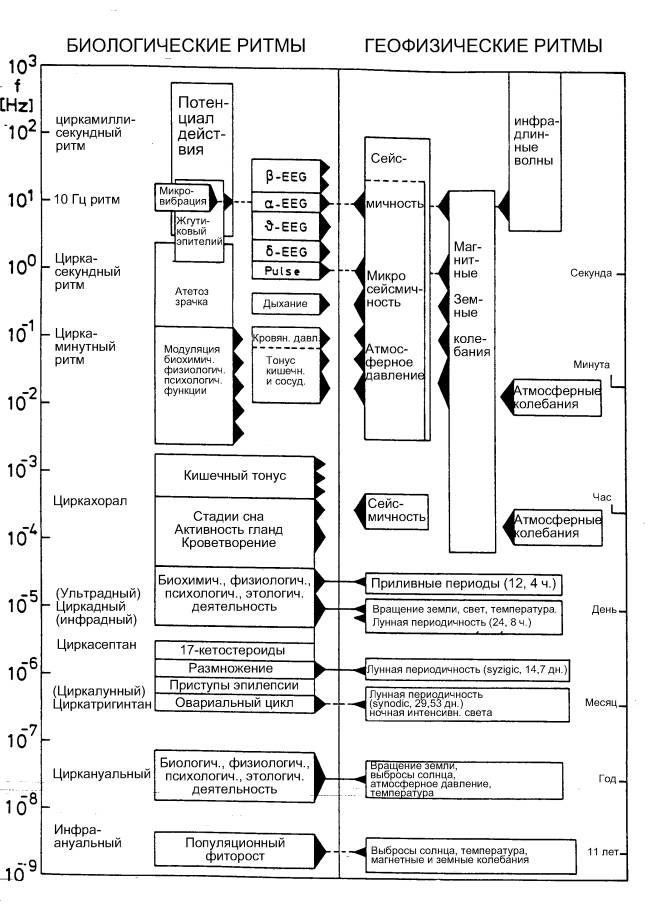
Для биологических систем характерно периодическое изменение различных характеристик. Период этих колебаний может быть связан с периодическими изменениями условий жизни на Земле — смена времен года, смена дня и ночи. Существуют и другие геофизические ритмы –солнечные, лунные, связанные с периодами атмосферных явлений. Геофизические и биологические ритмы сопоставлены на рис. 8.1. Но многие периодические процессы имеют частоту изменения, не связанную очевидным образом с внешними геокосмическими циклами. Это так называемые «биологические часы» различной природы, начиная от колебаний биомакромолекул, биохимических колебаний, вплоть до популяционных волн.
Внутриклеточные колебания задают эндогенные биологические ритмы, которые свойственны всем живым системам. Именно они определяют периодичность деления клеток, отмеряют время рождения и смерти живых организмов. Модели колебательных систем используются в ферментативном катализе, теории иммунитета, в теории трансмембранного ионного переноса, микробиологии и биотехнологии.
С некоторыми из типов периодических движений мы уже имели дело при рассмотрении особых точек типа центр и затухающих или нарастающих колебаний в случае устойчивого и неустойчивого фокуса. Однако «биологические часы» имеют свойство, отличающее их от рассмотренных типов колебаний — неизменность во времени периода и амплитуды таких колебаний, означающую стационарность и устойчивость колебательного режима.
Рис. 8.1. Космофизические, геофизические и биологические ритмы. Справа – шкала периодов, слева – шкала частот
В данном случае периодическое изменение величин представляет собой один из типов стационарного поведения системы. Если колебания в системе имеют постоянные период и амплитуду, устанавливаются независимо от начальных условий и поддерживаются благодаря свойствам самой системы, а не вследствие воздействия периодической силы, система называется автоколебательной.
Видео:Сергеев И. Н. - Дифференциальные уравнения II - Циклы в фазовых пространствахСкачать

Незатухающие колебания в таких системах устойчивы, так как отклонения от стационарного колебательного режима затухают. К классу автоколебательных систем относятся колебания в гликолизе и других метаболических системах, периодические процессы фотосинтеза, колебания концентрации кальция в клетке, колебания численности животных в популяциях и сообществах.
Предельный цикл. В фазовом пространстве такому типу поведения соответствует притягивающее множество (аттрактор), называемое предельным циклом .
Предельный цикл есть изолированная замкнутая кривая на фазовой плоскости, к которой в пределе при t ® ¥ стремятся все интегральные кривые . Предельный цикл представляет стационарный режим с определенной амплитудой, не зависящий от начальных условий, а определяющийся только организацией системы. Существование предельного цикла на фазовой плоскости есть основной признак автоколебательной системы. Очевидно, что при автоколебательном процессе фаза колебаний может быть любой.
Остановимся на общих характеристиках автоколебательных систем. Рассмотрим систему уравнений общего вида:
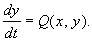
Если T (T > 0) — наименьшее число, для которого при всяком t
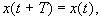
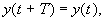
то изменение переменных x = x ( t ), y = y ( t ) называется периодическим изменением с периодом T .
Периодическому изменению соответствует замкнутая траектория на фазовой плоскости, и обратно: всякой замкнутой траектории соответствует бесконечное множество периодических изменений, отличающихся друг от друга выбором начала отсчета времени.
Если периодическому изменению на фазовой плоскости соответствует изолированная замкнутая кривая, к которой с внешней и внутренней стороны приближаются (при возрастании t) соседние траектории по спиралям, эта изолированная замкнутая траектория есть предельный цикл.
Простые примеры позволяют убедиться, что система общего вида (8.1) допускает в качестве траекторий предельные циклы.
Например, для системы
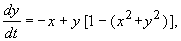
траектория 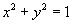
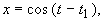
а уравнения всех других фазовых траекторий запишутся в виде:
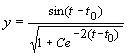
Значениям постоянной интегрирования С > 0 соответствуют фазовые траектории, накручивающиеся на предельный цикл изнутри (при t ® ¥ ), а значениям –1 C 0 траектории, накручивающиеся снаружи.
Предельный цикл называется устойчивым, если существует такая область на фазовой плоскости, содержащая этот предельный цикл, — окрестность e , что все фазовые траектории, начинающиеся в окрестности e , асимптотически при t ® ¥ приближаются к предельному циклу.
Если же, наоборот, в любой сколь угодно малой окрестности e предельного цикла существует по крайней мере одна фазовая траектория, не приближающаяся к предельному циклу при t ® ¥ , то такой предельный цикл называется неустойчивым . Такие циклы разделяют области влияния (бассейны) разных притягивающих множеств.
На рис. 8.2 изображены устойчивый предельный цикл ( а) и неустойчивые ( б) и ( в).
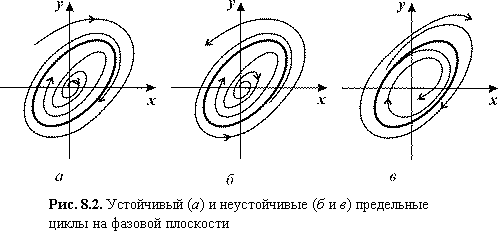 |
Неустойчивые предельные циклы, подобные изображенному на рис. 8.2 б, такие, что все траектории с одной стороны (например, изнутри) приближаются к ним, а с другой стороны (например, извне) удаляются от них при t ® ¥ , называют «полуустойчивыми» или двойными. Последнее название связано с тем, что обычно такие циклы при подходящем изменении параметра системы расщепляются на два, один из которых устойчив, а другой неустойчив.
А.М. Ляпунов показал, что для исследования устойчивости периодического движения x = j ( t), y = y ( t) можно идти по пути линеаризации уравнений, подобно тому, как мы это делали при исследовании устойчивости состояний равновесия. Если положить
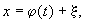
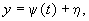
подставить эти выражения в уравнения (8.1), разложить правые части этих уравнений — функции
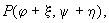
в ряды по степеням x и h и отбросить нелинейные члены, то мы получим линейные уравнения (уравнения первого приближения) для координат возмущения x и h :
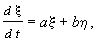
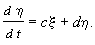
Коэффициенты в правой части:
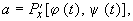
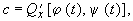
Видео:Лекция 2.12 Предельные циклы на плоскости. Диффуры – И.В. АсташоваСкачать

Это система линейных дифференциальных уравнений с периодическими коэффициентами периода T, поскольку a, b, c, d суть функции от j , y — периодических функций времени с периодом T. Общий вид ее решения
Здесь 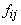
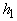
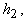
где x = j ( t ), y = y ( t ) — любое периодическое решение, соответствующее рассматриваемому предельному циклу, T — период решения.
Таким образом, устойчивость предельного цикла (и устойчивость в смысле Ляпунова соответствующих периодических движений) определяется знаком характеристического показателя. Предельный цикл устойчив, если h 0 и неустойчив, если h > 0. Если же h = 0, уравнения первого приближения не решают вопроса об устойчивости периодического движения.
Для нахождения предельных циклов не существует таких простых аналитических методов, как для нахождения стационарных точек и исследования их устойчивости. Однако, исследование фазовой плоскости системы позволяет ответить на вопрос, есть в данной системе предельный цикл, или нет.
Сформулируем несколько теорем, определяющих наличие предельного цикла по топологическому строению фазовой плоскости. Они могут быть полезны как при аналитическом, так и при компьютерном анализе системы.
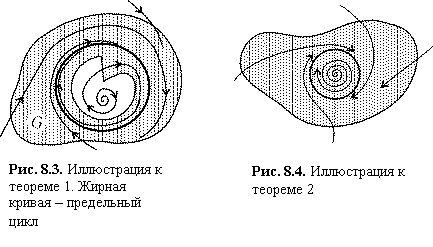
Теорем а 1. Пусть на фазовой плоскости существует область, из которой фазовые траектории не выходят, и в которой нет положений равновесия (особых точек). Тогда в этой области обязательно существует предельный цикл, причем все остальные траектории обязательно наматываются на него.
На рис. 8.3. изображена такая область G, из которой фазовые траектории не выходят. Это означает, что фазовые траектории либо входят, пересекая границу, внутрь области, либо сама граница является траекторией. Легко видеть, что такая область не может быть односвязной. Поскольку траектория наматывается на предельный цикл изнутри, это означает, что внутри этого предельного цикла на фазовой плоскости существует либо неустойчивая особая точка, либо неустойчивый предельный цикл, очевидно, не принадлежащие рассматриваемой области G.
Таким образом, если найти на фазовой плоскости такую двусвязную область, что направления фазовых траекторий на всей границе обращены внутрь этой области, то можно утверждать, что внутри этой области имеется предельный цикл.
Теорема 2. Если существует на фазовой плоскости некоторая замкнутая область, такая, что все фазовые траектории, пересекающие границу этой области, входят в нее, и внутри этой области находится неустойчивая особая точка, то в этой области обязательно имеется хотя бы один предельный цикл (рис. 8.4)
Рис. 8.4. Иллюстрация к теореме 2
Рис. 8.3. Иллюстрация к теореме 1. Жирная кривая – предельный цикл
 |
Приведем также некоторые критерии отсутствия замкнутых фазовых траекторий (в том числе предельных циклов).
1. Если в системе не существует особых точек, то в ней не может быть и замкнутых фазовых траекторий.
2. Если в системе существует только одна особая точка, отличная от узла, фокуса и центра (например, седло), то такая система не допускает замкнутых фазовых траекторий.
3. Если в системе имеются только простые особые точки, причем через все точки типа узел и фокус проходят интегральные кривые, уходящие на бесконечность, то в такой системе нет замкнутых фазовых траекторий.
В случае, если критерии 1–3 выполнены, можно с уверенностью утверждать, что в системе нет предельных циклов. Однако невыполнение этих критериев еще не позволяет сделать вывод о наличии в системе предельных циклов и, следовательно, автоколебаний.
Рис. 8.5. Фазовый портрет системы, имеющий устойчивый и неустойчивый (пунктир) предельные циклы
 |
Неустойчивый предельный цикл также может содержаться в фазовом портрете грубых систем. Однако такой предельный цикл не соответствует реальному периодическому процессу, он играет лишь роль «водораздела», по обе стороны которого траектории имеют различное поведение. Например, на рис. 8.5 представляет собой сепаратрису, отделяющую область тяготения траекторий к устойчивой особой точке, с одной стороны, и к устойчивому предельному циклу, с другой.
Рождение предельного цикла. Бифуркация Андронова-Хопфа.
Существование предельных циклов возможно лишь в системе типа (8.1), правые части которой представлены нелинейными функциями.
На бифуркационной диаграмме 4.11 мы видели, что при пересечении оси абсцисс происходит смена устойчивости фокуса. Нулевым значениям действительной части характеристических чисел (ляпуновских показателей) соответствует особая точка типа центр. В нелинейной системе, где возникает неустойчивый фокус, при этом возможно рождение предельного цикла. Такой переход легко проследить в «модельной» системе:
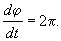
Видео:Дифференциальные уравнения 6. Фазовые траектории. Особые точки автономных системСкачать

Схематически возникновение предельного цикла в системе (8.3) изображено на фазопараметрической диаграмме на рис. 8.6.
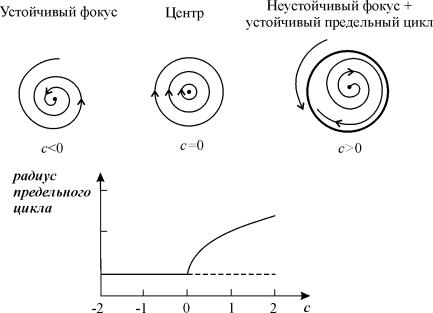
Рис. 8.6. Закритическая (суперкритическая) бифуркация Андронова-Хопфа. Мягкое возбуждение. При с>0 возникают автоколебания, амплитуда которых растет с увеличением с.
Выполнению условия Re l 1,2 = 0, причем Im l 1,2 ¹ 0, соответствует бифуркация Андронова–Хопфа или бифуркация рождения (исчезновения) предельного цикла. Бифуркация впервые была исследована А.А. Андроновым для случая N = 2 и обобщена Е. Хопфом на системы с произвольной размерностью. (Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М., Наука, 1981; Hopf E ., 1942)
Существуют два типа бифуркации Андронова–Хопфа. Только что мы рассмотрели суперкритическую бифуркацию (мягкое возбуждение автоколебаний). Возможна также субкритическая бифуркация (жесткое возбуждение автоколебаний). В этом случае при бифуркационном значении параметра устойчивый фокус теряет устойчивость из-за «влипания» в него неустойчивого предельного цикла (рис. 8.7). Фокус становится неустойчивым, а аттрактором при этом может стать предельный цикл большой амплитуды.
Рис. 8.7. Докритическая (субкритическая) бифуркация Андронова – Хопфа. Жесткое возбуждение автоколебаний. «Локальные события» при изменении параметра при переходе через бифуркационное значение: устойчивый фокус и неустойчивый предельный цикл пунктир, ( а) при уменьшении параметра с переходят в центр (б) , а затем в неустойчивый фокус ( в). Внешний большой устойчивый предельный цикл находится за пределами локальной системы, в которой происходит бифуркация.
 |
«Модельной» системой (см. лекция 6), описывающей рождение предельного цикла при жестком возбуждении, является система:
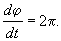
Приравняв правую часть первого уравнения нулю, получим стационарные значения r :
Ветвь r = 0 устойчива при c c > 0.
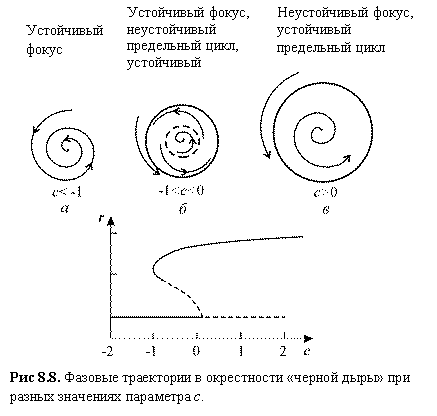
Рис 8.8. Фазовые траектории в окрестности «черной дыры» при разных значениях параметра c .
устойчивый предельный цикл
 |
При с > –1 стационарное решение 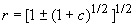
При –1 с 0 стационарное решение 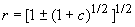
Рассмотрим, что произойдет, если двигаться по параметру с, начиная с отрицательных значений (Рис.8.8). Первоначально имеется единственное устойчивое стационарное состояние r = 0, колебаний нет. При c > –1 существует также устойчивый предельный цикл, но система не покидает своего устойчивого стационарного состояния. Однако после того как с становится положительным, стационарное состояние становится неустойчивым, и происходит резкий скачок к устойчивому предельному циклу. В системе начинаются колебания сразу большой амплитуды. Если двигаться от положительных значений с к отрицательным, колебания большой амплитуды сохраняются до тех пор, пока с не станет меньше –1, а затем внезапно исчезнут. Таким образом при –1 с 0 могут существовать два различных типа поведения. Какой из них реализуется, зависит от предыстории системы. Такой феномен называется эффектом гистерезиса.
При увеличении параметра с и его переходе через ноль скачком возникают устойчивые автоколебания конечной амплитуды и частоты. Для промежуточных значений параметра с существуют два типа устойчивого поведения (два аттрактора) — устойчивое стационарное состояние и устойчивый предельный цикл.
Винфри ( Winfree A . T . ) назвал области, в которых возможны два режима: устойчивая точка покоя и предельный цикл, — черной дырой (рис. 8.8 б) . В этой области параметров можно так приложить возмущение к колебательной системе, что она попадет в область притяжения точки покоя, что приведет к прекращению колебаний. В частности, это показано для уравнений Ходжкина–Хаксли, моделирующих проведение нервного импульса (см. ниже).
Брюсселятор. Простейшим классическим примером существования автоколебаний в системе химических реакций является тримолекулярная модель «Брюсселятор», предложенная в Брюсселе Пригожиным и Лефевром (1965). Основной целью при изучении этой модели было установление качественных типов поведения, совместимых с фундаментальными законами химической и биологической кинетики.
В этом смысле блюсселятор играет роль базовой модели, такую же как гармонический осциллятор в физике, или модели Вольтерра в динамике популяций. Во 2-й части лекций мы остановимся на пространственно‑временных свойствах распределенной системы, локальным элементом которой является брюсселятор. Здесь мы рассмотрим свойства брюсселятора как автоколебательной системы.
Брюсселятор содержит простейшую реализацию кубической нелинейности посредством химической реакции
Хотя тримолекулярная стадия в химической кинетике не столь распространена, как бимолекулярные процессы, выражения для скорости ряда биохимических реакций в определенных случаях можно свести к кубическому виду. В качестве примера приведем следующую последовательность ферментативных реакций:
Здесь предполагается что фермент E имеет по крайней мере три каталитических центра, способных одновременно фиксировать две молекулы X и одну молекулу Y . Если образующиеся комплексы распадаются с достаточно большой скоростью, а ферменты присутствуют в небольших количествах, легко показать, что всю последовательность реакций можно свести к одной стадии, дающей нелинейный член типа X 2 Y в выражении для скорости реакции.
Брюсселятор представляет собой следующую схему гипотетических химических реакций:
🔍 Видео
18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Предельные циклы и автоколебания 1Скачать

Дифференциальные уравнения 9. Предельные множества. Предельные циклыСкачать

11. Уравнения в полных дифференциалахСкачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Лекция 12Скачать

Дифференциальные уравнения. 11 класс.Скачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Поле направлений дифференциального уравнения первого порядкаСкачать

Дифференциальные уравнения 10. Отображение Пуанкаре. Линейные уравнения с частными производнымиСкачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Уравнения с частными производными 1 порядкаСкачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Фазовый портретСкачать