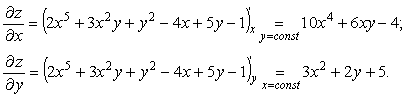Рассмотрим в двухмерной области Q с R’ уравнение с частными
производными второго порядка (9.4):
где мы воспользовались сокращенной формой записи частных производных
Будем считать, что коэффициенты я. уравнения (9.7) достаточно гладкие действительные функции, например afj е С 2 (?2). Будем также предполагать, что ди ^ 0 в области ?2.
Поставим задачу об упрощении уравнения (9.7). Одним из способов упрощения уравнений является замена независимых переменных. Перейдем в уравнении (9.7) от независимых переменных х, у к новым независимым переменным ?, 77 с помощью невырожденного преобразования
где (р,ц/ еС 2 (?2) — заданные действительные функции.
Преобразование (9.8) называется невырожденным в области ?2. если определитель (якобиан), составленный из частных производных первого порядка,
в любой точке (х ,у)е?2. Из условия (9.9) следует, что
gratis *0, grad^^O в любой точке области ?2. Напомним, что по опрсде-
лению, grdacp-— i Н—у, где f и у — единичные орты, направленные
по осям х и у в декартовой системе координат.
Запишем дифференциальное уравнение (9.7) в новых переменных ?, 77, вычисляя производные, входящие в данное уравнение, по правилу дифференцирования сложной функции двух переменных
Подставив найденные выражения в (9.7), получим уравнение с частными производными в новых переменных:
где новые коэффициенты уравнения рассматриваются как функции переменных I] и определяются формулами
У тверждение 9.1. При невырожденном действительном преобразовании (9.8) тип уравнения (9.7) сохраняется.
Доказательство. Определим тип уравнения (9.13), вычислив дискриминант с учетом формул (9.14). После вычислений получим

Таким образом, знак дискриминанта D уравнения (9.7) совпадает со знаком дискриминанта D уравнения (9.13).
Поставим задачу о нахождении функций , _У) уравнения (9.18) и взять в качестве новых переменных % = (р(х,у) и T] = i//(x,у). В этом случае коэффициенты аи =0 и й,2 = 0, что упростит вид уравнения (9.13).
Напомним (см. определение 1.6), что функция #>(дг,у), где ере С’ (О). grad
в области ?2, если на любом решении у= y(.v) этого уравнения функция (р <х,у) постоянна, т.с. имеет место равенство
причем постоянные С могут различаться для разных решений уравнения (9.19). Первым интегралом также называют само соотношение 0 в области ?2. Тогда функция г = ??(*, >’) удовлетворяет уравнению с частными производными (9.18) в области ?2.
Доказательство. Зафиксируем точку М0 =(*0,>’0)е?2 и построим решение у=у(х) соответствующего уравнения (9.20), удовлетворяющее начальному условию у(л0) = >’0. На основании теоремы существования и единственности (см. теорему 1.1) такое решение существует и единственно в некоторой окрестности U к точки л:0.
Вычислим производную в точке М0. Согласно определению
первого интеграла, для решения у = у(л) имеем тождество где С0=(р<х0,у0).
Дифференцируя предыдущее равенство по .v, получим
В частности, для точки М0 имеем
Видео:Замена переменных в выражениях, содержащих частные производные (А.В. Бегунц)Скачать

Замена переменных
Выражения, содержащие различные функции и их производные, постоянно встречаются в математике и ее приложениях. Целесообразность перехода к новым независимым переменным, а иногда и к новым функциям, основана как на особой роли новых переменных в изучаемом вопросе, так и на упрощениях, к которым приводит выбранная замена переменных.
Техника замены переменных основана на правилах дифференцирования сложных функций и функций, заданных неявно при помощи уравнений. Такая техника будет продемонстрирована на нескольких достаточно содержательных примерах. Обоснование всех условий, при выполнении которых замена переменных будет законной, в большинстве примеров не представляет труда и поэтому не обсуждается.
В уравнении (displaystyle x^2+frac+xfrac+y=0) сделать замену независимой переменной (x=e^t).
(triangle) Если (z(t) = y(e^t)), то, применяя правило нахождения производной сложной функции, получаем
$$
frac=e^tfrac=xfrac,nonumber
$$
откуда (displaystyle frac=xfrac).
Заметим, что уравнение (displaystyle frac+z=0) является уравнением гармонических колебаний, а его решением является (z=C_sin t + C_2cos t). Поэтому при (x > 0) решение исходного уравнения имеет следующий вид: (y= C_1 sin (ln x) + C_2cos (ln x)). Так как уравнение не изменяет своего вида при замене (x) на (-x), то при любом (xin R, xneq 0), решение имеет следующий вид:
$$
y(x)=C_1sin(ln |x|) + C_2cos(ln |x|).qquadblacktrianglenonumber
$$
В системе уравнений:
$$
left<begindisplaystylefrac=y-2kx(x^2+y^2),\displaystylefrac=-x-2kx(x^2+y^2),\displaystyle k > 0,endright.nonumber
$$
перейти к полярным координатам.
(triangle) Умножим первое уравнение на (x), второе на (y) и сложим. Аналогично умножим первое уравнение на (y) и вычтем из него второе уравнение, умноженное на (x). Получим новую систему уравнений, при (x^2+y^2 > 0) эквивалентную исходной системе уравнений,
$$
left<begindisplaystyle xfrac+yfrac=-2k(x^2+y^2)^2,\displaystyle yfrac-xfrac=y^2+x^2.endright.label
$$
Но (x^2+y^2=r^2), (x=rcosvarphi), (y=rsinvarphi). Поэтому систему eqref можно записать в виде:
$$
left<begindisplaystyle rfrac=-2kr^4,\displaystylefrac=1.endright.Longleftrightarrowleft<begindisplaystylefrac=-2kr^3,\displaystylefrac=1.endright.label
$$
Заметим, что система eqref легко решается. Получаем решение в виде:
$$
r=frac<sqrt>,quad varphi=varphi_0+tquad (-t_0 Пример 3.
Преобразовать уравнение (y’y»’-3(y»)^2=x), принимая (y) за независимую переменную, а (x) — за неизвестную функцию.
Таким образом, при (y’neq 0) уравнение преобразуется к виду (x»’+x(x’)^5=0). Это частный случай уравнения общего вида (x»’=Phi(y,x,x’,x»)) с непрерывно дифференцируемой в (R^4) функцией (Phi(y,u,v,w)). Уравнения такого типа хорошо изучены в теории обыкновенных дифференциальных уравнений. Исходное уравнение не имело стандартного вида. (blacktriangle)
Преобразовать выражение (omega=displaystyle frac+frac) к полярным координатам, полагая (x=rcosvarphi, y=rsinvarphi). Найти решение уравнения Лапласа (displaystyle frac+frac=0), зависящее только от полярного радиуса (r).
Пусть (u=v(r)) есть решение уравнения Лапласа, зависящее только от (r). Тогда функция (v(r)) должна быть решением дифференциального уравнения
$$
frac+frac1rfrac=0quadLongleftrightarrowquadfracleft(rfracright)=0nonumber
$$
$$
rfrac=C,quadLongrightarrowquad v=C_1ln r+C_2,label
$$
где (C_1) и (C_2) — произвольные постоянные. (blacktriangle)
Сделать в уравнении колебаний струны
$$
frac-a^2frac=0,quad a > 0,quad -infty Решение.
Решение уравнения (displaystylefrac=0) легко находится. Так как (displaystylefracpartialleft(fracright)=0), то (displaystylefrac=varphi(eta)), где (varphi(eta)) — произвольная непрерывная функция (eta).
Пусть (Phi(eta)) есть ее первообразная на (R). Тогда, интегрируя уравнение (omega_=varphi(eta)), получаем, что (omega=Phi(eta)+Psi(xi)), где (Psi(xi)) — произвольная функция.
Если считать, что функции (Phi(eta)) и (Psi(xi)) есть непрерывно дифференцируемые функции, то общее решение уравнения eqref имеет следующий вид:
$$
u(x,t)=Psi(x-at)+Phi(x+at).quadblacktrianglenonumber
$$
Видео:13.10.2023 Практика 8. Замена переменных в уравнениях в частных производныхСкачать

Частные производные
Назначение сервиса . Сервис используется для нахождения частных производных функции (см. пример). Решение производится в онлайн режиме и оформляется в формате Word .
- Решение онлайн
- Видеоинструкция
- Также решают
Правила ввода функции, заданной в явном виде
- Примеры
x 2 +xy ≡ x^2+x*y .
cos 2 (2x+y) ≡ (cos(2*x+y))^2≡ (x-y)^(2/3)
Правила ввода функции, заданной в неявном виде
- Все переменные выражаются через x,y,z
- Примеры
≡ x^2/(z+y)
cos 2 (2x+zy) ≡ (cos(2*x+z*y))^2≡ z+(x-y)^(2/3)
Видео:Математика без Ху!ни. Частные производные функции нескольких переменных. Градиент.Скачать

Частные производные функции нескольких переменных
Пример 1 . z=2x 5 +3x 2 y+y 2 –4x+5y-1
Пример 2 . Найти частные производные 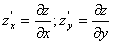
Находим частные производные:
Найдем частные производные в точке А(1;1)
Находим вторые частные производные:
💡 Видео
Частные производные функции многих переменныхСкачать

Алгебра Система уравнений Метод замены переменной № 6.22 9 классСкачать

Замена переменной в дифференциальных выражениях. Постановка задачи. Замена независимых переменных.Скачать

Решение уравнения методом замены переменнойСкачать

Шишкин А. А. - Математический анализ II - Замена переменных в выражениях с производнымиСкачать

Математический анализ, 29 урок, Функции нескольких переменных. Частные производныеСкачать

28.09.2023 Практика 7. Замена переменных в дифференциальных уравненияхСкачать

Могилевский И. Е. - Математический анализ II - Замена независимых переменныхСкачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Математический анализ, 42 урок, Замена переменных в двойном интегралеСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Замена переменных в дифференциальных уравнениях.Скачать

Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

Математический анализ, 20 урок, Метод замены переменнойСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать














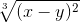 ≡ (x-y)^(2/3)
≡ (x-y)^(2/3)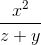 ≡ x^2/(z+y)
≡ x^2/(z+y) 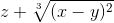 ≡ z+(x-y)^(2/3)
≡ z+(x-y)^(2/3)