Замена переменных и приведение к линейному уравнению парной регрессии (2 видео)

ПРИВЕДЕНИЕ ИСХОДНОГО НЕЛИНЕЙНОГО УРАВНЕНИЯ РЕГРЕССИИ К ЛИНЕЙНОМУ

О лабораторной работе № 2

на тему:

«Определение параметров нестационарного нелинейного уравнения регрессии»

2 курса 221 группы

Содержание

2.ПРИВЕДЕНИЕ ИСХОДНОГО НЕЛИНЕЙНОГО УРАВНЕНИЯ РЕГРЕССИИ К ЛИНЕЙНОМУ………………………………………………………………………………………7 3.ПРОВЕРКА НАЛИЧИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ МЕЖДУ ФАКТОРАМИ МОДЕЛИ……………………………………………………………………………………………8

4.ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ УРАВНЕНИЯ РЕГРЕССИИ. ПОСТРОЕНИЕ УРАВНЕНИЯ РЕГРЕССИИ………………………………………………………………………11

5.ПРОВЕРКА СТАТИСТИЧЕСКОЙ ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ ………. 13

5.1.Проверка случайности колебаний уровней статочной последовательности………. 13

5.2. Проверка соответствия распределения случайной компоненты нормальному закону распределения……………………………………………………………………………………15

5.3.Проверка равенства математического ожидания случайной компоненты нулю………..16

5.4.Проверка независимости значений уровней случайной компоненты……………………17

5.5.Определение точности модели………………………………………………………………18

5.6. Тест ранговой корреляции Спирмена ……………………………………………………….19

6. ПРОВЕРКА НАЛИЧИЯ АНОМАЛЬНЫХ КОЛЕБАНИЙ ИССЛЕДУЕМОЙ МОДЕЛИ..21

7.ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО ВИДА ЛИНИИ ТРЕНДА. ПРОГНОЗ ПОКАЗАТЕЛЕЙ…………………………………………………………………………………..22

Список использованной литературы………………………………………………25

ВВЕДЕНИЕ

Специфической особенностью деятельности экономиста является работа в условиях недостатка информации и неполноты исходных данных. Анализ такой информации требует специальных методов, которые составляют один из аспектов эконометрики. Центральной проблемой эконометрики является построение эконометрической модели и определение возможностей ее использования для описания, анализа и прогнозирования реальных экономических процессов.

Становление и развитие эконометрического метода происходили на основе так называемой высшей статистики — на методах парной и множественной регрессии, парной, частной и множественной корреляции, выделения тренда и других компонент временного ряда, на статистическом основании.

Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целого ряда других вопросов эконометрики. В настоящее время множественная регрессия — один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии — построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.

Задачей данной работы является оценка адекватности и точности нелинейной нестационарной модели уравнения регрессии с использованием персональных компьютеров.

Данная работа состоит из семи глав и трех приложении. Первая глава – постановка задачи.

Во второй главе осуществляется приведение исходного нелинейного уравнения регрессии к линейному по средствам замены переменных.

В третьей главе проверяется наличие мультиколлинеарности между факторами модели.

В главе 4 определяются параметры уравнения регрессии и строится искомое уравнение регрессии.

В пятой главе проверяется статистическая значимость уравнения регрессии. В пункте 5.1. осуществляется проверка колебаний уровней остаточной последовательности при помощи критерия серий, основанного на медиане выборки. В пункте 5.2. проводится проверка соответствия распределения случайной компоненты нормальному закону распределения при помощи показателей ассиметрии и эксцесса. В пункте 5.3. показана проверка равенства математического ожидания случайной компоненты нулю с использованием t-критерия Стьюдента. В пункте 5.4. проверяется независимость значений уровней случайной компоненты с целью выявления существующей автокорреляции остаточной последовательности. В данной работе эта проверка производится при помощи d-критерия Дарбина — Уотсона. В пункте 5.5. определяется точность модели. В качестве статистических показателей точности в данной работе используются следующие: среднеквадратичное отклонение, средняя относительная ошибка аппроксимации, коэффициент сходимости, коэффициент детерминации. В пункте 5.6 проверяется наличие или отсутствие гетероскедастичности исследуемой модели при помощи теста ранговой корреляции Спирмена.

В шестой главе осуществляется проверка на наличие аномальных колебании исследуемой модели с помощью метода Ирвина.

В восьмой главе определяется оптимальный вид линии тренда, которые отражены в приложениях, и прогнозируются показатели.

ПОСТАНОВКА ЗАДАЧИ

В данной работе необходимо рассмотреть нелинейную нестационарную модель изучаемого экономического объекта. В качестве объекта исследования представлен экономический процесс, о котором известны следующие статистические данные:

1. Y(t) — ставка % рефинансирования Центробанка;

2. X₁(t) — уровень безработицы, %

3. X₂(t) — уровень инфляции, %

Требуется найти коэффициенты нелинейной нестационарной модели уравнения множественной регрессии вида:

Y(t) — ставка % рефинансирования Центробанка;

X₁(t) — уровень безработицы, %

X₂(t) — уровень инфляции, %

Значения величин Y(t), X₁(t), Х₂(t) даны в Таблице №1 «Исходные данные». Данное нелинейное уравнение требуется привести к линейному уравнению вида:

(2)

Ø определить параметры уравнения регрессии, используя замену переменной;

Ø проверить наличие мультиколлинеарности между факторами;

Ø проверить статистическую значимость уравнения в целом и отдельных коэффициентов уравнения. Это позволит оценить адекватность полученной модели исследуемому процессу и возможность её использования для осуществления анализа и проектирования;

Ø проверить отсутствие гетероскедастичности и автокорреляции остатков исследуемой модели, установить адекватность и точность уравнения регрессии;

Ø проверить наличие аномальных наблюдений, используя метод Ирвина.

Таблица №1

ИСХОДНЫЕ ДАННЫЕ

T	X₁	X₂	Y
25,22
21,52
22,32
21,77
20,66
20,14
17,66
17,08
16,87
18,63
16,51
16,95
19,38
18,14
17,94
19,69
19,38
15,88
16,58
14,64

ПРИВЕДЕНИЕ ИСХОДНОГО НЕЛИНЕЙНОГО УРАВНЕНИЯ РЕГРЕССИИ К ЛИНЕЙНОМУ

Многие экономические процессы наилучшим образом описываются нелинейными уравнениями регрессии. Например, функции спроса и производственные функции. И в этом случае мы не можем применить к ним обычный метод наименьших квадратов и использовать стандартные подходы к оценке статистической надежности.

В связи с этим встает задача о возможности привести нелинейное уравнение к линейному виду.

В тех случаях, когда нелинейность касается факториальных переменных, но не связано с коэффициентами уравнения регрессии, нелинейность обычно устраняется путем замены переменной.

Рассмотрим нелинейное нестационарное уравнение:

Y(t) — ставка % рефинансирования Центробанка;

X₁(t) — уровень безработицы, %

X₂(t) — уровень инфляции, %

В данном случае нелинейность касается факторных переменных, но не связано с коэффициентами уравнения.

Вводим новые переменные:

Полученное уравнение является линейным как по переменным, так и по параметрам.

Содержание

Уравнение нелинейной регрессии
Виды нелинейной регрессии
Модель парной нелинейной регрессии
Линеаризация уравнения регрессии и оценка результатов моделирования
💡 Видео

Видео:Эконометрика. Линейная парная регрессияСкачать

Уравнение нелинейной регрессии

Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии

Видео:Парная регрессия: линейная зависимостьСкачать

Виды нелинейной регрессии

Вид	Класс нелинейных моделей
Полиномальное уравнение регрессии: y = a + bx + cx 2 (см. метод выравнивания) Гиперболическое уравнение регрессии: Квадратичное уравнение регрессии:	Нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам
Показательное уравнение регрессии: Экспоненциальное уравнение регрессии: Степенное уравнение регрессии: Полулогарифмическое уравнение регрессии: y = a + b lg(x)	Нелинейные по оцениваемым параметрам

Здесь ε — случайная ошибка (отклонение, возмущение), отражающая влияние всех неучтенных факторов.

Уравнению регрессии первого порядка — это уравнение парной линейной регрессии.

Уравнение регрессии второго порядка это полиномальное уравнение регрессии второго порядка: y = a + bx + cx 2 .

Уравнение регрессии третьего порядка соответственно полиномальное уравнение регрессии третьего порядка: y = a + bx + cx 2 + dx 3 .

Чтобы привести нелинейные зависимости к линейной используют методы линеаризации (см. метод выравнивания):

Замена переменных.
Логарифмирование обеих частей уравнения.
Комбинированный.

y = f(x)	Преобразование	Метод линеаризации
y = b x a	Y = ln(y); X = ln(x)	Логарифмирование
y = b e ax	Y = ln(y); X = x	Комбинированный
y = 1/(ax+b)	Y = 1/y; X = x	Замена переменных
y = x/(ax+b)	Y = x/y; X = x	Замена переменных. Пример
y = aln(x)+b	Y = y; X = ln(x)	Комбинированный
y = a + bx + cx 2	x₁ = x; x₂ = x 2	Замена переменных
y = a + bx + cx 2 + dx 3	x₁ = x; x₂ = x 2 ; x₃ = x 3	Замена переменных
y = a + b/x	x₁ = 1/x	Замена переменных
y = a + sqrt(x)b	x₁ = sqrt(x)	Замена переменных

Пример . По данным, взятым из соответствующей таблицы, выполнить следующие действия:

Построить поле корреляции и сформулировать гипотезу о форме связи.
Рассчитать параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессии.
Оценить тесноту связи с помощью показателей корреляции и детерминации.
Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
Оценить с помощью средней ошибки аппроксимации качество уравнений.
Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выбрать лучшее уравнение регрессии и дать его обоснование.
Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 15% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α=0,05 .
Оценить полученные результаты, выводы оформить в аналитической записке.

Год	Фактическое конечное потребление домашних хозяйств (в текущих ценах), млрд. руб. (1995 г. — трлн. руб.), y	Среднедушевые денежные доходы населения (в месяц), руб. (1995 г. — тыс. руб.), х
1995	872	515,9
2000	3813	2281,1
2001	5014	3062
2002	6400	3947,2
2003	7708	5170,4
2004	9848	6410,3
2005	12455	8111,9
2006	15284	10196
2007	18928	12602,7
2008	23695	14940,6
2009	25151	16856,9

Решение. В калькуляторе последовательно выбираем виды нелинейной регрессии. Получим таблицу следующего вида.
Экспоненциальное уравнение регрессии имеет вид y = a e bx
После линеаризации получим: ln(y) = ln(a) + bx
Получаем эмпирические коэффициенты регрессии: b = 0.000162, a = 7.8132
Уравнение регрессии: y = e 7.81321500 e 0.000162x = 2473.06858e 0.000162x

Степенное уравнение регрессии имеет вид y = a x b
После линеаризации получим: ln(y) = ln(a) + b ln(x)
Эмпирические коэффициенты регрессии: b = 0.9626, a = 0.7714
Уравнение регрессии: y = e 0.77143204 x 0.9626 = 2.16286x 0.9626

Гиперболическое уравнение регрессии имеет вид y = b/x + a + ε
После линеаризации получим: y=bx + a
Эмпирические коэффициенты регрессии: b = 21089190.1984, a = 4585.5706
Эмпирическое уравнение регрессии: y = 21089190.1984 / x + 4585.5706

Логарифмическое уравнение регрессии имеет вид y = b ln(x) + a + ε
Эмпирические коэффициенты регрессии: b = 7142.4505, a = -49694.9535
Уравнение регрессии: y = 7142.4505 ln(x) — 49694.9535

Видео:Множественная регрессияСкачать

Модель парной нелинейной регрессии

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.

Различают два класса нелинейных регрессий:

1. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например

— полиномы различных степеней — , ;

— полулогарифмическая функция — .
2. Регрессии, нелинейные по оцениваемым параметрам, например
— степенная — ;

Регрессии нелинейные по включенным переменным приводятся к линейному виду простой заменой переменных, а дальнейшая оценка параметров производится с помощью метода наименьших квадратов.

Видео:Эконометрика Линейная регрессия и корреляцияСкачать

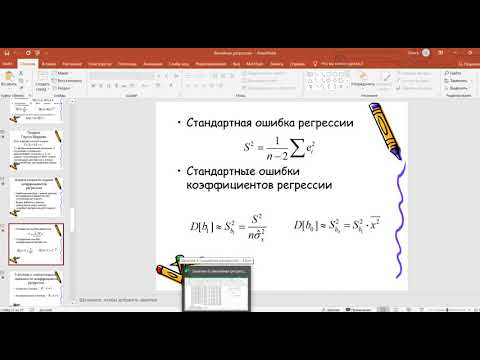
Линеаризация уравнения регрессии и оценка результатов моделирования

Приведение к линейному виду регрессий, нелинейных по объясняющим переменным

Нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Она определяется, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам. Так, в параболе второй степени

заменяя переменные х1 =х, х2 = х2, получим двухфакторное уравнение линейной регрессии:

для оценки параметров которого, как будет показано далее, используется МНК.

Приведение к линейному виду регрессий, нелинейных по параметрам

Данный класс нелинейных моделей подразделяется на два типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные.

Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду.

Если нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции.

В специальных исследованиях по регрессионному анализу часто к нелинейным относят модели, только внутренне нелинейные по оцениваемым параметрам, а все другие модели, которые внешне нелинейны, но путем преобразований параметров могут быть приведены к линейному виду, относятся к классу линейных моделей.

В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразованным уравнениям.

Если в линейной модели и моделях, нелинейных по переменным, при оценке параметров исходят из критерия

то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным данным результативного признака, а к их преобразованным величинам, т. е. lпу, 1/у.

Вследствие этого оценки параметров для линеаризуемых функций МНК оказываются несколько смещенными.

Оценка результатов эконометрического моделирования достигается посредством решения качественной и количественной проблемы. Качественная составляющая заключается в установлении соответствия между построенной моделью и основополагающей экономической концепцией, а количественная — в точности аппроксимации имеющейся информации данными расчётов.