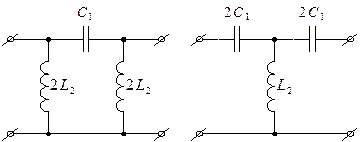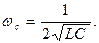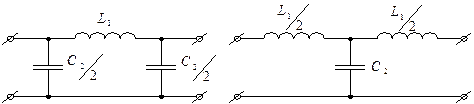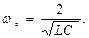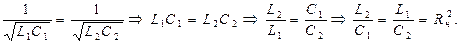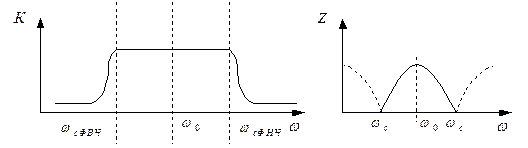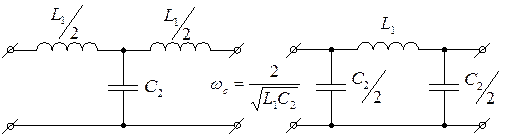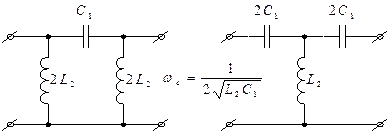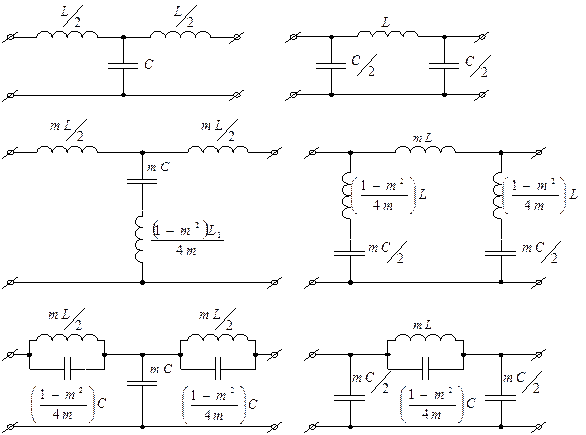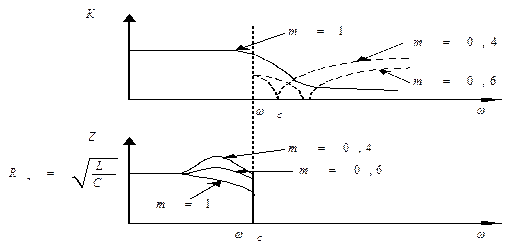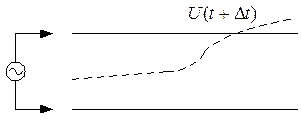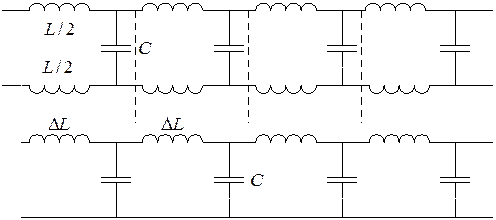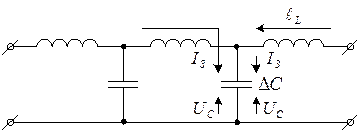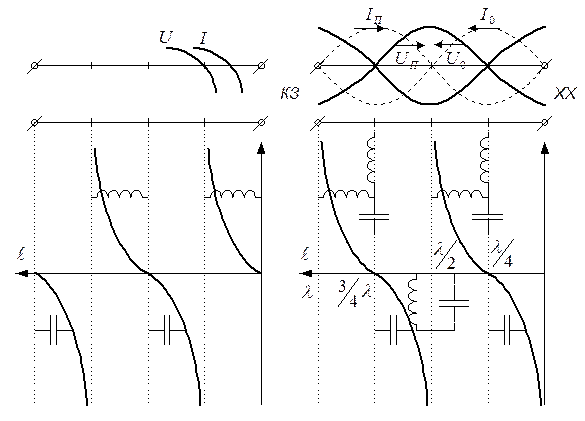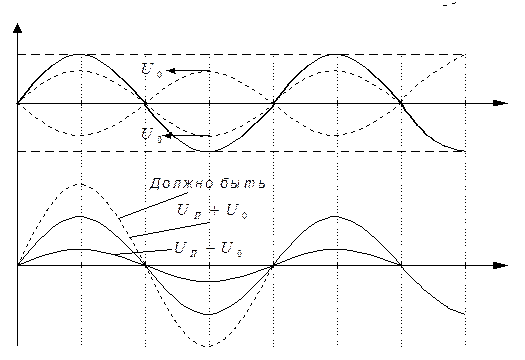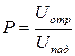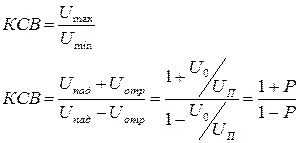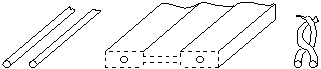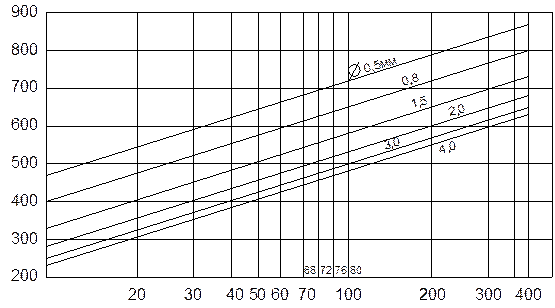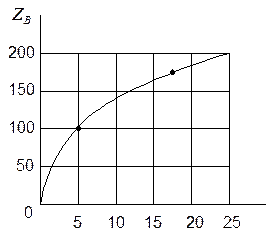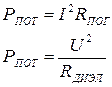Калькулятор расчёта полосно-заграждающих Т-образных и П-образных LC-фильтров.
Что такое режекторный фильтр (он же полосно-заграждающий, он же — фильтр-пробка) и с чем его едят, мы определились на предыдущей странице, рассматривая пассивные и активные режекторные RC-фильтры.
Так же, как и в случаях с НЧ, ВЧ и полосовыми собратьями, LC режекторные фильтры обладают рядом достоинств, таких как: высокая стабильность, низкий уровень собственных шумов, а также возможность работы с широким спектром сигналов, включая СВЧ диапазоны.
Простейший представитель режекторного LC-фильтра 2-го порядка представлен на Рис.1. 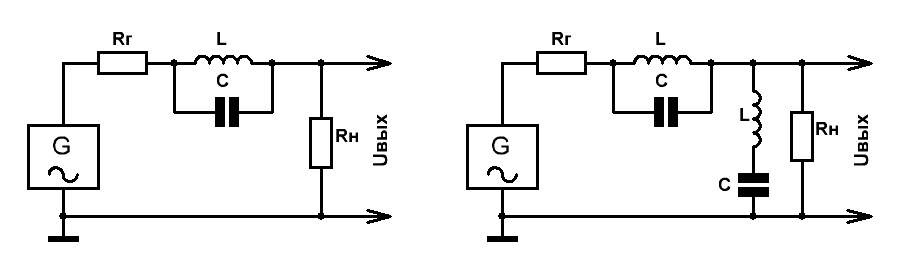
Рис.1 
Логика работы такого фильтра предельно проста.
На резонансной частоте fо= 1/2π√ LС сопротивление параллельного колебательного контура, образованного катушкой индуктивности L и конденсатором C, принимает максимальное значение, соответственно максимальное значение принимает и коэффициент подавления сигнала на этой частоте.
Глубина режекции (подавления частоты fo) этого фильтра при работе на согласованную нагрузку, равную характеристическому сопротивлению колебательного контура ρ = √ L/C , достигает 45 дБ.
На Рис.2 представлена схема Г-образного режекторного фильтра 4-го порядка.
Принцип работы этого фильтра основан на использовании резонансов напряжений и токов в последовательных и параллельных колебательных контурах. На частоте резонанса сопротивление параллельного плеча оказывается максимальным, а последовательного – минимальным, что и соответствует наибольшему затуханию цепи.
Глубина режекции в данной схеме уже может составлять величину 90 дБ.
Приведём таблицу для расчёта элементов этих фильтров.
Не забываем, что характеристическое сопротивление фильтра ρ должно равняться Rг =Rн.
ТАБЛИЦА РАСЧЁТА ЭЛЕМЕНТОВ РЕЖЕКТОРНЫХ LC- ФИЛЬТРОВ 2-го и 4-го ПОРЯДКОВ
Для получения больших значений подавления центральной частоты (глубины режекции) используют два или более Г-образных звеньев, соединяя их последовательно, чтобы образовать Т-образное звено, или П-образное звено.
На Рис.3 приведены схемы типовых полосно-заграждающих LC-фильтров 6-го порядка Т-образной (слева) и П-образной (справа) структур с глубиной режекции — около 130 дБ. 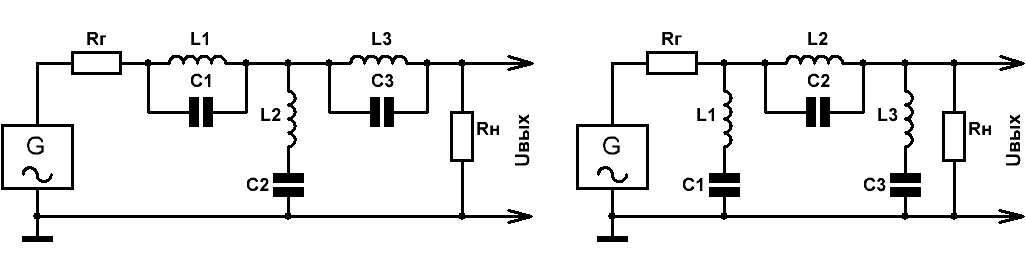
Рис.3
Ничего не изменилось — последовательная ветвь обладает минимальным полным сопротивлением и оказывает шунтирующее воздействие на центральной частоте диапазона. Ее полное сопротивление начинает увеличиваться по обе стороны от частоты резонанса.
Параллельная же ветвь на центральной частоте имеет максимальное сопротивление, и оно уменьшается по обе стороны резонанса.
Центральная частота режекции равна fо= 1/2π√ LС , характеристическое сопротивление ρ = √ L/C , а значения частотозадающих элементов рассчитываются исходя из следующих равенств:
L1 = L3 = L/2, L2 = L, C1 = C3 = C×2, C2 = C для Т-образного фильтра,
L1 = L3 = L×2, L2 = L, C1 = C3 = C/2, C2 = C для П-образного фильтра.
Приведём таблицу для расчёта элементов и этих фильтров.
ТАБЛИЦА РАСЧЁТА ЭЛЕМЕНТОВ РЕЖЕКТОРНЫХ Т- и П-образных LC- ФИЛЬТРОВ
Ширина полосы задержания представленных режекторных LC-фильтров составляет величину, примерно равную 50% от значения центральной частоты fo.
Видео:Лекция 66. Фильтр низкой частотыСкачать

Заграждающие фильтры
Заграждающий фильтр пропускает сигналы, частоты которых находятся выше и ниже установленной полосы задерживания. Поэтому фильтр такого типа задерживает составляющие сигнала в окрестности некоторой частоты. Так же, как и в полосовом фильтре, ширина полосы задерживания заграждающего фильтра определяется добротностью Q используемой цепи. Соображения, касающиеся добротности и частоты резонанса полосового фильтра, а также приведенные в разд. 5.7 формулы для этих величин справедливы и для заграждающего фильтра.
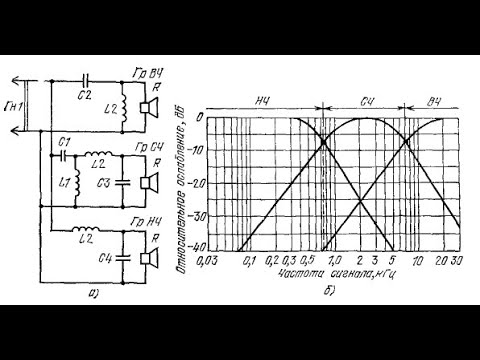
На рис. 5.7, а показана основная схема Г-образного заграждающего фильтра типа k. Предположим, что цепи параллельного и последовательного резонансов настроены в резонанс на центральную частоту fр полосы сигналов, которые необходимо задержать. В таком случае цепь параллельного резонанса L1C1 создает высокий импеданс для сигналов на резонансной частоте и поэтому ослабляет их. В то же время прошедшие через параллельный контур сигналы шунтируются на выходе низким импедансом цепи последовательного резонанса L2C2. Для составляющих же сигнала с частотами выше и ниже резонансной частоты контур параллельного резонанса L1С1 имеет низкий импеданс и незначительно ослабляет эти сигналы.
В то же время составляющие сигнала, частоты которых отличаются от резонансной для цепи L2C2, незначительно ослабляются этой цепью из-за большой величины импеданса этой цепи.
На рис. 5.7,6 показана частотная характеристика заграждающего фильтра. Частота fi соответствует нижней частоте полосы задерживания, а частота fz — верхней. Эта характеристика представляет собой перевернутую кривую избирательности, и ширина полосы задерживания определяется здесь аналогично тому, как это было показано для полосы пропускания полосового фильтра.
Рис. 5.7. Заграждающие фильтры и их частотная характеристика.
На рис. 5.7, в изображена схема П-образного заграждающего фильтра, а на рис. 5.7, г — схема Т-образного фильтра.
Величины элементов заграждающего фильтра находят по формулам
В этих формулах RH, как и раньше, является активным сопротивлением нагрузочного элемента заграждающего фильтра.
Видео:Лекция 72. Режекторный фильтр.Скачать

Полосовые и заградительные фильтры типа “К”.
На основе ФВЧ и ФНЧ типа “К” (LC) можно построить полосовые и режекторные фильтры.
1) Полосовые фильтры
Полосовые фильтры реализуют с помощью Т и П звеньев, при последовательном включении ФВЧ и ФНЧ. Такие фильтры не обеспечивают хороших характеристик, так как в полосе пропускания, вблизи ω0, входное сопротивление зависит от частоты, а в полосе задержания входное сопротивление резистивное, то есть нарушается условие согласования.
Чаще всего в качестве полосовых применяются фильтры на основе LC контуров.
У такого фильтра, при увеличении в сторону от резистивного, сопротивление последовательного звена увеличивается, а параллельного падает на резистивной частоте, входное сопротивление фильтров активное и равно Rн. На частотах ниже резонансной последовательный контур имеет активно – емкостной характер, а параллельно – индуктивный, то есть полосовой, фильтр превращается в ФВЧ типа “К”.
Частота среза ωс будет зависеть от С1 и L2:
На частотах выше ωрез последовательный контур имеет индуктивный характер, а на параллельный – емкостное сопротивление т.е. полосовой фильтр превращается в фильтр типа “К”.
Частота среза ωс будет зависеть от L1 и С2:
Если последовательный и параллельный контур имеют одинаковую ωс, то:
Тогда сохраняя эту пропорцию можно изменить величины C1L2=C2L1, то есть уменьшать частоты среза ФВЧ и ФНЧ в зависимости от того какая требуется полоса. В полосе пропускания входное сопротивление чисто активное, а вне полосы реактивное. На резонансной частоте ω0 входное сопротивление равно Rн.
2) Заградительные фильтры.
Как и полосовые, выполняются на LC контурах, только последовательные и параллельные контура меняются местами.
На частотах ниже резонансной параллельный колебательный контур имеет индуктивный характер, а последовательный емкостное сопротивление т.е. полосовой фильтр превращается в ФНЧ.
На частотах выше резонансной соответственно полосовой фильтр преобразуется в ФВЧ.
Частота среза ФНЧ 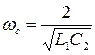
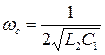
Фильтры типа “М”.
Если в ФВЧ или ФНЧ типа “К” часть реактивного сопротивления из параллельного звена перенесена в последовательный или наоборот, то фильтр типа “К” превращается в фильтр типа “М”. Коэффициент “М” показывает, какая часть реактивного сопротивления осталась в последовательном или параллельном звене. Например ФНЧ типа “К” можно преобразовать в ФНЧ типа “М”.
Особенностью ФНЧ типа “М” является то , что он имеет более прямую АЧХ в области частоты среза. Это вызвано наличием резонансного контура (последовательного или параллельного), частота которого выше на некоторую величину зависящую от “М”, чем частота среза.
При m=1 фильтр является фильтром типа “К”. При малых “m” крутизна АЧХ вблизи ωС очень большая, но при более высокой частоте в полосе задержания коэффициент передачи больше, чем при больших “m”.
Входное сопротивление фильтра типа “М” вблизи ωС зависит от “m”. При m=0,6 входное сопротивление наиболее равномерно в полосе пропускания.
Длинными линиями называются электрические цепи, геометрические размеры которых, соизмеримы с длиной волны в этих цепях.
Если к двухпроводной линии подключить источник постоянного напряжения, то на выходе линии напряжение появится не сразу, а спустя некоторое время. Это связано с тем, что между проводами линии существует электрическая емкость, а сами провода обладают индуктивностью. Причем емкость и индуктивность распределены по всей длине линии равномерно в виде бесконечно большого числа бесконечно малых конденсаторов и катушек. При подключении источника Е напряжение на каждом элементарном конденсаторе (ΔС) не может появиться мгновенно, так как заряжаются конденсаторы через элементарные индуктивности (ΔL), причем заряжаются тем дольше, чем больше ΔL и ΔС. Каждый последующий конденсатор может зарядится только после того, как зарядится предыдущий. Таким образом, напряжение на выходе линии появится лишь тогда, когда зарядится последний конденсатор ΔС. Чем длиннее линия, тем больший промежуток времени пройдет прежде чем на выходе линии установится напряжение, подведенное к ее входу, так как тем большая индуктивность проводов и емкость между ними.
Для каждой конкретной линии в зависимости от сечения проводов и расстояния между ними (а также μ и Е) существует вполне определенная индуктивность и емкость на 1 метр длинны. Эти величины называются погонными индуктивностью и емкостью L и С.
Если ко входу линии подключить источник переменного напряжения, то при достаточно большой длине линии напряжение на выходе ее достигнет величины которая была в момент включения на входе лишь спустя некоторое время Δt, но за это время напряжение на входе линии уже изменится. Стечением времени напряжение на выходе также изменится в соответствии с изменением на входе. Чем меньше период колебаний входного напряжения, тем больше будут отличаться входное и выходное напряжение. Если период колебаний достаточно большой по сравнению с временем Δt задержки выходного напряжения, то напряжение на выходе практически повторяет напряжение на входе. Если же период колебаний уменьшать, то напряжение на выходе будет отставать по фазе от входного, когда Δt будет равно Т/2, а напряжение на выходе будет в противофазе с входным (а в середине линии напряжение между проводами не будет равно 0).
Каждая практическая линия предназначена для передачи энергии от источника в нагрузку. Всякую линию можно представить эквивалентной схемой состоящей из элементарных индуктивностей ΔL и емкостей ΔС.
Если нагрузкой линии будет активное сопротивление 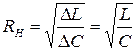
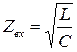
Если линия нагружена на активное сопротивление равное волновому, то вся энергия, поступающая от источника в линию, поглощается нагрузкой, при это в линии движется электромагнитная волна, которую называют падающей.
В любом сечении линия имеет активное сопротивление 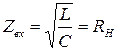
Режимы работы длинных линий
Когда линия нагружена на активное сопротивление, равное ее волновому, вся энергия входящая в линию доходит до нагрузки и поглощается ею. Такой режим работы линии называется режимом бегущих волн. В этом режиме ток и напряжение совпадает по фазе по всей длине линии.
Если сопротивление нагрузки не равно волновому, то часть энергии от нагрузки отразится и вернется в источник. В этом случае падающая волна (энергия) дойдя до нагрузки частично поглощается и частично отражается. Отраженная энергия переносится отраженной волной движущейся на встречу падающей. Такой режим работы длинных линий называется режимом смешанных волн.
Если сопротивление ≠ 0 или ∞, то энергия нагрузки не поглощается, а полностью возвращается источнику отраженной волной.
При холостом ходе (ХХ) отраженная волна должна обеспечить в конце линии ток ≠ 0. Для этого ЭДС отраженной волны в конце линии должна быть равна ЭДС падающей как по амплитуде, так и по фазе. Появление отраженной волны можно объяснить тем, что ток исчезнув в конце линии, навел в последнем элементарном участке ΔL ЭДС самоиндукции, которая заряжает последний элементарный конденсатор ΔС до удвоенного напряжения.
Отраженная волна двигаясь на встречу падающей взаимодействует с ней. В точке удаленной на расстоянии 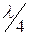
На расстоянии 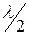
На расстоянии 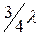
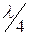
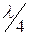
Режим линии, при котором U и І в узлах всегда равны нулю, а в пучностях изменяются от нуля до максимума называют режимом стоячих волн.
Для линии с коротким замыканием (КЗ) на конце пучности и узлы также располагаются в зависимости от конца линии.
Новотраженной волне напряжение в конце линии находится в противофазе с падающей волной, поэтому узлы и пучности напряжения расположены там, где у разомкнутой линии находится узлы и пучности тока.
Расположение узлов и пучностей при КЗ или ХХ всегда определяется концом линии и не зависит от длинны линии.
В отличии от режима бегущих волн, в режиме стоячих волн U и I на совпадают по фазе (разнится на 90 0 ), значит входное сопротивление линии при КЗ и ХХ имеет реактивный характер. Причем характер входного сопротивления (емкостной или индуктивный) зависит от расстояния до конца линии, т. е. от длинны линии (при неизменной длине волны электрического сигнала).
У линии разомкнутой на конце в точках 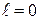
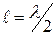
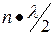
В точках 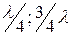
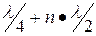
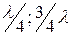
У линии замкнутой на конце характер изменения сопротивления, как бы сдвинут на 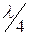
В реальных линиях амплитуда падающей и отраженной волн не одинакова по всей длине линии, поэтому при удалении от конца линии сумма падающей и отраженной волны уже не равна удвоенному значению, а разница не равна нулю.
В практике эксплуатации линий кроме режимов ХХ, КЗ и согласованного существуют и другие.
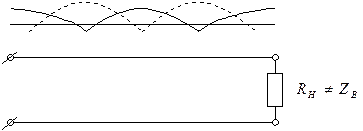
Например, если сопротивление нагрузки RН активное, но больше или меньше, чем волновое сопротивление линии ZВ, то амплитуда отраженной волны меньше чем падающей, а это значит, что сумма и разность падающей и отраженной волн не бывают удвоенной или нулевой.
Чем больше отличается RН от ZB, тем больше режим напоминает ХХ или КЗ. Для оценки режимов существует коэффициент отражения
и коэффициент стоячей волны
Если нагрузка представляет собой реактивное сопротивление (С или L), то как и в режиме ХХ и КЗ вся энергия будет отражаться, но распределение токов и напряжений будет другим. Конденсатор в конце линии можно заменить отрезком меньше, чем 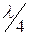
Индуктивную нагрузку можно заменить отрезком КЗ линии длиной от 0 до 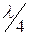
Фидерами называются длинные линии, специально предназначенные для передачи без потерь энергии от источника сигнала в нагрузку (например, от передатчика в антенну или от антенны к приемнику) т. е. фидеры это длинные линии, которые должны работать в режиме бегущих волн.
В качестве фидера можно использовать не только двухпроводные линии с воздушным диэлектриком, провода линии могут быть запрессованы в диэлектрик (ленточный кабель) или свиты в спираль, если каждый провод имеет изоляцию.
Существуют также четырехпроводные фидеры, у которых две двухпроводные линии соединены параллельно, и коаксиальные фидеры, у которых один провод находится внутри другого, как в оболочке.
Наиболее простыми являются открытые двухпроводные фидеры. У этих фидеров волновое сопротивление зависит от расстояния между проводами и диаметра проводов. Для фиксации расстояния между проводами, провод скрепляется изолирующими распорками через определенные промежутки длины.
Теоретические расчеты показывают, что волновое сопротивление открытой двухпроводной линии не может быть менее 200 Ом. Практически для определения ZВ открытой двухпроводной линии можно пользоваться специальным графиком.
Недостатками открытой двухпроводной линии является подверженность климатическим воздействиям и сравнительно большое ZВ, которое не согласуется с большинством практических антенн (имеющих свое входное активное сопротивление).
Двухпроводные линии запрессованные в диэлектрик не подвержены атмосферным воздействиям и имеют меньшее ZВ благодаря тому, что у диэлектрика ε > 1 т. е. больше погонная емкость. Но у опрессованных линий больше потери энергии т. к. любой диэлектрик имеет худшие диэлектрические (изолирующие) свойства чем, воздух. Промышленность выпускает несколько разновидностей опрессованных линий с волновым сопротивлением от 50 до 300 Ом, что позволяет использовать их для различных типов антенн.
Если две двухпроводные линии соединить параллельно, то волновое сопротивление такой линии будет в 2 раза меньше, чем у двухпроводной, а линия будет называться четырехпроводной.
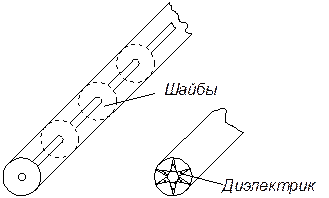
Коаксиальные фидеры обычно делают гибкими, а промежуток между внутренним проводом заполняют изолятором. Чтобы потери были меньше, в качестве изолятора применяют керамические шайбы, либо диэлектрик делают ребристым.
Коаксиальные фидеры относятся к числу несимметричных фидеров (провода неравнозначны по отношению к земле).
Внешняя оболочка (оплетка) обычно заземляется, причем она может быть изолирована слоем диэлектрика. Достоинством коаксиальных фидеров является то, что очень удобны в эксплуатации, кроме того, отсутствуют потери на излучение энергии.
Волновое сопротивление коаксиальных фидеров зависит от соотношения диаметров наружного и внутреннего проводов и диэлектрической проницаемости диэлектрика.
Промышленность выпускает в основном коаксиальные фидеры (кабели) с ZВ 50 и 70 Ом.
Согласование фидеров с нагрузкой
Если сопротивление нагрузки не равно ZВ фидера, то не вся энергия отдается в нагрузку, в фидере образуется стоячая волна и резко возрастают потери в активном сопротивлении линии и диэлектрике.
Кроме этого отраженные волны иногда просто недопустимы т. к. искажают сигнал (например, двоение в TV).
В практике далеко не всегда сопротивление нагрузки равно ZВ имеющейся линии, тем более, что промышленностью выпускаются линии со стандартными значениями ZВ (например, в 50, 75, 100 Ом и т. д.), а RН может быть самым разнообразным. Поэтому для обеспечения высокого КПД т. е. согласованной нагрузки применяют специальные согласующие устройства.
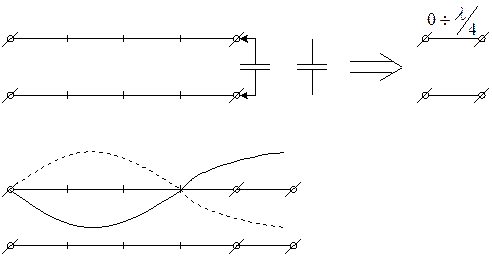
Если сопротивление нагрузки активное, но не равное ZВ, то чаще всего для согласования применяют, так называемый четвертьволновой трансформатор.
Суть такого трансформатора состоит в том, что входное сопротивление линии длиной 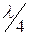
Дата добавления: 2016-03-15 ; просмотров: 3866 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
📹 Видео
Частотные фильтрыСкачать

ВЧ-фильтры. Часть 2. ФНЧ ФВЧ. Начинающим радиоконструкторам. Ликбез.Скачать

0072. Режекторный фильтрСкачать

Колебательный контур и полосно-заграждающий фильтрСкачать

Как работает Электрический ФИЛЬТР РЕАЛЬНО | Часть 1Скачать
9) ТАУ для чайников. Части 3.7 и 3.8: Частотные характеристики.Скачать

Фильтры низкой и высокой частоты для динамика.Как они работают,схемаСкачать

Аналоговые фильтрыСкачать

Всё что нужно знать о фильтрах в акустических системахСкачать
14.Лавренов Н.В. Фильтры верхних частот, фильтры нижних частот и полосовые фильтры.Скачать

ВЧ фильтры. Часть 1. Что это такое? Какие бывают? Начинающим радиоконструкторам. Ликбез.Скачать

Что такое АЧХ(Амплитудно Частотная Характеристика)Скачать
Понятия: амплитудно-частотная, фазо-частотная характеристики - часть 10Скачать

Лекция 69. LC-фильтрСкачать

Урок 17. Как работает Интегрирующая и Дифференцирующая RC-цепь | Самое понятное объяснениеСкачать

Режекторный фильтрСкачать

Cетевой фильтр.Скачать

Коэффициент передачи. Фильтр нижних и верхних частот. Частотный метод анализа цепейСкачать