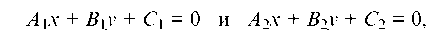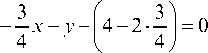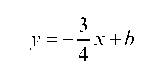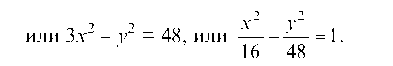Задать аналитически композицию двух осевых симметрий с осями заданными уравнениями

КОМПОЗИЦИИ ДВУХ ОСЕВЫХ СИММЕТРИЙ

ПРИ РАЗЛИЧНОМ РАСПОЛОЖЕНИИ ПРЯМЫХ

В ПЛОСКОСТИ ЛОБАЧЕВКОГО

Федорова Екатерина Михайловна,

магистр 2 года обуч.,

Пермский Государственный Педагогический Университет,

Изучаются осевые симметрии и их композиции при различном расположении прямых на плоскости Лобачевского, выясняются их свойства.
Геометрия плоскости Лобачевского строится на основе обобщения аксиоматики геометрии Д. Гильберта [1], [2], [3]. Иллюстрации полученных результатов проверяются на первой модели Пуанкаре плоскости Лобачевского [4], [5]. Так как основным движением является осевая симметрия, то рассмотрим ее свойства.

Точки и называются симметричными относительно заданной прямой , если эта прямая является серединным перпендикуляром к отрезку . Каждая точка прямой симметрична сама себе.

Определение 1. Преобразование плоскости, при котором каждая точка отображается на симметричную ей точку относительно данной прямой , называется осевой симметрией с осью и обозначается .

Так как результаты будем проверять на первой модели Пуанкаре, то была выполнена следующая интерпретация осевой симметрии на модели.

Рис. 1

1. если изображается евклидовым лучом, то получим евклидову осевую симметрию (рис. 1);
2. если изображается полуокружностью, то получим инверсию относительно полуокружности : (рис. 2).

Рассмотрим композиции двух осевых симметрий при различном расположении прямых.

Если даны две прямые и , такие, что:

1. , то результатом композиции будет тождественное преобразование:
2. , то композиция обладает следующими свойствами (рис. 3):

– неподвижная,

Вывод: и лежат на одной окружности с центром , результатом композиции будет поворот .

Рассмотрим необходимые определения понятий и их уже известные свойства, которые будем использовать для исследования данной композиции.

Определение 2. Поворотом плоскости около данной точки на заданный ориентированный угол величины называется преобразование плоскости, которое точку отображает на себя, а всякую другую точку отображает на такую точку , что и ориентированный угол имеет величину . Точка называется центром поворота, а величина углом поворота.

Рассмотрим некоторые свойства поворота:

1. Поворот плоскости является движением.
2. Поворот, как любое движение, отображает прямую на прямую, луч на луч, отрезок на отрезок.
3. Ориентированный угол между лучом и его образом при повороте равен углу поворота.

Поворот можно задать центром и углом или двумя прямыми и , пересекающимися в центре поворота, угол между которыми равен половине угла поворота [6], [7], [8].

Определение 3. Окружностью с центром и радиусом называется множество всех точек, удаленных от точки на расстояние .

Некоторые свойства окружности:

1. Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).
2. Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
3. Окружность симметрична относительно любой своей оси.
4. В каждой точке окружности существует касательная, которая перпендикулярна к оси, проходящей через точку касания.
5. Серединный перпендикуляр к любой хорде окружности является ее осью.

Докажем, что если два серединных перпендикуляра к сторонам треугольника пересекаются, то около такого треугольника можно описать окружность и только одну.

Пусть серединные перпендикуляры к сторонам соответственно (рис. 4) и пусть По свойствам серединного перпендикуляра и

Отсюда и Итак, точки и равноудалены от точки , т.е. лежат на одной окружности. Очевидно, эта окружность единственная.

Самостоятельно был доказан следующий факт. Пусть (рис. 5). Докажем, что найдется такая прямая , что и

Рассмотрим треугольник равнобедренный, проведем медиану

Медиана равнобедренного треугольника, опущенная на основание, одновременно является высотой и осью симметрии основания. Таким образом,

Докажем, что окружность симметрична относительно любой прямой, проходящей через ее центр.

Пусть даны окр и прямая и пусть . Рассмотрим (рис. 6). Очевидно, Если произвольная точка и то т.е. Так как то, обратно, каждая точка является прообразом некоторой точки . Итак,

Из доказанного выше вытекает второе определение окружности.

Определение 4. Окружностью называется множество точек, попарно симметричных относительно пучка пересекающихся прямых.

Прямые этого пучка называются осями окружности.

Известен тот факт, что не все свойства окружности евклидовой плоскости имеют место на плоскости Лобачевского. Например, теорема о том, что угол, вписанный в окружность и опирающийся на диаметр, является прямым углом, неверна на плоскости Лобачевского.

Пусть ее диаметр, (рис. 7). Треугольники и равнобедренные, следовательно, и .

Отсюда

Но

Следовательно, [1], [9].
Таким образом, были построены образы точек при повороте на модели Пуанкаре.

1. в некотором направлении.

Дадим определение параллельных прямых в плоскости Лобачевского.

Определение 5. Пусть и две ориентированные прямые. Прямая называется параллельнойаотносительноВв данном направлении, если

1. 
2. для любой точки любой внутренний луч из угла пересекает

Обозначение:

Известно, что данное определение не зависит от выбора точки Приведем доказательство этого факта.

Пусть и для некоторой точки любой внутренний луч из угла пересекает . Покажем, что это же будет верно для любой другой точки Для точки возможны случаи:

1. предшествует ;
2. следует за.

Рассмотрим эти случаи:

1. Если внутренний луч из то является либо внутренним лучом из либо либо внутренний луч из В первом случае пересекает по условию, во втором случае пересекает . В третьем случае пересекает отрезок (так как его концы лежат на разных сторонах этого угла), поэтому пересекает (рис. 10)
2. В этом случае Следовательно, любой внутренний луч из является внутренним лучом и для поэтому пересекает (рис. 11).

Рассмотрим следующее утверждение. Если и , то .

Для точки возможны два случая:

1. предшествует
2. 

следует за

Очевидно, .Докажем, что любой внутренний луч из пересекает . Предположим противное. Пусть в нашелся внутренний луч , не пересекающийся с

1. Пусть и (рис. 12). Очевидно, . Так как предшествует то Следовательно, внутренний луч для Тогда должен пересекать Но точки и лежат по разные стороны от . Прямые и не пересекают проходят через и соответственно, поэтому и лежат по разные стороны от . Следовательно, прямая не может пересекать . Получили противоречие. Отсюда следует, что любой внутренний луч из пересекает
2. Так как фигура лежит в то все точки луча лежат в Пусть Тогда внутренний луч для поэтому должен пересекать (рис. 13). Но Прямая не может пересекать иначе пересекла бы либо либо (по аксиоме Паша), что невозможно. Следовательно, Так как и прямая лежат по одну сторону от то и прямая лежат по разные стороны от прямой , т.е. Получили противоречие. Следовательно, и в этом случае внутренний луч из пересекает

Из доказанного выше следует, что в определении параллельных прямых слова «относительно точки» можно опустить.

Определение 6. Пусть и две ориентированные прямые. Прямая называется параллельнойав данном направлении, если

1. 
2. для любых точек любой внутренний луч из пересекает .

Обозначение [1], [8].

Рассмотрим необходимые определения понятий и их уже известные свойства, которые будем использовать для исследования данной композиции.

Определение 7. Орициклом называется множество точек плоскости попарно симметричных относительно прямых пучка параллельных в данном направлении прямых. Данный пучок называется определяющим пучком орицикла.

Известно, что если параллельна в данном направлении, то существует такая прямая что параллельна в том же направлении и

Проведем прямые параллельные в данном направлении (рис. 14). Прямые принадлежат одному пучку.

При этом прямая равного наклона для и прямая равного наклона для и

Следовательно, прямая равного наклона для и (по свойствам прямых равного наклона). Но это значит, что и симметричны относительно серединного перпендикуляра к и прямые и параллельны.

Следствие 1. Орицикл вполне задается определяющим пучком и одной точкой.

Следствие 2. Через любую точку плоскости для данного пучка проходит орицикл и только один.

Следствие 3. Орицикл симметричен относительно любой прямой определяющего пучка.

Пусть произвольная точка и Тогда

Прямые и принадлежат одному пучку параллельных прямых. Этот пучок определяет проходящий через точку орицикл . По свойствам орицикла точки и лежат на этом же орицикле. Итак, и лежат на одном орицикле, определяющему пучку которого принадлежат и .

Итак, результатом композиции будет движение, которое называют поворотом вокруг бесконечно удаленной точки (к которой сходятся прямые и ), или орициклическим поворотом. Если , то по свойствам осевой симметрии

(дуги ориентированные). По свойствам ориентированных длин

Отсюда следует, что все точки орицикла поворачивают по нему в одном направлении на одно и то же расстояние.

Орициклический поворот можно задать двумя прямыми определяющего пучка.

1. и сверхпараллельны.

Дадим определение сверхпараллельных прямых в плоскости Лобачевского.

Определение 8. Прямая называется сверхпараллельной а относительно точки В, если и не параллельна относительно точки ни в том, ни в другом направлении.

Чтобы перейти ко второму определению воспользуемся известным свойством сверхпараллельных прямых: если прямая параллельна прямой по данному направлению, то и прямая , в свою очередь, параллельна прямой по тому же направлению.

Определение 9. Прямая называется сверхпараллельной , если

и не параллельна ни в том, ни в другом направлении.

Обозначение

Рассмотрим необходимые определения понятий и их известные свойства, которые будем использовать для исследования данной композиции.

Пусть нетривиальный отрезок, Ориентируем прямую и проведем прямую (рис. 16), острый. Этот угол называется углом параллельности отрезка
Определение 10. Двупрямоугольником называется выпуклый четырехугольник с двумя прямыми углами, прилежащими к одной стороне. Если двупрямоугольник с прямыми углами и то сторона называется основанием, а стороны и боковыми сторонами.

Определение 11. Двупрямоугольник с равными боковыми сторонами называется четырехугольником Саккери.

Рассмотрим некоторые свойства двупрямоугольников.

Если четырехугольник Саккери с основанием , то и каждый из углов и острый.

Пусть серединный перпендикуляр к (рис. 17). Рассмотрим осевую симметрию с осью так как симметрия переводит полуплоскость с границей в себя и сохраняет углы. так как симметрия сохраняет расстояние. Отсюда следует, что серединный перпендикуляр к и (т.к. сумма углов выпуклого четырехугольника меньше ). Но так как , то каждый из этих углов острый.

Если у двупрямоугольника с основанием боковые стороны удовлетворяют условию то

Рассмотрим симметрию относительно серединного перпендикуляра в отрезку При этом точка перейдет в точку а точка в точку луча (рис 18). Так как и , то поэтому точка отрезка Четырехугольник является четырехугольником Саккери, поэтому Но а внешний угол треугольника Таким образом,

Основания четырехугольника Саккери являются сверхпараллельными прямыми. При этом прямая, соединяющая середины оснований, перпендикулярная им обоим.

Определение 12. Эквидистантой с базой и высотой называется множество всех возможных точек, лежащих в одной полуплоскости с границей и удаленных от на расстояние .

Известно, что эквидистанта симметрична относительно прямой, перпендикулярной ее базе.

Пусть эквидистанта с базой и высотой и любая точка . Если то Пусть Так как то где (рис. 19).

По свойствам осевой симметрии и эти лучи лежат в одной полуплоскости с границей . Так как симметрия сохраняет расстояние, то т.е. Итак, образ каждой точки лежит на . Так как то прообраз каждой точки лежит на . Итак,

Докажем, что если и две различные прямые, перпендикулярные то найдется такая прямая что

Пусть (рис. 20). При перпендикуляр, опущенный из точки на прямую , перейдет в перпендикуляр, опущенный из точки на прямую . Следовательно, и Аналогично,

Пусть серединный перпендикуляр к отрезку При (т.к. симметрия сохраняет перпендикулярность), (т.к. симметрия сохраняет принадлежность точек прямой и расстояние).

Из доказанного выше следует второе определение эквидистанты.

Определение 13. Эквидистантой называется множество всех точек, попарно симметричных относительно пучка прямых, перпендикулярных одной прямой. Этот пучок называется определяющим пучком.

Прямые и имеют общий перпендикуляр (рис. 21). Пусть произвольная точка и Тогда Прямые и задают пучок сверхпараллельных прямых, перпендикулярных . По свойствам эквидистанты точки лежат на одной эквидистанте с базой . Итак, точка получается из сдвигом по эквидистанте с базой Если то

Итак, результатом композиции будет движение, которое называют сдвигом вдоль прямой . Если то (аналогично предыдущему). Следовательно, все точки эквидистанты (или прямой ) сдвигаются вдоль нее в одном направлении на одно расстояние. Так как четырехугольники и есть четырехугольники Саккери с основанием то и . Итак, расстояние, на которое происходит сдвиг вдоль прямой , по прямой наименьшее и увеличивается при удалении точки от прямой Можно показать, что это увеличение неограниченно.

Известно, что сдвиг можно задать двумя прямыми определяющего пучка или прямой, вдоль которой происходит сдвиг, и двумя соответствующими точками [1], [3], [9], [10], [11].

1. Атанасян Л.С., Базылев В.Т. Геометрия. Ч II. М.: Просвещение, 1987.
2. Базылев В.Т., Дуничев К.И. Геометрия. Ч II. М.: Просвещение, 1975.
3. Ефимов Н.В. Высшая геометрия. М.: Наука, 1971.
4. Кутузов Б.В. Геометрия Лобачевского и элементы оснований геометрии. Учпедгиз, 1954.
5. Прасолов В.В. Геометрия Лобачевского. М.: МЦНМО, 2004.
6. Понарин Я.П. Элементарная геометрия. Планиметрия, преобразования плоскости. Ч I. М.: МЦНМО, 2004.
7. Гейдман Б. Композиция двух осевых симметрий // Квант. 1978. №2. С. 36-38.
8. Яглом И.М. Геометрические преобразования. Движения и преобразования подобия. Ч IМ.: Государственное издательство технико-теоретической литературы, 1955.
9. Андреева З.И., Шеремет Г.Г. Основания геометрии: элементы геометрии Лобачевского, Пермь: Перм. ун-т, 2007.
10. Атанасян Л.С., Гуревич Г.Б. Геометрия. Ч II. М.: Просвещение, 1976.
11. Атанасян Л.С. Геометрия Лобачевского. М.: Просвещение, 2001.

COMPOSITIONS OF TWO AXIS SYMMETRIES

UPON DIFFERENT DISPOSITION OF LINES

IN LOBACHEVSKY PLANE

Fedorova Ekaterina Mihajlovna,

magister of 2 year ed.,

Perm State Pedagogical University

Axis symmetries and their compositions upon all possible dispositions of lines in Lobachevsky plane were considered; their main properties were ascertained.

Изучаются осевые симметрии и их композиции при различном расположении прямых на плоскости Лобачевского, выясняются их свойства

17 12 2014
1 стр.

Тема Вводная лекция. Понятие композиции. Цели и задачи курса. Место курса основ композиции в специальных

01 10 2014
1 стр.

«Об одной композиции». Карова Альбина, 7 кл., Моу дод ддт с. Аргудан. Рук. Аталикова З. О

15 10 2014
1 стр.

Статья «Чудеса композиции» затрагивает вопросы, которые нам кажутся созвучными с нашей «книгой жалоб», относительно нарушений правил Кодекса судьями и организаторами конкурсов по к

09 10 2014
1 стр.

Композиция состоит из двух компонентов, которые соединяются перед подачей в шпур. Рекомендуемое время отверждения композиции при омоноличивании грунта 15-30 минут. Глубина шпура –

17 12 2014
1 стр.

Ыть жанровые композиции (изображения спортивных соревнований), портретные композиции (тематические, эпические, лирические портретные изображения имеющих отношение к спорту людей),

23 09 2014
1 стр.

Если пересадку осуществить на стадии поздней гаструлы, то у зародыша развиваются 2 осевых комплекса органов

15 09 2014
1 стр.

Переменная величина z называется функцией двух переменных величин x и y, если каждой паре допустимых значений x и y соответствует единственное значение z. Функция двух переменных о

Видео:Осевая симметрия. 6 класс.Скачать

1.3. Аналитическая геометрия. Аналитическая геометрия на плоскости

1.3.1. Аналитическая геометрия на плоскости

Если на плоскости произвольно взята декартова система координат, то всякое уравнение первой степени относительно текущих координат х и у

где А и B одновременно не равны нулю, определяет прямую в этой системе координат.

Верно и обратное утверждение: в декартовой системе координат всякая прямая может быть представлена уравнением первой степени вида (1.24).

Уравнение (1.24) называется общим уравнением прямой.

Углом наклона прямой к оси Ох называется наименьший угол j, на который нужно повернуть в положительном направлении ось абсцисс до ее совпадения с данной прямой. Направление любой прямой характеризуется ее угловым коэффициентом к, который определяется как тангенс угла наклона j этой прямой к оси Ох, т. е.

Исключение составляет только лишь прямая, перпендикулярная оси Ох, которая не имеет углового коэффициента.

Уравнение прямой, имеющей угловой коэффициент к и пересекающей ось Оу в точке, ордината которой равна b (начальная ордината), записывается в виде:

Частные случаи уравнения (1.24) приведены в следующей таблице.

Угловой коэффициент к прямой, заданной общим уравнением Ax + By + C= 0, находится как коэффициент при х в выражении у через х:

Угловой коэффициент к прямой, заданной двумя точками вычисляется по формуле

Уравнением прямой в отрезках называется уравнение вида:

где а и b — соответственно абсцисса и ордината точек пересечения прямой с осями Ох и Oy, т. е. длины отрезков, отсекаемых прямой на координатных осях, взятые с определенными знаками.

Уравнение прямой, проходящей через точкуИ имею

щей угловой коэффициент к, записывается в виде:

Пучком прямых называется совокупность прямых плоскости, проходящих через одну и ту же точку А — центр пучка. Уравнение (1.28) можно рассматривать как уравнение пучка прямых, поскольку любая прямая пучка может быть получены из уравнения (1) при соответствующем значении углового коэффициента к. Исключение составляет лишь одна прямая пучка, которая параллельна оси Oy — ее уравнение х = xA.

Уравнение прямой, проходящей через две данные точки имеет вид:

Если точки A и B определяют прямую, параллельную оси Или оси, то уравнение такой прямой за

писывается соответственно в виде:

Условия пересечения, параллельности или совпадения двух прямых, заданными своими общими уравнениями

приведены в следующей таблице.

Если известны угловые коэффициенты прямых, то ус

ловие параллельности этих прямых состоит в равенстве их угловых коэффициентов:

Условие перпендикулярности двух прямых, угловые коэффициенты которых соответственно равныСостоит в выполнении соотношения

т. е. угловые коэффициенты этих прямых обратны по абсолютной величине и противоположны по знаку.

Под углом между двумя прямыми понимается один из двух смежных углов, образованных при их пересечении. Тангенс угла j между двумя прямыми, угловые коэффициенты которых соответственно равны к1 и к2, вычисляется по формуле

причем знак «плюс» соответствует острому углу, а знак «минус» — тупому.

Уравнение окружности с центром в точке S^; b) и радиусом r имеем вид:

Это каноническое уравнение окружности (рис. 7).

Уравнение второй степени относительно текущих координат х и у является уравнением окружности тогда и только тогда, когда в этом уравнении коэффициенты при квадратах координат равны, а член с произведением координат отсутствует. Таким образом, это уравнение имеет вид:

В этом случае говорят, что окружность задана общим уравнением.

Для определения координат центра и радиуса окружности, заданной общим уравнением, надо с помощью тождественных преобразований уравнение (1.35) привести к виду (1.34).

Эллипс есть геометрическое место точек, сумма расстояний которых от двух фиксированных точек, называемых фокусами эллипса, есть величина постоянная (2а), большая, чем расстояние между фокусами (2с).

Простейшее уравнение эллипса получается, если расположить координатную систему следующим образом: за ось Оx принять прямую, проходящую через фокусы F1 и F2, а за ось Оу — перпен-

дикуляр к оси абсцисс в середине отрезка F1F2 (рис. 8). Тогда уравнение эллипса примет вид:

Точки А1 и А2, B1 и B2 пересечения эллипса с его осями симметрии (координатными осями) называются вершинами эллипса. Отрезки А1А2 = 2а и B1B2 = 2b называются осями эллипса, причем А1А2 — большой осью, а B1B2 — малой осью, так как а > b. Таким образом, параметры а и b, входящие в уравнение эллипса, равны его полуосям.

Эксцентриситетом эллипса называется отношение расстояния между фокусами к его большой оси, т. е.

Очевидно, что е а и уже большой осью будет отрезок B1B2 = 2b, а малой осью — отрезок А1А2 = 2а. Эксцентриситет такого эллипса вычисляется по формуле

Гиперболой называется геометрическое место точек, абсолютная величина разности расстояний которых от двух данных точек, называемых фокусами, есть величина постоянная (2а), меньшая, чем расстояние между фокусами (2с).

Простейшее уравнение гиперболы получается, если расположить координатную систему следующим образом: за ось Ох принять прямую, проходящую через фокусыА за ось Оу — перпендикуляр в середине отрезка(рис. 10). Тогда уравнение гиперболы примет вид:

Гипербола имеет две оси симметрии (координатные оси), с одной из которых (осью абсцисс) она пересекается в двух точках А1 и А2, называемых вершинами гиперболы. Отрезок.Называется действительной осью гиперболы, а отрезок— мнимой осью гиперболы.

Таким образом, параметры а и b, входящие в уравнение гиперболы, равны ее полуосям.

Эксцентриситетом гиперболы называется отношение расстояния между фокусами к ее действительной оси:

Ее асимптоты те же, что и у гиперболы (1.39).

Гиперболы (1.39) и (1.42) называются сопряженными. Гипербола называется равносторонней, если ее действительные и мнимые оси равны, т. е. а = b. Простейшее уравнение равносторонней гиперболы имеет вид:

Если мнимая ось гиперболы направлена по оси Ох и имеет длину 2а, а действительная ось длиной 2b направлена по оси Oy, то уравнение гиперболы (рис. 11) имеет вид:

Эксцентриситет такой гиперболы вычисляется по формуле

Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой параболы.

Величина р, равная расстоянию от фокуса до директрисы, называется параметром параболы; прямая, проходящая через фокус параболы перпендикулярно ее директрисе, называется осью, а точка пересечения параболы с ее осью — вершиной параболы.

Простейшее уравнение параболы получается, если координатная система расположена следующим образом: за одну из координатных осей берется ось параболы, а за другую — прямая, перпендикулярная оси параболы и проведенная посредине между фокусом и директрисой.

Тогда уравнение параболы примет вид:

определяет параболу, ось которой перпендикулярна оси абсцисс.

определяет параболу, ось которой перпендикулярна оси ординат.

Уравнения (1.48) и (1.49) приводятся к простейшему виду (1.44 — 1.47) путем тождественных преобразований с последующим параллельным переносом координатной системы.

Пример 1.16. Даны вершины А (2; 1), В (6; 3), C (4; 5) треугольника. Найти: 1) длину стороны АВ; 2) внутренний угол А в радианах с точностью до 0,01; 3) уравнение высоты, проведенной через вершину С; 4) уравнение медианы, проведенной через вершину С;

5) точку пересечения высот треугольника; 6) длину высоты, опущенной из вершины С; 7) систему линейных неравенств, определяющую внутреннюю область треугольника. Сделать чертеж.

Делаем чертеж (рис. 16).

1. Длину стороны АВ находим как расстояние между двумя точками А и В.

2. Для определения внутреннего угла А найдем уравнение прямой AC:

отсюда 2х — у — 3 = 0 или у = 2х — 3 и угловой коэффициент прямой AC равен: kAC = 2; далее находим уравнение прямой АВ:

Находим угол А отсюда

3. Уравнение высоты, проведенной через вершину C, ищем в виде у — yC = kCD (x — xC) и так как CD А прямой АВ, то

4. Для определения уравнения медианы CM находим координаты точки M, которая делит прямую АВ пополам

Уравнение прямой CM ищем в виде:

а это означает, что уравнение медианы имеет вид х = 4, т. е. прямая CM L Ох.

5. Точку пересечения высот треугольника найдем как точку К пересечения высот CD и BK.

Находим уравнение высоты ВК:

Решаем систему уравнений, описывающих прямые CD и BK:

Тогдат. е. координаты точ

ки К будут:

6. Для нахождения длины высоты CD запишем нормальное уравнение прямой АВ:

7. Находим систему линейных неравенств, определяющих внутреннюю область треугольника.

Найдем уравнение прямой BC:

Итак:

Берем любую точку, лежащую внутри треугольника, например, (4; 3) и подставляем ее координаты в левую часть уравнений прямых:

следовательно, система неравенств имеет вид:

Пример 1.17. Составить уравнение прямой I, проходящей через точку А (2; -4) и отстоящей от начала координат на расстоянии, равном 2 единицам.

Решение. Пусть уравнение искомой прямой имеет вид:

Для определения углового коэффициента к этой прямой воспользуемся тем, что она отстоит от начала координат на расстоянии, равном 2 единицам. Найдем это расстояние непосредственно. Уравнение перпендикуляра, опущенного из начала координат на прямую, имеет вид илиРешив совместно уравнения этих двух прямых

С другой стороны, по условию OC = 2. Таким образом, получаем уравнение для нахождения углового коэффициента к искомой прямой I:

получим координаты точки C их пересечения:

Отсюда находим расстояние от начала координат до прямой I:

В заключение отметим, что отыскивая уравнение прямой I в виде у — yA = k(x — Xa), мы предполагали тем самым, что эта прямая не параллельна оси ординат. Но очевидно, что прямая х = 2 (параллельная оси Оу) также удовлетворяет условию задачи, так как она проходит через точку А (2; -4) и отстоит от начала координат на расстоянии, равном 2 единицам (рис. 17).

Пример 1.18. Составить уравнения прямых, параллельных прямой 3х + 4у — 1 = 0 (I) и отстоящих от нее на расстоянии равном 1.

Решение. Уравнение каждой из прямых будем искать в виде Так как искомая прямая параллельна прямой I, то ее

угловой коэффициентИ, следовательно, ее уравнение при

нимает вид:

Для отыскания параметра b воспользуемся тем, что расстояние от любой точки прямой I, например, от точки А (3; -2) до прямой (*) согласно условию равно 1. Но это расстояние может быть вычислено и непосредственно. Запишем для этого

уравнение прямой h, проведенной из точки А перпендикулярно прямой I:

Решив, далее, совместно уравнения прямых h и I найдем координаты точки В их пересечения:

Тогда искомое расстояние равно длине отрезка АВ:

Приравнивая это выражение единице, получим уравнение относительно b:

Решения этого уравнения таковы:. Подставляя полученные значения b в уравнение (*), запишем уравнения искомых прямых:

Пример 1.19. Составить уравнение линии, расстояние каждой точки которой от точки F (8; 0) вдвое больше, чем от прямой х — 2 = 0. Сделать чертеж.

Пусть М(х; у) — текущая точка линии. По условию задачи MF = 2MN.

Возводя в квадрат и раскрывая скобки, получим

Это есть каноническое уравнение гиперболы (рис. 18).

Пример 1.20. Составить уравнение линии, каждая точка которой равноудалена от точки F (0; — 4) и от прямой у + 2 = 0. Сделать чертеж.

Если M(x; у) есть текущая точка линии, то по условию задачи MF = MN или

Подставляя координаты точек

И возводя в квадрат, после преобразований

Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

Композиции перемещений плоскости

Некоторые наиболее сложные задачи на построение решаются методом последовательного применения нескольких перемещений плоскости, которое называется композицией перемещений, поэтому мы в этом параграфе рассмотрим некоторые сведения, относящиеся к вопросу о композиции перемещений.

Определение 4.11. Композицией двух преобразований называется результат последовательного выполнения этих преобразований.

Определив композиции перемещений плоскости, мы можем рассмотреть еще одно перемещение плоскости — скользящая симметрия.

Видео:101 Композиция двух осевых симметрийСкачать

Скользящая симметрия

Определение 4.12. Скользящей, или переносной, симметрией называется композиция осевой симметрии и параллельного переноса, вектор которого параллелен оси симметрии.

Скользящую симметрию с осью d и вектором а обозначают так: S$, или сокращенно d₅. Параллельный перенос на нулевой вектор есть тождественное преобразование, поэтому, если а = б, то S° = Sj. Осевая симметрия — частный случай скользящей симметрии.

Рассмотрим свойства скользящей симметрии.

• 1. Композиция осевой симметрии и параллельного переноса обладает переместительным свойством.
• 2. Скользящая симметрия неподвижных точек не имеет.
• 3. Ось d — единственная неподвижная прямая скользящей симметрии.
• 4. Скользящая симметрия — перемещение II рода.

Укажем некоторые наиболее важные свойства композиции перемещений плоскости.

Теорема 4.3. Всякое перемещение плоскости есть композиция не более трех осевых симметрий.

Теорема 4.4. Композиция двух осевых симметрий, оси которых параллельны, есть параллельный перенос. Вектор переноса перпендикулярен осям и направлен от первой оси ко второй, а его модуль равен удвоенному расстоянию между осями.

Теорема 4.5. Композиция двух осевых симметрий, оси которых пересекаются, есть поворот вокруг точки пересечения осей. Угол поворота равен удвоенному углу от первой оси до второй.

Теорема 4.6. Композиция трех осевых симметрий есть осевая симметрия тогда и только тогда, когда оси данных симметрий имеют единственную точку или параллельны между собой.

Теорема 4.7. Композиция трех осевых симметрий, оси которых не параллельны и не имеют общей точки, есть скользящая симметрия.

Теорема 4.8 (Шаля). Всякое перемещение плоскости —либо поворот, либо параллельный перенос, либо осевая симметрия, либо скользящая симметрия.

Теорема 4.9. Композиция В^А_а двух поворотов А_а и Вр есть или поворот С_а+р, если а + (3 2я.

Теорема 4.10. Два перемещения обладают переместительным свойством тогда и только тогда, когда одно перемещение посредством другого преобразуется в себя.

Теорема 4.11. На плоскости переместительным свойством обладают:

• 1) две осевые симметрии с перпендикулярными осями;
• 2) осевая и центральная симметрии, если ось проходит через центр;
• 3) осевая симметрия и параллельный перенос, если вектор параллелен оси;
• 4) осевая и скользящая симметрии, если их оси совпадают;
• 5) два параллельных переноса;
• 6) параллельный перенос и скользящая симметрия, если вектор параллелен оси;
• 7) два поворота с общим центром(в частности, центральная симметрия и поворот с общим центром).
• 8) две скользящие симметрии с общей осью.

Приведем таблицу (табл. 4.2), которая содержит ответ на вопрос, что представляет собой композиция тех или иных перемещений плоскости.

🔍 Видео

ОГЭ по математике. Задание 17. Центральная и осевая симметрияСкачать

6 класс, 26 урок, СимметрияСкачать

Ось симметрииСкачать

11 класс, 10 урок, Осевая симметрияСкачать

Центральная симметрия. 6 класс.Скачать

Симметрия.Скачать

Осевая и центральная симметрия, 6 классСкачать

СИММЕТРИЯ | осевая симметрия | центральная симметрияСкачать

Геометрия 8 класс (Урок№7 - Осевая и центральная симметрия.)Скачать

48. Осевая и центральная симметрииСкачать

Осевая и центральная симметрия.Скачать

11 класс, 9 урок, Центральная симметрияСкачать

Технология 2 класс (Урок№3 - Что такое симметрия?)Скачать

Математика 6 Осевая симметрияСкачать

Осевая и центральная симметрии. 6 класс.Скачать

Симметрия относительно прямой (осевая симметрия). Пример 2Скачать

Осевая симметрия, 6 классСкачать