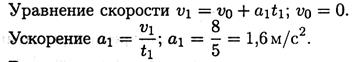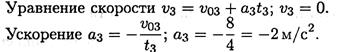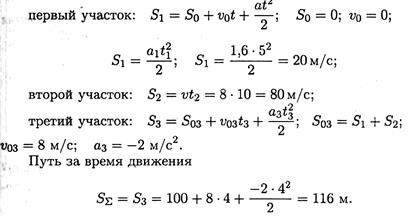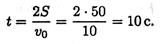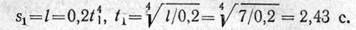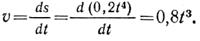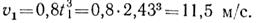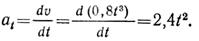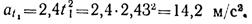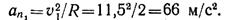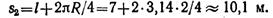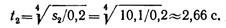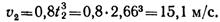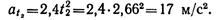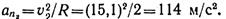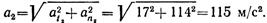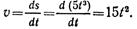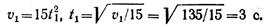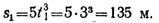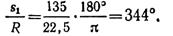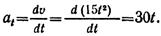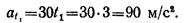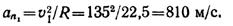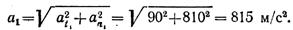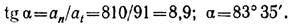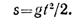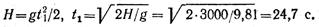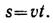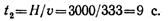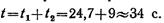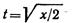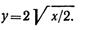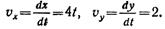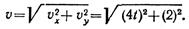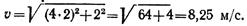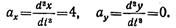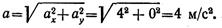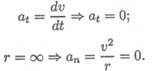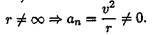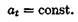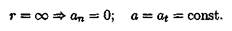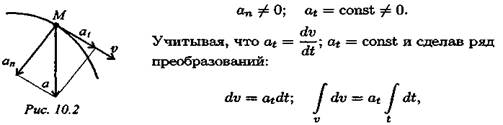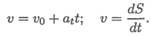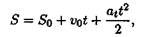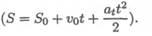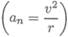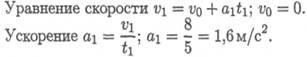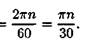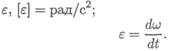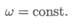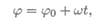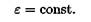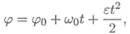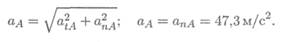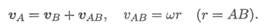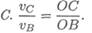Задано уравнение s 10 20t 5t2 определить начальную скорость пройденную до начала отсчета

Пример 1. По заданному закону движения S =10 + 20t — 5t 2 ([S] = м; [t] = с) определить вид движения, начальную скорость и касательное ускорение точки, время до остановки.

(Рекомендуется обойтись без расчетов, использовать метод срав­нения заданного уравнения с уравнениями различных видов движе­ний в общем виде.)

Решение

1. Вид движения: равнопеременное

2. При сравнении уравнений очевидно, что

• начальный путь, пройденный до начала отсчета – 10 м;
• начальная скорость 20 м/с;
• постоянное касательное ускорение a_t/2 = 5 м/с ; a_t= — 10 м/с .
• ускорение отрицательное, следовательно, движение замедлен­ное (равнозамедленное), ускорение направлено в сторону, противо­положную направлению скорости движения.

3. Можно определить время, при котором скорость точки будет равна нулю:

v = S’ = 20 — 2 • 5t; v = 20 – 10t = 0; t = 20/10 = 2 c.

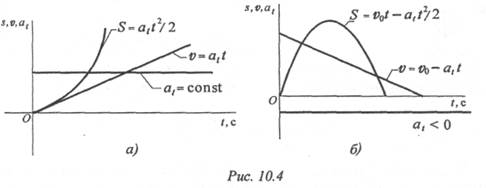
Примечание. Если при равнопеременном движении скорость растет, значит, ускорение — положительная величина, гра­фик пути — вогнутая парабола. При торможении скорость падает, ускорение (замедление) — отрицательная величина, график пути — выпуклая парабола (рис. 10.4).

Пример 2. Точка движется по желобу из точки А в точку D (рис. 10.5).

Как изменятся касательное и нормальное ускорения при прохождении точки через В и С?

Скорость движения считать постоянной. Радиус участка АВ = 10 м, радиус участка ВС= 5 м.

Дата добавления: 2015-09-07 ; просмотров: 2106 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Примеры решения задач

Пример 1. По заданному закону движения S =10 + 20t — 5t 2 ([S] = м; [t] = с) определить вид движения, начальную скорость и касательное ускорение точки, время до остановки.

(Рекомендуется обойтись без расчетов, использовать метод срав­нения заданного уравнения с уравнениями различных видов движе­ний в общем виде.)

Решение

1. Вид движения: равнопеременное

2. При сравнении уравнений очевидно, что

• начальный путь, пройденный до начала отсчета – 10 м;
• начальная скорость 20 м/с;
• постоянное касательное ускорение a_t/2 = 5 м/с ; a_t= — 10 м/с .
• ускорение отрицательное, следовательно, движение замедлен­ное (равнозамедленное), ускорение направлено в сторону, противо­положную направлению скорости движения.

3. Можно определить время, при котором скорость точки будет равна нулю:

v = S’ = 20 — 2 • 5t; v = 20 – 10t = 0; t = 20/10 = 2 c.

Примечание. Если при равнопеременном движении скорость растет, значит, ускорение — положительная величина, гра­фик пути — вогнутая парабола. При торможении скорость падает, ускорение (замедление) — отрицательная величина, график пути — выпуклая парабола (рис. 10.4).

Пример 2. Точка движется по желобу из точки А в точку D (рис. 10.5).

Как изменятся касательное и нормальное ускорения при прохождении точки через В и С?

Скорость движения считать постоянной. Радиус участка АВ = 10 м, радиус участка ВС= 5 м.

Решение

1. Рассмотрим участок АВ. Касательное ускорение равно нулю (v = const).

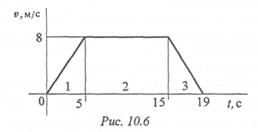
Нормальное ускорение (а_п = v 2 /r) при переходе через точку В уве­личивается в 2 раза, оно меняет направление, т. к. центр дуги АВ не совпадает с центром дуги ВС.

2. На участке ВС:

— касательное ускорение равно нулю: a_t = 0;

— нормальное ускорение при переходе через точку С меняется: до точки С движение вращательное, после точки С движение стано­вится прямолинейным, нормальное напряжение на прямолинейном участке равно нулю.

3. На участке CD полное ускорение равно нулю.

Пример 3. По заданному графику скорости найти путь, прой­денный за время движения (рис. 10.6).

Решение

1. По графику следует рассмотреть три участка движения. Первый участок — разгон из состояния покоя (равноускоренное движение).

Второй участок — равномерное движение: v = 8 м/с; a₂ = 0.

Третий участок — торможение до остановки (равнозамедленное движение).

2. Путь, пройденный за время движения, будет равен:

Пример 4. Тело, имевшее начальную скорость 36 км/ч, про­шло 50 м до остановки. Считая движение равнозамедленным, опре­делить время торможения.

Решение

1. Записываем уравнение скорости для равнозамедленного дви­жения:

Определяем начальную скорость в м/с: v_о = 36*1000/3600 = 10 м/с.

Выразим ускорение (замедление) из уравнения скорости: a = — v₀/t

2. Записываем уравнение пути: S = v_ot/2 + at 2 /2. После подстановки получим: S = v_ot/2

3. Определяем время до полной остановки (время торможения):

Пример 5. Точка движется прямолинейно согласно уравнению s = 20t – 5t 2 (s — м, t — с). Построить графики расстояний, скорости и ускорения для первых 4 с движения. Определить путь, пройденный точкой за 4 с, и описать движение точки.

Решение

1. Точка движется прямолинейно по уравнению s = 20t – 5t 2 следовательно, скорость точки u = ds/d/t = 20 — 10t и ускорение a = a_t = dv/dt = —10 м/с 2 . Значит, движение точки равнопеременное (a = a_t = —10 м/c 2 = const) с начальной скоростью v₀ = 20 м/с.

2. Составим зависимость числовых значений s и v для первых 4 с движения

3. По приведенным числовым значениям построим графики расстояний (рис. а), скорости (рис. б) и ускорения (рис. в), выбрав мас­штабы для изображения по осям ординат расстояний s, скорости v и ускорения а, а также одинаковый для всех графиков масштаб времени по оси абсцисс. Напри­мер, если расстояние s = 5 м изображать на графике длиной отрезка l_s = 10 мм, то 5м = μ_s*10мм, где коэффициент пропорциональности μ_s и есть масштаб по оси Os : μ_s = 5/10 = 0,5 м/мм (0,5 м в 1 мм); если модуль скорости v = 10 м/с изобра­жать на графике длиной l_v =10 мм, то 10 м/c = μ_v * 10 мм и масштаб по оси Ov μ_v = 1 м/(с-мм) (1 м/с в 1 мм); если модуль ускорения а = 10 м/с 2 изображать отрезком l_a = 10 мм, то, аналогично предыдущему, масштаб по оси Оа μ_a = 1 м/(с 2 -мм) (1 м/с 2 в 1 мм); и наконец, изображая промежуток време­ни Δt = 1 с отрезком μ_t = 10 мм, получим на всех графиках масштаб по осям Ot μ_t = 0,1 с/мм (0,1 с в 1 мм).

4. Из рассмотрения графиков следует, что в течение времени от 0 до 2 с точка движется равнозамедленно (скорость v и ускорение в течение этого промежутка времени имеют разные знаки, значит, их векторы направлены в противоположные стороны); в период времени от 2 до 4 с точка движется равноускоренно (скорость v и ускорение имеют одинаковые знаки, т. е. их векторы направлены в одну сто­рону).

За 4 с точка прошла путь s_o_₄ = 40 м. На­чав движение со скоростью v₀ = 20 м/с, точка по прямой прошла 20 м, а затем вернулась в исходное положение, имея ту же скорость, но направленную в противоположную сторону.

Если условно принять ускорение свободно­го падения g = 10 мс 2 и пренебречь сопротивле­нием воздуха, то можно сказать, что графики описывают движение точки, брошенной верти­кально вверх со скоростью а₀ = 20 м/с.

Пример 6. Точка движется по траектории, изображенной на рис. 1.44, а, согласно уравнению s = 0,2t 4 (s — в метрах, t — в секундах). Определить скорость и ускорение точки в положениях 1 и 2.

Решение

Время, необходимое для перемещения точки из положения 0 (начала отсчета) в положение 1, опреде­лим из уравнения движения, подставив частные значения расстояния и времени:

Уравнение изменения скорости

Скорость точки в положении 1

Уравнение изменения касательного ускорения

Касательное ускорение точ­ки в положении 1

Нормальное ускорение точки на прямолинейном участке траектории равно нулю. Ско­рость и ускорение точки в конце этого участка траекто­рии показаны на рис.1.44, б.

Определим скорость и уско­рение точки в начале криво­линейного участка траектории. Очевидно, что v₁ = 11,5 м/с, а_t1 = 14,2 м/с 2 .

Нормальное ускорение точки в начале криволинейного участка

Скорость и ускорение в начале криволинейного участ­ка показаны на рис. 1.44, в (векторы a_t1 и a_a1 изобра­жены без соблюдения масштаба).

Положение 2 движущейся точки определяется прой­денным путем, состоящим из прямолинейного участка 0 — 1 и дуги окружности 1 — 2, соответствующей цент­ральному углу 90°:

Время, необходимое для перемещения точки из поло­жения 0 в положение2,

Скорость точки в положении 2

Касательное ускорение точки в положении 2

Нормальное ускорение точки в положении 2

Ускорение точки в положении 2

Скорость и ускорения точки в положении 2 показаны на рис. 1.44, в (векторы at„ и а_Пг изображены без соблюде­ния масштаба).

Пример 7. Точка движется по заданной траекто­рии (рис. 1.45, а) согласно уравнению s = 5t 3 (s — в мет­рах, t — в секундах). Определить ускорение точки и угол α между ускорением и скоростью в момент t₁, когда скорость точки v₁ = 135 м/с.

Решение

Уравнение изменения скорости

Время t₁ определим из уравнения изменения скорости, подставив частные значения скорости и времени:

Определим положение точки на траектории в момент 3 с:

Дуга окружности длиной 135 м соответствует цент­ральному углу

Уравнение изменения касательного ускорения

Касательное ускорение точки в момент t_t

Нормальное ускорение точки в момент t_t

Ускорение точки в момент t_x

Скорость и ускорение точки в момент времени t₁ по­казаны на рис. 1.45, б.

Как видно из рис. 1.45, б

Пример 8. В шахту глубиной H = 3000 м с по­верхности земли без начальной скорости брошен предмет. Определить, через сколько секунд звук, возникающий в момент удара предмета о дно шахты, достигнет поверх­ности земли. Скорость звука 333 м/с.

Решение

Уравнение движения свободно падающего тела

Время, необходимое для перемещения предмета от поверхности земли до дна шахты, определим из уравне­ния движения:

Звук распространялся с постоянной скоростью 333 м/с. Уравнение распространения звука

Время достижения звуком поверхности земли

Тогда время с момента начала движения предмета до момента достижения звуком поверхности земли

Пример 9. По заданным уравнениям движения точки x = 2t 2 , y = 2t (x и у — в метрах, t — в секундах) найти уравнение траектории, а также скорость и уско­рение точки в момент времени t = 2 с.

Решение

Для определения траектории точки нужно из уравнений движения исключить параметр t — время.

Выразим t через х из первого уравнения:

и подставим это значение во второе уравнение:

Траекторией точки является парабола, симметричная относительно оси х.

Чтобы найти скорость точки, нужно определить ее составляющие по координатным осям

Находим скорость точки

При t = 2 с получаем

Находим составляющие ускорения точки

Контрольные вопросы и задания

1. Запишите формулу ускорения при прямолинейном движении.

2. Запишите формулу ускорения (полного) при криволинейном движении.

3. Тело скатывается по желобу (рис. 10.7). Какие параметры движения меняются при переходе через точку В и почему?

4. Параметры движения не меняются.

4. По заданному уравнению движения точки S = 25 + 1,5t + 6t 2 определите вид движения и без расчетов, используя законы движе­ния точки, ответьте, чему равны начальная скорость и ускорение.

5. По заданному уравнению движения точки S = 22t — 4t 2 постройте графики скорости и касательного ускорения.

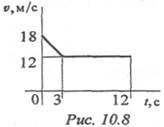
6. По графику скоростей точки определите путь, пройденный за время движения (рис. 10.8).

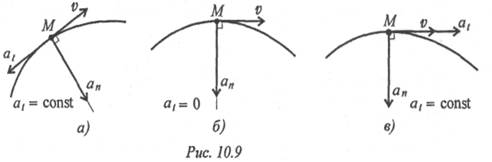
7. Точка движется по дуге. Охарактеризуй движение точки (рис. 10.9).

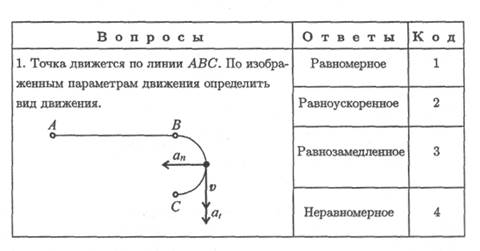
8. Ответьте на вопросы тестового задания.

Темы 1.7, 1.8. Кинематика. Кинематика точки

.

ЛЕКЦИЯ 11

Дата добавления: 2017-09-01 ; просмотров: 10659 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Решение графических задач на равномерное движениеСкачать

Уравнение движения тела дано в виде х = 4 — 3t. Определить начальную координату тела, скорость движения и перемещение тела за 2 секунды

Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Ваш ответ

Видео:Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

решение вопроса

Видео:Задача из ЕГЭ по физике │Анализ графика #1Скачать

Похожие вопросы

• Все категории
• экономические 43,419
• гуманитарные 33,633
• юридические 17,906
• школьный раздел 608,162
• разное 16,857

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Задано уравнение s 10 20t 5t2 определить начальную скорость пройденную до начала отсчета

параметров движений

Равномерное движение

Равномерное движение — это движение с постоянной скоро­стью:

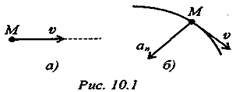
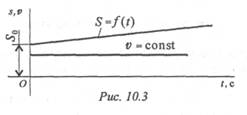
Для прямолинейного равномерного движения (рис. 10.1а)

Полное ускорение движения точ­ки равно нулю: а = 0.

При криволинейном равномер­ном движении (рис. 10.16)

Полное ускорение равно нормальному ускорению: а = а_п.

Уравнение (закон) движения точки при равномерном движении можно получить, проделав ряд несложных операций.

Так как v = const, закон равномерного движения в общем виде является уравнением прямой: S = So + vt , где So — путь, пройденный до начала отсчета.

Равнопеременное движение

Равнопеременное движение — это движение с постоянным ка­сательным ускорением:

Для прямолинейного равнопеременного движения

Полное ускорение равно касательному ускорению. Криволинейное равнопеременное движение (рис. 10.2):

получим значение скорости при равнопеременном движении

После интегрирования будем иметь закон равнопеременного движения в общем виде, представляющий уравнение параболы:

где v0 — начальная скорость движения;

S0 — путь, пройденный до начала отсчета;

a t — постоянное касательное ускорение.

Неравномерное движение

При неравномерном движении численные значения скорости и ускорения меняются.

Уравнение неравномерного движения в общем виде представля­ет собой уравнение третьей S = f ( t 3 ) и выше степени.

Тема 1.8. Кинематика точки 73

Кинематические графики

Кинематические графики — это графики изменения пути, ско­рости и ускорений в зависимости от времени.

Равномерное движение (рис. 10.3)

Равнопеременное движение (рис. 10.4)

Примеры решения задач

Пример 1. По заданному закону движения S = 10 + 20t — 5t 2 ([ S ] = м; [ t ] = с) определить вид движения, начальную скорость и касательное ускорение точки, время до остановки.

(Рекомендуется обойтись без расчетов, использовать метод сравнения заданного уравнения с уравнениями различных видов дви­жений в общем виде.)

Решение

1. Вид движения: равнопеременное

2. При сравнении уравнений очевидно, что

— начальный путь, пройденный до начала отсчета 10 м;

— начальная скорость 20 м/с;

— постоянное касательное ускорение — = — 5 м/с² ; at =—10 м/с² .

— ускорение отрицательное, следовательно, движение замедлен­ное (равнозамедленное), ускорение направлено в сторону, противо­положную направлению скорости движения.

3. Можно определить время, при котором скорость точки будет равна нулю:

v = S ´ = 20 — 2 • 5t; v = 20 – 10t; v = 0; t = — = 2 с .

Примечание. Если при равнопеременном движении скорость растет, значит, ускорение — положительная величина, гра­фик пути — вогнутая парабола. При торможении скорость падает, ускорение (замедление) — отрицательная величина, график пути — выпуклая парабола (рис. 10.4).

Пример 2. Точка движется по желобу из точки А в точку D (рис. 10.5).

Как изменятся касательное и нормальное ускорения при прохождении точки через В и С?

Скорость движения считать постоянной. Радиус участка АВ = 10 м, радиус участка ВС= 5м.

Решение

1. Рассмотрим участок АВ. Касательное ускорение равно нулю (г> = const).

Нормальное ускорение при переходе через точку В увеличивается в 2 раза, оно меняет направление, т. к. центр дуги АВ не совпадает с центром дуги ВС.

2. На участке ВС:

— касательное ускорение равно нулю: at = 0;

— нормальное ускорение при переходе через точку С меняется: до точки С движение вращательное, после точки С движение стано­вится прямолинейным, нормальное напряжение на прямолинейном участке равно нулю.

3. На участке CD полное ускорение равно нулю.

Тема 1.8. Кинематика точки 75

Пример 3. По заданному графику скорости найти путь, прой­денный за время движения (рис. 10.6).

Решение

1. По графику следует рассмотреть три участка движения.

Первый участок — разгон из состояния покоя (равноускоренное движение).

Второй участок — равномерное движение: v = 8 м/с; а2 = 0.

Третий участок — торможение до остановки (равнозамедленное движение).

Пример 4. Тело, имевшее начальную скорость 36 км/ч, про­шло 50 м до остановки. Считая движение равнозамедленным, опре­делить время торможения.

Решение

1. Записываем уравнение скорости для равнозамедленного дви­жения:

Контрольные вопросы и задания

1. Запишите формулу ускорения при прямолинейном движении.

2. Запишите формулу ускорения (полного) при криволинейном движении.

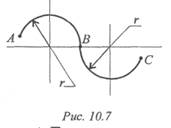
3. Тело скатывается по желобу (рис. 10.7). Какие параметры движения меняются при переходе через точку В и почему?

4. Параметры движения не меняются.

4. По заданному уравнению движения точки S = 25 + 1,5t + 6t 2 определите вид движения и без расчетов, используя законы движе­ния точки, ответьте, чему равны начальная скорость и ускорение.

Тема 1.8. Кинематика точки 77

5. По заданному уравнению движения точки S = 22t — 4t 2 по­стройте графики скорости и касательного ускорения.

6. По графику скоростей точки опреде­лите путь, пройденный за время движения (рис. 10.8).

7. Точка движется по дуге. Охарактеризуйте движение точки (рис. 10.9).

8. Ответьте на вопросы тестового задания.

Темы 1.7, 1.8. Кинематика.

Кинематика точки

Тема 1.9. Простейшие движения твердого тела 79

Тема 1.9. Простейшие движения твердого тела

Иметь представление о поступательном движении, его осо­бенностях и параметрах, о вращательном движении тела и его параметрах.

Знать формулы для определения параметров поступательного и вращательного движений тела.

Уметь определять кинематические параметры тела при по­ступательном и вращательном движениях, определять параме­тры любой точки тела.

Поступательное движение

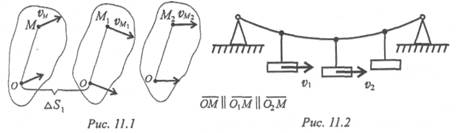
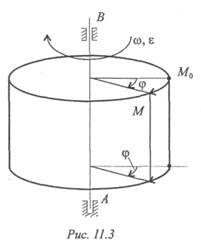
Поступательным называют такое движение твердого тела, при котором всякая прямая линия на теле при движении остается парал­лельной своему начальному положению (рис. 11.1, 11.2).

При поступательном движении все точки тела движутся одина­ково: скорости и ускорения в каждый момент одинаковы. Поэтому для описания движения тела можно рассматривать движение одной его точки, обычно центра масс.

Поступательное движение может быть прямолинейным и кри­волинейным.

Вращательное движение

При вращательном движении все точки тела описывают окруж­ности вокруг общей неподвижной оси.

Неподвижная ось, вокруг которой вращаются все точки тела, называется осью вращения.

При этом каждая точка движется по окружности, радиус кото­рой равен расстоянию точки до оси вращения. Точки на оси враще­ния не перемещаются.

Для описания вращательного движения тела вокруг непо­движной оси можно использовать только угловые параметры (рис, 11.3):

φ— угол поворота тела, [φ] = рад;

ω — угловая скорость, определяет изменение угла поворота в единицу времени, [ω] = рад/с.

Для определения положения тела в любой момент времени ис­пользуется уравнение φ = f ( t ).

Следовательно, для определе­ния угловой скорости можно пользоваться

Иногда для оценки быстро­ты вращения используют угловую частоту вращения п, которая оце­нивается в оборотах в минуту.

Угловая скорость и частота вращения физически близкие ве­личины ω

Изменение угловой скорости во времени определяется угловым ускорением

Частные случаи вращательного движения

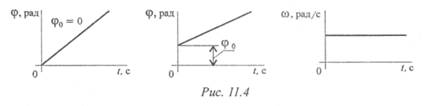
Равномерное вращение (угловая скорость постоянна):

Уравнение (закон) равномерного вращения в данном случае име­ет вид:

Тема 1.9. Простейшие движения твердого тела 81

где φ0 — угол поворота до начала отсчета.

Кинематические графики для этого вида движения изображены на рис. 11.4.

Равнопеременное вращение (угловое ускорение постоянно):

Уравнение (закон) равнопеременного вращения

где ω0 — начальная угловая скорость.

Угловое ускорение при ускоренном движении — величина поло­жительная; угловая скорость будет все время возрастать.

Угловое ускорение при замедленном движении — величина от­рицательная; угловая скорость убывает.

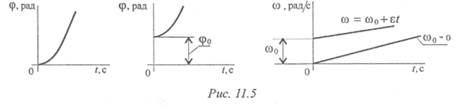
Для данного движения кинематические графики представлены, на рис. 11.5.

Скорости и ускорения точек вращающегося тела

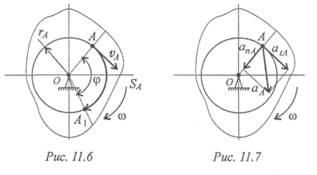
Тело вращается вокруг точки О. Определим параметры дви­жения точки А, расположенной на расстоянии rA от оси вращения (рис. 11.6, 11.7).

Путь точки A : S a = φ r A .

Линейная скорость точки A : v A = ω r A .

Ускорения точки A : at A = ε r A — касательное; а_п А = ω 2 r A — нормальное, где r A— радиус окружности, траектории точки А.

Примеры решения задач

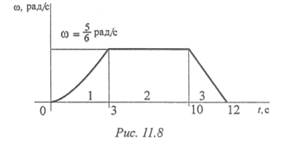
Пример 1. По заданному графику угловой скорости (рис. 11.8) определить вид вращательного движения.

Решение

1. Участок 1 — неравномерное ускоренное движение,ω = φ´; ε = ω‘.

2. Участок 2 — скорость постоянна — движение равномерное, ω = const.

3. Участок 3 — скорость убывает равномерно — равнозамедленное движение, ε = ω‘ 2 r A ; а_{п A} = (12,56) 2 • 0,3 = 47,3м/с 2 .

5. Полное ускорение точек на ободе колеса

Контрольные вопросы и задания

1. Какими кинематическими параметрами характеризуется по­ступательное движение и почему?

2. Запишите уравнение равномерного поступательного движе­ния твердого тела.

3. Запишите уравнение равнопеременного поступательного дви­жения твердого тела.

4. Запишите уравнения равномерного и равнопеременного вра­щательного движений твердого тела.

5. Задано уравнение движения тела S = f ( t ). Как определяют скорость и ускорение?

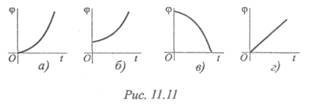
6. Для заданного закона (уравнения) движения φ = 6,28 + 12 t + +3t 2 выберите соответствующий кинематический график движения (рис. 11.11).

7. Для движения, закон которого задан в вопросе б, определите
угловое ускорение в момент t = 5 с.

Тема 1.10. Сложное движение точки.

Сложное движение твердого тела

Иметь представление о системах координат, об абсолютном, относительном и переносном движениях.

Знать разложение сложного движения на относительное и переносное, теорему сложения скоростей.

Знать разложение плоскопараллельного движения на посту­пательное и вращательное, способы определения мгновенного цен­тра скоростей.

Основные определения

Сложным движением считают движение, которое можно разло­жить на несколько простых. Простыми движениями считают посту­пательное и вращательное.

Для рассмотрения сложного движения точки выбирают две си­стемы отсчета: подвижную и неподвижную.

Движение точки (тела) относительно неподвижной системы от­счета называют сложным, или абсолютным.

Подвижную систему отсчета обычно связывают с движущимся телом. Движение подвижной системы отсчета относительно непо­движной называют переносным.

Движение материальной точки (тела) по отношению к подвиж­ной системе называют относительным.

Примером может служить движение человека по эскалатору ме­тро. Движение эскалатора — переносное движение, движение чело­века вниз или вверх по эскалатору — относительное, а движение по отношению к неподвижным стенам станции — сложное (абсолют­ное) движение.

При решении задач используют теорему о сложении скоростей:

При сложном движении точки абсолютная скорость в ка­ждый момент времени равна геометрической сумме переносной ( v_e ) и относительной ( v_r ) скоростей:

а — угол между векторами v_е и v_r

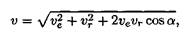
Тема 1.10. Сложное движение точки 87

Плоскопараллельное движение твердого тела

Плоскопараллельным, или плоским, называется такое движение твердого тела, при котором все точки тела перемещаются парал­лельно некоторой неподвижной в рассматриваемой системе отсчета плоскости.

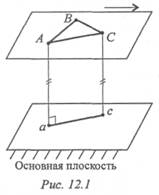
Плоскопараллельное движение мож­но изучать, рассматривая любое плос­кое сечение тела, параллельное непо­движной плоскости, называемой основной (рис. 12.1).

Все точки тела, расположенные на пря­мой, перпендикулярной к основной плос­кости, движутся одинаково.

Плоскопараллельное движение изуча­ется двумя методами: методом разложе­ния сложного движения на поступатель­ное и вращательное и методом мгновен­ных центров скоростей.

Метод разложения сложного движения на поступа­тельное и вращательное

Плоскопараллельное движение раскладывают на два движения: поступательное вместе с некоторым полюсом и вращательное от­носительно этого полюса.

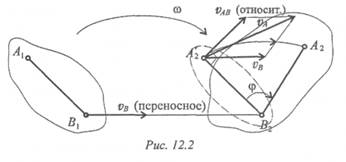
Разложение используют для определения скорости любой точки тела, применяя теорему о сложении скоростей (рис. 12.2).

Точка А движется вместе с точкой В , а затем поворачивается

вокруг В с угловой скоростью ш, тогда абсолютная скорость точки А будет равна

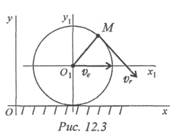
Примером плоскопараллельного движения может быть движе­ние колеса на прямолинейном участке дороги (рис. 12.3).

Скорость точки М v М = v e + v r ,

v_e — скорость центра колеса переносная;

v_r — скорость вокруг центра относительная.

уОх — неподвижная система координат,

у 1 0 1 Х 1 — подвижная система координат, связанная с осью колеса.

Метод определения мгновенного центра скоростей

Скорость любой точки тела можно определять с помощью мгновенного центра скоростей. При этом сложное движение пред­ставляют в виде цепи вращений вокруг разных центров.

Задача сводится к определению положения мгновенного центра вращений (скоростей) (рис. 12.4).

Мгновенным центром скоростей (МЦС) является точка на плоскости, абсолютная скорость которой в дан­ный момент равна нулю.

Вокруг этой точки тело совершает поворот со скоростью ω.

Скорость точки А в данный мо­мент равна v a = ω OA ,

т.к. va — линейная скорость точки А, вращающейся вокруг МЦС.

Существуют три способа определения положения мгновенного центра скоростей.

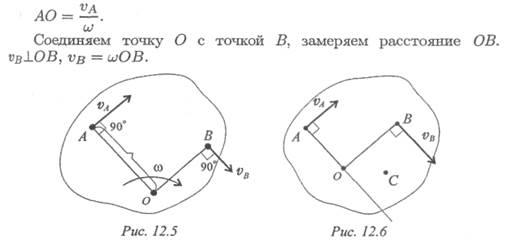
Первый способ. Известна скорость одной точки тела v a и угловая скорость вращения тела ω(рис. 12.5).

Точку О находим на перпендикуляре к вектору скорости v a.

Тема 1.10. Сложное движение точки 89

Второй способ. Известны скорости двух точек тела v a и vB они не параллельны (рис. 12.6).

Проводим из точек А и В два перпендикуляра к известным век­торам скоростей.

На пересечении перпендикуляров находим МЦС. Далее можно найти скорость любой точки

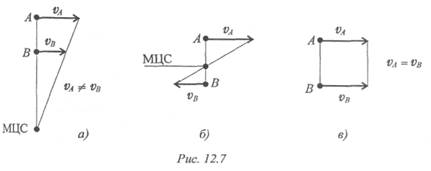
Третий способ. Известны скорости двух точек тела, и они па­раллельны (v a ║ vB) (рис. 12.7).

Соединяем концы векторов, МЦС находится на пересечении ли­нии, соединяющей концы векторов с линией АВ ( рис. 12.7 ). При поступательном движении тела (рис. 12.7в) МЦС отсутствует.

Примеры решения задач

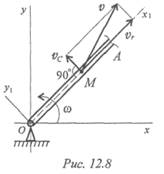
Пример 1. Рассмотрим механизм, в котором стержень ОА вра­щается вокруг точки О со скоростью ω. Вдоль стержня перемеща­ется ползун М со скоростью v m (рис. 12.8). Определить абсолютную скорость точки М.

Решение

1. Относительное движение — вдоль стержня; скорость v_r = v m .

2. Переносное движение — вращение стержня; скорость v_e = ωОМ.

3. Скорость абсолютного движения

Пример 2. Стержень А В соскальзывает вниз, опираясь концами о стену и пол (рис. 12.9). Длина стержня 1,5 м; в момент, изображенный на чертеже, скорость точки В v b = 3 м/с. Найти скорость точки А.

Решение

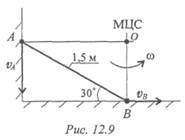
1. Найдем положение МЦС. Скорости точек А и В направлены
вдоль стены и вдоль пола. Восстана­вливая перпендикуляры к векторам
скоростей, находим МЦС.

2. По известной скорости v b определяем угловую скорость ω стержня:

Тема 1.10. Сложное движение точки 91

Контрольные вопросы и задания

1. Какое движение называют сложным?

2. Какие движения твердого тела называют простыми?

3. Какие системы координат выбирают при определении скоростей твердых тел при сложном движении?

4. Какое движение считают переносным, а какое — относительным?

5. Сформулируйте теорему сложения скоростей.

6. Какое движение называют плоским?

7. Какие способы применяют для определения скоростей точек тела при плоско-параллельном движении?

8. Что такое мгновенный центр скоростей, как его определяют и для чего используют?

9. Ответьте на вопросы тестового задания.

Темы 1.10, 1.11. Кинематика.

🔍 Видео

Задачи на движение. Учимся решать задачи на движение. Способы решения задач на движение.Скачать

Закон Сложения Скоростей - Относительная скорость / Урок Физики 10 класс / КинематикаСкачать

Оптимальное обучение вождению. Занятие 10, часть 1. Разворот.Скачать

✓ Суперсложная экономическая задача | В интернете кто-то неправ #031 | Проφиматика и Борис ТрушинСкачать

Определение координаты движущегося тела | Физика 9 класс #3 | ИнфоурокСкачать

Математика 5 класс (Урок№35 - Задачи на движение.)Скачать

Физика - уравнения равноускоренного движенияСкачать

Урок 20 (осн). Усложненные задачи на среднюю скоростьСкачать

Обо всём, как образовалась вселеннаяСкачать

Физика. Задача 1 За 2 с прямолинейного равноускоренного движения тело прошло 20 м увеличив скоростьСкачать

ФИЗИКА 10 класс : Правило сложения скоростей и Относительная скоростьСкачать

Урок 16 (осн) Средняя скорость. Вычисление пути и времени движенияСкачать

УСКОРЕНИЕ 9 класс физика Перышкин движение с ускорениемСкачать

Задачи на движение двух объектовСкачать