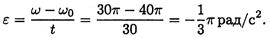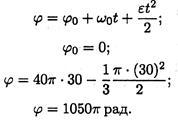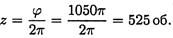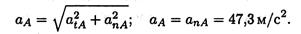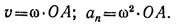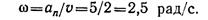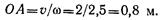Задано уравнение движения тела s f t как определяют скорость и ускорение решение

Пример 1. Ротор электродвигателя вращается со скоростью, описываемой уравнением

Определить вид движения.

Решение

1. Анализируем выражение для скорости: скорость меняется и зависит от времени линейно. Следовательно, угловое ускорение — постоянно, ε = ω’ = 2π = const.

2. Движение равнопеременное (равноускоренное, т.к. ускорение положительно).

Пример 2 Тело вращалось равноускорено из состояния покоя и сделало 360 оборотов за 2 мин. Определить угловое ускорение.

Решение

1. Один оборот равен 2π радиан. Следовательно:

360 оборотов = 720π рад, φ = 720π рад.

2.

Закон равнопеременного вращательного движения

Пример 3. Тело вращалось с угловой частотой 1200 об/мин. Затем движение стало равнозамедленным, и за 30 секунд скорость упала до 900 об/мин. Определить число оборотов тела за это время и время до полной остановки. Использовать пункт 1 примера 3.

Решение

1. Построить график изменения скорости за 30 с (рис. 11.9).

Определяем угловую скорость вращения тела:

Определяем угловое ускорение:

Определяем угол поворота за прошедшее время:

Число оборотов за 30 с:

2. Определяем время до полной остановки.

Скорость при остановке равна нулю, ω = 0.

Пример 5. Маховое колесо вращается равномерно со скоро­стью 120 об/мин (рис. 11.10). Радиус колеса 0,3 м. Определить ско­рость и полное ускорение точек на ободе колеса, а также скорость точки, находящейся на расстоянии 0,15 м от центра.

Решение

Касательное ускорение точки A a_tA = 0; нормальное ускорение точки А а_nA = ω 2 r_A

а_пA = (12,56) 2 • 0,3 = 47,3м/с 2 . 5. Полное ускорение точек на ободе колеса

Пример 9. Точка А, лежащая на ободе равно­мерно вращающегося шкива, движется со скоростью v = 2 м/с и нормальным ускоре­нием а_п = 5 м/с 2 . Определить ра­диус шкива OA и величину угло­вой скорости (рис. 1.46).

Решение

Здесь для решения следует воспользоваться известны­ми соотношениями для линейной скорости и нормального ускорения точек вращающегося тела:

Если второе уравнение разделить на первое, найдем угловую скорость вращения шкива:

Контрольные вопросы и задания

1. Какими кинематическими параметрами характеризуется по­ступательное движение и почему?

2. Запишите уравнение равномерного поступательного движе­ния твердого тела.

3. Запишите уравнение равнопеременного поступательного дви­жения твердого тела.

4. Запишите уравнения равномерного и равнопеременного вра­щательного движений твердого тела.

5. Задано уравнение движения тела S = f(t). Как определяют скорость и ускорение?

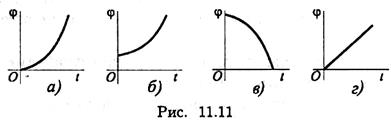
6. Для заданного закона (уравнения) движения

φ = 6,28 + 12t + 3t 2 выберите соответствующий кинематический график движения (рис. 11.11).

Дата добавления: 2017-09-01 ; просмотров: 6357 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №19. Решение задач с помощью производной.

Перечень вопросов, рассматриваемых в теме

1. механический смысл первой производной;
2. механический смысл второй производных;
3. скорость и ускорение.

Глоссарий по теме

Производная y’(x) функции y=f(x) – это мгновенная скорость изменения этой функции. В частности, если зависимость между пройденным путём S и временем t при прямолинейном неравномерном движении выражается уравнением S=f(t), то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени t нужно найти производную S’=f’(x) и подставить в неё соответствующее значение t, то есть v(t)=S’(t).

Производная от данной функции называется первой производной или производной первого порядка. Но производная функции также является функцией, и если она дифференцируема, то от неё, в свою очередь, можно найти производную.

Производная от производной называется второй производной или производной второго порядка и обозначается fили

Производная от второй производной называется производной третьего порядка и обозначается или f»’(x). Производную n-го порядка обозначают f (n) (x) или y (n) .

Если первая производная функции – это мгновенная скорость изменения любого процесса, заданного функцией, то вторая производная – это скорость изменения скорости, то есть ускорение, то есть

Первая производная – это скорость изменения процесса, вторая производная – ускорение. (v= S’; a=v’)

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Давайте вспомним механический смысл производной:

Производная y’(x) функции y=f(x) – это мгновенная скорость изменения этой функции. В частности, если зависимость между пройденным путём S и временем t при прямолинейном неравномерном движении выражается уравнением S=f(t), то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени t нужно найти производную S’=f’(x) и подставить в неё соответствующее значение t, то есть v(t)=S'(t).

Пример 1. Точка движется прямолинейно по закону (S выражается в метрах, t – в секундах). Найти скорость движения через 3 секунды после начала движения.

скорость прямолинейного движения равна производной пути по времени, то есть .

Подставив в уравнение скорости t=3 с, получим v(3)=32+4∙3-1= 20 (м/с).

Пример 2. Маховик, задерживаемый тормозом, поворачивается за t с на угол

Найдите:

а) угловую скорость вращения маховика в момент t = 6 с;

б) в какой момент времени маховик остановится?

Решение: а) Угловая скорость вращения маховика определяется по формуле ω=φ’. Тогда ω=(4t-0,2t 2 )=4-0,4t.

Подставляя t = 6 с, получим ω=4-0,4∙6=1,6 (рад/с).

б) В тот момент, когда маховик остановится, его скорость будет равна нулю (ω=0) . Поэтому 4-0,4t=0.. Отсюда t=10 c.

Ответ: угловая скорость маховика равна (рад/с); t=10 c.

Пример 3. Тело массой 6 кг движется прямолинейно по закону S=3t 2 +2t-5. Найти кинетическую энергию тела через 3 с после начала движения.

Решение: найдём скорость движения тела в любой момент времени t.

Вычислим скорость тела в момент времени t=3. v(3)=6∙3+2=20 (м/с)..

Определим кинетическую энергию тела в момент времени t=3.

Производная второго порядка. Производная n-го порядка.

Производная от данной функции называется первой производной или производной первого порядка. Но производная функции также является функцией, и если она дифференцируема, то от неё, в свою очередь, можно найти производную.

Производная от производной называется второй производной или производной второго порядка и обозначается .

Производная от второй производной называется производной третьего порядка и обозначается y»’ или f»'(x) Производную n-го порядка обозначают f (n) (x) или y (n) .

Примеры. Найдем производные четвёртого порядка для заданных функций:

f'(x)=cos 2x∙(2x)’= 2cos 2x

f (x)=-2sin2x∙(2x)’=-4sin 2x

f»'(x)= -4 cos 2x∙(2x)= -8 cos 2x

f (4) (x)= 8 sin2x∙(2x)’= 16 sin 2x

f (x)= 9∙ 2 3x ∙ln 2 2

f»'(x)= 27∙ 2 3x ∙ln 3 2

f (4) (x)= 81∙ 2 3x ∙ln 4 2

Механический смысл второй производной.

Если первая производная функции – это мгновенная скорость изменения любого процесса, заданного функцией, то вторая производная – это скорость изменения скорости, то есть ускорение, то есть

Итак, первая производная – это скорость изменения процесса, вторая производная – ускорение. (v= S’; a=v’)

Пример 4. Точка движется прямолинейно по закону S(t)= 3t 2 -3t+8. Найти скорость и ускорение точки в момент t=4 c.

найдём скорость точки в любой момент времени t.

Вычислим скорость в момент времени t=4 c.

Найдём ускорение точки в любой момент времени t.

a= v’= (6t-3)’=6 и a(4)= 6 (м/с 2 ) , то есть ускорение в этом случае является величиной постоянной.

Ответ: v=21(м/с); a= v’= 6 (м/с 2 ).

Пример 5. Тело массой 3 кг движется прямолинейно по закону S(t)=t 3 -3t 2 +5. Найти силу, действующую на тело в момент времени t=4 c.

Решение: сила, действующая на тело, находится по формуле F=ma.

Найдём скорость движения точки в любой момент времени t.

v=S’=(t 3 -3t 2 +5)’=3t 2 -6t.

Тогда v(4)=3∙4 2 -6∙4=24 (м/с).

Найдём ускорение: a(t)=v’=(3t 2 -6t)’=6t-6.

Тогда a(4)= 6∙4-6= 18 (м/с 2 ).

Разбор решения заданий тренировочного модуля

№ 1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте

Напишите производную третьего порядка для функции:

f(x)= 3cos4x-5x 3 +3x 2 -8

Решим данную задачу:

f’’’(x)=( 3cos4x-5x 3 +3x 2 -8)’’’=(((3cos4x-5x 3 +3x 2 -8)’)’)’=((-12sin4x-15x 2 +6x)’)’=(-48cos4x-30x)’=192sin4x-30.

№ 2. Тип задания: выделение цветом

Точка движется прямолинейно по закону S(t)= 3t 2 +2t-7. Найти скорость и ускорение точки в момент t=6 c.

1. v=38 м/с; a=6 м/с 2
2. v=38 м/с; a=5 м/с 2
3. v=32 м/с; a=6 м/с 2
4. v=32 м/с; a=5 м/с 2

Решим данную задачу:

Воспользуемся механическим смыслом второй производной:

v= S’(t)=( 3t 2 +2t-7)’=6t+2.

Вычислим скорость в момент времени t=6 c.

Найдём ускорение точки в любой момент времени t.

a= v’= (6t+2)’=6 и a(6)= 6 (м/с 2 ) , то есть ускорение в этом случае является величиной постоянной.

Ответ: v=38(м/с); a= v’= 6 (м/с 2 ).

1. v=38 м/с; a=6 м/с 2
2. v=38 м/с; a=5 м/с 2
3. v=32 м/с; a=6 м/с 2
4. v=32 м/с; a=5 м/с 2

Видео:Скорость движения тела задана уравнениемСкачать

Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях – решение задачи

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Основные законы и формулы, применяемые при решении задач

Вращательное движение вокруг неподвижной оси

Рассмотри твердое тело, вращающееся вокруг неподвижной оси z . Сделаем рисунок. Ось вращения направим перпендикулярно плоскости рисунка, на нас. Пусть φ – угол поворота тела вокруг оси, отсчитываемый от некоторого начального положения. За положительное направление выберем направление против часовой стрелки. Угловая скорость ω равна производной угла поворота по времени t :
.
При , тело вращается против часовой стрелки; при – по часовой. Вектор угловой скорости направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Угловое ускорение ε равно производной угловой скорости по времени:
.
Вектор углового ускорения также направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

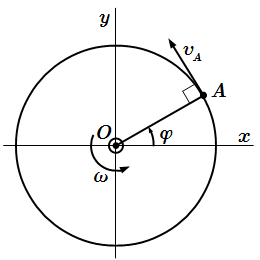
Скорость точки при вращательном движении тела вокруг неподвижной оси

Рассмотрим точку A , принадлежащую твердому телу. Опустим из нее перпендикуляр OA на ось вращения. Пусть – расстояние от точки до оси. Траекторией движения точки A является окружность (или дуга) с центром в точке O радиуса .

Абсолютное значение скорости точки A определяется по формуле:
.
Вектор скорости направлен по касательной к траектории (окружности), перпендикулярно отрезку OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор угловой скорости .

Касательное (или тангенциальное) ускорение точки A определяется аналогично скорости:
.
Оно направлено по касательной к окружности, перпендикулярно OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор углового ускорения .

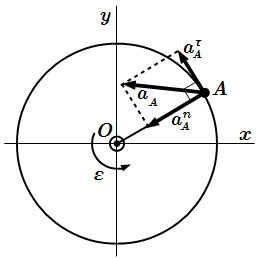
Ускорение точки при вращательном движении тела вокруг неподвижной оси

Нормальное ускорение всегда направлено к центру окружности и имеет абсолютную величину
.

Полное ускорение точки A , или просто ускорение, равно векторной сумме касательного и нормального ускорений:
.
Поскольку векторы и перпендикулярны, то абсолютная величина ускорения точки A определяется по формуле:
.

Поступательное прямолинейное движение

Теперь рассмотрим прямолинейное поступательное движение тела. Направим ось x вдоль его линии движения. Пусть s есть перемещение тела вдоль этой оси относительно некоторого начального положения. Тогда скорость движения всех точек тела равна производной перемещения по времени:
.
При , вектор скорости направлен вдоль оси x . При – противоположно этой оси.

Ускорение точек тела равно производной скорости по времени, или второй производной перемещения по времени:
.
При , вектор ускорения направлен вдоль оси x . При – противоположно.

Соприкосновение тел без проскальзывания

Рассмотрим два тела, находящиеся в зацеплении без проскальзывания. Пусть точка A принадлежит первому телу, а точка B – второму. И пусть, в рассматриваемый момент времени, положения этих точек совпадают. Тогда, если между телами нет проскальзывания, то скорости этих точек равны:
.
Если каждое из тел вращается вокруг неподвижной оси, то равны соответствующие касательные ускорения:
.
Если одно из тел движется поступательно (пусть это второе тело), то ускорение его точек равно касательному ускорению точки соприкосновения первого тела:
.

Видео:Физика - уравнения равноускоренного движенияСкачать

Пример решения задачи

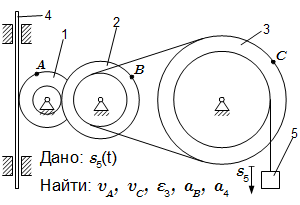
Механизм состоит из ступенчатых колес 1, 2, 3, находящихся в зацеплении и связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 – r₁ = 2 см, R₁ = 4 см, у колеса 2 – r₂ = 6 см, R₂ = 8 см, у колеса 3 – r₃ = 12 см, R₃ = 16 см. На ободьях колес расположены точки A, B и C. Задан закон движения груза: s₅ = t 3 – 6t (см). Положительное направление для s₅ – вниз.

Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.

Указания. Эта задача – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что проскальзывание в ременной передаче и в точках сцепления колес отсутствует. То есть скорости точек колес, находящихся в зацеплении равны, а скорости точек ремня равны скорости точек, лежащих на ободе колес, связанных ременной передачей.

Дано:
t = 2 с; r₁ = 2 см, R₁ = 4 см; r₂ = 6 см, R₂ = 8 см; r₃ = 12 см, R₃ = 16 см; s₅ = t 3 – 6t (см).

Определение скорости и ускорения груза 5

Груз 5 совершает поступательное движение. Поэтому скорости (и ускорения) всех его точек равны. В условии задачи задано смещение s груза относительно некоторого начального положения. Дифференцируя по времени t , находим зависимость скорости точек груза от времени:
.
Дифференцируя скорость груза по времени, находим зависимость ускорения груза от времени:
.

Находим скорость и ускорение груза в заданный момент времени :
см/с;
см/с 2 .

Определение угловых скоростей и ускорений колес

Груз 5 связан нитью с внутренним ободом колеса 3. Поэтому скорости точек внутреннего обода колеса 3 равны скорости груза:
.
Отсюда находим угловую скорость колеса 3 для произвольного момента времени:
.
Здесь подразумевается, что и являются функциями от времени t . Дифференцируя по t , находим угловое ускорение колеса 3:
.
Находим значения угловой скорости и углового ускорения в момент времени с. Для этого подставляем найденные значения и при с:
с –1 ;
с –2 .

Рассмотрим колесо 2. Его внутренний обод связан нитью с внешним ободом колеса 3. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 2 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Рассмотрим колесо 1. Его внутренний обод находится в зацеплении с внешним ободом колеса 2. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 1 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Итак, мы нашли:
ω ₁ = 5.3333 с –1 , ω ₂ = 1.3333 с –1 , ω ₃ = 0.5 с –1 , ε ₁ = 10.6667 с –2 , ε ₂ = 2.6667 с –2 , ε ₃ = 1 с –2 .

Определение скоростей точек A и C

Точка A лежит на окружности радиуса R₁ с центром в точке O₁, расположенной на оси вращения. Поэтому скорость этой точки направлена по касательной к окружности и по абсолютной величине равна
см/с.

Точка C лежит на окружности радиуса R₃ с центром O₃ на оси вращения. Скорость этой точки:
см/с.

Определение ускорения точки B

Точка B лежит на окружности радиуса R₂ с центром O₂, расположенном на оси вращения. Касательное (или тангенциальное) ускорение этой точки направлено по касательной к окружности в сторону, на которую указывает угловое ускорение (по часовой стрелке). По абсолютной величине оно равно
см/с 2 .

Нормальное ускорение всегда направлено к центру окружности. По абсолютной величине оно равно
см/с 2 .

Полное ускорение равно векторной сумме касательного и нормального ускорений:
.
Поскольку касательное ускорение перпендикулярно нормальному, то для абсолютной величины полного ускорения имеем:
см/с 2 .

Определение ускорения рейки 4

Рейка 4 движется поступательно по направляющим. Она находится в зацеплении с внешним ободом колеса 1. Поэтому ее скорость равна скорости точек внешнего обода колеса 1:
.
Дифференцирую по времени, получаем ускорение рейки в произвольный момент времени:
.
Подставляем численные значения для момента времени t = 2 с :
см/с 2 .

см/с; см/с; с –2 ; см/с 2 ; см/с 2 .

Автор: Олег Одинцов . Опубликовано: 25-10-2019

📸 Видео

Траектория и уравнения движения точки. Задача 1Скачать

Скорости и ускорения точек вращающегося телаСкачать

К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Уравнение движенияСкачать

Физика - движение по окружностиСкачать

Решение графических задач на равномерное движениеСкачать

14. Определение скорости и ускорения точки при векторном и координатном способах заданияСкачать

Рассмотрение темы: "Тангенциальное, нормальное и полное ускорение"Скачать

Равномерное прямолинейное движение - физика 9Скачать

Кинематика точки Задание К1Скачать

Кинематика точки. Три способа задания движения. Скорость, ускорениеСкачать

Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Кинематика точки в плоскости. ТермехСкачать

РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ физика 9 ПерышкинСкачать

Уравнение движения. Как найти время и место встречи двух тел ???Скачать