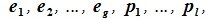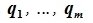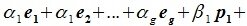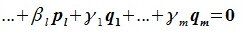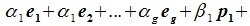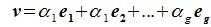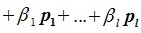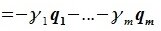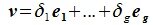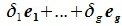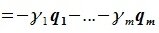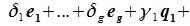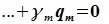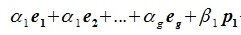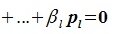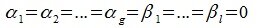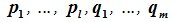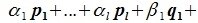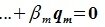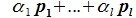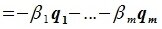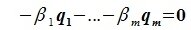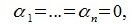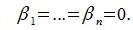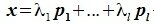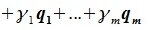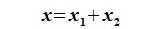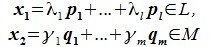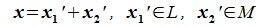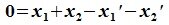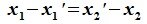Пусть дано N-Мерное линейное пространство L и пусть в нём зафиксирован базис Е = (Е1, Е2, … , Еn ). Пусть М – линейное подпространство в L .
Определение 30. Будем говорить, что Система линейных уравнений задаёт подпространство М, если этой системе удовлетворяют координаты всех векторов из М и не удовлетворяют координаты никаких других векторов.
Из свойств решений однородной системы линейных уравнений следует, что любая однородная линейная система уравнений ранга R с n Переменными задаёт в любом N-Мерном пространстве Ln (если в нём зафиксирован базис) (N–r )-мерное линейное подпространство.
Справедливо и обратное утверждение. А именно, имеет место следующая теорема.
Теорема 30. Если в линейном N-Мерном пространстве Ln Зафиксирован базис, то любое его К-мерное линейное подпространство можно задать системой линейных однородных уравнений с N Неизвестными ранга (N – к).
Доказательство. Пусть в Ln зафиксирован базис Е = (Е1, Е2, … , Еn ). Пусть Lк – линейное К-мерное подпространство в Ln. Выберем в Lк Любой базис А = (А1, а2,… , ак). Пусть 

Так как А – базис, то ранг матрицы А Равен К.
Получили параметрические уравнения, определяющие Lк .
После исключения параметров получится система (N – к) линейных однородных уравнений. Векторы А1, а2, … , ак являются её линейно независимыми решениями. Все остальные решения являются их линейными комбинациями.
Следовательно, система векторов (А1, а2, … , ак) будет фундаментальной системой решений полученной системы уравнений и поэтому ранг этой системы уравнений равен (N – к).
Пример. В пространстве L5 зафиксирован базис Е = (Е1, Е2, е3, е4 , Е5 ). Найти систему линейных однородных уравнений, задающих L3 = , если А1 = (1, –2, 2, 0, 1), А2 = (0, 4, 7, 0, 1), А3 = (–2, 3, –1, 0, 0).
Решение. Найдём ранг системы векторов (А1, а2, а3 ). Для этого достаточно найти ранг матрицы 


D Î L3 Û D = с1А1 + С2А2 + С3А3 . Отсюда D Î L3 Û Х1 = с1 – 2с3 , х2 = –2с1 + 4с2 + 3с3 , х3 = 2с1 + 7с2 – с3 , х4 = 0, х5 = с1 + с2. Если из первого, второго и пятого уравнений выразить С1, с2 и С3 И подставить их в третье и четвёртое уравнения, то получим следующую систему
Замечание. Очевидно, система, задающая данное подпространство, определяется не единственным образом. К найденным уравнениям можно добавлять новые уравнения, являющиеся их линейными комбинациями.
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Способы описания подпространств линейного пространства
Рассмотрим два важных способа описания линейных подпространств, которые условно будем называть внутренним и внешним. В первом (внутреннем) способе используется понятие линейной оболочки векторов, когда все элементы подпространства выражаются через некоторые его элементы (образующие). При втором (внешнем) способе применяются однородные системы уравнений. В этом случае подпространство описывается как пересечение некоторых содержащих его множеств. Для каждого способа описания подпространств укажем методики на хождения размерностей, базисов, алгебраических дополнений, пересечений и сумм подпространств.
Любое n-мерное вещественное линейное пространство изоморфно n-мерному арифметическому пространству . Чтобы установить изоморфизм , достаточно выбрать в пространстве базис и каждому вектору поставить в соответствие его координатный столбец. Поэтому в данном разделе будем рассматривать описание подпространств n-мерного арифметического пространства .
Первый (внутренний) способ. Пусть в пространстве заданы столбцы . Напомним, что для систем столбцов были определены понятия базы (максимальной линейно независимой подсистемы столбцов) и ранга (максимального числа линейно не зависимых столбцов системы), а также методы их нахождения.
Рассматривая линейную оболочку столбцов как линейное подпространство , заключаем, что база системы столбцов является базисом этого подпространства, а ранг системы столбцов равен размерности подпространства .
Поэтому для нахождения размерности и базиса подпространства нужно выполнить следующие действия:
1) составить из данных столбцов матрицу размеров ;
2) привести ее к ступенчатому виду (1.4), используя элементарные преобразования строк;
3) определить размерность и базис подпространства
– количество ненулевых строк в матрице равняется размерности подпространства, т.е. ,
– столбцы матрицы , содержащие единичные элементы (в начале каждой «ступеньки»), определяют номера линейно независимых столбцов матрицы , т.е. искомый базис.
Таким образом, если подпространство задано своими образующими , то его размерность равна рангу системы столбцов , т.е. , а базисом служит максимальная линейно независимая подсистема образующих.
Второй (внешний) способ. Пусть подпространство задано как множество решений однородной системы уравнений с неизвестными. Множество решений системы уравнений можно рассматривать как пересечение подпространств , где — множество решений i-го уравнения системы . Напомним, что любое решение однородной системы представляется в виде линейной комбинации элементов фундаментальной системы решений. Поэтому раз мерность пространства , а базисом служит фундаментальная система решений однородной системы . Способы нахождения фундаментальной системы решений рассмотрены ранее.
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Переход от одного способа описания подпространств к другому
Переход от внутреннего описания к внешнему. Пусть подпространство задано линейной оболочкой столбцов . Требуется составить такую однородную систему уравнений, множество решений которой совпадает с , т.е. . Для этого нужно выполнить следующие действия.
1. Из данных столбцов составить матрицу размеров , а затем блочную матрицу , приписав к матрице единичную матрицу n-го порядка.
2. Элементарными преобразованиями над строками блочной матрицы и первыми ее столбцами привести матрицу к виду , где — простейший вид матрицы .
3. Из последних строк матрицы составить матрицу .
4. Записать искомую систему уравнений .
Поясним содержание алгоритма. Заданное подпространство состоит из линейных комбинаций данных векторов, т.е. все его элементы имеют вид . Решаемую задачу можно сформулировать так: для каких векторов найдутся такие числа , чтобы выполнялось равенство . Другими словами, при каких неоднородная система ( уравнений с неизвестными ) имеет решения? Используя необходимое и достаточное условие (5.24) совместности системы, получаем равенство . Заметим, что решение поставленной задачи неоднозначно, так как существует много однородных систем, имеющих од но и то же множество решений.
Пример 8.8. Подпространство задано линейной оболочкой столбцов . Составить систему уравнений, определяющую подпространство .
Решение. 1. Составляем матрицу и блочную матрицу:
2. Приводим левый блок к простейшему виду. Вычитаем первую строку из остальных, а затем к четвертой строке прибавляем вторую, умноженную на (-2):
Преобразовываем столбцы левого блока: ко второму столбцу прибавим пер вый, умноженный на (-1), к третьему столбцу прибавим первый, умноженный на (-3), а затем второй, умноженный на (-1). Эти преобразования не изменяют правый блок полученной матрицы. Находим простейший вид Л матрицы и матрицу
3. Из последних строк матрицы составляем матрицу искомой системы.
4. Записываем систему уравнений Заданные в условии примера столбцы являются решениями полученной системы, в чем можно убедиться при их подстановке в систему уравнений вместо .
Переход от внешнего описания к внутреннему. Пусть подпространство задано как множество решений однородной системы т уравнений с л неизвестными: . Требуется найти размерность и базис этого подпространства, т.е. представить его в виде линейной оболочки . Для этого нужно выполнить следующие действия.
1. Найти фундаментальную систему решений однородной системы . Искомая размерность .
2. Представить заданное пространство как линейную оболочку .
Первый пункт алгоритма удобно выполнять следующим образом:
– составить блочную матрицу , приписав к матрице единичную матрицу n-го порядка;
– элементарными преобразованиями над столбцами блочной матрицы и строками верхнего блока привести матрицу к виду , где — простейший вид матрицы ;
– из последних столбцов матрицы составить фундаментальную матрицу .
Столбцы фундаментальной матрицы составляют искомую фундаментальную систему решений.
Заметим, что решение поставленной задачи неоднозначно, так как существует много базисов одного и того же линейного подпространства.
Пример 8.9. Найти размерность и базис подпространства , заданного системой уравнений
Решение. 1. Фундаментальная матрица для этой системы была найдена в примере 5.6
Ее столбцы образуют фундаментальную систему решений. Размерность подпространства равна , .
2. Столбцы являются искомым базисом, так как они линейно независимы и .
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Подпространство линейного пространства
Видео:Решение систем уравнений методом подстановкиСкачать

Определение и размерность подпространства
Определение 6.1. Подпространством L n-мерного пространства R называется множество векторов, образующих линейное пространство по отношению к действиям, которые определены в R.
Другими словами, L называется подпространством пространства R, если из x, y∈L следует, что x+y∈L и если x∈L, то λ x∈L, где λ— любое вещественное число.
Простейшим примером подпространства является нулевое подпространство, т.е. подмножество пространства R, состоящее из единственного нулевого элемента. Подпространством может служить и все пространство R. Эти подпространства называются тривиальными или несобственными.
Подпространство n-мерного пространства конечномерно и его размерность не превосходит n: dim L≤ dim R.
Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

Сумма и пересечение подпространств
Пусть L и M — два подпространства пространства R.
Cуммой L+M называется множество векторов x+y, где x∈L и y∈M. Очевидно, что любая линейная комбинация векторов из L+M принадлежит L+M, следовательно L+M является подпространством пространства R (может совпадать с пространством R).
Пересечением L∩M подпространств L и M называется множество векторов, принадлежащих одновременно подпространствам L и M (может состоять только из нулевого вектора).
Теорема 6.1. Сумма размерностей произвольных подпространств L и M конечномерного линейного пространства R равна размерности суммы этих подпространств и размерности пересечения этих подпространств:
dim L+dim M=dim(L+M)+dim(L∩M).
Доказательство. Обозначим F=L+M и G=L∩M. Пусть G g-мерное подпространство. Выберем в нем базис 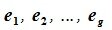
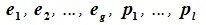
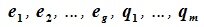
составляют базис F=L+M. Для того, чтобы векторы (6.1) составляли базис пространства F они должны быть линейно независимы и любой вектор пространства F можно представить линейной комбинацией векторов (6.1).
Докажем линейную независимость векторов (6.1). Пусть нулевой вектор пространства F представляется линейной комбинацией векторов (6.1) с некоторыми коэффициентами:
Левая часть (6.3) является вектором подпространства L, а правая часть является вектором подпространства M. Следовательно вектор
принадлежит подпространству G=L∩M. С другой стороны вектор v можно представить линейной комбинацией базисных векторов подпространства G:
Из уравнений (6.4) и (6.5) имеем:
Но векторы 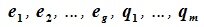
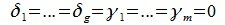
В силу линейной независимости базиса подпространства L имеем:
Так как все коэффициенты в уравнении (6.2) оказались нулевыми, то векторы
линейно независимы. Но любой вектор z из F (по определению суммы подпространств) можно представить суммой x+y, где x∈L, y∈M. В свою очередь x представляется линейной комбинацией векторов 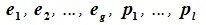
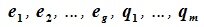
Изучая базисы подпространств L и M и базис подпространства F=L+M (6.10), имеем: dim L=g+l, dim M=g+m, dim (L+M)=g+l+m. Следовательно:
dim L+dim M−dim(L∩M)=dim(L+M). ■
Видео:4.1 Сумма и пересечение подпространств.Скачать

Прямая сумма подпространств
Определение 6.2. Пространство F представляет собой прямую сумму подпространств L и M, если каждый вектор x пространства F может быть единственным способом представлен в виде суммы x=y+z, где y∈ L и z∈M.
Прямая сумма обозначается L⊕M. Говорят, что если F=L⊕M, то F разлагается в прямую сумму своих подпространств L и M.
Теорема 6.2. Для того, чтобы n-мерное пространство R представляло собой прямую сумму подпространств L и M, достаточно, чтобы пересечение L и M содержало только нулевой элемент и чтобы размерность R была равна сумме размерностей подпространств L и M.
Доказательство. Выберем некоторый базис 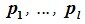
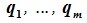
является базисом пространства R. По условию теоремы размерность пространства R n равна сумме подпространств L и M (n=l+m). Достаточно доказать линейную независимость элементов (6.11). Пусть нулевой вектор пространства R представляется линейной комбинацией векторов (6.11) с некоторыми коэффициентами:
Так как левая часть (6.13) является вектором подпространства L, а правая часть — вектором подпространства M и L∩M= 0, то
Но векторы 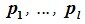
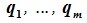
Установили, что (6.12) справедливо лишь при условии (6.15), а это доказывает линейную независимость векторов (6.11). Следовательно они образуют базис в R.
Пусть x∈R. Разложим его по базису (6.11):
Из (6.17) и (6.18) следует, что любой вектор из R можно представить суммой векторов x1∈L и x2∈M. Остается доказать что это представление является единственным. Пусть кроме представления (6.17) есть и следующее представление:
Вычитая (6.19) из (6.17), получим
Так как 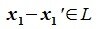
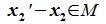
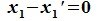
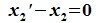
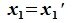
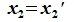
🔥 Видео
Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Базисные решения систем линейных уравнений (03)Скачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Решение системы линейных уравнений. Подстановка. С дробными выражениями.Скачать

Решение системы неравенств с двумя переменными. 9 класс.Скачать

Решение однородных линейных систем. ТемаСкачать

Решение систем уравнений методом сложенияСкачать

Фундаментальная система решений системы линейных уравнений ФСР СЛАУСкачать

Базис линейного пространства (01)Скачать

Построение угла, равного данному. 7 класс.Скачать

Решение системы уравнений методом ГауссаСкачать

Система уравнений. Метод алгебраического сложенияСкачать

Решение систем уравнений. Методом подстановки. Выразить YСкачать