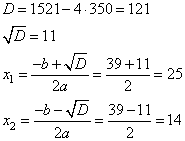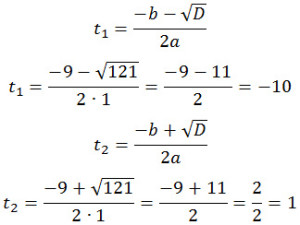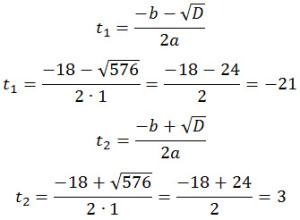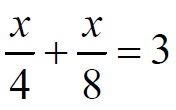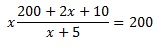Задание. Решите систему уравнений
ОДЗ системы уравнений – все числа.
Для решения данной системы уравнений воспользуемся способом сложения. При решении этим способом мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.
В уравнениях данной системы коэффициенты при y являются противоположными числами. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной:
Подставив в любое из уравнений системы вместо x число -2, найдем y:
Подставив в любое из уравнений системы вместо x число 2, найдем y:
- Разбор задания №21 ОГЭ
- Математика: теория и методика преподавания в образовательной организации
- Дистанционное обучение как современный формат преподавания
- Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Задание №21 ОГЭ по математике
- 🔥 Видео
Видео:ОГЭ Задание 21 Система уравненийСкачать

Разбор задания №21 ОГЭ
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
Задание 21. Решите систему уравнений
Для решения данной системы можно вычесть второе уравнение из первого, это позволит избавиться от переменной y, получим:
Решаем квадратное уравнение через дискриминант, имеем два корня:
Для каждого из найденных корней найдем соответствующее значение y, подставив 

Задание 21. Решите систему уравнений
Так как оба уравнения равны одному и тому же значению y, то их можно приравнять, получим:

Полученное выражение будет равно 0, если

Найдем теперь значения y для каждого x, имеем:

Задание 21. Решите систему уравнений
Разделим первое уравнение на 2, а второе – на 4, получим:
Видим, что у обоих уравнений есть слагаемое 
Теперь вычислим значение y при x=2, подставив x в первое уравнение, имеем:

Таким образом, имеем решение (2, -2), (2,2).
Задание 21. Решите систему уравнений
Разделим второе уравнение на 2, получим систему
и вычтем из первого уравнения второе:
Для значения x=2 найдем соответствующие значения y, подставив x в первое уравнение:
То есть имеем два решения: (2;-3) и (2;3).
Задание 21. Решите уравнение
Преобразуем уравнение, приведем его к следующему виду:
Полученное выражение будет равно 0, если
Таким образом, получили следующие корни: -4; -3; 2.
Задание 21. Решите уравнение 
Упростим выражение, перепишем его в следующем виде:
Полученное выражение будет равно 0, если
Получили три корня: -5; -4; 3.
Задание 21. Решите систему уравнений
Сложим оба уравнения, получим:
Для найденных корней x вычислим из первой формулы соответствующие значения y, имеем:
— для 

— для 

Получили два решения: (-1;5), (1;5).
Задание 21. Решите систему уравнений
Сложим оба уравнения, получим:
Вычислим соответствующие значения y при x=-2 и 2, подставив эти значения в первую формулу системы:
— при x=-2: 
— при x=2: 
Имеем следующие решения: (-2; 3) и (2; 3).
Задание 21. Решите неравенство 
Можно заметить, что данное неравенство будет больше либо равно 0, если

Преобразуем данное выражение, перепишем его в виде:
Из последнего выражения имеем две точки, делящие числовую ось:


Ответ: 
Задание 21. Решите неравенство
Сложим оба уравнения системы, избавимся таким образом от переменной y, получим:
Теперь, для каждого из найденных x, вычислим y из первого уравнения:
Получаем решения: (-1; 8), (1; 8).
Задание 21. Решите неравенство
Сложим оба уравнения системы, избавимся от переменной y, получим:
Для каждого найденного корня x вычислим соответствующее значение y из первого уравнения, имеем:
То есть получили следующие решения: (-2; 1), (2; 1).
Задание 21. Найдите значение выражения 28a-7b+40, если 
Приведем выражение 

Задание 21. Найдите значение выражения 33a-23b+71, если 
Приведем выражение 

Задание 21. Решите уравнение 
Учитывая, что слагаемые в уравнении всегда больше либо равны 0, то уравнение будет равно нулю, если каждое из слагаемых равно нулю. Соответственно, получаем следующую систему уравнений:
Из первого уравнения имеем корни
Из второго уравнения, получаем следующие два корня:
Из полученных значений видно, что оба уравнения одновременно будут принимать значение 0 при x=-5.
Задание 21. Решите уравнение 
Любое число в квадрате всегда больше 0, следовательно, уравнение будет равно 0, если оба слагаемых равны 0. Это условие можно записать в виде следующей системы:
Из первого уравнения получаем два корня:
Из второго уравнения, имеем корни:
Общий корень, при котором оба уравнения переходят в 0, равен -4.
Задание 21. Решите уравнение 
Упростим уравнение, приведем его к следующему виду:
Данное уравнение будет равно 0, если
Решаем первое квадратное уравнение, получаем корни:
Оба корня удовлетворяют неравенству 
Ответ: 
Задание 21. Решите уравнение 
Преобразуем уравнение к виду
Данное уравнение будет равно 0, если
Найдем корни уравнения из квадратного уравнения:
Оба корня не равны 0, следовательно, являются решениями уравнения.
Ответ: 
Задание 21. Решите уравнение 
Сначала преобразуем выражение, получим:
Последнее выражение показывает, что уравнение будет равно 0, если хотя бы один из множителей будет равен 0, то есть имеем 3 уравнения и 3 корня:
Задание 21. Решите уравнение 
Сначала выполним преобразование уравнения, получим:
Последнее выражение показывает, что уравнение будет равно, если хотя бы один из множителей равен 0, то есть имеем следующие три уравнения:
Задание 21. Решите неравенство 
Преобразуем неравенство, приведем его к виду:
Полученное выражение дает две точки, делящие числовую ось:

Ответ: 
Задание 21. Решите неравенство 
Перепишем неравенство в следующем виде:
Из последнего выражения имеем две точки, делящие числовую ось:

Ответ: 
Задание 21. Решите уравнение 
Выполним следующее преобразование уравнения:
Полученное выражение будет равно 0, если хотя бы один из множителей равен 0, то есть имеем три уравнения и три корня:
Задание 21. Решите уравнение 
Перепишем уравнение в следующем виде:
Последнее выражение принимает нулевое значение, когда хотя бы один из множителей равен 0, то есть имеем три следующих корня:
Задание 21. Решите уравнение 
Решим уравнение при условии, что 
Решим квадратное уравнение с помощью дискриминанта, имеем:
Значение 7 не входит в диапазон 
Задание 21. Решите уравнение 
1. Запишем ОДЗ уравнения:
2. Упростим уравнение, приведем его к виду:
Решаем квадратное уравнение, имеем два корня:
Из двух корней только второй 
Задание 21. Решите уравнение 
Так как каждое из слагаемых всегда больше либо равно 0, то уравнение будет равно нулю только если оба слагаемых равны 0, то есть данное уравнение можно записать в виде следующей системы:
Упрощаем данные выражения, имеем:
Имеем один общий корень -3, при котором оба уравнения одновременно равны 0, то есть этот корень есть решение уравнения.
Задание 21. Решите уравнение 
Каждое из слагаемых уравнения всегда больше либо равно 0, следовательно, уравнение будет равно 0, только если оба слагаемых равны 0. Запишем это положение в следующем виде:
Упростим выражения, получим:
Первое уравнение дает два корня
Второе уравнение также дает два корня:
В результате получаем один общий корень 
Задание 21. Решите уравнение 
Упростим выражение, запишем его в виде:
Последнее выражение будет равно 0, если хотя бы один из множителей равен 0, то есть имеем два уравнения:
Таким образом, получили три корня уравнения -2; -1; 1.
Задание 21. Решите уравнение 
Перепишем уравнение в следующем виде:
Последнее выражение будет равно 0, если хотя бы одна из скобок будет равна 0, то есть имеем следующие два уравнения:
Таким образом, получили три корня уравнения -5; -2; 2.
Задание 21. Найдите значение выражения 61a-11b+50, если 
Упростим выражение 
Чтобы привести выражение к виду 
То есть получили значение 10.
Задание 21. Найдите значение выражения 39a-15b+25, если 
Преобразуем выражение 
Чтобы получить выражение вида 
Задание 21. Решите уравнение 
1. Запишем ОДЗ уравнения
2. Упростим уравнение, получим:
Решаем квадратное уравнение, имеем два корня:
ОДЗ удовлетворяет только один корень -3.
Задание 21. Решите уравнение 
1. ОДЗ уравнения
2. Упростим уравнение, получим:
Решаем квадратное уравнение, имеем два корня:
ОДЗ принадлежит только один корень уравнения -3.
Задание 21. Найдите значение выражения 19a-7b+12, если 
Перепишем выражение 
Приведем последнее выражение к виду 
Задание 21. Найдите значение выражения 25a-5b+22, если 
Упростим выражение 
Чтобы привести последнее выражение к виду 
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 691 человек из 75 регионов
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 861 человек из 78 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Сейчас обучается 51 человек из 23 регионов
«Мотивация здорового образа жизни. Организация секций»
Свидетельство и скидка на обучение каждому участнику
- Для всех учеников 1-11 классов
и дошкольников - Интересные задания
по 16 предметам
«Как закрыть гештальт: практики и упражнения»
Свидетельство и скидка на обучение каждому участнику
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 841 579 материалов в базе
Ищем педагогов в команду «Инфоурок»
Другие материалы
- 26.09.2019
- 142
- 0
- 26.09.2019
- 195
- 0
- 26.09.2019
- 272
- 11
- 26.09.2019
- 562
- 28
- 26.09.2019
- 161
- 0
- 26.09.2019
- 219
- 1
- 26.09.2019
- 714
- 10
- 26.09.2019
- 165
- 2
«Учись, играя: эффективное обучение иностранным языкам дошкольников»
Свидетельство и скидка на обучение
каждому участнику
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 26.09.2019 2282
- DOCX 138.9 кбайт
- 100 скачиваний
- Рейтинг: 5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Шамченко Елена Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 2 года и 6 месяцев
- Подписчики: 1
- Всего просмотров: 27098
- Всего материалов: 31
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Задание 21. Уравнения и системы уравнений. Подготовка к ОГЭ 2020. Вебинар | МатематикаСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу
Время чтения: 1 минута
С 1 сентября в российских школах будут исполнять гимн России
Время чтения: 1 минута
Госдума рассматривает проект о регулировании «продленок» в школах
Время чтения: 1 минута
Вузы РФ не будут повышать стоимость обучения на первом курсе
Время чтения: 1 минута
Около 20% детей до 15 лет не воспринимают прочитанную информацию
Время чтения: 1 минута
Российские школьники начнут изучать историю с первого класса
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:ОГЭ задача 21 (системы уравнений) #3Скачать

Задание №21 ОГЭ по математике
В двадцать втором задании необходимо решить задачу, составив уравнение с неизвестными. Ниже мы приводим алгоритмы решения типовых вариантов.
Алгоритм решения:
- Введем неизвестную величину: скорость третьего.
- Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
- Выясняем, на какой
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Решение:
1. Обозначим через x км/ч скорость третьего велосипедиста. 2. Составим таблицу их краткого условия:
| v, км/ч | t, ч | S, км |
| 1 велосипедист | 21 | На 2 ч раньше всех |
| 2 велосипедист | 15 | На 1 ч раньше третьего |
| 3 велосипедист | х |
3. Задача на движение водном направлении, значит, для определения совместной скорости (сближения), необходимо из большей скорости вычитать меньшую. Наибольшая скорость была у третьего велосипедиста, потому что он догонял двух других.
4. Перед тем, как выехал третий велосипедист, первый двигался уже 2 часа. За это время он проехал 42 км, а второй проехал 15 км, поскольку был в пути 1 час. Совместная скорость третьего и второго велосипедистов равна (x-15) км/ч. так как они движутся в одном направлении. Третий велосипедист догнал второго спустя 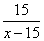
Совместная скорость третьего и первого велосипедистов равна (x-21)км/ч. Третий велосипедист догнал первого через 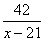
По условию третий велосипедист догнал первого спустя 9 ч после того, как догнал второго.
5. Исходя из этого, составим равенство:
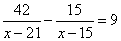
Преобразуем полученное уравнение:
6. Получили квадратное уравнение. Решим его:
По условию скорость третьего велосипедиста была наибольшей, значит, второй
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Введем неизвестные величины: скорость третьего и время его движения.
- Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
- Используя условие, формулы времени или скорости, выражаем через неизвестные величины все остальные.
- Исходя из условия, составляем равенства.
- Составляем и решаем систему уравнений.
- Определяем величины, которые еще нужно найти.
- Записываем ответ.
Решение:
1. Пусть x км/ч – скорость третьего велосипедиста, а t ч – время, за которое он догнал второго велосипедиста.
2. Составим таблицу данных условия:
| v, км/ч | t, ч | s, км |
| 1 велосипедист | 15 | t +7 |
| 2 велосипедист | 10 | t +1 |
| 3 велосипедист | х | t |
3. До места встречи со вторым велосипедистом третий проехал x·t км.
Скорость второго велосипедиста 10 км/ч. В пути он находился t + 1 часов к моменту встречи с третьим велосипедистом. Тогда в момент встречи велосипедисты находились на расстоянии 10·(t + 1) км от поселка. Расстояния эти одинаковы, значит, x·t = 10·(t + 1).
Первого велосипедиста третий догонит через t + 5 ч – время, за которое он догнал первого велосипедиста после второго, тогда до места встречи с первым велосипедистом третий проехал x·(t + 5) км.
Первый велосипедист ехал со скоростью 15 км/ч и был в пути до встречи с третьим t + 7 часов, потому как выехал он на 2 часа раньше. Расстояние, которое проехал первый велосипедист, равно 15·(t + 7) км.
Получаем еще одно равенство: x·(t + 5) = 15·(t + 7)
4. Составляем систему уравнений:
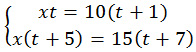

Подставляем вместо x в первое уравнение системы правую часть равенства и решаем полученное уравнение.
(t + 19)·t = 10t + 10
t 2 + 19t = 10t + 10
По формуле дискриминанта и корней:
D = 9 2 — 4·1·(-10) = 81 + 40 = 121
Первый ответ не может удовлетворять условию задачи, поскольку время не может иметь отрицательных значений. Следовательно,
x = t + 19 = 1 + 19 = 20
Скорость третьего велосипедиста 20 км/ч.
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Введем неизвестные величины: скорость третьего и время его движения.
- Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
- Используя условие, формулы времени или скорости, выражаем через неизвестные величины все остальные.
- Исходя из условия, составляем равенства.
- Составляем и решаем систему уравнений.
- Определяем величины, которые еще нужно найти.
- Записываем ответ.
Решение:
1. Пусть x км/ч – скорость третьего велосипедиста, а t ч – время, за которое он догнал второго велосипедиста. 2. Составим таблицу данных условия:
| v, км/ч | t, ч | s, км |
| 1 велосипедист | 24 | t +9 |
| 2 велосипедист | 21 | t +1 |
| 3 велосипедист | х | t |
3. До места встречи со вторым велосипедистом третий проехал x·t км. Второй велосипедист до момента, когда его догонит третий велосипедист, двигался t + 1 часов . Он проехал до места встречи 21·(t + 1) км. Расстояния, пройденные велосипедистами, одинаковы. Получим первое равенство x·t = 21·(t + 1). Третий велосипедист до момента встречи с первым велосипедистом после встречи о вторым, ехал t + 9 ч тогда до места встречи с первым велосипедистом он проехал расстояние x·(t + 9) км. Первый велосипедист до встречи с третьим ехал t + 11 часов, поскольку до момента выезда третьего, уже проехал 2 часа. До места встречи он проехал 24·(t + 11) км. Расстояния одинаковы. Тогда получим еще одно равенство: x·(t + 9) = 24·(t + 11) Составим систему уравнений для решения задачи: 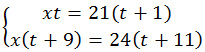
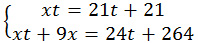
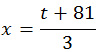
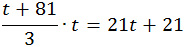
t 2 + 81t = 63t + 63
t 2 + 18t – 63 = 0
D = 18 2 — 4·1·(-63) = 324 + 252 = 576
Первое значение не подходит, поскольку время по условию не может иметь отрицательные значения. Значит, 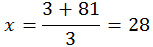
pазбирался: Даниил Романович | обсудить разбор | оценить
Пусть искомое расстояние равно x км. Скорость лодки при движении против течения равна 4 км/ч, при движении по течению равна 8 км/ч. Время, за которое лодка доплывёт от места отправления до места назначения и обратно, равно
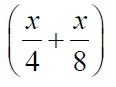
Из условия задачи следует, что это время равно 3 часам. Составим уравнение:
Решая уравнение, получаем x = 8.
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Находим число процентов (или долю) твердого вещества в свежих фруктах. Находим эту величину в кг.
- Вычисляем кол-во процентов твердого вещества в сушеных фруктах.
- Составляем пропорцию и определяем общую массу сушеных фруктов.
Решение:
В сушеных фруктах масса твердого вещества, по сравнению со свежими, не меняется (а только снижается объем воды). Поэтому в искомой массе сухих фруктов мякоти тоже будет 4,2 кг. Но в процентном соотношении эта масса составит 100%–30%=70% (30% по условию приходится на воду). Искомая же (общая) масса сухих фруктов в данном случае – это 100%.
Тогда обозначим искомую массу через Х и составим пропорцию: 4,2 кг – 70% Х – 100%
Решим эту пропорцию:
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Вводим переменные-обозначения для скорости наполнения резервуара (л/мин) и для времени наполнения (мин). Выражаем через соответствующие переменные параметры наполнения для 1-й и 2-й труб.
- Составляем систему уравнений (1-е уравнение для первой трубы, 2-е – для второй).
- Решаем систему.
Решение:
Обозначим через х скорость наполнения 1-й трубы (это наша искомая величина). Тогда скорость наполнения 2-й трубы равна (х+5).Обозначим через t время наполнения 2-й трубы. Тогда время наполнения 1-й трубы составит (t+2).
Через каждую из труб должно пройти 200 л воды. Для 1-й трубы получим:
Аналогично для 2-й трубы:
Из уравнения для 2-й трубы выразим t через х:
Подставим полученное для t выражение в уравнение для 1-й трубы: 
Корень х2 не может быть принят в качестве ответа, поскольку он не удовлетворяет условию (скорость наполнения резервуара не может быть отрицательной величиной).
Значит, искомая скорость наполнения равна 20 л/мин.
pазбирался: Даниил Романович | обсудить разбор | оценить
Составим для удобства решения таблицу, в которую внесем данные из условия задачи, обозначив переменной х неизвестную величину – скорость 1 автомобиля:
| Скорость | Время | Расстояние | |
| 1 автомобиль | х | 800 х . . | 800 |
| 2 автомобиль | х – 36 | 800 х − 36 . . | 800 |
Пояснения к заполнению таблицы:
Так как мы обозначили за х скорость 1 авто, значит скорость 2 авто будет на 36 км/ч меньше.
Расстояние у каждого авто будет 800 км.
Для нахождения времени надо расстояние разделить на скорость, поэтому мы получили дроби с переменной в знаменателе.
Зная, что первый прибывает к финишу на 5 ч раньше второго, составим и решим уравнение:
800 х − 36 . . − 800 х . . = 5
Приведем к общему знаменателю х(х-36) наше уравнение и решим его:
800х – 800х+28800=5х 2 – 180
5х 2 – 180 – 28800 =0; разделим на 5 каждый коэффициент:
Решим полученное квадратное уравнение
D=b 2 – 4ac=36 2 – 4 ∙ ( − 5760 ) =24336
х1,2= − b ± √ D 2 a . . = 36 ± 156 2 . .
Отсюда х1=96, а х2 не удовлетворяет условию задачи, так как оно отрицательное, а скорость не может быть выражена отрицательным числом.
Значит, скорость первого автомобиля 36 км/ч
pазбирался: Даниил Романович | обсудить разбор | оценить
🔥 Видео
ОГЭ Задание 21 Системы уравненийСкачать

ОГЭ Задание 21 Система уравненийСкачать

ОГЭ Задание 21 Системы уравнений 1Скачать

21 задание ОГЭ математика | Задачи на процентыСкачать

ОГЭ Задание 21 Система уравнений Метод заменыСкачать

21 задание из ОГЭ по математике 2024. Текстовые задачиСкачать

ОГЭ Задание 21 Система уравнений Метод заменыСкачать

Задачи на движение из второй части. Задание 21 | Математика ОГЭ 2023 | УмскулСкачать

ОГЭ Задание 21 Система уравнений Разделим первое уравнение системы на второе уравнениеСкачать

Такие задачи точно будут на ОГЭ 2023! / Разбираем 21 задание на ОГЭ по математикеСкачать

ОГЭ задание 21 Системы уравнений 3Скачать

ОГЭ Задание 21 Симметрическая система уравненийСкачать

Задание 21 ОГЭ по математике #30Скачать

Задание 21 ОГЭ по математике #26Скачать

ОГЭ по математике. Задание 21. Вар. 2 Решите Систему уравнений.Скачать

ОГЭ Задание 21 Системы уравнений (6)Скачать