Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.
Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.
Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.
Что необходимо помнить при решении уравнений?
1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть — помним, что он существует, только если
2) Стараемся записывать решение в виде цепочки равносильных переходов.
3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.
4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.
5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка . От нее и будем отсчитывать. Получим:
6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Упростим левую часть по формуле приведения.
Вынесем за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Видим, что указанному отрезку принадлежат решения
Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка От нее и отсчитываем.
2. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.
Степени равны, их основания равны. Значит, равны и показатели.
Это ответ в пункте (а).
б) Отберем корни, принадлежащие отрезку
Отметим на тригонометрическом круге отрезок и найденные серии решений.
Видим, что указанному отрезку принадлежат точки и из серии
Точки серии не входят в указанный отрезок.
А из серии в указанный отрезок входит точка
Ответ в пункте (б):
3. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Применим формулу косинуса двойного угла:
Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.
Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.
б) Для разнообразия отберем корни на отрезке с помощью двойного неравенства.
Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».
Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.
Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии на отрезке Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.
4. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть
Уравнение равносильно системе:
Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых 
, то есть те, что соответствуют точкам справа от оси .
Ответ в пункте а)
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки
5. а) Решите уравнение
б) Найдите корни, принадлежащие отрезку
Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Это значит, что уравнение равносильно системе:
Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых или . Заметим, что среди них находятся и углы, для которых
Числа серии не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.
Тогда в ответ в пункте (а) войдут серии решений:
б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.
Видео:Рациональные уравнения / Тип 12 ЕГЭ профиль #519423Скачать
Путеводитель по задачам С1
Список всех тригонометрических задач (С1), разобранных на сайте (список пополняется)
!!Смотрите также сборник заданий С1 ЕГЭ по математике !!
Смешное видео по теме
-11. (Реальный ЕГЭ, 2021)
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
-10. (Реальный ЕГЭ, 2021)
а) Решите уравнение 
б) Найдите его корни на промежутке 
Решение
-9. ( Демо ЕГЭ, 2020)
a) Решите уравнение 
б) Найдите его корни на промежутке 
. Видеорешение
-8. (Реальный ЕГЭ, 2019)
a) Решите уравнение 
б) Найдите его корни на промежутке 
. Решение
-7. (Реальный ЕГЭ, 2019)
a) Решите уравнение 
б) Найдите его корни на промежутке 
. Решение
-6. (Реальный ЕГЭ, 2018)
a) Решите уравнение 
б) Найдите его корни на промежутке 
. Решение
-5. (Досрочный резервный ЕГЭ, 2018)
a) Решите уравнение 
б) Найдите его корни на промежутке 
. Решение
-4. (Досрочный ЕГЭ, 2018)
a) Решите уравнение 
б) Укажите все корни этого уравнения, принадлежащие промежутку 
. Решение
-3. (Резервный ЕГЭ, 2017)
а) Решите уравнение 
б) Найдите корни уравнения из отрезка 
Решение
-2. (Реальный ЕГЭ, 2017)
а) Решите уравнение 
б) Найдите корни уравнения из отрезка 
Решение
-1. (Реальный ЕГЭ, 2017)
а) Решите уравнение 
б) Найдите корни уравнения из отрезка 
Решение
0. (Досрочн. ЕГЭ, 2017)
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение
1. (Резервн. ЕГЭ, 2016)
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение
2. (ЕГЭ, 2016)
а) Решите уравнение: 
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение
3. (Т/Р, апрель 2016)
а) Решите уравнение 
б) Найдите все корни этого уравнения, принадлежащие отрезку 
Решение
4. (Досрочн. ЕГЭ, 2016)
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение
5. (ЕГЭ, 2015)
а) Решите уравнение 
.
б) Найдите все корни этого уравнения, принадлежащие промежутку Решение
6. (Диагностическая, 2015)
а) Решите уравнение 
б) Найдите все корни уравнения, принадлежащие отрезку 
Решение
7. (ДЕМО, 2014)
a) Решите уравнение 
.
б) Найдите все корни этого уравнения, принадлежащие промежутку 
. Решение
8. (Диагностическая, 2014)
a) Решите уравнение 
б) Найдите все корни этого уравнения, принадлежащие отрезку 
Решение
9. (Диагностическая, 2013)
a) Решите уравнение: 
б) Найдите все корни этого уравнения, принадлежащие отрезку 
Решение
10. (Диагностическая, 2013)
а) 
б) Найдите все корни этого уравнения, принадлежащие отрезку [-1; 2]. Решение
11. (ЕГЭ, 2013)
a) Решить уравнение 
.
б) Найдите все корни этого уравнения, принадлежащие отрезку 
. Решение
12. (Т/Р А. Ларина)
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 
13. (Т/Р А. Ларина)
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение
14. (Т/Р А. Ларина)
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение
15. (Т/Р А. Ларина)
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
16. (Т/Р А. Ларина)
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение
17. (Т/Р А. Ларина)
а) Решите уравнение 
б) Найдите его корни, принадлежащие отрезку 
Решение
18. (Т/Р А. Ларина)
a) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие интервалу 
Решение
19. (Т/Р А. Ларина)
a) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие интервалу 
Решение
20. (Т/Р А. Ларина)
a) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение
21. (Т/Р А. Ларина)
a) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение
22. (Т/Р А. Ларина)
а) Решите уравнение 
.
б) Укажите корни уравнения, принадлежащие отрезку 
Решение
23. (Т/Р А. Ларина)
а) Решите уравнение 
.
б) Укажите корни уравнения, принадлежащие промежутку 
Решение
24. (Т/Р А. Ларина)
а) Решите уравнение 
.
б) Укажите корни уравнения, принадлежащие промежутку 
Решение
25. (Т/Р А. Ларина)
а) Решите уравнение 
.
б) Укажите корни уравнения, принадлежащие промежутку 
Решение
26. (Т/Р А. Ларина)
а) Решите уравнение 
б) Укажите корни уравнения, принадлежащие промежутку 
Решение
27. (Т/Р А. Ларина)
Найдите все корни уравнения 
удовлетворяющие неравенству 
Решение
28. (Т/Р А. Ларина)
a) Решите уравнение 
б) Укажите корни уравнения, принадлежащие отрезку 
Решение
29. (Т/Р А. Ларина)
a) Решите уравнение 
б) Укажите корни уравнения, принадлежащие отрезку 
Решение
30. (Т/Р А. Ларина)
a) Решите уравнение 
б) Укажите корни уравнения, принадлежащие отрезку Решение
31. (Т/Р А. Ларина)
a) Решите уравнение 
б) Укажите корни уравнения, принадлежащие интервалу 
Решение
32. (Т/Р А. Ларина)
a) Решите уравнение 
б) Укажите корни, принадлежащие отрезку 
Решение
33. (Т/Р А. Ларина)
a) Решите уравнение 
б) Укажите его корни, принадлежащие отрезку Решение
34. (Т/Р А. Ларина)
а) Решите уравнение 
б) Укажите его корни из отрезка 
Решение
35. (Т/Р А. Ларина)
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение
36. (Т/Р А. Ларина)
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие промежутку 
Решение
37. (Т/Р А. Ларина)
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение
38. (Т/Р А. Ларина)
а) Решите уравнение 
б) Найдите его корни на отрезке 
Решение
39. (Т/Р А. Ларина)
а) Решите уравнение 
б) Найдите его корни на отрезке 
Решение
40. (Т/Р А. Ларина)
а) Решите уравнение 
б) Найдите его корни, принадлежащие промежутку 
Решение
41. (Т/Р А. Ларина)
a) Решите уравнение 
б) Найдите его корни, принадлежащие промежутку Решение
42. (Т/Р А. Ларина)
а) Решите уравнение 
.
б) Найдите его корни, принадлежащие промежутку 
Решение
43. (Т/Р А. Ларина)
a) Решите уравнение 
б) Найдите его корни, принадлежащие отрезку Решение
44. (Т/Р А. Ларина)
а) Решите уравнение 
.
б) Найдите его корни, принадлежащие промежутку 
Решение
45. (Т/Р А. Ларина)
а) Решите уравнение 
.
б) Укажите корни этого уравнения, принадлежащие отрезку 
. Решение
46. (Т/Р А. Ларина)
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие промежутку 
Решение
47. (Т/Р А. Ларина)
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
48. (Т/Р А. Ларина)
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие интервалу 
Решение
49. (Т/Р А. Ларина)
a) Решите уравнение 
.
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение
50. (Т/Р А. Ларина)
а) Решите уравнение 
.
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение
51. (Т/Р А. Ларина)
a) Решите уравнение 
б) Найдите его корни, принадлежащие отрезку 
Решение
52. (Т/Р А. Ларина)
а) Решите уравнение 
б) Найдите его корни, принадлежащие отрезку 
Решение
53. (Т/Р А. Ларина)
а) Решите уравнение 
б) Укажите корни уравнения, принадлежащие отрезку 
. Решение
54. (Т/Р А. Ларина)
a) Решите уравнение 
б) Найдите его корни, принадлежащие отрезку Решение
55. (Т/Р А. Ларина)
a) Решите уравнение 
б) Найдите его корни, принадлежащие отрезку 
Решение
56. (Т/Р А. Ларина)
а) Решите уравнение 
б) Укажите его корни из интервала 
Решение
57. (Т/Р А. Ларина)
а) Решите уравнение 
б) Укажите его корни, принадлежащие интервалу 
Решение
58. (Т/Р А. Ларина)
a) Решите уравнение 
.
б) Укажите корни, принадлежащие отрезку Решение
59. (Т/Р А. Ларина)
a) Решите уравнение 
.
б) Укажите корни, принадлежащие отрезку 
Решение
60. (Т/Р А. Ларина)
a) Решите уравнение 
б) Найдите все корни на промежутке 
Решение
61. (Т/Р А. Ларина)
a) Решите уравнение 
б) Укажите корни, принадлежащие отрезку 
Решение
62. (Т/Р А. Ларина)
a) Решите уравнение 
б) Укажите корни уравнения, принадлежащие интервалу 
Решение
63. (Т/Р А. Ларина)
a) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие интервалу 
Решение
64. (Т/Р А. Ларина)
а) Решите уравнение 
.
б) Найдите все корни уравнения на отрезке 
Решение
65. (Т/Р А. Ларина)
а) Решите уравнение 
б) Найдите все корни уравнения на отрезке [− 3;2]. Решение
66. (Т/Р А. Ларина)
а) Решите уравнение 
б) Найдите все корни на промежутке (0; 5). Решение
67. (Т/Р А. Ларина)
а) Решите уравнение 
б) Найдите все корни на промежутке 
. Решение
68. (Т/Р А. Ларина)
а) Решите уравнение 
.
б) Найдите все корни на промежутке 
Решение
69. (Т/Р А. Ларина)
a) Решите уравнение 
,
б) Найдите все корни на промежутке 
. Решение
70. (Т/Р А. Ларина)
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие промежутку 
. Решение
71. (Т/Р А. Ларина)
Дано уравнение 
а) Решите уравнение.
б) Укажите корни этого уравнения, принадлежащие промежутку 
. Решение
72. (Т/Р А. Ларина)
Дано уравнение 
а) Решите уравнение.
б) Укажите его корни из отрезка 
. Решение
73. (Т/Р А. Ларина)
Дано уравнение 
а) Решите уравнение.
б) Укажите его корни из отрезка . Решение
74. (Т/Р А. Ларина)
Дано уравнение 
а) Решите уравнение.
б) Укажите его корни из интервала 
. Решение
75. (Т/Р А. Ларина)
Дано уравнение 
а) Решите уравнение.
б) Укажите его корни из отрезка . Решение
76. (Т/Р А. Ларина)
Дано уравнение 
а) Решите уравнение.
б) Укажите его корни из отрезка . Решение
77. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Укажите его корни из отрезка 
. Решение
78. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Укажите его корни из отрезка 
. Решение
79. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Укажите его корни из отрезка 
. Решение
80. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Укажите его корни из отрезка 
. Решение
81. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Найдите наибольший отрицательный корень. Решение
82. (Т/Р, 2017) а) Решите уравнение 
б) Найдите все его корни, принадлежащие отрезку 
Решение
83. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Найдите решения, принадлежащие промежутку 
. Решение
84. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Найдите натуральное число 
такое, что 
где 
– корень уравнения. Решение
85. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку 
. Решение
86. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку 
. Решение
87. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку 
. Решение
88. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку 
. Решение
89. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку 
. Решение
90. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку 
. Решение
91. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку 
. Решение
92. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку 
.
93. (Т/Р А. Ларина)
Дано уравнение 
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку 
. Решение
94. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку 
. Решение
95. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку 
. Решение
96. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку 
. Решение
97. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку 
.
98. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку 
. Решение
99. (Т/Р А. Ларина) Дано уравнение 
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку 
. Решение
100. (Т/Р 283 А. Ларина) a) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение
Видео:Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать
Задание №13 ЕГЭ по математике профильного уровня
Видео:ЕГЭ Математика Задание 12 #519423Скачать
Уравнения
В 13 задании профильного уровня ЕГЭ по математике необходимо решить уравнение, но уже повышенного уровня сложности, так как с 13 задания начинаются задания бывшего уровня С, и данное задание можно назвать С1. Перейдем к рассмотрению примеров типовых заданий.
Разбор типовых вариантов заданий №13 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант2018)
Алгоритм решения:
- При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем
Простейшие (Protozoa) — тип одноклеточных животных.
- Строим числовую ось.
- Наносим на нее корни.
- Отмечаем концы отрезка.
- Выбираем те значения, которые лежат внутри промежутка.
- Записываем ответ.
Решение:
сos2x = 1 – sin x.
Преобразуем левую часть уравнения, используя формулу косинуса двойного аргумента, с использованием синуса:
Получаем такое уравнение: 1−sin 2 x=1− sinx Теперь в уравнении присутствует только одна тригонометрическая функция sinx. 2. Вводим замену: t = sinx. Решаем получившееся квадратное уравнение:
3. Делаем обратную замену:
Решаем эти уравнения:
Следовательно, получаем два семейства решений. Пункт б):
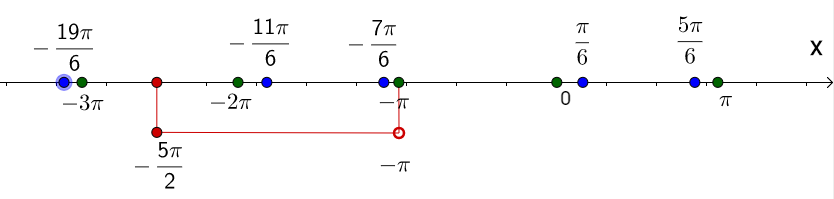
1. В предыдущем пункте получено два семейства, в каждом из которых бесконечно много решений. Необходимо выяснить, какие из них, находятся в заданном промежутке. Для этого строим числовую прямую.
2. Наносим на нее корни обоих семейств, пометив их зеленым цветом (первого) и синим (второго).
3. Красным цветом помечаем концы промежутка. 4. В указанном промежутке расположены три
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Второй вариант задания (из Ященко, №1)
Алгоритм решения:
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем простейшие показательные, потом тригонометрические уравнения.
- Строим координатную плоскость и окружность единичного радиуса на ней.
- Отмечаем точки, являющиеся концами отрезка.
- Выбираем те значения, которые лежат внутри отрезка.
- Записываем ответ.
Решение:
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
D=b 2 – c = 81 – 4∙4∙2 =49,
3. Возвращаемся к переменной х: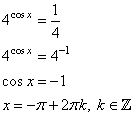 
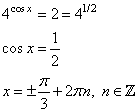
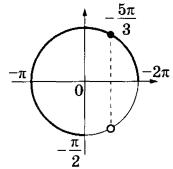
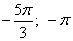
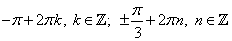
Пункт б) 1. Строим координатную плоскость и окружность единичного радиуса на ней. 2. Отмечаем точки, являющиеся концами отрезка. 3. Выбираем те значения, которые лежат внутри отрезка.. 
Это корни 
. Их два. Ответ: а) 
б) 
Третий вариант задания (из Ященко, № 6)
Алгоритм решения:
- При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем простейшие показательные, а затем тригонометрические уравнения.
- Решаем неравенства для каждого случая.
- Записываем ответ.
💥 Видео
Задание 12 ЕГЭ профиль Логарифмическое уравнениеСкачать
а) Решите уравнение (x-2)^2/2+18/(x-2)^2=7((x-2)/2-3/(x-2))+10. б) Найдите его корни, принадлежащиеСкачать
Отбор корней по окружностиСкачать
Три способа отбора корней в задании 13 ЕГЭ профильСкачать
ЕГЭ по математике // Профильный уровень // Задание 13 (C1) // Рациональное уравнениеСкачать
КОГДА ПИСАТЬ +Пк, а когда +2Пк? (Задание 13 по Тригонометрии ЕГЭ 2024 по Математике Профиль)Скачать
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать
Профильный ЕГЭ 2022. Сложные уравнения. Задание 12Скачать
Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать
Отбор корней с аркфункциями в №12 | Это будет на ЕГЭ 2023 по математикеСкачать
ЕГЭ Математика Задание 12 #507572Скачать
Решаем интересные №12 из нового сборника Ященко ЕГЭ 2023 по математикеСкачать
ЕГЭ Математика Задание 12 #521850Скачать
2 часть ЕГЭ Рациональные уравнения / разбор задания #519426Скачать
2 часть ЕГЭ Рациональные уравнения / разбор задания 563297Скачать
Математика ЕГЭ. Тригонометрия. Сложный приемСкачать
ЕГЭ математика. 13 задание. Рациональное уравнениеСкачать
