Задачи с углами для 5 класса углы с уравнениями

Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Вариант 1.

1. Решите задачу:

Витя прочитал 100 страниц из книги, при этом ему осталось прочитать в 1,5 раза больше. Сколько процентов книги прочел Витя? Сколько процентов ему осталось проесть?

Решение
• 1) 100 * 1,5 = 150 (стр.) осталось прочесть Вите;
• 2) 100 + 150 = 250 (стр.) вся книга;
• 3) 100 : 250 * 100 = 40%;
• 4) 100 — 40 = 60%.
• Ответ: Витя прочел 40% кнгиги, ему осталось прочесть 60% книги.

2. Решите задачу:

Стоимость книги, сначала увеличили на 20%, а потом снизили на 15 рублей. Сколько стоила книга сначала, если теперь она стоит 225 рублей?

Решение
• 1) 225 + 15 = 240 (рублей) стоимость книги до снижения стоимости;
• Пусть книга стоила x рублей, тогда 20% от x равно 0,2x.
• x + 0,2x = 240;
• 1,2x = 240;
• x = 240 : 1,2;
• x = 200;
• Ответ: сначала книга стоила 200 рублей.

3. Выполните задание:

В треугольнике ABC угол ∠A равен 48°, угол ∠B равен 32°. Постройте треугольник ABC. Чему равен угол ∠C? Чему равна сумма всех углов треугольника?

Решение
• Сумма всех углов треугольника равна 180°
• 1) 48 + 32 = 80° сумма углов ∠A и ∠B;
• 2) 180 — 80 = 100°;
• Ответ: угол ∠C = 100°. Сумма всех углов треугольника равна 180°.

4. Решите задачу:

Угол ∠BOD = 152°, ∠COD = 55°, угол ∠AOD — развернутый. Найдите величины остальных углов изображенных на рисунке.

Решение
• 1) 152 — 55 = 97°;
• 2) 180 — 152 = 28°;
• Ответ: угол ∠BOC = 97°, угол ∠AOB = 28°.

5. Логическая задача:

Пенсию дедушки увеличили на 50%, а пенсию бабушки на 60%. Означает ли это, что бабушка получит большую прибавку к пенсии?

Видео:Угол. Градусная мера угла. Практическая часть - решение задачи. 5 класс.Скачать

Вариант 2.

1. Решите задачу:

В магазине до обеда было продано 60 кг муки, а осталось в 1,5 раза больше, чем продано. Сколько процентов всей муки было продано до обеда? Сколько процентов муки осталось в магазине?

Решение
• 1) 60 * 1,5 = 90 (кг) муки осталось;
• 2) 60 + 90 = 150 (кг) всего муки;
• 3) 60 : 150 * 100 = 40%;
• 4) 100 — 40 = 60%.
• Ответ: до обеда продали 40% муки, осталось 60%.

2. Решите задачу:

Благодаря оптимизации производственного процесса, себестоимость одной единицы продукции уменьшилась на 25%, а потом еще на 10 рублей. Какова была начальная себестоимость продукции, если сейчас она составляет 170 рублей?

Решение
• 1) 170 + 10 = 180 (рублей) себестоимость продукции до второго снижения;
• Пусть себестоимость продукции сначала была равна x, тогда 25% от ее себестоимости 0,4x;
• x — 0,4x = 180;
• 0,6x = 180;
• x = 180 : 0,6;
• x = 300;
• Ответ: начальная себестоимость одной единицы продукции 300 — рублей.

3. Выполните задание:

У треугольника AOD угол ∠A = 60° угол ∠O = 42°. Постройте треугольник AOD. Чему равен угол ∠D? Чему равна сумма всех углов треугольника?

Решение
• Сумма всех углов треугольника равна 180°;
• 1) 60 + 42 = 102°; сумма углов ∠A и O∠;
• 2) 180° — 102° = 78°.
• Ответ: ∠D равен 78°. Сумма всех углов треугольника равна 180°.

4. Решите задачу:

Угол ∠BOD = 110°, ∠COD= 33°, угол ∠AOD — развернутый. Найдите величины остальных углов изображенных на рисунке.

Решение
• 1) 110° — 33° = 77°;
• 2) 180° — 110° = 70°;
• Ответ: угол ∠BOC = 77° угол ∠AOB = 70°.

5. Логическая задача:

Стоимость тетради увеличилась на 20%, а стоимость альбома увеличилась на 15%. Означает ли это, что надбавка на стоимость тетради больше, чем на стоимость альбома?

Видео:Математика 5 класс (Урок№27 - Углы. Измерение углов.)Скачать

Теоретические и практические задания для уроков по теме: «Углы. Измерение углов» (5 класс)
методическая разработка по математике (5 класс) на тему

Предложенный материал может быть использован на уроках математики в 5 классе по теме «Углы. Измерение углов.» Материал разработан в соответствии с содержанием учебника «Математика 5» авторов С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин.

Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Скачать:

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Видео:Смежные и вертикальные углы. Практическая часть - решение задачи. 7 класс.Скачать

Предварительный просмотр:

Углы. Измерение углов.

Прочитав текст, расположенный ниже, ответь на вопросы:

1. какой прибор служит для измерения углов в градусах?
2. перечислите по порядку действия, которые надо произвести, чтобы измерить в градусах величину угла.

Для измерения углов в градусах служит прибор, который называется транспортиром. (см. рис. 10) .

Алгоритм измерения углов.

1. Совместить вершину угла с центром транспортира.

1. Расположить транспортир так, чтобы одна из сторон угла проходитла через начало отсчета на шкале транспортира (совместить с 0 0 )

1. Найти штрих на шкале, через который проходит вторая сторона угла.

1. Проверить соответствует ли мера угла его виду.

1. Перепиши алгоритм измерения углов в тетрадь.

2. Выполни задания № 423, 424. 426, 427

Видео:ЗАДАЧИ НА НАХОЖДЕНИЕ УГЛОВ. Задача №1. Примеры | МАТЕМАТИКА 5 классСкачать

Предварительный просмотр:

Углы. Измерение углов.

Прочитав текст, расположенный ниже, ответь на вопросы:

1. Сформулируйте и запиши алгоритм построения угла заданной величины.

1. Сформулируйте свой план построения угла данной величины, например план построения угла в 40 0 . Проведите построение по составленному плану.

2. Сравните сформулированный план построения угла с алгоритмом построения угла заданной величины, приведенным ниже.

Алгоритм построения угла (рис. 11):

1. Начертить луч.
2. Совместить центр транспортира с началом луча так, чтобы луч проходил через начало отсчёта на шкале транспортира.
3. Найти на нужном ряду необходимое значение угла и поставить на бумаге точку.
4. Соединить начало луча с отмеченной точкой.
5. Проверить вид угла, который нужно построить. Искомый угол построен.

3. Перепишите алгоритм построения угла в тетрадь.

1. № 425 учебника.

2. Начертите угол в 130 0 . затем начертите угол, который:

1) на 55 0 меньше данного угла;

2) в 2 раза меньше данного угла.

3. начертите угол АОВ, равный 30 0 . затем начертите угол который:

Видео:Задачи: смежные и вертикальные углы. 4 задачи за 7 минут. Все о смежных и вертикальных углахСкачать

Выборка заданий по математике. ОГЭ. 5 класс. Углы. Виды углов. Биссектриса. ФИПИ.РешуОГЭ.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Блок 6. Подборка заданий для учащихся 5 класс. Углы. Виды углов. Биссектриса. Источник ФИПИ, РешуОГЭ.

1. Найдите величину угла DOK , если OK — биссектриса угла AOD , ∠ DOB = 108°. Ответ дайте в градусах.

2. Найдите величину угла DOK , если OK — биссектриса угла AOD , ∠ DOB = 64°. Ответ дайте в градусах.

3. Найдите величину угла DOK , если OK — биссектриса угла AOD , ∠ DOB = 52°. Ответ дайте в градусах.

4. Найдите величину угла AOK , если OK — биссектриса угла AOD , ∠ DOB = 64°. Ответ дайте в градусах.

5. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 44°. Найдите угол CMA . Ответ дайте в градусах.

6. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 48°. Найдите угол CMA . Ответ дайте в градусах.

7. На прямой взята точка . Луч — биссектриса угла . Известно, что . Найдите угол . Ответ дайте в градусах.

8. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 57°. Найдите угол CMA . Ответ дайте в градусах.

9. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 39°. Найдите угол CMA . Ответ дайте в градусах.

10. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 24°. Найдите угол CMA . Ответ дайте в градусах.

11. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 64°. Найдите угол CMA . Ответ дайте в градусах.

12. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 44°. Найдите угол CMA . Ответ дайте в градусах.

13. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 72°. Найдите угол CMA . Ответ дайте в градусах.

14. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 41°. Найдите угол CMA . Ответ дайте в градусах.

15. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 74°. Найдите угол CMA . Ответ дайте в градусах.

16. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 65°. Найдите угол CMA . Ответ дайте в градусах.

17. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 28°. Найдите угол CMA . Ответ дайте в градусах.

18. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 81°. Найдите угол CMA . Ответ дайте в градусах.

19. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 67°. Найдите угол CMA . Ответ дайте в градусах

.

20. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 29°. Найдите угол CMA . Ответ дайте в градусах.

21. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 60°. Найдите угол CMA . Ответ дайте в градусах.

23. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 52°. Найдите угол CMA . Ответ дайте в градусах.

24. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 78°. Найдите угол CMA . Ответ дайте в градусах.

25. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 16°. Найдите угол CMA . Ответ дайте в градусах.

26. На прямой AB взята точка M . Луч MD — биссектриса угла CMB . Известно, что ∠ DMC = 18°. Найдите угол CMA . Ответ дайте в градусах.

27. Найдите величину угла AOK , если OK — биссектриса угла AOD , ∠ DOB = 52°. Ответ дайте в градусах.

1. В треугольнике известно, что , — биссектриса. Найдите угол . Ответ дайте в градусах.

2. В треугольнике известно, что , — биссектриса. Найдите угол . Ответ дайте в градусах.

3. В треугольнике известно, что , — биссектриса. Найдите угол . Ответ дайте в градусах.

4. В треугольнике известно, что , — биссектриса. Найдите угол . Ответ дайте в градусах.

5. В треугольнике ABC известно, что ∠ BAC =82°, AD — биссектриса. Найдите угол BAD . Ответ дайте в градусах.

6. В треугольнике ABC известно, что ∠ BAC =62°, AD — биссектриса. Найдите угол BAD . Ответ дайте в градусах.

7. В треугольнике ABC известно, что ∠ BAC =42°, AD — биссектриса. Найдите угол BAD . Ответ дайте в градусах.

8. В треугольнике ABC известно, что ∠ BAC =84°, AD — биссектриса. Найдите угол BAD . Ответ дайте в градусах.

9. В треугольнике ABC известно, что ∠ BAC =86°, AD — биссектриса. Найдите угол BAD . Ответ дайте в градусах.

10. В треугольнике ABC известно, что ∠ BAC =64°, AD — биссектриса. Найдите угол BAD . Ответ дайте в градусах.

11. В треугольнике ABC известно, что ∠ BAC =68°, AD — биссектриса. Найдите угол BAD . Ответ дайте в градусах.

12. В треугольнике ABC известно, что ∠ BAC =46°, AD — биссектриса. Найдите угол BAD . Ответ дайте в градусах.

13. В треугольнике ABC известно, что ∠ BAC =48°, AD — биссектриса. Найдите угол BAD . Ответ дайте в градусах.

14. В треугольнике ABC известно, что ∠ BAC =24°, AD — биссектриса. Найдите угол BAD . Ответ дайте в градусах.

15. В треугольнике ABC известно, что ∠ BAC =26°, AD — биссектриса. Найдите угол BAD . Ответ дайте в градусах.

16. В треугольнике ABC известно, что ∠ BAC =28°, AD — биссектриса. Найдите угол BAD . Ответ дайте в градусах.

🎬 Видео

Угол. Градусная мера угла. 5 класс.Скачать

Тема 20. Угол. Измерение и построение углов. Решение задачСкачать

КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

Урок 14 Решение задач с помощью уравнений (5 класс)Скачать

Разбор 31 варианта ОГЭ по математике 2024 / ПДФ решение + формулы / МатТаймСкачать

5 класс. УглыСкачать

Угол. Практическая часть - решение задачи. 7 класс.Скачать

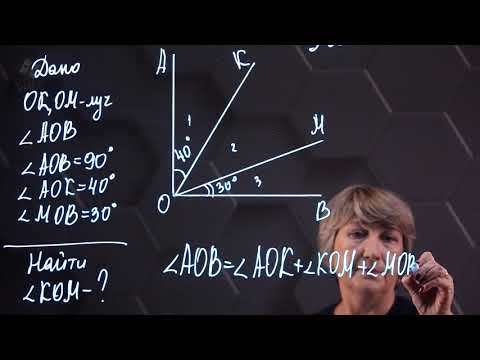
Транспортир. Измерение и построение углов. 5 класс.Скачать

Как думаешь, пятиклассник решит задачу с углами? #математика #геометрия #угол #уравнение #системаСкачать

Сравнение углов. Виды углов. Чертежный треугольник. 5 класс.Скачать

Уравнение. Практическая часть - решение задачи. 1 часть. 5 класс.Скачать

Виды углов. Измерение углов. 5 классСкачать

5 класс, 42 урок, Измерение углов. ТранспортирСкачать