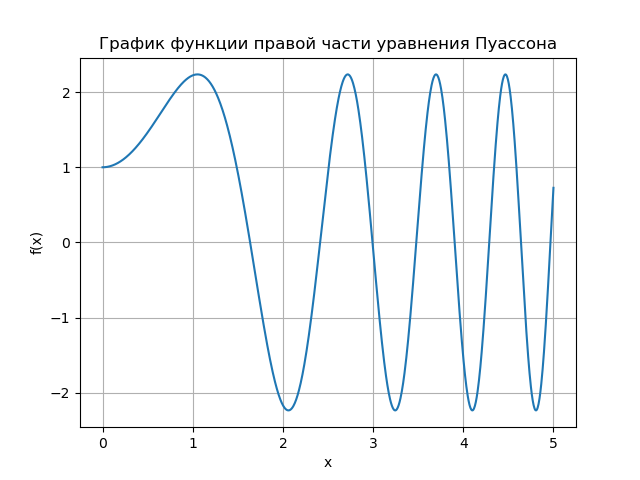
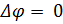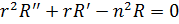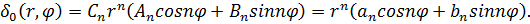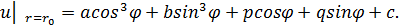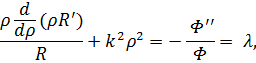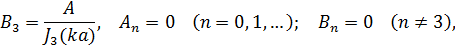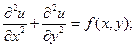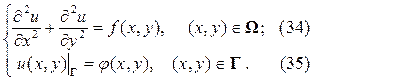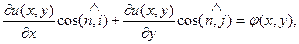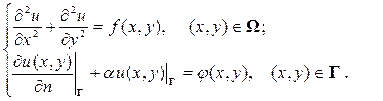Введение
Наиболее распространённым уравнением эллиптического типа является уравнение Пуассона.
К решению этого уравнения сводятся многие задачи математической физики, например задачи о стационарном распределении температуры в твердом теле, задачи диффузии, задачи о распределении электростатического поля в непроводящей среде при наличии электрических зарядов и многие другие.
Для решения эллиптических уравнений в случае нескольких измерений используют численные методы, позволяющие преобразовать дифференциальные уравнения или их системы в системы алгебраических уравнений. Точность решения определяется шагом координатной сетки, количеством итераций и разрядной сеткой компьютера [1]
Цель публикации получить решение уравнения Пуассона для граничных условий Дирихле и Неймана, исследовать сходимость релаксационного метода решения на примерах.
Уравнение Пуассона относится к уравнениям эллиптического типа и в одномерном случае имеет вид [1]:
(1)
где x – координата; u(x) – искомая функция; A(x), f(x) – некоторые непрерывные функции координаты.
Решим одномерное уравнение Пуассона для случая А = 1, которое при этом принимает вид:
(2)
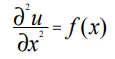
Зададим на отрезке [xmin, xmax] равномерную координатную сетку с шагом ∆х:
(3)
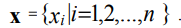
Граничные условия первого рода (условия Дирихле) для рассматриваемой задачи могут быть представлены в виде:
(4)
где х1, xn – координаты граничных точек области [xmin, xmax]; g1, g2 – некоторые
константы.
Граничные условия второго рода (условия Неймана) для рассматриваемой задачи могут быть представлены в виде:
(5)
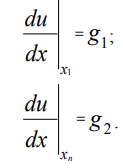
Проводя дискретизацию граничных условий Дирихле на равномерной координатной сетке (3) с использованием метода конечных разностей, получим:
(6)
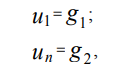
где u1, un – значения функции u(x) в точках x1, xn соответственно.
Проводя дискретизацию граничных условий Неймана на сетке (3), получим:
(7)
Проводя дискретизацию уравнения (2) для внутренних точек сетки, получим:
(8)
где ui, fi – значения функций u(x), f(x) в точке сетки с координатой xi.
Таким образом, в результате дискретизации получим систему линейных алгебраических уравнений размерностью n, содержащую n – 2 уравнения вида (8) для внутренних точек области и уравнения (6) и (7) для двух граничных точек [1].
Ниже приведен листинг на Python численного решения уравнения (2) с граничными условиями (4) – (5) на координатной сетке (3).
Разработанная мною на Python программа удобна для анализа граничных условий.Приведенный алгоритм решения на Python использует функцию Numpy — u=linalg.solve(a,b.T).T для решения системы алгебраических уравнений, что повышает быстродействие при квадратной матрице . Однако при росте числа измерений необходимо переходить к использованию трех диагональной матрицы решение для которой усложняется даже для очень простой задачи, вот нашёл на форуме такой пример:
Программа численного решения на равномерной по каждому направлению сетки задачи Дирихле для уравнения конвекции-диффузии
(9)
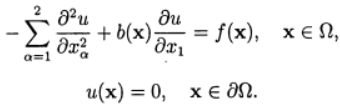
Используем аппроксимации центральными разностями для конвективного слагаемого и итерационный метод релаксации.для зависимость скорости сходимости от параметра релаксации при численном решении задачи с /(х) = 1 и 6(х) = 0,10. В сеточной задаче:
(10)
Представим матрицу А в виде суммы диагональной, нижней треугольной и верхней треугольных матриц:
(10)
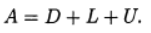
Метод релаксации соответствует использованию итерационного метода:
(11)
При 
говорят о верхней релаксации, при 
— о нижней релаксации.
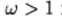
На графике показана зависимость числа итераций от параметра релаксации для уравнения Пуассона (b(х) = 0) и уравнения конвекции-диффузии (b(х) = 10). Для сеточного уравнения Пуассона оптимальное значении параметра релаксации находится аналитически, а итерационный метод сходиться при 
.
- Приведено решение эллиптической задачи на Python с гибкой системой установки граничных условий
- Показано что метод релаксации имеет оптимальный диапазон (
) параметра релаксации.
Ссылки:
- Рындин Е.А. Методы решения задач математической физики. – Таганрог:
Изд-во ТРТУ, 2003. – 120 с. - Вабищевич П.Н.Численные методы: Вычислительный практикум. — М.: Книжный дом
«ЛИБРОКОМ», 2010. — 320 с.
Видео:Решение биквадратных уравнений. 8 класс.Скачать
ТЕМА: Уравнения эллиптического типа
ТИТУЛЬНЫЙ ЛИСТ
1 Теоретические обоснования уравнений эллиптического типа………………. 4
1.1. Задачи приводящие к уравнению Лапласа………………. 5
1.2. Уравнение Шредингера и его стационарный аналог. 9
1.3. Уравнение Гельмгольца……………………………………………. ……10
2 Примеры решения задач на уравнения эллиптического типа……………………12
Список использованных источников……………………………………………. …16
В курсовой работе будут рассмотрены уравнения эллиптического типа.
Актуальность исследования заключается в том, что благодаря данному типу уравнений можно описать стационарные процессы, проходящие в различных физических полях. Например, с помощью уравнения Пуассона можно описать электростатическое поле, поле давления [1].
Исследование затронет следующие проблемы: применение уравнений эллиптического типа на практике и способы их решения.
Целью исследования является: изучение вопроса, касающегося применения уравнений эллиптического типа на практике.
Основными задачами, поставленными для достижения цели можно считать:
— ознакомиться с положениями, характеризующими уравнения эллиптического типа;
— выявить основные уравнения, относящиеся к данному типу;
— освоить навык решения задач, используя данные уравнения;
— показать специфику проблем, которые могут возникнуть на этапах решения.
Объектом исследования заданной темы являются дифференциальные уравнения в частных производных.
Предметом исследования выступают уравнения эллиптического типа.
Теоретической и методологической основой исследования послужили труды отечественных и зарубежных деятелей, методические пособия по дисциплине «методы математической физики».
1. ТЕОРЕТИЧЕСКИЕ ОБОСНОВАНИЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
Помимо физических явлений, развивающихся в пространстве и во времени, существует множество процессов, которые не изменяются с течением времени. Эти процессы называются стационарными. При исследовании данных процессов, различной физической природы (колебания, теплопроводность, диффузия и др.) обычно приходят к уравнениям эллиптического типа. Примерами могут выступать:
1. Уравнения Лапласа и Пуассона, описывают различные стационарные физические поля.
2. Стационарный аналог уравнения Шредингера, когда предполагается гармоническая зависимость от времени.
3. Уравнение Гельмгольца.
4. Уравнения, получаемые из уравнения Максвелла, если предполагается, что электромагнитное поле не изменяется с течением времени [1].
Наиболее распространенным уравнением этого типа является уравнение Лапласа
.
Этим уравнением характеризуется гравитационный и электростатический потенциалы в точках свободного пространства, оно описывает потенциал скорости безвихревого потока несжимаемой жидкости, и оно же справедливо для температуры однородной изотропной среды при установившемся движении тепла.
Функция 
называется гармонической в области 
, если она непрерывна в этой области вместе со своими производными до 2-го порядка и удовлетворяют уравнению Лапласа.
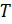
При изучении свойств гармонических функций были разработанные различные математические методы, оказавшиеся плодотворными и в применении к уравнениями гиперболического и параболического типов [1].
1.1. ЗАДАЧИ ПРИВОДЯЩИЕ К УРАВНЕНИЮ ЛАПЛАСА
1. Стационарное тепловое поле. Постановка краевых задач.
Рассматривается стационарное тепловое поле. Температура нестационарного теплового может быть представлена дифференциальным уравнением теплопроводности
Если процесс стационарен, то устанавливается распределение температуры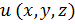 
, не меняющееся с течением времени и, следовательно, удовлетворяющее уравнению Лапласа
 | (1) |
При наличии источников тепла получается уравнение
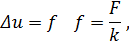 | (2) |
где 
– плотность тепловых источников, а 
– коэффициент теплопроводности. Неоднородное уравнение Лапласа (2) часто называют уравнением Пуассона.
Рассматривается некоторый объем 
, ограниченный поверхностью 
. Задача о стационарном распределении температуры внутри тела 
формулируется следующим образом:
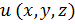
Найти функцию 
, удовлетворяющую внутри Т уравнению
 , | (3) |
и граничному условию, которое может быть взято в одном из следующих видов:
I. 
на 
(первая краевая задача);
II. 
на 
(вторая краевая задача);
III. 
на 
(третья краевая задача).
где 
, 
, 
, 
— заданные функции, 
– производная по внешней нормали к поверхности
Первую краевую задачу называют для уравнений Лапласа часто называют задачей Дирехле, а вторую задачу – задачей Неймана.
Если ищется решение в области 
, внутренней (или внешней) по отношению к поверхности 
, то соответствующую задачу называют внутренней (или внешней) краевой задачей [3].
2. Потенциальное течение жидкости. Потенциал стационарного тока и электростатического поля.
В качестве второго примера будет рассмотрено потенциальное течение жидкости без источников. Пусть внутри некоторого объема 
с границей 
имеет место стационарное течение несжимаемой жидкости (плотность 
), характеризуемое скоростью 
. Если течение жидкости не вихревое, то скорость 
является потенциальным вектором, т.е
 | (4) |
где 
– скалярная функция, называемая потенциалом скорости. Если отсутствуют источники, то
 . | (5) |
При подстановке сюда выражения (3) для υ, выходит:
,
 , | (6) |
то есть потенциал скорости удовлетворяет уравнению Лапласа.
Пусть в однородной проводящей среде имеется стационарный ток с объемной плотностью 
. Если в среде нет объемных источников тока, то
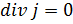 . | (7) |
Электрическое поле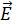 
определяется через плотность тока из дифференциального закона Ома
 | (8) |
где 
– проводимость среды.
Поскольку процесс стационарный, то электрическое поле является безвихревым или потенциальным, т.е. существует такая скалярная функция 
для которой
  ). | (9) |
Отсюда на основании формул (6) и (7) заключается, что
| , | (10) |
т.е. потенциал электрического поля стационарного тока удовлетворяет уравнению Лапласа.
Рассматривается электрическое поле стационарных зарядов. Из стационарности процесса следует, что
 , | (11) |
т.е. поле является потенциальным и
 . |
Пусть 
– объемная плотность заряда, имеющихся в среде, характеризуемой диэлектрической постоянной 
.
Исходя из основного закона электродинамики
 | (12) |
где – некоторый объем, 
– поверхность, его ограничивающая, где 
– сумма всех зарядов внутри , и пользуясь теоремой Отроградского
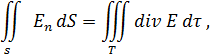 | (13) |
.
При подстановке сюда выражение (8) для 
, выходит:
 , | (14) |
т.е. электростатический потенциал 
удовлетворяет уравнению Пуассона. Если объемных зарядов нет 
, то потенциал должен удовлетворять уравнению Лапласа
Нами был рассмотрен ряд процессов. Основные краевые задачи для которых относятся к трем типам, приведенным выше [1].
1.2. УРАВНЕНИЕ ШРЕДИНГЕРА И ЕГО СТАЦИОНАРНЫЙ АНАЛОГ
В квантовой механике состояние частицы описывается волновой функцией 
, квадрат модуля которой имеет смысл плотности вероятности найти частицу в окрестности данной точки 
в момент времени 
[2]. Волновая функция удовлетворяет уравнению Шредингера
где 
— постоянная Планка. Оператор Гамильтона 
для движения частицы в поле 
имеет вид
Уравнение Шредингера является уравнением в частных производных второго порядка по координатам, но первого порядка по времени. В отличие от волнового уравнения, чтобы выделить частное решение из общего, надо задавать при 
одно начальное условие, а не два.
Если искать решение в виде стационарных состояний 
, имеющих определенную энергию 
, то время можно исключить и получить стационарное уравнение Шредингера
 | (15) |
Требуется найти не только решение 
, но и такие значения энергии , при которых эти решения удовлетворяют граничным условиям. Такая постановка называется спектральной задачей [3].
1.3 УРАВНЕНИЕ ГЕЛЬМГОЛЬЦА
Эллиптическое дифференциальное уравнение в частных производных, получаемое из уравнение Максвелла, если предполагается, что электромагнитное поле либо не меняется с течением времени, либо меняется по гармоническому закону. Может быть представлено как
где 
– это оператор Лапласа, а неизвестная функция 
определена в 
(на практике уравнение Гельмгольца применяется для 
).
В уравнение Гельмгольца не входят операторы дифференцирования по времени, следовательно, сведение исходной задачи в частных производных к уравнению Гельмгольца может упростить её решение. Для примера рассматривается волновое уравнение:
 | (16) |
Пусть функции 
и 
допускают разделение переменных: 
, и пусть 
. Нужно заметить, что в пространстве Фурье – преобразований дифференцирование по времени соответствует умножению на множитель 
. Таким образом, уравнение приводится к виду:
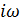
 | (17) |
где 
= 
— это квадрат модуля волнового вектора.
Решение уравнения Гельмгольца зависит от вида граничных условий. В двумерном случае уравнение Гельмгольца применяется для решения задачи о колеблющейся мембране, тогда естественным образом задаются однородные граничные условия, что физически соответствует закреплению мембраны на границе. В таком случае решение будет зависеть от формы мембраны. Так, для круглой мембраны радиуса 
в полярных координатах 
уравнение принимает вид:
 | (18) |
Метод разделения переменных позволяет перейти к задаче на собственные значения для части решения, зависящей только от 
:
 | (19) |
 | (20) |
а функция, зависящая только от радиуса, будет удовлетворять уравнению:
 | (21) |
Фундаментальными решениями этих уравнений являются, соответственно, функции 
, где 
– i-корень функции Бесселя λ-го порядка [4].
2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
В отличие от смешанных задач, для эллиптических уравнений ставится только краевая задача
где 
– внешняя нормаль к границе области 
.
При этом, если 
, задача называется задачей Дирихле, если 
, задачей Неймана, если 
то задача называется смешанной.
Задачи буду решаться в полярных или сферических координатах. Заданные краевые условия произвольные, неоднородные. Однородные краевые условия для нахождения собственных функций возникают из-за того, что области имеют специальный вид, а потому решение должно иметь период 
, а в случае 
прибавляются условия 
(уравнение Лапласа в новых координатах при этом имеет особенность). [5].
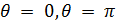
Предлагаю рассмотреть метод нахождения решения уравнения Лапласа в круге, то есть метод нахождения функции 
, удовлетворяющий уравнению Лапласа внутри круга радиусом 
c центром в полюсе полярной системы координат и граничному условию на окружности
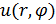
где 
– заданная функция, непрерывная на окружности.
Задача № 1. Решить краевую задачу для уравнения 
в круге 
, если на границе круга 
φ.
Решение: Уравнение Лапласа в полярных координатах имеет вид
 | (22) |
1. Частное решение уравнения в соответствии с методом Фурье ищется в виде
причем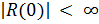 
и 
периодическая с периодом 
При подстановке 
в уравнение (22) и разделяя переменные, выходит
Поэтому функции 
и являются решениями связанных задач:
a) 
b) 
2. Решается задача 
Общее решение уравнения 
имеет вид
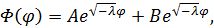 | (23) |
где 
и 
– константы.
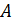
Это решение периодично при 
и имеет период 
при
Если 
Если 
3. Решается задача 
Если 
Общее решение этого уравнения
Так как 
Если 
, 
Общее решение этого уравнения
Так как 
4. Вспомогательные решения имеют вид:
5. Тогда решение исходной задачи ищется в виде
6. При использовании граничного условия 
sin3φ,
получается 
sin3φ. Отсюда
В результате
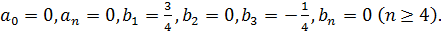
Ответ:
Задача № 2. Решить краевую задачу 
Решение: Проводятся преобразования, аналогичные предыдущей задачи до момента нахождения коэффициентов 
.
Нужно представить граничное условие в виде
Следовательно, 
Далее предлагаю рассмотреть примеры решения краевых задач уравнения Гельмгольца.
Задача № 3. Решить краевую задачу для уравнения Гельмгольца в круге
(здесь 
, где 
– собственное значение однородной задачи Дирехле для уравнения 
).
Решение: Используя метод разделения переменных (метод Фурье). Полагая, 
и подставляя предполагаемую форму решения в Уравнении Гельмгольца, получается
где – постоянная разделения.
Собственные значения и собственные функции определяются как решения данной задачи:
Выходит 
то для определения 
получается уравнение
 | (24) |
Обозначив 
, переписывается уравнение (24) в виде
Это уравнение Бесселя порядка . Его общее решение есть
где 
– функция Бесселя первого рода порядка 
– функция Бесселя второго рода порядка 
– произвольные постоянные.
Значит, решение уравнения (1) имеет вид
Поскольку 
и имеется дело с ограниченными решениями, то полагаем 
Таким образом, 
. Решение нашей задачи представляется рядом
 | (25) |
Постоянные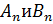 
находятся из граничного условия. Полагая в (25) 
, получаем
В частности, при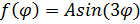 
выходит
и в этом случае решение имеет вид
В проделанной нами работе, мы акцентировали внимание на такой теме как «Уравнения эллиптического типа». В ходе нашего исследования мы сумели выполнить поставленные перед нами задачи, что повлекло за собой достижение цели работы. Изучив теоретические материалы, мы разобрались с основными уравнениями, научились выводить их и применять в решениях задач. Были обозначены проблемы и пути их решения. В качестве примера выступили три задачи, требующие решение эллиптического уравнения.
Материалом данного исследования выступали труды советских и российских деятелей, содержащие в себе подробную информацию, касающуюся нашей проблемы.
В ходе выполнения данной работы появилась возможность оценить важность заданной темы в современной науке, определить основные задачи, которые можно решать с помощью уравнений эллиптического типа.
Подводя итог, хочется отметить, что изучение данного вопроса способствовала возникновению большого интереса, что позволило с энтузиазмом продолжать с ознакомлением трудов знаменитых авторов для дальнейшего анализа и использования в работе.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1.А.Н. Тихонов, А.А. Самарский, Уравнения математической физики М., издательство «наука», 1977. – 735 с.
2. Л.Д. Ландау, Е. М. Лифшиц, Квантовая механика,
М., Изд. 4е, «Наука», 1989. – 767 с.
3. Д.А. Шапиро, Конспект лекций по методам математической физики ч.1, кафедра теоретической физики НГУ, 2004. – 123 с.
4. В. С. Владимиров, В. В. Жаринов, Уравнения математической физики. — М.: «Физматлит», 2004. – 400 с.
5. С.И. Колесникова, Методы решения основных задач уравнений математической физики, М., МФТИ, 2015. – 80 с.
Видео:Уравнения математической физики. Лекция 7: Уравнения Эллиптического типа (1). Лектор Хохлов Н.А.Скачать
Постановка задачи для уравнения эллиптического типа
Классическим примером уравнения эллиптического типа является уравнение Пуассона
или уравнение Лапласа, 
0,
которое получается из уравнения Пуассона при f(x, t) º 0.
Здесь функция u(x, t) может иметь различный физический смысл, например, описывать стационарное, независящее от времени распределение температуры, скорость потенциального (безвихревого) течения идеальной (без трения и теплопроводности) жидкости, распределение напряжённостей электрического и магнитного полей, распределение потенциала поля тяготения и т.п.
Первая краевая задача. Если на границе Г расчётной области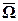 
= 
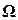
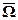
+ Г (в данном случае расчётная область 
– это сама область 
, включая её границу Г) задана искомая функция, то соответствующая первая краевая задача для уравнения Лапласа или Пуассона называется задачей Дирихле:
Вторая краевая задача. Если на границе Г расчётной области 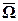задаётся нормальная производная искомой функции, то соответствующая вторая краевая задача называется задачей Неймана для уравнения Лапласа или Пуассона:
здесь n — направление внешней к границе Г нормали.
Иногда краевое условие (37) записывают в более удобном виде:
где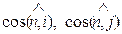 
— направляющие косинусы внешнего вектора единичной нормали к границе Г, i и j орты базисных векторов.
Третья краевая задача для уравнения Пуассона (Лапласа) имеет вид:
Замечание. Следует отметить, что в вышеперечисленных постановках задач математической физики число начальных условий равно порядку дифференциального уравнения по времени, а старший порядок производной по времени в начальных условиях на единицу меньше порядка дифференциального уравнения по времени.
Старший порядок производной по пространственной переменной в краевых условиях равен порядку дифференциального уравнения по пространственной переменной минус единица.
В одномерных задачах с одной пространственной переменной количество граничных условий точно равно порядку дифференциального уравнения по пространственной переменной.
Количество краевых условий для многомерных задач не ограничено, поскольку на разных участках границы могут быть заданы граничные условия различного рода.
Заключение (план — аннотация лекции №27).
Лекция 27 посвящена введению в приближённые методы решения дифференциальных уравнений с частными производными.
Отмечено, что при математическом анализе физических процессов, когда исследуемые свойства объекта описываются функциями не одной, а несколькими переменными, то при составлении математических моделей изучаемых явлений вместо обыкновенных дифференциальных уравнений возникают уравнения с частными производными.
В качестве примеров уравнений математической физики, наиболее востребованных на практике, рассмотрены уравнение Лапласа, уравнение Пуассона, уравнение теплопроводности (Фурье), волновое уравнение, уравнение Гельмгольца, телеграфное уравнение, уравнение переноса, уравнение акустики.
Приведена классификация уравнений с частными производными второго порядка, в основу которой положен анализ знака дискриминанта обобщённого уравнения второго порядка с частными производными.
Дана классификация методов решения уравнений с частными производными.
Обсуждаются подходы к постановке задач для уравнений математической физики. При этом корректность постановки задач связываемая с требованиями разрешимости; однозначности; непрерывной зависимости от исходных данных (иначе, устойчивости).
Рассмотрены примеры постановки задач для уравнений математической физики гиперболического, параболического и эллиптического типов.
1. И.С. Березин, Н.П. Жидков. Методы вычислений. Т. 2. – М.: Физматгиз, 1962. – 620 с.
2. В.М. Вержбицкий. Основы численных методов. – М.: Высшая школа, 2002. – 840 стр.
3. В.Ф. Формалёв, Д.Л. Ревизников. Численные методы. – М.: Физматлит, 2004. 400 с.
4. Б.П. Демидович, И.А. Марон, Э.З. Шувалова. Численные методы анализа.
– М.: Наука, 1967. – 368 с.
5. Н.В. Копчёнова, И.А. Марон. Вычислительная математика в примерах и задачах. – М.: Наука, 1972. – 368 с.
🎬 Видео
Эллиптические уравнения. ТеорияСкачать
7.1 Краевые задачи для уравнений эллиптического типа. ВступлениеСкачать
Вычислительная математика 25 Уравнения эллиптического типаСкачать
УМФ. Метод Фурье для параболического уравненияСкачать
3.1 Формула Даламбера, решение волнового уравнения на бесконечной прямойСкачать
Боголюбов А. Н. - Методы математической физики - Уравнения эллиптического типаСкачать
Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать
2. Приведение уравнений второго порядка к каноническому видуСкачать
Разностные методы решения уравнений в частных производных эллиптического типаСкачать
Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать
Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать
6.1 Смешанные краевые задачи для уравнений гиперболического и параболического типов. Метод Фурье.Скачать
6.1 Уравнение Лапласа в полярных координатах. Принцип решения и постановка задачСкачать
Метод Фурье для неоднородного уравнения теплопроводностиСкачать
11. Уравнения в полных дифференциалахСкачать
