Задачи по уравнению харди вайнберга (6 видео)

Содержание

Расчет частот аллелей в популяции и определение генетической структуры популяции
Расчет частоты аллелей в популяции лисиц
Определение частот генотипов в потомстве группы особей
Как правильно рассчитать структуру популяции по генотипам
Частота встречаемости гомозиготных растений у гречихи
Закон Харди-Вайнберга в решении генетических задач
Уравнение Харди-Вайнберга в решении генетических задач
p 2 +2pq + q 2 = 1
Примеры решений некоторых заданий с применением уравнения Харди-Вайнберга.
Задача 1. В популяции человека количество индивидуумов с карим цветом глаз составляет 51%, а с голубым – 49%. Определите процент доминантных гомозигот в данной популяции.
Задача 3. С применением формулы Харди-Вайнберга при неполном доминировании
Решение задач по теме «Закон Харди-Вайнберга»
Просмотр содержимого документа «Решение задач по теме «Закон Харди-Вайнберга»»
📺 Видео

Видео:ПОЛНЫЙ РАЗБОР ХАРДИ-ВАЙНБЕРГА // РЕШЕНИЕ ЗАДАЧ ОТ BioFamily (ЕГЭ-2024 БИОЛОГИЯ)Скачать

Расчет частот аллелей в популяции и определение генетической структуры популяции

Видео:⬆ УЧИМСЯ РЕШАТЬ РАСЧЕТНЫЕ ЗАДАЧИ НА ЗАКОН ХАРДИ-ВАЙНБЕРГАСкачать

Расчет частоты аллелей в популяции лисиц

Задача 380.
Из 14345 лисиц, изученных Ромашовым и Ильиной, 12 лисиц черные, 678 – промежуточной окраски, а 13655 лисиц – рыжие. Найдите частоты аллелей черной и рыжей окраски меха в популяции лисиц. Соответствуют ли наблюдаемые численности ожидаемым из уравнения Харди-Вайнберга?
Решение:
По условию задачи дается информация об общем количестве фенотипов особей в популяции и по каждому феноипу в отдельности. Промежуточная окраска у лисиц свидетельствует о неполном доминировании рыжей окраски, что указывает на то, что гетерозиготы и являются особями с промежуточной окраской.
Тогда
А — рыжая окраска шерсти;
а — чернафя окраска шерсти;
АА — рыжая лиса;
аа — черная лиса;
Аа — лиса с промежуточной окраской;
Nобщ. = 1445 лисиц;
р 2 (АА) = 1365 лисиц;
2pq(Aa) = 678 лисиц;
q 2 (aa) = 12 лисиц.
Найдем фенотипическую структуру популяции, получим:

p 2 + 2pq + q 2 = 1 = 100%;
р 2 (АА) = 13655/14345 = 0,9519 или 95,19%;
2pq(Aa) = 678/14345 = 0,04726 или 4,726%;
q 2 (aa) = 12/14345 = 0,000836 или 0,0836%.

1. Рассчитаем частоты аллелей черной и рыжей окраски меха в популяции лисиц
По формуле из следствия закона Харди_Вайнберга:

p – частота доминантного аллеля А, q — частота рецессивного аллеля а.

q 2( аа) = 0,000836, q = 0,02898 приблизительно 0,03;
р(А) + q(а) = 1, р(А) = 1 — q(а) = 1 — 0,03 = 0,97.

2. Рассчитаем Соответствуют ли наблюдаемые численности ожидаемым из уравнения Харди-Вайнберга:

p 2 + 2pq + q 2 = 1 = 100%;
p 2 (АА) + 2pq(Аа) + q 2 (аа) = 1 = 100%;
( 0,97) 2 + 2(0,97 • 0,03 ) + ( 0,03 ) 2 = 1 = 100%;
[0,9519 или 95,19%] + [0,04726 или 4,726%] + [0,000836 или 0,0836%] = 1 = 100%.

Значит, наблюдаемые численности лисиц по фенотипам соответствуют ожидаемым из уравнения Харди-Вайнберга.

Видео:Закон Харди — Вайнберга | НОВАЯ тема ЕГЭ по Биологии | Популяционная генетикаСкачать

Определение частот генотипов в потомстве группы особей

Задача 381.
Определите частоты доминантного и рецессивного аллелей в группе особей, состоящей из 60 гомозигот ВВ и 40 гомозигот bb; в группе, состоящей из 160 особей ВВ и 40 особей bb. Определите частоты генотипов в потомстве этих групп при условии панмиксии.
Решение:
1. Первая группа особей
N_общ. = 60 + 40 = 100
Определим частоты доминантного аллеля, получим:

р 2 (ВВ) = 60/100 = 0,6, значит р = 0,6;
q 2 (bb) = 40/100 = 0,4, значит q = 0,4.

Определите частоты генотипов в потомстве при условии панмиксии, получим:

p 2 + 2pq + q 2 = 1;
p 2 (ВВ) + 2pq(Bb) + q 2 (bb) = 1 = 100%;
(0,6) 2 + 2(0,6 • 9,4) + (0,4) 2 = [0,36 или 36%(ВВ)] + [0,48 или 48%(Bb)] + [0,16 или 16%(bb)] = 1 = 100%.

р 2 (ВВ) = 0,36 или 36%;
2pq(Bb) = 0,48 или 48%;
q 2 (bb) = 0,16 или 16%.

2. Вторая группа особей
N_общ. = 160 + 40 = 200
Определим частоты доминантного аллеля, получим:

р 2 (ВВ) = 160/200 = 0,8, значит р = 0,8;
q 2 (bb) = 40/200 = 0,2, значит q = 0,2.

Определяем частоты генотипов в потомстве при условии панмиксии, получим:

p 2 + 2pq + q 2 = 1;
p 2 (ВВ) + 2pq(Bb) + q 2 (bb) = 1 = 100%;
(0,8) 2 + 2(0,8 • 0,2) + (0,2) 2 = [0,36 или 36%(ВВ)] + [0,48 или 48%(Bb)] + [0,16 или 16%(bb)] = 1 = 100%.

р 2 (ВВ) = 0,64 или 64%;
2pq(Bb) = 0,32 или 32%;
q 2 (bb) = 0,04 или 4%.

Как правильно рассчитать структуру популяции по генотипам

Задача 382.
Доля особей, имеющих генотип (аа), в большой естественной популяции равна 0,16. Рассчитайте структуру данной популяции по генотипам.
Решение:
q 2 (aa) = 0,16 = 16%;
p 2 (AA) = ?
2pq(Aa) = ?
Зная частоту встречаемости рецессивных гомозигот (аа), рассчитаем частоту встречаемости рецессивного аллеля (а), получим:

Согласно первому следствию из закона Харди-Вайнберга рассчитаем частоту встречаемости аллеля гена (А), получим:

p + q = 1 = 100%, где
р – частота доминантного аллеля в популяции;
q — частота рецессивного аллеля в популяции.

p + q = 1; p(A) + q(a) = 1; p(A) = 1 – q(a);
p(A) = 1 – 0,4 = 0,6.

Используя второе следствие из закона Харди-Вайнберга рассчитаем структуру данной популяции по генотипам, получим:

p 2 + 2pq + q 2 = 1 = 100%, где
p 2 – частота встречаемости доминантных генотипов в популяции;
2pq — частота встречаемости гетерозигот в популяции;
q 2 — частота встречаемости рецессивных генотипов в популяции.

р 2 (АА) + 2pq(Aa) = q 2 (aa) = 1 = 100%;
(0,6) 2 + 2(0,6 • 0,4) + (0,4) 2 = 1 = 100%;
0,36 или 36%(АА) + 0,48 или 48%(Аа) + 0,16 или 16%(аа) = 1 = 100%.

Ответ:
р 2 (АА) = 36%;
q 2 (aa) = 16%;
2pq(Aa) = 48%.

Частота встречаемости гомозиготных растений у гречихи

Задача 383.
У гречихи ярко-красная окраска растений неполно доминирует над зеленой. Гетерозиготы по данным генам имеют розовую краску. В панмиктической популяции, состоящей из 840 растений, содержалось 42 красных растения. Какова частота встречаемости гомозиготных растений?
Решение:
А – ярко-красная окраска растения;
а – зеленая окраска растения;
Аа – розовая окраска растения;
N_общ. = 840 растений;
N(AA) = 42 ярко-красных растения;
р 2 = ?
q 2 = ?
1. Рассчитаем долю (частоту) встречаемости доминантных гомозигот (А) в популяции гречихи из условия задачи, получим:

р 2 (АА) = N(AA)/N_общ. = 42/840 = 0,05 или 5%.

2. Зная частоту встречаемости доминантных гомозигот (АА) в популяции рассчитаем частоту аллели гена (А), получим:

3. Согласно первому следствию из закона Харди-Вайнберга рассчитаем частоту рецессивного аллеля (а) в популяции гречихи, получим:

p + q = 1; p(A) + q(a) = 1;
q(a) = 1 – р(А) = 1 – 0,22326 = 0,7764.

4. Используя формулу Харди-Вайнберга: p 2 + 2pq + q 2 = 1 = 100%, рассчитаем частоту встречаемости рецессивных гомозигот (аа) в популяции гречихи, получим:

p 2 (AA) + 2pq(Aa) + q 2 (aa) = 1 = 100%;
q 2 (aa) = (0,7764) 2 = 0,6028 или 60,28%.

Ответ:
р 2 (АА) = 0,05 или 5%;
q 2 (aa) = 0,6028 или 60,28%.

Использование формулы Харди-Вайнберга для расчета фенотипов у кроликов

Задача 384.
У кроликов окраска волосяного покрова “шиншилла” доминирует над альбинизмом. Гетерозиготы имеют светло-серую окраску. На кролиководческой ферме среди молодняка кроликов шиншилл появились альбиносы. Из 8100 крольчат 25 оказались альбиносами. Пользуясь формулой Харди-Вайнберга, определите, сколько было получено гетерозиготных крольчат, имеющих светло-серую окраску и сколько гомозиготных крольчат, имеющих окраску “шиншилла”.
Решение:
А — окраска волосяного покрова “шиншилла”;
а — альбинизм;
Аа — гетерозигота — светло-серая окраса шерсти;
N_общ. = 8100 крольчат;
крольчата-альбиносы = 25 шт.;
p 2 (AA) = ?
2pq(Aa) = ?
q 2 (aa) = 25/8100 = 0,003086.

Зная частоту встречаемостигомозигот (аа) рассчитаем частоту аллеля (а)

q(а) = √0,003086 = 0,056.

Согласно первому следствию закона Харди-Вайнберга рассчитаем частоту встречаемости гена (А), получим:

р + q = 1, р(А) = 1 — q(а) = 1 — 0,0556 = 0,9444.

Используя формулу Харди-Вайнберга: р 2 + 2рq + q 2 = 1, рассчитаем фенотипическую структуру данной популяции кроликов, получим:

р 2 (АА) + 2рq(Аа) + q 2 (аа) = 1 = 100%;
(0,9444) 2 + (2 • 0,9444 • 0,0556) + ( 0,0556) 2 = 1 = 100%;
0,89189 или 89,2%(АА) + 0,1050 или 10,5%(Аа) + 0,00309 или 0,3%(аа) = 1 или 100%.

Рассчитаем число светло-серых крольчат, получим:

N_{(светло-серые крольчата)} = 8100 • 0,105 = 850,5 примерно 850 шт.

Рассчитаем число крольчат с окраской «шиншила», получим:

N_{(«шиншиловые» крольчата)} = 8100 • 0,892 = 7225,2 примерно 7225 шт.

Ответ:
N_{(светло-серые крольчата)} = 850 шт;
N_{(«шиншиловые» крольчата)} = 7225 шт.

Видео:Закон генетического равновесия Харди - Вайнберга. 11 класс.Скачать

Закон Харди-Вайнберга в решении генетических задач

В пределах генофонда популяции доля генотипов, содержащих разные аллели одного гена; при соблюдении некоторых условий из поколения в поколение не изменяется. Эти условия описываются основным законом популяционной генетики, сформулированным в 1908 г. английским математиком Дж. Харди и немецким врачом-генетиком Г. Вайнбергом. «В популяции из бесконечно большого числа свободно скрещивающихся особей в отсутствие мутаций, избирательной миграции организмов с различными генотипами и давления естественного отбора первоначальные частоты аллелей сохраняются из поколения в поколение».

Видео:РЕШЕНИЕ ЗАДАЧИ ЛИНИИ 27 НА УРАВНЕНИЕ ХАРДИ-ВАЙНБЕРГАСкачать

Уравнение Харди-Вайнберга в решении генетических задач

Хорошо известно, что этот закон применим лишь для идеальных популяций: достаточно высокая численность особей в популяции; популяция должна быть панмиксной, когда нет ограничения к свободному выбору полового партнера; практически должно отсутствовать мутирование изучаемого признака; отсутствует приток и отток генов и нет естественного отбора.

Закон Харди-Вайнберга формулируется следующим образом:

в идеальной популяции соотношение частот аллелей генов и генотипов из поколения в поколение является величиной постоянной и соответствует уравнению:

Видео:Закон Харди-Вайнберга - наглядное объяснение | Закон генетического равновесияСкачать

p 2 +2pq + q 2 = 1

где p 2 — доля гомозигот по одному из аллелей; p — частота этого аллеля; q 2 — доля гомозигот по альтернативному аллелю; q — частота соответствующего аллеля; 2pq — доля гетерозигот.

Что значит “соотношение частот аллелей генов” и “соотношение генотипов” – величины постоянные? Чему равны эти величины?

Пусть частота встречаемости какого-либо гена в доминантном состоянии (А) равна p, а рецессивного аллеля (а) этого же гена равна q (можно и наоборот, а можно и вообще одной буквой, выразив одно обозначение из другого) и понимая, что сумма частот доминантного и рецессивного аллелей одного гена в популяции равна 1, мы получим первое уравнение:

1) p + q = 1

Откуда берется само уравнение Харди-Вайнберга? Вы помните, что при моногибридном скрещивании гетерозиготных организмов с генотипами Аа х Аа по второму закону Менделя в потомстве мы будем наблюдать появление разных генотипов в соотношении 1АА : 2 Аа : 1аа.

Поскольку частота встречаемости доминантного аллельного гена А у нас обозначена буквой р, а рецессивного аллеля а буквой q, то сумма частот встречаемости самих генотипов организмов (АА, 2Аа и аа), имеющих эти же аллельны гены А и а, будет тоже равна 1, то:

2) p 2 AA + 2pqAa + q 2 aa = 1

В задачах по популяционной генетике, как правило, требуется:
а) найти частоты встречаемости каждого из аллельных генов по известному соотношению частот генотипов особей;

б) или наоборот, найти частоту встречаемости какого-либо из генотипов особей по известной частоте встречаемости доминантного или рецессивного аллеля изучаемого признака.

Так вот, подставляя известное значение частоты встречаемости какого-то из аллелей гена в первую формулу и найдя значение частоты встречаемости второго аллеля, мы всегда сможем по уравнению Харди-Вайнберга найти частоты встречаемости самих различных генотипов потомства.

Обычно некоторые действия (из-за их очевидности) решаются в уме. Но, чтобы было ясно то, что и так очевидно, надо хорошо понимать, что собой представляют буквенные обозначения в формуле Харди-Вайнберга.

Положения закона Харди-Вайнберга применимы и к множественным аллелям. Так, если аутосомный ген представлен тремя аллелями (А, а1 и а2), то формулы закона приобретают следующий вид:

рА + qа1 + ra2 = 1;

р 2 АА+ q 2 а1а1 + r 2 а2а2 + 2рqАа1 + 2рrАа2 + 2qrа1а2 = 1.

«В популяции из бесконечно большого числа свободно скрещивающихся особей в отсутствие мутаций, избирательной миграции организмов с различными генотипами и давления естественного отбора первоначальные частоты аллелей сохраняются из поколения в поколение».

Допустим, что в генофонде популяции, удовлетворяющей описанным условиям, некий ген представлен аллелями А₁ и А₂, обнаруживаемыми с частотой р и q . Так как других аллелей в данном генофонде не встречается, то р +q = 1. При этом q = 1—р.

Соответственно особи данной популяции образуют р гамет с аллелем А ₁ и q гамет с аллелем А₂. Если скрещивания происходят случайным образом, то доля половых клеток, соединяющихся с гаметами А ₁ , равна р, а доля половых клеток, соединяющихся с гаметами A ₂, — q. Возникающее в результате описанного цикла размножения поколение F ₁ образовано генотипами A _l A ₁, A ₁ A ₂, A ₂ A ₂, количество которых соотносится как (р + q) (р + q) = р 2 + 2 pq + q 2 (рис. 10.2). По достижении половой зрелости особи AlAi и АгА2 образуют по одному типу гамет — A ₁ или A ₂ — с частотой, пропорциональной числу организмов указанных генотипов (р и q). Особи A ₁ A ₂ образуют оба типа гамет с равной частотой 2 pq /2.

Рис. Закономерное распределение генотипов в ряду поколений в зависимости от частоты образования гамет разных типов (закон Харди—Вайнберга)

Таким образом, доля гамет A ₁ в поколении F ₁ составит р 2 + 2pq/2 = р 2 + р(1—р) = p, а доля гамет А₂ будет равна q 2 + 2pq/2 = q 2 + + q ( l — q ) = q .

Так как частоты гамет с разными аллелями в поколении fi в сравнении с родительским поколением не изменены, поколение F 2 будет представлено организмами с генотипами A _l A ₁ , A ₁ A ₂ и А₂А₂ в том же соотношении р 2 + 2pq + q 2 . Благодаря этому очередной цикл размножения произойдет при наличии р гамет A ₁ и q гамет А₂. Аналогичные расчеты можно провести для локусов с любым числом аллелей. В основе сохранения частот аллелей лежат статистические закономерности случайных событий в больших выборках.

Уравнение Харди—Вайнберга в том виде, в котором оно рассмотрено выше, справедливо для аутосомных генов. Для генов, сцепленных с полом, равновесные частоты генотипов A _l A ₁ , A ₁ A ₂ и А₂А₂ совпадают с таковыми для аутосомных генов: р 2 + 2pq + q 2 . Для самцов (в случае гетерогаметного пола) в силу их гемизиготности возможны лишь два генотипа A ₁ — или А₂ —, которые воспроизводятся с частотой, равной частоте соответствующих аллелей у самок в предшествующем поколении: р и q. Из этого следует, что фенотипы, определяемые рецессивными аллелями сцепленных с хромосомой Х генов, у самцов встречаются чаще, чем у самок.

Так, при частоте аллеля гемофилии, равной 0,0001, это заболевание у мужчин данной популяции наблюдается в 10 000 раз чаще, чем у женщин (1 на 10 тыс. у первых и 1 на 100 млн. у вторых).

Еще одно следствие общего порядка заключается в том, что в случае неравенства частоты аллеля у самцов и самок разность между частотами в следующем поколении уменьшается вдвое, причем меняется знак этой разницы. Обычно требуется несколько поколений для того, чтобы возникло равновесное состояние частот у обоих полов. Указанное состояние для аутосомных генов достигается за одно поколение.

Закон Харди — Вайнберга описывает условия генетической стабильности популяции. Популяцию, генофонд которой не изменяется в ряду поколений, называют менделевской. Генетическая стабильность менделевских популяций ставит их вне процесса эволюции, так как в таких условиях приостанавливается действие естественного отбора. Выделение менделевских популяций имеет чисто теоретическое значение. В природе эти популяции не встречаются. В законе Харди — Вайнберга перечислены условия, закономерно изменяющие генофонды популяций. К указанному результату приводят, например, факторы, ограничивающие свободное скрещивание (панмиксию), такие, как конечная численность организмов в популяции, изоляционные барьеры, препятствующие случайному подбору брачных пар. Генетическая инертность преодолевается также благодаря мутациям, притоку в популяцию или оттоку из нее особей с определенными генотипами, отбору.

Видео:Уравнение Харди-ВайнбергаСкачать

Примеры решений некоторых заданий с применением уравнения Харди-Вайнберга.

Задача 1. В популяции человека количество индивидуумов с карим цветом глаз составляет 51%, а с голубым – 49%. Определите процент доминантных гомозигот в данной популяции.

Сложность решения подобных заданий в их кажущейся простоте. Раз так мало данных, то и решение должно быть как-будто очень короткое. Оказывается не очень.

По условию подобного рода заданий нам, как правило, дается информация об общем количестве фенотипов особей в популяции. Поскольку фенотипы особей в популяции с доминантными признаками могут быть представлены как гомозиготными по генотипу особями АА, так и гетерозиготными Аа, то для определения частот встречаемости каких-то конкретных генотипов особей в этой популяции, необходимо предварительно вычислить частоты встречаемости аллелей гена А и а по отдельности.

Как мы должны рассуждать при решении этой задачи?

Поскольку известно, что карий цвет глаз доминирует над голубым, обозначим аллель, отвечающий за проявление признака кареглазости А, а аллельный ему ген, ответственный за проявление голубых глаз, соответственно, а. Тогда кареглазыми в исследуемой популяции будут люди как с генотипом АА (доминантные гомозиготы, долю которых и надо найти по условию задачи), так и — Аа гетерозиготы), а голубоглазыми – только аа (рецессивные гомозиготы).

По условию задачи нам известно, что количество людей с генотипами АА и Аа составляет 51%, а количество людей с генотипом аа — 49%. Как, исходя из этих статистических данных (большая выборка должна быть, репрезентативная), можно вычислить процент кареглазых людей только с генотипом АА?

Для этого вычислим частоты встречаемости каждого из аллельных генов А и а в данной популяции людей. Закон Харди-Вайнберга, применяемый для больших свободно скрещивающихся популяций, как раз и позволит нам сделать это.

Обозначив частоту встречаемости аллеля А в данной популяции буквой q, имеем частоту встречаемости аллельного ему гена а = 1 – q. (Можно было бы обозначить частоту встречаемости аллельного гена а отдельной буквой, как в тексте выше – это кому как удобнее). Тогда сама формула Харди-Вайнберга для расчета частот генотипов при моногибридном скрещивании при полном доминировании одного аллельного гена над другим будет выглядеть вот так:

q 2 AA+ 2q(1 – q)Aa + (1 – q) 2 aa = 1.

Ну, а теперь уже все просто, вы наверняка все догадались, что в этом уравнении нам известно, а что следует найти?

(1 – q) 2 = 0,49 – это частота встречаемости людей с голубыми глазами.

Находим значение q: 1 – q = корень квадратный из 0,49 = 0,7; q = 1 – 0,7 = 0,3, тогда q2 = 0,09.
Это значит, что частота кареглазых гомозиготных особей АА в данной популяции будет составлять 0,09 или доля их будет равна 9%.

Задача 2. У клевера лугового поздняя спелость доминирует над скороспелостью и наследуется моногено. При апробации установлено, что 4% растений относятся к раннеспелому типу клевера, какую часть от позднеспелых растений составляют гетерозиготы?

В данном контексте апробация означает оценку чистоты сорта. А что, разве сортом не является чистая линия как сорта гороха у Менделя, например. Теоретически “да”, но на практике (поля то большие – это не опытные делянки гениального Менделя) в каждом производственном сорте могут находиться в каком-то количестве и “мусорные” аллели генов.

В данном случае с позднеспелым сортом клевера, если бы сорт был чистым, присутствовали бы только растения с генотипом АА. Но сорт оказался на момент проверки (апробации) не очень чистым, так как 4% особей составляли раннеспелые растения с генотипом аа. Значит в этот сорт “затесались” аллели а.

Так вот, раз они “затесались”, то в данном сорте должны присутствовать и особи, хотя по фенотипу и позднеспелые, но гетерозиготные с генотипом Аа — их количество нам и надо определить?

По условию задачи 4% особей с генотипом аа составят 0,04 часть от всего сорта. Фактически это q 2 , значит частота встречаемости рецессивного аллеля а равна q = 0,2. Тогда частота встречаемости доминантного аллеля А равна p = 1 – 0,2 = 0,8.

Отсюда количество позднеспелых гомозигот p2 = 0,64 или 64%. Тогда количество гетерозигот Аа будет составлять 100% – 4% – 64% = 32%. Поскольку всего позднеспелых растений 96%, то доля гетерозигот среди них составит: 32 х 100 : 96 = 33,3%.

Задача 3. С применением формулы Харди-Вайнберга при неполном доминировании

При обследовании популяции каракульских овец было выявлено 729 длинноухих особей (АА), 111 короткоухих (Аа) и 4 безухих (аа). Вычислите наблюдаемые частоты фенотипов, частоты аллелей, ожидаемые частоты генотипов по формуле Харди-Вайнберга.

Это задача по неполному доминированию, поэтому, распределение частот генотипов и фенотипов совпадают и их можно было бы определить, исходя из имеющихся данных. Для этого надо просто найти сумму всех особей популяции (она равна 844), найти долю длинноухих, короткоухих и безухих сначала в процентах (86.37, 13.15 и 0.47, соответственно) и в долях частот (0.8637, 0.1315 и 0.00474).

Но в задании сказано применить для расчетов генотипов и фенотипов формулу Харди-Вайнберга и, к тому же, рассчитать частоты аллелей генов А и а. Так вот для расчета самих частот аллелей генов без формулы Харди-Вайнберга не обойтись.

Обратите внимание, что в этой задаче, в отличие от предыдущей, для обозначения частот аллельных генов, мы будем пользоваться приемом обозначений не как в первой задаче, а как разбиралось выше в тексте. Понятно, что результат от этого не изменится, но вы будете в праве в будущем использовать любой из этих способов обозначений, какой вам кажется более удобным для понимания и проведения самих расчетов.

Обозначим частоту встречаемости аллеля А во всех гаметах популяции овец буквой р, а частоту встречаемости аллеля а — буквой q. Помним, что сумма частот аллельных генов p + q = 1.

Так как по формуле Харди-Вайнберга p 2 AA + 2pqAa + q 2 aa = 1 имеем, что частота встречаемости безухих q2 равна 0.00474, то извлекая квадратный корень из числа 0.00474 мы находим частоту встречаемости рецессивного аллеля а. Она равна 0.06884.

Отсюда мы можем найти частоту встречаемости и доминантного аллеля А. Она равна 1 – 0.06884 = 0.93116.

Теперь по формуле можем вычислить снова частоты встречаемости длинноухих (АА), безухих (аа) и короткоухих (Аа) особей. Длинноухих с генотипом АА будет р 2 = 0.931162 = 0.86706, безухих с генотипом аа будет q 2 = 0.00474 и короткоухих с генотипом Аа будет 2pq = 0,12820. (Вновь полученные числа, рассчитанные по формуле, почти совпадают с вычисленными изначально, что говорит о справедливости закона Харди-Вайнберга).

Задача 4. Почему доля альбиносов в популяциях так мала

В выборке, состоящей из 84 000 растений ржи, 210 растений оказались альбиносами, т.к. у них рецессивные гены находятся в гомозиготном состоянии. Определите частоты аллелей А и а, а также частоту гетерозиготных растений.

Обозначим частоту встречаемости доминантного аллельного гена А буквой p, а рецессивного а – буквой q. Тогда, что нам может дать формула Харди-Вайнберга p 2 AA + 2pqAa + q 2 aa = 1 для применения её к этой задаче?

Поскольку общая численность всех особей данной популяции ржи нам известна 84000 растений, а в частях это и есть 1, то доля гомозиготных альбиносных особей с генотипом аа равная q2, которых всего 210 штук, составит q2 = 210 : 84000 = 0,0025, тогда q = 0,05; p = 1 – q = 0,95 и тогда 2pq = 0,095.

Ответ: частота аллеля а – 0,05; частота аллеля А – 0,95; частота гетерозиготных растений с генотипом Аа составит 0,095.

Задача 5. Выращивали кроликов шиншилл, а получили брак в виде альбиносиков

У кроликов окраска волосяного покрова “шиншилла” (ген Cch) доминирует над альбинизмом (ген Ca). Гетерозиготы CchCa имеют светло-серую окраску. На кролиководческой ферме среди молодняка кроликов шиншилл появились альбиносы. Из 5400 крольчат 17 оказались альбиносами. Пользуясь формулой Харди-Вайнберга, определите, сколько было получено гомозиготных крольчат с окраской шиншилла.

А как Вы думаете, полученная выборка в популяции кроликов в количестве 5400 экземпляров, может позволить нам использовать формулу Харди-Вайнберга? Да выборка значительная, популяция изолированная (кролиководческая ферма) и действительно можно применить в расчетах формулу Харди-Вайнберга.Чтобы правильно её использовать, надо четко представлять что нам дано, а что требуется найти.

Лишь для удобства оформления, обозначим генотип шиншилл АА (количество их нам и надо будет определить), генотип альбиносиков аа, тогда генотип гетерозиготных серячков будет обозначаться Аа.

Если “сложить” всех кроликов с разными генотипами в изучаемой популяции: АА + Аа + аа, то это и будет в сумме 5400 штук особей.
Да еще нам известно, что кроликов с генотипом аа было 17 штук. Как же нам теперь, не зная сколько было гетерозиготных серых кроликов с генотипом Аа, определить сколько в этой популяции шиншилл с генотипом АА?

Как мы можем видеть эта задача является почти “копией” первой, только там нам даны были результаты подсчетов в популяции людей кареглазых и голубоглазых индивидов в %, а здесь фактически нам известна сама численность альбиносов кроликов 17 штук и всех гомозиготных шиншилл и гетерозиготных серячков в сумме: 5400 – 17 = 5383 штук.

Примем 5400 штук всех кроликов за 100%, тогда 5383 кролика (сумма генотипов АА и Аа) составит 99,685% или в частях это будет 0,99685.

q 2 + 2q(1 – q) = 0,99685 – это частота встречаемости всех шиншилл и гомозиготных (АА), и гетерозиготных (Аа).

Тогда из уравнения Харди-Вайнберга: q2 AA+ 2q(1 – q)Aa + (1 – q)2aa = 1 , находим

(1 – q) 2 = 1 – 0,99685 = 0,00315 — это частота встречаемости альбиносных кроликов с генотипом аа. Находим чему равна величина 1 – q. Это корень квадратный из 0,00315 = 0,056. А q тогда равняется 0,944.

q 2 равняется 0,891, а это и есть доля гомозиготных шиншил с генотипом АА. Так как эта величина в % составит 89,1% от 5400 особей, то количество гомозиготных шиншилл будет 4811 шт.

Задача 6. Определение частоты встречаемости гетерозиготных особей по известной частоте встречаемости рецессивных гомозигот

Одна из форм глюкозурии наследуется как аутосомно-рецессивный признак и встречается с частотой 7:1000000. Определить частоту встречаемости гетерозигот в популяции.

Обозначим аллельный ген, отвечающий за проявление глюкозурии а, так как сказано, что это заболевание наследуется как рецессивный признак. Тогда аллельный ему доминантный ген, отвечающий за отсутствие болезни обозначим А.

Здоровые особи в популяции людей имеют генотипы АА и Аа; больные особи имеют генотип только аа.

Обозначим частоту встречаемости рецессивного аллеля а буквой q, а доминантного аллеля А – буквой р.

Поскольку нам известно, что частота встречаемости больных людей с генотипом аа (а это значит q 2 ) равна 0,000007, то q = 0,00264575

Так как p + q = 1, то р = 1 — q = 0,9973543, и p2 = 0,9947155

Теперь подставив значения р и q в формулу:

p2AA + 2pqAa + q2aa = 1,

найдем частоту встречаемости гетерозиготных особей 2pq в популяции людей:

2pq = 1 — p 2 — q 2 = 1 – 0,9947155 – 0,000007 = 0,0052775.

Задача 7. Как и предыдущая задача, но про альбинизм

Альбинизм общий (молочно-белая окраска кожи, отсутствие меланина в коже, волосяных луковицах и эпителии сетчатки) наследуется как рецессивный аутосомный признак. Заболевание встречается с частотой 1 : 20 000 (К. Штерн, 1965). Определите процент гетерозиготных носителей гена.

Так как этот признак рецессивный, то больные организмы будут иметь генотип аа — это их частота равна 1 : 20 000 или 0,00005.

Частота аллеля а составит корень квадратный из этого числа, то есть 0,0071. Частота аллеля А составит 1 — 0,0071 = 0,9929, а частота здоровых гомозигот АА будет 0,9859.

Частота всех гетерозигот 2Аа = 1 — (АА + аа) = 0,014 или 1,4%.

Задача 8. Кажется, как все просто, когда знаешь как решать

Популяция европейцев по системе групп крови резус содержит 85% резус положительных индивидуумов. Определите насыщенность популяции рецессивным аллелем.

Нам известно, что аллельный ген, отвечающий за проявление резус положительной крови является доминантным R (обозначим частоту его встречаемости буквой p), а резус отрицательный – рецессивным r (обозначим частоту встречаемости его буквой q).

Поскольку в задаче сказано, что на долю p 2 RR + 2pqRr приходится 85% людей, значит на долю резус-отрицательных фенотипов q 2 rr будет приходиться 15% или частота встречаемости их составит 0,15 от всех людей европейской популяции.

Тогда частота встречаемости аллеля r или ”насыщенность популяции рецессивным аллелем” (обозначенная буквой q) составит корень квадратный из 0,15 = 0,39 или 39%.

Задача 9. Главное знать что такое пенетрантность

Врожденный вывих бедра наследуется доминантно. Средняя пенетрантность составляет 25%. Заболевание встречаются с частотой 6:10000. Определите число гомозиготных особей в популяции по рецессивному признаку.

Пенетрантность — это количественный показатель фенотипической изменчивости проявления гена.

Пенетрантность измеряется в процентном отношении числа особей, у которых данный ген проявился в фенотипе к общему числу особей, в генотипе которых этот ген присутствует в необходимом для его проявления состоянии (гомозиготном — в случае рецессивных генов или гетерозиготном — в случае доминантных генов). Проявление гена у 100% особей с соответствующим генотипом называется полной пенетрантностью, а в остальных случаях — неполной пенетрантностью.

За изучаемый признак отвечает доминантный аллель, обозначим его А. Значит организмы, имеющие данное заболевание имеют генотипы АА и Аа.

Известно, что фенотипически вывих бедра выявляется у 6 организмов из всей популяции (10000 обследованных), но это лишь одна четвертая часть из всех людей, реально имеющих генотипы АА и Аа (так как сказано, что пенетрантность составляет 25%).

Значит на самом деле людей с генотипами АА и Аа в 4 раза больше, то есть 24 из 10000 или 0,0024 часть. Тогда людей с генотипом аа будет 1 – 0,0024 = 0,9976 часть или 9976 человек из 10000.

Задача 10. Если болеют только мужчины

Подагра встречается у 2% людей и обусловлена аутосомным доминантным геном. У женщин ген подагры не проявляется, у мужчин пенетрантность его равна 20% (В.П. Эфроимсон, 1968). Определите генетическую структуру популяции по анализируемому признаку, исходя из этих данных.

Так как подагра выявляется у 2% мужчин, то есть у 2 человек из 100 с пенетрантностью 20%, то реально носителями генов подагры является в 5 раз больше мужчин, то есть 10 человек из 100.

Но, так как мужчины составляют лишь пол популяции, то всего людей с генотипами АА + 2Аа в популяции будет 5 человек из 100, а, значит, 95 из 100 будут с генотипом аа.

Если частота встречаемости организмов с генотипами аа составляет 0,95, то частота встречаемости рецессивного аллеля а в этой популяции равна корню квадратному из числа 0,95 = 0,975. Тогда частота встречаемости доминантного аллеля ”А” в этой популяции равна 1 – 0,975 = 0,005.

Задача 11. Как мало людей устойчивых к ВИЧ инфекции

Устойчивость к ВИЧ-инфекции связана с наличием в генотипе некоторых рецессивных генов, например, ССR и SRF. Частота рецессивного аллеля ССR-5 в русской популяции составляет 0,25%, а аллеля SRF – 0,05%. В казахской популяции частота этих аллелей соответственно – 0,12% и 0,1%. Рассчитайте частоты организмов, имеющих повышенную устойчивость к ВИЧ-инфекции, в каждой из популяций.

Понятно, что повышенной устойчивостью к ВИЧ-инфекции будут обладать лишь гомозиготные организмы с генотипами аа. Организмы же с генотипами АА (гомозиготы) или Аа (гетерозиготы) не устойчивы к ВИЧ инфекции.

В русской популяции устойчивых организмов по аллельному гену ССR будет О,25% в квадрате = 0,0625%, а по аллельному гену SRF 0,05% в квадрате = 0,0025%.

В казахской популяции устойчивых организмов по аллельному гену ССR будет О,12% в квадрате = 0,0144%, а по аллельному гену SRF 0,1% в квадрате = 0,01%.

Видео:Решаем задачи на Харди-Вайнберга в ЕГЭ по биологииСкачать

Решение задач по теме «Закон Харди-Вайнберга»

Для того чтобы описывать генетические свойства популяции, вводится понятие генофонда: совокупности генов, встречающихся в данной популяции. Помимо генофонда важны также частота встречаемости гена или частота встречаемости аллеля.

Знание того, как реализуются законы наследования на уровне популяций, принципиально важно для понимания причин индивидуальной изменчивости. Все закономерности, выявляемые в ходе психогенетических исследований, относятся к конкретным популяциям. В других популяциях, с иным генофондом и другими частотами генов, могут получаться отличающиеся результаты.

Закон Харди-Вайнберга— основа математических построений генетики популяций и современной эволюционной теории.

Данная разработка содержит теоретический материал по теме и примеры решения задач на применение данного закона.

Просмотр содержимого документа
«Решение задач по теме «Закон Харди-Вайнберга»»

Популяционная генетика занимается генетической структурой популяций.

Понятие «популяция» относится к совокупности свободно скрещивающихся особей одного вида, длительно существующей на определенной территории (части ареала) и относительно обособленной от других совокупностей того же вида.

Важнейший признак популяции — это относительно свободное скрещивание. Если возникают какие-либо изоляционные барьеры, препятствующие свободному скрещиванию, то возникают новые популяции.

У человека, например, помимо территориальной изоляции, достаточно изолированные популяции могут возникать на основе социальных, этнических или религиозных барьеров. Поскольку между популяциями не происходит свободного обмена генами, то они могут существенно различаться по генетическим характеристикам. Для того чтобы описывать генетические свойства популяции, вводится понятие генофонда: совокупности генов, встречающихся в данной популяции. Помимо генофонда важны также частота встречаемости гена или частота встречаемости аллеля.

Закон Харди-Вайнберга— основа математических построений генетики популяций и современной эволюционной теории. Сформулирован независимо друг от друга математиком Г. Харди (Англия) и врачом В. Вайнбергом (Германия) в 1908 г. Этот закон утверждает, что частоты аллелей и генотипов в данной популяции будут оставаться постоянными из поколения в поколение при выполнении следующих условий:

1) численность особей популяции достаточно велика (в идеале — бесконечно велика),

2) спаривание происходит случайным образом (т. е. осуществляется панмиксия),

3) мутационный процесс отсутствует,

4) отсутствует обмен генами с другими популяциями,

5) естественный отбор отсутствует, т. е. особи с разными генотипами одинаково плодовиты и жизнеспособны.

Иногда этот закон формулируют иначе: в идеальной популяции частоты аллелей и генотипов постоянны. (Поскольку описанные выше условия выполнения данного закона и есть свойства идеальной популяции.)

Математическая модель закона отвечает формуле:

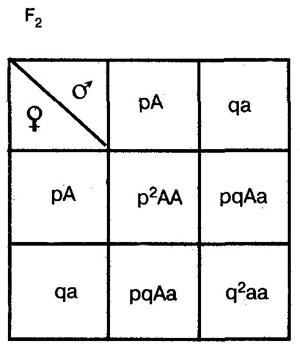
Она выводится на основе следующих рассуждений. В качестве примера возьмем простейший случай — распределение двух аллелей одного гена. Пусть два организма являются основателями новой популяции. Один из них является доминантной гомозиготой (АА), а другой — рецессивной гомозиготой (аа). Естественно, что все их потомство в F₁ будет единообразным и будет иметь генотип (Аа). Далее особи F₁ будут скрещиваться между собой. Обозначим частоту встречаемости доминантного аллеля (А) буквой p, а рецессивного аллеля (а) — буквой q. Поскольку ген представлен всего двумя аллелями, то сумма их частот равна единице, т. е. р + q = 1. Рассмотрим все яйцеклетки в данной популяции. Доля яйцеклеток, несущих доминантный аллель (А), будет соответствовать частоте этого аллеля в популяции и, следовательно, будет составлять р. Доля яйцеклеток, несущих рецессивный аллель (а), будет соответствовать его частоте и составлять q. Проведя аналогичные рассуждения для всех сперматозоидов популяции, придем к заключению о том, что доля сперматозоидов, несущих аллель (А), будет составлять р, а несущих рецессивный аллель (а) — q. Теперь составим решетку Пеннета, при этом при написании типов гамет будем учитывать не только геномы этих гамет, но и частоты несомых ими аллелей. На пересечении строк и столбцов решетки мы получим генотипы потомков с коэффициентами, соответствующими частотам встречаемости этих генотипов.