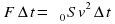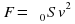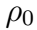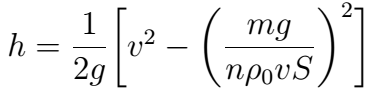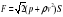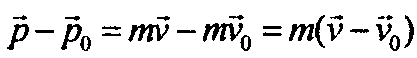Задачи на уравнение неразрывности бернулли 10 класс (6 видео)

Содержание

Самостоятельная работа по физике Движение жидкости. Уравнение Бернулли 10 класс
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Конспект по физике на тему «Уравнение Бернулли» (10 класс)
Задачи по гидродинамике (ЕГ)
Просмотр содержимого документа «Задачи по гидродинамике (ЕГ)»
📽️ Видео

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Самостоятельная работа по физике Движение жидкости. Уравнение Бернулли 10 класс

Самостоятельная работа по физике Движение жидкости. Уравнение Бернулли 10 класс с ответами. Самостоятельная работа включает 5 вариантов, в каждом по 2 задания.

Видео:Уравнение Бернулли. Практическая часть. 10 класс.Скачать

Вариант 1

1. По горизонтальной трубе переменного сечения течёт жидкость. Скорость течения в широкой части трубы 2 м/с. Определите скорость течения в узкой части трубы, если площади поперечного сечения этих частей трубы различаются в 1,5 раза.

2. В цилиндрическом сосуде уровень воды составляет 20 см. С какой скоростью начнёт вытекать вода, если открыть кран, установленный у основания этого сосуда?

Видео:Физика. 10 класс. Уравнение неразрывности. Уравнение Бернулли. Подъёмная сила /29.10.2020/Скачать

Вариант 2

1. По горизонтальной трубе переменного сечения течёт вода. Скорость течения в широкой части трубы 5 м/с, в узкой — 20 м/с. Во сколько раз различаются диаметры сечений этой трубы?

2. Скорость истечения воды из бассейна по трубе, расположенной в основании бассейна, составляет 10 м/с. Определите глубину бассейна.

Видео:Урок 134. Применения уравнения Бернулли (ч.1)Скачать

Вариант 3

1. На вертикальную стену, действуя перпендикулярно, ветер оказывает давление 100 Па. Определите скорость ветра, если плотность воздуха равна 1,29 кг/м 3 .

2. Подводная лодка находится на глубине 100 м. С какой скоростью будет поступать вода в лодку, если открыть люк? Давление воздуха в лодке считайте равным атмосферному.

Видео:Гидродинамика. Уравнение Бернулли. Физика 10 классСкачать

Вариант 4

1. Из брандспойта вертикально вверх бьёт струя воды с расходом 1 кг за 1 с. Площадь поперечного сечения у основания струи равна 1,5 см 2 . Определите площадь поперечного сечения струи на высоте 2 м.

2. В горизонтальной трубе переменного сечения течёт вода. Площадь поперечного сечения широкой части трубы равна 20 см 2 , узкой — 10 см 2 . Разность уровней воды в вертикальных трубках одинакового сечения равна 20 см (см. рисунок).

Определите объём воды, протекающей через поперечное сечение за 1 с.

Видео:Теория вероятностей #8: формула Бернулли и примеры ее использования при решении задачСкачать

Вариант 5

1. Для смазки инструмента используется шприц с площадью поршня 1 см 2 . С какой скоростью вытекает масло (ρ_м = 800 кг/м 3 ) из отверстия площадью 0,6 см 2 , если на поршень действует сила 4 Н?

2. Определите высоту, на которую поднимется вода в вертикальной трубке, впаянной в узкую часть (диаметром 3 см) горизонтальной
трубы (см. рисунок), если в широкой части этой же трубы (диаметром в 3 раза большим) скорость протекания воздуха составляет 0,25 м/с.

Ответы на самостоятельную работа по физике Движение жидкости. Уравнение Бернулли 10 класс
Вариант 1
1. 3 м/с
2. 2 м/с
Вариант 2
1. В 2 раза
2. 5 м
Вариант 3
1. ≈ 6,23 м/с
2. ≈ 44,72 м/с
Вариант 4
1. 4,8 см 2
2. ≈ 2,3 л
Вариант 5
1. 12,5 м/с
2. 0,255 м

Видео:Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Конспект по физике на тему «Уравнение Бернулли» (10 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Зависимость давления жидкости от скорости ее течения. Движение тел в жидкостях и газах. Уравнение Бернулли. Использование и учет его в технике и жизни .

Один из способов наблюдения течения жидкости состоит в том, что к жидкости подмешивают алюминиевый порошок и следят при сильном освещении за движением алюминиевых блесток. При этом траектории движения этих частиц будут совпадать с линиями тока.

Линии тока – линии, проведенные так, что касательные к ним совпадают по направлению со скоростями частиц жидкости в соответствующих точках пространства.

Свойства линий тока:

1) Цепочки, которые образует алюминиевый порошок, показывают форму линий тока.

2) Через любую точку жидкости можно провести линию тока.

3) Направление линий тока определяется направлением скорости частиц жидкости в данной точке.

4) Густота линий тока характеризует величину скорости в разных точках пространства текущей жидкости: там, где линии тока расположены гуще, скорость больше; там, где линии тока расположены реже, скорость меньше.

Трубка тока – объем жидкости, ограниченный линиями тока.

Скорости элементов жидкости в каждой точке поверхности трубки направлены по касательной к этой поверхности, поэтому частицы при своем движении не пересекают стенок трубки тока.

Различают два вида движения жидкостей:

движение жидкости, при котором отдельные ее слои скользят друг относительно друга, не перемешиваясь.

Движение жидкости, сопровождающееся перемешиванием ее различных слоев с образованием завихрений.

Примеры: течение воды в спокойных реках,

Примеры: поток быстрых рек, океанские течения.

Для описания движения жидкости обычно пользуются следующим методом: фиксируют скорости различных элементов жидкости в одних и тех же точках пространства. Кинематически описать движение реальных жидкостей достаточно сложно. Примем некоторые допущения для упрощения задачи:

1) Ограничимся рассмотрением ламинарного течения.

2) При описании движения жидкости будем рассматривать идеальные жидкости:

Идеальная жидкость – жидкость, вязкостью и сжимаемостью которой можно пренебречь.

Когда мы говорим, что жидкость несжимаема, то имеем в виду, что она не может быть сжата настолько, чтобы заметно изменился ее объем, но очень малое сжатие, вызывающее появление сил упругости, неизбежно происходит.

Вязкость – свойство жидкости оказывать сопротивление относительному перемещению своих частей. Вязкость обусловлена наличием сил внутреннего трения в жидкости.

3) Будем считать, что движение жидкости стационарное:

Скорости элементов жидкости в различных точках пространства, вообще говоря, различны. Если во всех точках пространства скорости элементов жидкости не меняются со временем, то движение жидкости называется стационарным (установившимся).

При стационарном течении любая частица жидкости проходит данную точку с одним и тем же значением скорости. В другой какой-либо точке скорость частицы будет иной, но также постоянной во времени для всех частиц.

Картина линий тока при стационарном течении остается неизменной. Линии тока в этом случае совпадают с траекториями частиц.

Рассмотрим ламинарное течение идеальной жидкости по трубе переменного сечения. Разобьем жидкость на отдельные трубки тока, настолько тонкие, что в каждом сечении скорости элементов жидкости можно считать одинаковыми.

Рассмотрим два сечения S ₁ и S ₂ . Обозначим через и соответствующие скорости течения жидкости.

За малое время Δ t через первое сечение проходит жидкость, масса которой равна: , а через второе — .

Для несжимаемой жидкости и , так как жидкость не пересекает стенок трубки и не может в ней накапливаться. Следовательно:

–уравнение неразрывности несжимаемой жидкости:

модули скоростей несжимаемой жидкости в двух сечениях трубки тока обратно пропорциональны площадям сечений.

Это уравнение справедливо как для стационарного, так и для нестационарного течения.

Давление внутри неподвижной жидкости передается в любую точку этой жидкости без изменений (закон Паскаля). Выясним распределение давления в движущейся жидкости.

Рассмотрим следующий опыт. Возьмем трубку переменного сечения с небольшими отверстиями в стенке, в которые вставлены открытые сверху измерительные трубки. При стационарном течении жидкость в каждой измерительной трубке поднимается до определенной высоты, отсчитываемой от горизонтального уровня. По высоте столба жидкости можно судить о ее давлении на стенки горизонтальной трубки. Опыт показывает, что в широких местах трубки давление больше, чем в узких. Но, согласно уравнению неразрывности несжимаемой жидкости, чем больше сечение трубки, тем меньше скорость течения жидкости. Следовательно, можно сделать вывод:

Закон Бернулли: при стационарном течении жидкости давление больше в тех местах, где меньше скорость течения, и наоборот, меньше в тех местах, где больше скорость течения.

Объяснить результат эксперимента можно следующим образом. Так как при переходе жидкости с участка трубы с большей площадью сечения, на участок с меньшей площадью сечения скорость течения увеличивается, то жидкость движется с ускорением, направленным по течению. При переходе жидкости из узкой части в широкую, скорость течения уменьшается, жидкость движется с ускорением, направленным против течения. Согласно II закону Ньютона ускорение вызывается силой и совпадает с ней по направлению. Такой силой может быть лишь равнодействующая сил давления окружающей жидкости на поверхность выделенного объема. Сила давления представляет собой силу упругости сжатой жидкости. Таким образом, в широком участке трубы давление жидкости должно быть больше, чем в узком участке трубы.

Установим зависимость давления идеальной жидкости от скорости ее стационарного течения математически. Пусть труба переменного сечения расположена наклонно к горизонту. Система труба-жидкость-Земля является замкнутой и потенциальной. Воспользуемся теоремой об изменении кинетической энергии.

Согласно теореме об изменении потенциальной энергии:

По определению работы:

(где

— уравнение Бернулли.

где — плотность кинетической энергии или динамическое давление (обусловленное );

— плотность потенциальной энергии или гидростатическое давление (обусловленное гравитационного взаимодействия);

— статическое давление (обусловленное упругого взаимодействия)

Согласно уравнению Бернулли: сумма давления и плотностей кинетической и потенциальной энергий при стационарном течении идеальной жидкости остается постоянной для любого сечения потока.

Если труба горизонтальна, то и уравнение примет вид:

Это уравнение показывает, что с увеличением скорости течения давление в жидкости, текущей по горизонтальной трубе, уменьшается .

Применение уравнения Бернулли:

1) Измерение давления и скорости.

Для измерения давления в текущей жидкости используют манометрические трубки, имеющие Г-образную форму с отверстиями. Если располагать трубку, чтобы отверстие было направлено навстречу потоку, скорость жидкости перед отверстием равно нулю; линии тока перед манометром расходятся, не попадая в область перед отверстием. Подставляя в уравнение Бернулли , имеем:

Давление можно измерить с помощью манометрической трубки, помещенной в поток жидкости отверстием вверх (плоскость отверстия расположена параллельно линиям тока). Течение жидкости вдоль боков трубки остается практически таким же как и без трубки, следовательно, показания манометра будут совпадать с показаниями манометра, который движется вместе с жидкостью.

Манометр, обращенный отверстием к потоку, измерит большее давление , чем манометр с отверстием, параллельным линиям тока . Избыток давления получается потому, что частицы жидкости тормозятся перед манометром, вследствие этого давление повышается.

Измерив давление и , можно определить скорость потока:

Эта формула может быть использована для измерения скорости подводной лодки или самолета.

2) Определение скорости истечения жидкостей из отверстия в сосуде.

С помощью уравнения Бернулли можно найти скорость истечения идеальной жидкости из отверстия расположенного в сосуде на глубине h относительно поверхности жидкости. Если сосуд широкий, а отверстие мало, то скорости жидкости в сосуде малы. Ко всему потоку жидкости в целом можно применить уравнение Бернулли. В верхнем сечении у поверхности давление равно атмосферному, а скорость . В нижнем сечении трубки – в отверстии давление также равно атмосферному. Если скорость в отверстии обозначить через , то из уравнения Бернулли для этих двух сечений получим:

Истечение идеальной жидкости происходит с той же скоростью, какую имело бы тело при свободном падении с высоты h .

Применение уравнения Бернулли в технике:

1) Водоструйный насос.

Струя воды подается в трубку А, имеющую на одном конце сужение. По сужению вода течет с большей скоростью. Из-за этого давление в струе в этом месте оказывается меньше атмосферного, воздух из сосуда всасывается в струю через трубку В и удаляется вместе с водой.

Простейший пульверизатор состоит из двух трубок, расположенных перпендикулярно друг другу. Через горизонтальную трубку продувается воздух. В узкой части струи при выходе из трубки давление меньше атмосферного. Атмосферное давление поднимает жидкость по вертикальной трубке, и она распыляется струей воздуха.

3) Карбюратор – прибор, предназначенный для питания двигателя внутреннего сгорания горючей смесью.

Во время всасывающих тактов движения поршня двигателя наружный воздух проходит по трубе, которая имеет суженную часть – диффузор. В диффузоре помещен жиклер (распылитель воздуха) – трубка с малым отверстием. Жиклер соединен с поплавковой камерой карбюратора. При прохождении потока воздуха его скорость в диффузоре резко возрастает, давление становится меньше атмосферного и атмосферное давление выталкивает бензин из поплавковой камеры через жиклер. Бензин распыляется в потоке воздуха – образуется рабочая смесь, которая поступает в цилиндр двигателя.

Жидкости и газы существенно отличаются друг от друга. Различие между жидкостями и газами обусловлено большой сжимаемостью газов. Несмотря на это, явления в неподвижных жидкостях и газах аналогичны (закон Паскаля, закон Архимеда). При исследовании движения в жидкостях и газах эта аналогия во многом сохраняется, а именно: при движении газов со скоростями, значительно меньшими скорости звука (340м/с), сжимаемость газов достаточно мала и ее можно не учитывать. В связи с этим полученные ранее законы и утверждения можно применять и для газов.

Применим уравнение Бернулли для расчета подъемной силы крыла самолета.

При отсутствии сил сопротивления воздуха крыло обтекает ламинарный поток. Согласно уравнению Бернулли:

Если учитывать сопротивление воздуха, картина будет другая. Когда воздушный поток начинает обтекать крыло, то из-за действия сил трения у задней кромки образуется вихрь, в котором воздух вращается против часовой стрелки, если крыло движется влево. Применим уравнение Бернулли:

(т.к. вблизи точки 2 образуется вихрь) и .

Но по закону сохранения момента импульса при возникновении вращения против часовой стрелки должно возникнуть вращение по часовой стрелке.

Такое вращение воздуха и возникает вокруг крыла. На обтекающий крыло поток накладывается циркуляция воздуха вокруг крыла. В результате скорость воздушного потока над крылом оказывается больше, чем под крылом, так как над крылом скорость циркуляции имеет такое же направление, как и скорость набегающего на крыло потока, а под крылом эти скорости противоположны по направлению. Но согласно закону Бернулли давление должно быть больше там, где скорость меньше. Следовательно, под крылом самолета давление больше, чем над ним. Из-за этого и возникает подъемная сила.

и .

Известно, что наименьшая сила сопротивления действует на тело каплеобразной формы. Такая форма крыла самолета обеспечивает хорошую его обтекаемость.

Видео:Закон БернуллиСкачать

Задачи по гидродинамике (ЕГ)

Задачи по гидродинамике (гидравлика). Используют уравнение Бернулли. Встречаются в задачах ЕГ дополнительного уровня

Просмотр содержимого документа
«Задачи по гидродинамике (ЕГ)»

Задачи гидродинамика. Уравнение Бернулли

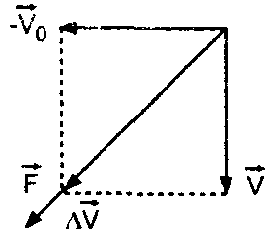
1) Направленная горизонтальная струя воды бьет в вертикальную стенку. С какой силой струя давит на стенку, если скорость истечения воды v = 10 м/с и вода поступает через трубку, имеющую сечение s = 4 см2? Считать, что после удара вода стекает вдоль стенки.

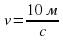
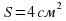
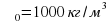
Дано F=?

Реш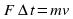

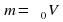
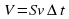
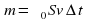
3). В сосуд, в дне которого узкое отверстие закрыт пробкой, налита вода до высоты h = 1 м. На поверхн воды находится поршень массой m = 1 кг и пло S = 100 см2. Между поршнем и стенками сосуда вода не просачивается. Найдите скорость истечения воды из отверстия в дне сосуда сразу после того, как из отверстия будет вынута пробка. Трение не учитывать.

Реш. Воспользуемся уравнением Бернулли. Давл в струе воды p0. Давл под порш на высоте h от отв p0 + mg/S. Скорость течения жидкости под поршнем м пренебречь, так как она мала по сравнению со скоростью истечения из отверстия , потому что площадь отверстия значительно меньше площади поршня. Согласно уравнению Бернулли

4) Брусок массы m удерживается в воздухе струями воды, бьющими вертикально вверх из отверстия, сечения S . Скорость воды на выходе из отверстия v. Достигнув бруска, вода разлетается от него в горизонтальной плоскости. На какой высоте над отверстием удерживается брусок? Плотность воды

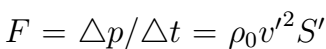
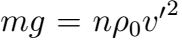
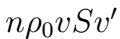
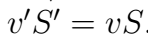
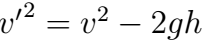
Реш Сила давления на брусок одной струи тогда

=т к из условия неразрывности струи следует, что из уравнения Бернулли имеем Решая совместно эти уравнения, получим

₁₎ Насос представляет расположенный горизонтально цилиндр с поршнем площади S и выходящим отверстием площади s, расположенном на оси цилиндра. Определить скорость истечения струи из насоса, если поршень под действ силы F перемещается с постоянной скоростью. Плотность жидкости . []

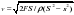
2) По наклонной плоскости стекает широкий поток воды. На расстоянии l по течению глубина потока уменьш вдвое. На каком расстоянии глубина потока уменьшится в 4 раза? [x = 5l]

_{6)по гориз}онт распол и изогнутой под прямым углом трубе сеч S течет жидкость плотности со скор V. C какой силой жидкость действует на трубу в месте изгиба если давление жидкости на выходе из трубы p? отв

_{Реш изменение импульса в единицу времени}

откуда

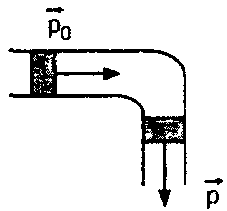
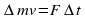
8) В широкий сосуд налита вода до высоты H. На поверхн воды налит слой масла плотности и высотой h. С какой скоростью вода начнет вытекать из сосуда, если на дне его обр отверстие? Понижением уровня воды в баке пренебречь. Плотность воды

10)В подводной лодке находящейся на глубине Н образовалась пробоина сечением S

.Какое количество воды нальется в лодку за время

Реш. Давление на одной глубине одинаково (по зну Паскаля), следовательно, снаружи давление жидкости p = ρgh. Чтобы удержать заплату, закрыв отверстие с внутренней стороны судна потребуется создать давление равное наружному p = F/S, Тогда, приравняв давления

F/S = ρgh и F = ρghS. Приняв плотность воды . имеем
F = 1,0 × 103 × 10 × 3 × 5,0 × 10−4 = 15 Н.

₇₎ Из крана выливается вода. Начиная с некоторого места, диаметр струи уменьшается на протяжении h от а до b Сколько воды вытечет из крана за время t? a=3см b=2см h=3см t=1 мин

Реш: Воспользуемся условием стационарности течения несжимаемой жидкости

Для идеальной жидкости уравнение Бернулли: .
Поскольку жид своб падает, то давл в обоих сеч одинак, и ур Бернулли прин вид: . За время t через любое сеч протекает один и тот же объем воды, поэтому . .Подставив полученное значение v₁ получим : .

2)На рис 3 2 манометра различной формы Найти разницу давлений показываемых этими манометрами если они поочередно измеряют давление в одной и той же трубе в которой течет вода со скоростью v

3)По гибкому шлангу сеч S течет жидкость плотн ρ со скор v. Найти натяж нити AB, соед концы A и B шланга, если изв, что она явл диам полуокружн, кот обр шланг (рис.).

4) Если полн открыт кран хол воды, а кран гор воды закрыт (рис.), то ванна наполн за t₁= 8 мин; если при этом на вых отв насад шланг с душем на конце, то время наполн увел до t₂ = 14 мин. Когда кран хол воды закрыт, а кран гор открыт полн, время наполн t₃ = 12 мин; при тех же усл, но с душем на конце − t₄ = 18 мин. За какое время наполн ванна, если полн отк оба крана? А если при этом насажен шланг с душем?

5) В дне бака высотой H=4см проделано отв пл 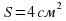Бак наполнен доверху при этом ур-нь постоянен из-за пополн из водоп. Какую подачу воды д обесп водопровод чтобы уровень в баке оставался неизменным? Коэф-т расхода от

РЕШ расход при истечении из малого отв скорость струи по ф-ле Торичелли

6)какую мощность должен иметь электродвигатель привода водяного насоса если насос при подаче создает напор H=40м а его полный кпд

Потребл мощ, т. е. мощн, кот на работу насоса затрач электродв (N_ЭД),= полезной мощн с учетом КПД: N_ЭД = N_П/η = ρgQH/η = 1000×9,81×0,05×40/0,6 = 32700 Вт = 32,7 кВт

7) Привод водян насоса обеспечивает частоту вращения его вала n₁ = 15 с -1 , при этом подача насоса Q₁ = 0,01 м 3 /с, а напор H₁ = 20 м. какова должна быть частотта вращения вала насоса, если потребуется увеличить его напор до 80 м. Как изменится при этом подача насоса?