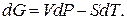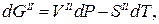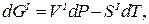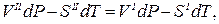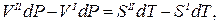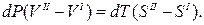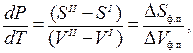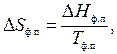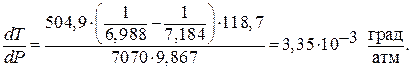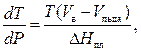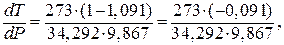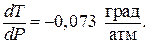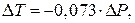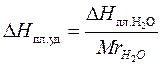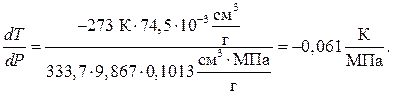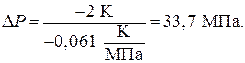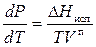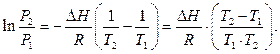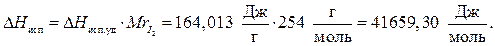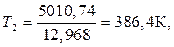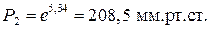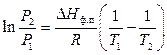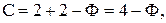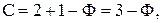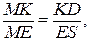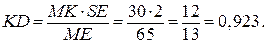Задачи на уравнение клапейрона клаузиуса (5 видео)

Содержание

Задачи на уравнение клапейрона клаузиуса
Уравнение Клапейрона – Клаузиуса
ВЫВОД И АНАЛИЗ УРАВНЕНИЯ КЛАПЕЙРОНА – КЛАУЗИУСА.
🎬 Видео

Видео:Физическая химия # 2. Вывод уравнения Клаузиуса-КлапейронаСкачать

Задачи на уравнение клапейрона клаузиуса

Для однокомпонентной системы (К=1) правило фаз записывается в виде

Если Ф = 1, то С =2 , говорят, что система бивариантна;
Ф = 2, то С =1 , система моновариантна;
Ф = 3, то С =0 , система нонвариантна.

Соотношение между давлением (р), температурой (Т) и объемом (V) фазы можно представить трехмерной фазовой диаграммой. Каждая точка (ее называют фигуративной точкой) на такой диаграмме изображает некоторое равновесное состояние. Обычно удобнее работать с сечениями этой диаграммы плоскостью р — Т (при V=const) или плоскостью р -V (при T=const). Разберем более детально случай сечения плоскостью р — Т (при V=const).

2.1. Фазовая диаграмма воды

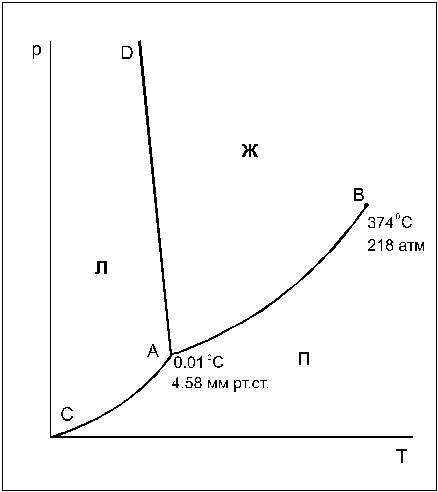
Фазовая диаграмма воды в координатах р — Т представлена на рис.1. Она составлена из 3 фазовых полей — областей различных (р,Т)-значений, при которых вода существует в виде определенной фазы — льда, жидкой воды или пара ( обозначены на рис.1 буквами Л, Ж и П, соответственно). Эти фазовые поля разделены 3 граничными кривыми.

Кривая АВ — кривая испарения, выражает зависимость давления пара жидкой воды от температуры (или, наоборот, представляет зависимость температуры кипения воды от давления). Другими словами, эта линия отвечает двухфазному равновесию (жидкая вода) D (пар), и число степеней свободы, рассчитанное по правилу фаз, составляет С = 3 — 2 = 1. Такое равновесие называют моновариантным. Это означает, что для полного описания системы достаточно определить только одну переменную — либо температуру, либо давление, т.к. для данной температуры существует только одно равновесное давление и для данного давления — только одна равновесная температура.

При давлениях и температурах, соответствующих точкам ниже линии АВ, жидкость будет полностью испаряться, и эта область является областью пара. Для описания системы в данной однофазной области необходимы две независимые переменные (С = 3 — 1 = 2): температура и давление.

При давлениях и температурах, соответствующих точкам выше линии АВ, пар полностью сконденсирован в жидкость (С = 2). Верхний предел кривой испарения AB находится в точке В, которая называется критической точкой (для воды 374 o С и 218 атм). Выше этой температуры фазы жидкости и пара становятся неразличимыми (исчезает четкая межфазная граница жидкость/пар), поэтому Ф=1.

Линия АС — эта кривая возгонки льда (иногда ее называют линией сублимации), отражающая зависимость давления водяного пара надо льдом от температуры. Эта линия соответствует моновариантному равновесию (лед) D (пар) (С=1). Выше линии АС лежит область льда, ниже — область пара.

Линия АD -кривая плавления, выражает зависимость температуры плавления льда от давления и соответствует моновариантному равновесию (лед) D (жидкая вода). Для большинства веществ линия АD отклоняется от вертикали вправо, но поведение воды

Рис.1. Фазовая диаграмма воды

аномально: жидкая вода занимает меньший объем, чем лед. На основании принципа Ле Шателье можно предсказать, что повышение давления будет вызывать сдвиг равновесия в сторону образования жидкости, т.е. точка замерзания будет понижаться.

Исследования, проведенные Бриджменом для определения хода кривой плавления льда при высоких давлениях, показали, что существует семь различных кристаллических модификаций льда, каждая из которых, за исключением первой, плотнее воды. Таким образом, верхний предел линии AD — точка D, где в равновесии находятся лед I (обычный лед), лед III и жидкая вода. Эта точка находится при -22 0 С и 2450 атм (см.задачу 11).

Тройная точка воды (точка , отражающая равновесие трех фаз — жидкости, льда и пара) в отсутствие воздуха находится при 0,0100 o С и 4,58 мм рт.ст. Число степеней свободы С=3-3=0 и такое равновесие называют нонвариантным.

В присутствии воздуха три фазы находятся в равновесии при 1 атм и при 0 o С. Понижение тройной точки на воздухе вызвано следующим причинами:
1. растворимостью воздуха в жидкой воде при 1 атм, что приводит к снижению тройной точки на 0,0024 o С;
2. увеличением давления от 4,58 мм рт.ст. до 1 атм, которое снижает тройную точку еще на 0.0075 o С.

2.2. Фазовая диаграмма серы

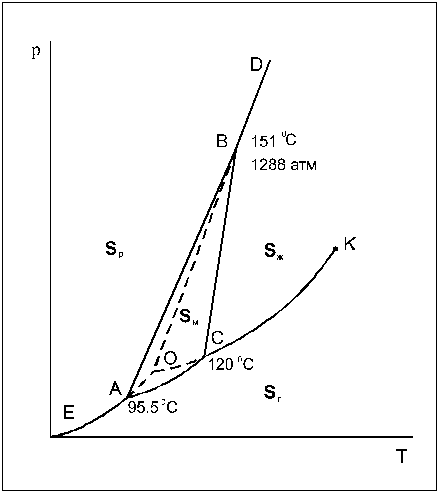
Кристаллическая сера существует в виде двух модификаций – ромбической (S_р) и моноклинной (S_м). Поэтому возможно существование четырех фаз: ромбической, моноклинной, жидкой и газообразной (рис.2). Сплошные линии ограничивают четыре области: пара, жидкости и двух кристаллических модификаций. Сами линии отвечают моновариантным равновесиям двух соответствующих фаз. Заметьте, что линия равновесия моноклинная сера — расплав отклонена от вертикали вправо ( сравните с фазовой диаграммой воды ). Это означает, что при кристаллизации серы из расплава происходит уменьшение объема. В точках А, В и С в равновесии сосуществуют 3 фазы (точка А – ромбическая, моноклинная и пар, точка В – ромбическая, моноклинная и жидкость, точка С – моноклинная, жидкость и пар). Легко заметить, что есть еще одна точка О,

Рис.2. Фазовая диаграмма серы

в которой существует равновесие трех фаз – перегретой ромбической серы, переохлажденной жидкой серы и пара, пересыщенного относительно пара, равновесного с моноклинной серой. Эти три фазы образуют метастабильную систему, т.е. систему, находящуюся в состоянии относительной устойчивости. Кинетика превращения метастабильных фаз в термодинамически стабильную модификацию крайне медленна, однако при длительной выдержке или внесении кристаллов-затравок моноклинной серы все три фазы все же переходят в моноклинную серу, которая является термодинамически устойчивой в условиях, отвечающих точке О. Равновесия, которым соответствуют кривые ОА, ОВ и ОС (кривые – возгонки, плавления и испарения, соответственно) являются метастабильными.

В случае диаграммы серы мы сталкиваемся с самопроизвольным взаимным превращением двух кристаллических модификаций, которые могут протекать в прямом и обратном направлении в зависимости от условий. Такого типа превращения называются энантиотропными (обратимыми).

Взаимные превращения кристаллических фаз, которые могут протекать лишь в одном направлении, называются монотропными (необратимыми). Примером монотропного превращения является переход белого фосфора в фиолетовый.

2.3. Уравнение Клаузиуса — Клапейрона

Движение вдоль линий двухфазного равновесия на фазовой диаграмме ( С=1 ) означает согласованное изменение давления и температуры, т.е. р=f(Т). Общий вид такой функции для однокомпонентных систем был установлен Клапейроном.

Допустим, мы имеем моновариантное равновесие (вода) D (лед) (линия AD на рис.1 ). Условие равновесия будет выглядеть так : для любой точки с координатами (р,Т), принадлежащей линии AD, _воды(р,Т) = _льда(р,Т). Для однокомпонентной системы =G/n, где G — свободная энергия Гиббса, а n — число молей (=const). Нужно выразить G=f(p,T). Формула G= H-T S для этой цели не годится, т.к. выведена для р,Т=const. В общем виде, Gє H-TS=U+pV-TS. Найдем дифференциал dG, используя правила для дифференциала суммы и произведения: dG=dU+p . dV+V . dp-T . dS-S . dT. Согласно 1-му закону термодинамики dU=dQ — dA, причем dQ=T . dS,a dA= p . dV. Тогда dG=V . dp — S . dT. Очевидно, что в равновесии dG_воды/n=dG_льда/n (n=n_воды=n_льда=сonst). Тогда v_{воды .} dp-s_{воды .} dT=v_{льда .} dp-s_{льда .} dT, где v_воды, v_льда — мольные (т.е. деленные на количество молей) объемы воды и льда, s_воды, s_льда — мольные энтропии воды и льда. Преобразуем полученное выражение в (v_воды — v_льда) . dp = (s_воды — s_льда) . dT, (10)

или: dp/dT= s_фп/ v_фп , (11)

где s_фп, v_фп — изменения мольных энтропии и объема при фазовом переходе ((лед) (вода) в данном случае).

Поскольку s_фп = H _фп/Т_фп, то чаще применяют следующий вид уравнения:

где H_фп — изменения энтальпии при фазовом переходе,
v_фп — изменение мольного объема при переходе,
Т_фп — температура при которой происходит переход.

Уравнение Клапейрона позволяет, в частности, ответить на следующий вопрос: какова зависимость температуры фазового перехода от давления? Давление может быть внешним или создаваться за счет испарения вещества.

Пример 6. Известно, что лед имеет больший мольный объем, чем жидкая вода. Тогда при замерзании воды v_фп = v_льда — v_воды > 0, в то же время H_фп = H_крист . v_фп) 0 С. Основываясь на этой закономерности, английские физики Тиндаль и Рейнольдс около 100 лет назад предположили, что известная легкость скольжения по льду на коньках связана с плавлением льда под острием конька; образующаяся при этом жидкая вода действует как смазка. Проверим, так ли это, используя уравнение Клапейрона.

Плотность воды — _в = 1 г/см 3 , плотность льда — _л = 1.091 г/см 3 , молекулярная масса воды — М = 18 г/моль. Тогда:

v_фп = М/ _в-М/ _л = 18/1.091-18/1= -1.501 см 3 /моль = -1.501 . 10 -6 м 3 /моль,

энтальпия плавления льда — Н_фп = 6.009 кДж/моль,

По уравнению Клапейрона:

dp/dT= — (6.009 . 10 3 Дж/моль)/(273К . 1.501 . 10 -6 м 3 /моль)=

= — 146.6 . 10 5 Па/К= -146 атм/К.

Значит, для плавления льда при температуре, скажем, -10 0 С необходимо приложить давление 1460 атм. Но такой нагрузки лед не выдержит! Следовательно, изложенная выше идея не соответствует действительности. Реальная же причина плавления льда под коньком — теплота, выделяемая при трении.

Клаузиус упростил уравнение Клапейрона в случае испарения и возгонки, предположив, что:

пар подчиняется закону идеального газа,
мольный объем жидкости v_ж (или v_тв) . H_исп)/(R . T 2 ), (12)

разделяя переменные получим:

dp/p=( H_исп/R) . (dT/T 2 ). (13)

Проинтегрируем левую часть в пределах от р₁ до р₂, а правую — от Т₁ до Т₂ (т.е. от одной точки (р₁,Т₁), лежащей на линии равновесия (жидкость) D (пар), до другой — (р₂,Т₂)):

(14)

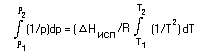
Результат интгерирования запишем в виде:

ln р₂ — ln р₁ = H_исп/R . (1/T₁ — 1/T₂) , (15)

называемым иногда уравнением Клаузиуса-Клапейрона. Оно может быть использовано для расчета теплоты испарения или возгонки, если известны значения давлений пара при двух различных температурах.

2.4. Энтропия испарения

Мольная энтропия испарения S_исп = H_исп/Т_кип равна разности S_пара — S_жидк. Поскольку S_пара >> S_жидк, то можно полагать S_исп S_пара. Следующее допущение состоит в том, что пар считают идеальным газом. Отсюда вытекает приблизительное постоянство мольной энтропии испарения жидкости при температуре кипения, называемое правилом Трутона.

Правило Трутона. Мольная энтропия испарения любой
жидкости составляет величину порядка 88 Дж/(моль . К).

Если при испарении разных жидкостей не происходит ассоциации или диссоциации молекул, то энтропия испарения будет приблизительно одинакова. Для соединений, образующих водородные связи (вода, спирты), энтропия испарения больше 88 Дж/(моль . К).

Правило Трутона позволяет определить энтальпию испарения жидкости по известной температуре кипения, а затем по уравнению Клаузиуса-Клапейрона определить положение линии моновариантного равновесия жидкость-пар на фазовой диаграмме.

Задача 2. Оцените давление пара над диэтиловым эфиром при 25 0 С, зная его температуру кипения ( 35.6 0 С ).

Решение: Согласно правилу Трутона S_исп = 88 Дж/(моль . К), с другой стороны S_исп= H_исп/T_кип; отсюда Н_исп=88 . (35.6+273)=27.16 кДж/моль ( по справочнику Н_исп=26.6 кДж/моль ).

Применим уравнение Клаузиуса-Клапейрона, учитывая, что при кипении (Т=308.6К) давление паров эфира р=1 атм. Тогда имеем ln p — ln 1 = 27.16 . 10 3 /8.31(1/308.6-1/T), или ln p = -3268/T + 10.59 ( и это является уравнением линии моновариантного равновесия (жидкость) (пар) на фазовой диаграмме эфира). Отсюда, при Т=298К (25 0 С) р=0.25 атм.

Энтропия плавления не так постоянна для разных веществ, как энтропия испарения. Это связано с тем, что беспорядок ( мерой которого является энтропия ) возрастает при переходе от твердого к жидкому состоянию не столь сильно, как при переходе в газообразное состояние.

Задачи на уравнение клапейрона клаузиуса

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору

Видео:Задачи на уравнение Менделеева-Клапейрона. Ч.1. Краткая теория + решение задачиСкачать

Уравнение Клапейрона – Клаузиуса

ТЕРМОДИНАМИКА

ЧАСТЬ II

кандидат технических наук, доцент кафедры ХТиЭ Дыблин Б.С.

(Березниковский филиал Пермского государственного технического университета)

Колбасина, В.Д.

К60 Термодинамика. Часть II. Фазовые равновесия. Термический анализ: учебно-метод. пособие / В.Д. Колбасина. – Березниковский филиал Пермского государственного технического университета. – Березники, 2011. – 53 с.

Пособие полностью соответствует программам по физической химии для студентов инженерного факультета и предназначено для приобретения навыков самостоятельной работы при решении задач, а также для подготовки к лабораторному практикуму.

Пособие дает представление о фазовых составляющих термодинамических систем и сущности термического анализа, поясняет термины, используемые при их определении и основные принципы метода термического анализа термодинамических систем. В нем приводятся примеры решений примеров термодинамического равновесия и термического анализа, а также с построением диаграмм плавкости. Даются примеры оформления и выполнения расчетных работ.

Предназначено для студентов, изучающих курс «Физическая химия».

технический университет», 2011

Оглавление

1. Уравнение Клапейрона – Клаузиуса. 4

1.2. Испарение (сублимация) 9

2. Термодинамическое равновесие. Правило фаз Гиббса. 12

2.1. Диаграмма состояния воды в области средних давлений. 16

3. Двухкомпонентные системы.. 18

3.1. Системы с полной нерастворимостью компонентов в твердом состоянии 20

3.1.1. Неизоморфные двухкомпонентные системы с простой эвтектикой 20

3.1.2. Неизоморфные двухкомпонентные системы, образующие устойчивое химическое соединение. 29

3.1.3. Неизоморфныне двухкомпонентные системы, образующие два новых химических соединения. 31

3.1.4. Неизоморфные двухкомпонентные системы, образующие неустойчивое химическое соединение. 32

3.2. Изоморфные системы (системы с твердыми растворами) 36

4. Трехкомпонентные системы.. 43

5. Термический анализ. 47

5.1. Экспериментальная часть. 51

Библиографический список. 52

Уравнение Клапейрона – Клаузиуса

Процессы, заключающиеся в превращении одной фазы вещества в другую того же вещества, протекающие без химических реакций, называются фазовыми превращениями (плавление, возгонка, испарение, полиморфные превращения).

Когда система, состоящая из нескольких фаз, достигает равновесия, то переход молекул из одной фазы в другую не прекращается. Например, в равновесной системе вода – пар молекулы все время переходят из жидкости в пар и обратно. Для равновесия характерно равенство скоростей испарения и конденсации. Равновесие, таким образом, поддерживается двумя противоположными процессами, идущими с одинаковыми скоростями.

Фазовые равновесия, разумеется, могут устанавливаться и в других системах, например, в системах жидкость – твердое тело, или твердое тело –газ и др.

Состояние равновесия при постоянном Р и Т термодинамически характеризуется равенством энергий Гиббса одной и другой фазы: 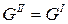, т.е. изобарно-изотермические потенциалы чистого вещества в двух фазах находящихся в равновесии, при равенстве молекулярных весов равны между собой.

При изменении энергии Гиббса одной фазы для сохранения равновесия в системе меняется энергия Гиббса другой фазы на ту же величину, т.е.

или .

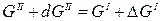
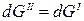
Изменение изобарно-изотермического потенциала DG может происходить только за счет изменения Р и Т, т.к. G = ƒ (P, T).

Эта зависимость выражается в общем виде уравнением

Следовательно, для двух смежных фаз, находящихся в равновесии запишем

так как 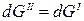(условие равновесия), то

где S I и S II – энтропия 1-го моля вещества в первой и во второй фазах;

V I и V II – объем 1-го моля вещества в первой и во второй фазах;

– температурный коэффициент изменения давления насыщенного

– энтропия фазового перехода,

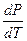
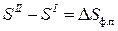
где DН_ф.п. – энтальпия фазового перехода;

Т_ф.п. – температура фазового перехода.

Тогда уравнение примет вид

. (1)

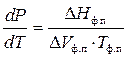
Эта зависимость была найдена Клапейроном еще до открытия первого закона термодинамики, а затем выведена Клаузиусом. Уравнение (1) называют уравнением Клапейрона – Клаузиуса в дифференциальной форме. Оно является общим термодинамическим уравнением, применимым ко всем фазовым переходам чистых веществ (однокомпонентных систем), т.е. к процессам плавления (равновесие твердое тело – жидкость), испарения (равновесие жидкость – пар), сублимации (равновесие твердое тело – пар), полиморфного превращения (равновесие их форм), а также и обратным им процессам.

Уравнение Клапейрона – Клаузиуса можно применить к любому количеству вещества, отнеся экстенсивные величины (DН и DV) к одинаковому его количеству. Обычно эти величины относят или к молю или к грамму.

Для того чтобы воспользоваться им для нахождения одной из зависимостей, надо знать три остальные. Например, чтобы найти зависимость давления насыщенного пара от температуры, надо знать зависимость теплоты фазового перехода (DН_ф.п) от температуры и зависимость мольных объемов равновесных фаз (V I – V II ) от температуры.

Рассмотрим применимость уравнения Клапейрона – Клаузиуса к фазовым переходам (плавление, испарение, сублимация), представляющим наиболее общий интерес.

Плавление

Решение.

Определим изменение температуры плавления при повышении давления на 1 атм, т.е. .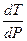

Из уравнения Клапейрона – Клаузиуса

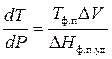
В соответствии с условием здесь:

Т_ф.п – температура плавления под давлением 1 атм;

DV – разность объемов (удельных) жидкого и твердого олова;

DН_ф.п.уд – удельная теплота плавления олова.

Для нашего случая

, тогда , .

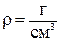
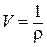
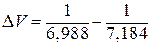
В условии задачи дана молярная теплота плавления. Ее необходимо перевести в удельную теплоту плавления, так как М_r (Sn) = 118,7 г/моль, то

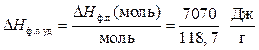
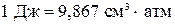
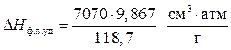
Учитывая, что , то

После подстановки получаем:

Это значит, что при повышении давления на 1 атм температура плавления олова увеличится на 3,35∙10 -3 град.

Температура плавления олова под давлением 100 атм будет равна

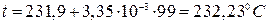
Пример 2.Удельный объем (V) льда при 0 0 С равен 1,091 см 3 /г, а воды 1 см 3 /г. Теплота плавления льда равна 34,292 Дж/г. Как изменится Т_пл льда при изменении давления на 1 атм? При какой температуре плавится лед под давлением собственного насыщенного пара 4,6 мм.рт.ст?

Решение.

Воспользуемся уравнением Клапейрона – Клаузиуса. Надо определить

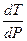
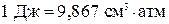
так как имеет размерность град/атм, а величина (V_в – V_льда) см 3 /г, то величина DН_пл должна быть выражена в атм·см 3 /г. Учитывая, что , то получаем

Следовательно, если давление возрастает на 1 атм, температура плавления понижается на 0,073 0 С.

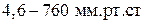
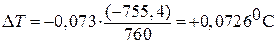
Если давление уменьшается с 1 атм до 4,6 мм.рт.ст ( ), то

– температура плавления повысится на 0,0726 0 С.

Пример 3. Под давлением 0,1013 МПа лед плавится при температуре 273К. Удельный объем льда при 273К равен 991,1∙10 -3 см 3 /г, а воды – 916,6∙10 -3 см 3 /г. Молярная теплота плавления льда равна 6010 Дж/моль. Вычислить давление, при котором лед будет плавиться при 271К.

Решение.

Воспользуемся уравнением Клапейрона – Клаузиуса:

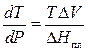
где DV = V_ж – V_т = 916,6 ∙ 10 -3 – 991,1 ∙ 10 -3 = –74,5 ∙ 10 -3 см 3 /г – знак минус показывает, что при плавлении льда объем системы уменьшается;

DН_пл – теплота плавления. В задаче дана молярная теплота плавления. Необходимо перевести в удельную теплоту плавления.

Мr (Н₂О) = 18,01 г/моль, тогда

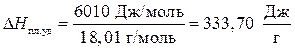
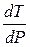
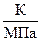
но для зависимости единицы измерения – , и 1Дж = 9,867см 3 ∙атм. Или 1 Дж = 9,867 ∙ 0,1013 см 3 МПа.

Тогда DН_пл = 333,70 ∙ 9,867 ∙ 0,1013 .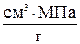

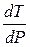
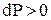
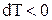
Отрицательное значение зависимости показывает, что при увеличении давления ( ) температура плавления льда понижается ( ).

Давление, при котором лед будет плавиться при 271К найдем из уравнения (3) .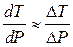

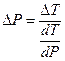
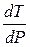
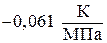
Отсюда , но DТ = (271–273) К = – 2К, а рассчитано ранее ( ), таким образом

Следовательно Р = Р₀ + DР = 0,1013 + 33,7 = 33,8 (МПа) – при давлении 33,8 МПа лед будет плавиться при 271К.

Испарение (сублимация)

При умеренных температурах и давлениях, ни слишком близких к критическим, объем кипящей жидкости мал по сравнению с объемом сухого насыщенного пара, поэтому изменение объема DV = V п – V ж в уравнении Клапейрона – Клаузиуса может быть заменено объемом V П – сухого насыщенного пара. Уравнение Клапейрона – Клаузиуса в этом случае примет вид

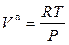
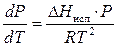
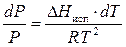
Если при умеренных давлениях к сухому насыщенному пару применимо уравнение состояния идеального газа PV = RT, заменим и тогда

На основе рассуждений может быть получено уравнение Клапейрона –Клаузиуса для процесса сублимации, которое является приближенным. Преимущество его состоит в простоте, с которой оно может быть проинтегрировано

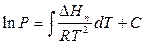
На диаграмме в координатах ln P – 1/T это уравнение выражается прямой линией с тангенсом угла наклона к оси 1/Т, равным – .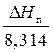

Это обстоятельство может быть использовано для нахождения примерного значения средней молярной теплоты парообразования (сублимации) в определенном интервале температур.

Интегрирование приближенного уравнения Клапейрона – Клаузиуса в предположении, что DН не зависит от Т в пределах Р₁ – Р₂ дает

Это уравнение приемлемо для использования в небольшом интервале температур.

Пример 1. Нормальная температура кипения йода 185 0 С. Теплота парообразования DН_исп.уд = 164,013 Дж/г. До какой примерно температуры следует нагреть йод в аппарате, в котором поддерживается давление 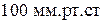, чтобы обеспечить перегонку?

Решение.

Воспользуемся уравнением Клапейрона – Клаузиуса

. (4)

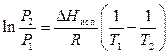
В уравнении дана молярная теплота испарения (DН_исп), а в условии задачи удельная теплота парообразования, но

Переведем t 0 C в Т К. Т = 185 0 С + 273 = 458К.

Подставим имеющиеся данные в уравнение (4) и решим относительно Т₂.

;

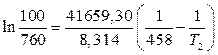
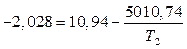
t 0 С = 386,4 – 273 = 113,4 0 С.

Вывод. При давлении равном 100 мм.рт.ст йод закипит при температуре 113,4 0 С.

Пример 2. При атмосферном давлении диэтиламин кипит при 58 0 С. Под каким давлением будет кипеть диэтиламин при 20 0 С, если нормальная теплота парообразования 27844,52 Дж/моль?

Решение.

Воспользуемся уравнением Клапейрона – Клаузиуса

. (4)

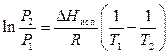
Переведем t 0 C в Т К.

Подставим данные в уравнение (4) и решим относительно Р₂.

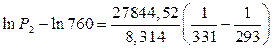
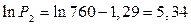
Вывод. При давлении равном 208,5 мм.рт.ст. диэтиламин будет кипеть при 20 0 С.

Пример 3. Давление паров кристаллического ацетилена при 132К равно 1,7 мм.рт.ст, а при 153К – 27,6 мм.рт.ст. Рассчитать мольную теплоту плавления ацетилена, если удельная теплота парообразования его составляет 828,014 Дж/г.

Решение.

По условию ацетилен из твердого состояния переходит в парообразное, т.е. DН_ф.п = DН_пл + DН_исп. Воспользуемся уравнением (4) Клапейрона –Клаузиуса:

и решим относительно DН_ф.п,

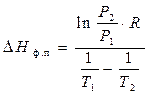
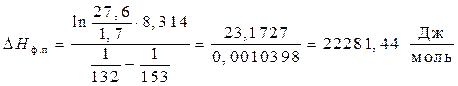
В задаче дана удельная теплота испарения. Ее необходимо перевести в мольную теплоту испарения, так как Мr(С₂Н₂) = 26 г/моль

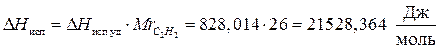
DН_пл = 22281,44 – 21528,364 = 753,056 .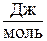

Вывод. Молярная теплота плавления ацетилена равна 753,056 .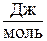

Двухкомпонентные системы

Изучение взаимодействия веществ в многокомпонентных системах без выделения образующихся продуктов проводится методом физико-химического анализа, сущность которого заключается в исследовании зависимости между численными значениями физических свойств равновесной химической системы и концентрациями компонентов, определяющих состояние равновесия.

На основании изучения физических свойств равновесной системы строятся диаграммы в координатах состав – свойство. По геометрическим особенностям диаграмм, по совокупности линий, поверхностей и т.д. можно наглядно судить не только о химической природе образующихся веществ, но и о числе, границах устойчивости, условиях совместного существования разных фаз в системе.

Основы этого метода заложены Д.И. Менделеевым, Ле-Шателье, Г. Тамманом, всесторонне развиты Н.С. Курнаковым, и нашли широкое применение в производстве стали, других сплавов, в галургии и производстве силикатных материалов.

Рассмотрим двухкомпонентные конденсированные системы, где присутствуют жидкие и твердые фазы.

Правило фаз Гиббса выразится в этом случае формулой:

но в таких системах обычно давление остается постоянным (Р = const) поэтому число свободных переменных становится равным 1 и тогда

т.е. такую диаграмму состояния можно построить на плоскости, выразив зависимость состав – температура.

Такие диаграммы получают методом термического анализа. Сущность этого метода состоит в том, что расплавленную смесь двух веществ охлаждают, измеряя через равные промежутки времени температуру и в координатах время – температура строят кривую охлаждения, используя тот факт, что пока в охлажденной системе не происходит никаких изменений (превращений), температура падает практически с постоянной скоростью. Процессы, сопровождающиеся выделением теплоты (кристаллизация, химические реакции, полиморфные превращения и т.д.), отражаются на кривой охлаждения или изломом (участок с замедленной скоростью охлаждения) или горизонтальными участками с постоянной температурой, что изображено на рис. 2.

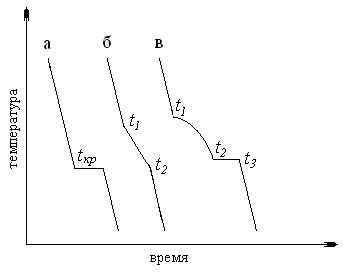
Рис. 2. Типы кривых охлаждения:

а – чистое вещество;

б – смесь изоморфных веществ;

в – смесь неизоморфных веществ

Характерные точки на кривых охлаждения:

§ Кривая а: t_кр – температура кристаллизации чистого вещества. Длительность температурной остановки и тем самым размер горизонтального участка на кривой охлаждения зависят от количества вещества и от скорости отвода тепла. При исчезновении последней капли жидкости температура начинает понижаться.

§ Кривая б: t₁ – температура начала кристаллизации изоморфной системы, t₂ – температура конца кристаллизации изоморфной системы.

§ Кривая в: t₁ – температура начала кристаллизации одного компонента неизоморфной системы, t₂–t₃ – температура начала и конца кристаллизации эвтектической смеси. При охлаждении расплава двухкомпонентной системы отвердевание начинается с кристаллизации того из компонентов, относительно которого жидкий расплав становится насыщенным. На кривых охлаждения б и в, показано, что в точке t₁ начало кристаллизации одного из компонентов приводит к излому кривой и к понижению скорости охлаждения, вследствие выделения теплоты кристаллизации. Отсутствие температурной остановки объясняется тем, что состав жидкой фазы при кристаллизации меняется. При достижении температуры, при которой жидкий раствор становится насыщенным относительно и второго компонента, происходит одновременная кристаллизация обоих компонентов, на кривой охлаждения появляется еще один излом (t₂). При этом состав жидкой фазы остается постоянным. Поэтому на кривой охлаждения наблюдается температурная остановка (t₂–t₃). После отвердевания всей смеси (t₃) температура снова понижается.

Следовательно, всякий излом на кривой охлаждения указывает на начало некоторого превращения.

Чтобы получить диаграмму состояния, вначале экспериментально получают кривые охлаждения для ряда смесей с различной известной концентрацией компонентов А и В и на их основе уже строят диаграмму состояния системы А–В. Для этого на координатную сетку состав –температура наносят все температурные остановки и точки излома на кривых охлаждения, а потом соединяют полученные точки.

Рассмотрим основные диаграммы равновесных двухкомпонентных конденсированных систем.

Решение.

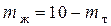
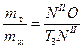
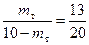
Дана общая масса системы (10 кг), следовательно, . Согласно правилу рычага замеряем отрезки N II O и Т₃N II и получаем решаем уравнение 33 m _т = 130 Þ m _т = 3,94 кг.

Вывод: при охлаждении 10 кг смеси состава n до температуры Т₃ выделится 3,94 кг кристаллов А.

В точке N III начинают выпадать первые кристаллы вещества В, следовательно, в системе находятся 3 фазы: одна жидкая (расплав состава n_Е) и две твердые (кристаллы А и кристаллы В), т.е. , тогда , система безвариантна. Значение показывает, что эти три фазы могут находиться в равновесии только при вполне определенных условиях, когда температура равна эвтектической температуре (Т_Е), а раствор имеет эвтектический состав (n_Е). Ни температуру, ни состав невозможно в этом случае изменить, не изменив число и вид фаз. Согласно закону фазового равновесия Гиббса, кристаллизация эвтектики из раствора должна происходить при постоянной температуре, кроме того, соотношение масс кристаллов А и В в выпавшей эвтектике должно быть таким же, как и массовое содержание веществ А и В в расплаве эвтектического состава.

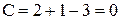
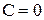
В связи с тем, что кристаллы А и В при кристаллизации эвтектики выпадают одновременно и у них нет условий для роста кристаллов, твердая эвтектика имеет мелкокристаллическую структуру. Застывший расплав состава N III (ниже температуры Т_Е) состоит из сравнительно крупных кристаллов А, которые выпали в интервале температур между точками N I и N III и мелкокристаллической смеси кристаллов А и В твердой эвтектической смеси.

Процесс кристаллизации заканчивается в фигуративной точке N III при температуре Т_Е полным застыванием жидкого раствора (расплава).

После исчезновения жидкой фазы в системе остаются только две фазы: кристаллы А и кристаллы В. Это значит, что произвольно может меняться только температура.

В точке N IV продолжается охлаждение двух твердых фаз.

Кривая охлаждения для рассмотренного случая будет выглядеть так (см. рис. 3 — III).

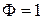
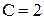
Участок N – N I : , , охлаждение идет равномерно по закону Ньютона.

Участок N I -N II : в т. N I наблюдается излом, что говорит о появлении новой фазы – начинает кристаллизоваться вещество А. Кривая охлаждения опускается более полого, чем на участке N – N I . Это объясняется тем, что при кристаллизации вещества А из расплава выделяется теплота, которая замедляет педение температуры, следовательно, , .

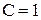
При дальнейшем охлаждении температура понижается до эвтектической температуры Т_Е, система достигает фигуративной точки N III , при этом состав жидкой фазы в точке Е становится эвтектическим и начинается выпадение твердой эвтектики, т.е. смеси кристаллов А и В. (кр А + кр В + Ж), следовательно . N III – начало кристаллизации эвтектики, N IV – конец кристаллизации эвтектики.

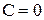
Треугольник Таммана

Если рассматривать кривые охлаждения смесей двухкомпонентной неизоморфной системы 2, 3, 4, 6 (см. рис. 3 – I), то можно отметить, что каждая из них имеет два излома.

Первый излом указывает на появление новой фазы – это начало кристаллизации чистого компонента (для кривых охлаждения 2, 3, 4 – это начало выделения кристаллов А, для кривой охлаждения 6 – это начало выделения кристаллов В).

Второй излом, переходящий в горизонтальный отрезок, характеризует начало кристаллизации эвтектики.

На кривых охлаждения размеры этих отрезков (а, б, в, г, д) различны. Они прямо пропорционально зависят от количества выпавшей эвтектики. В нашем примере самый большой отрезок г (ЕМ) находится на кривой охлаждения 5 (состав: 30% А и 70% В), которая имеет всего один излом, переходящий в горизонтальную площадку. Это говорит о том, что мы имеем дело изначально с эвтектической смесью, чем объясняется большой размер г.

Если на диаграмме отложить отрезки (а, б, в, г, д) от линии солидуса и соединить полученные точки между собой, то образуется треугольник Т_ЕFM– треугольник Таммана, он позволяет рассчитать массу эвтектической смеси, которая выпадает при охлаждении системы любого состава АВ.

Пример. Пусть изначально взято 5 кг смеси состава 70% А и 30% В. Определить сколько эвтектики выделится при охлаждении данной смеси.

Решение.

Рассмотрим два треугольника. Треугольник Т_ЕN III N IV подобен треугольнику Т_ЕЕМ, из чего вытекает

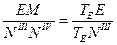
где ЕМ – 5кг, а отрезки Т_ЕЕ и Т_ЕN III замеряем.

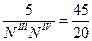
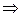
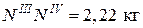
Вывод: при охлаждении 5 кг смеси состава 70% А и 30% В выделиться 2,22 кг эвтектической смеси.

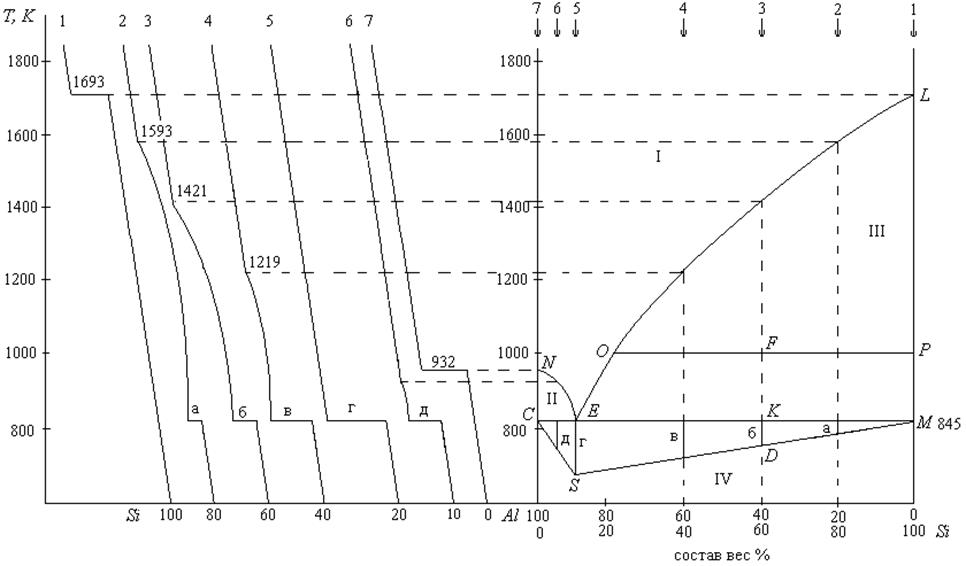
Задача. На основании кривых охлаждения системы алюминий – кремний (рис. 4) построить диаграмму состав – температура плавления. По диаграмме определить:

1. При какой температуре начнется кристаллизация системы, содержащей 60% кремния?

2. Какой элемент будет переходить в твердое состояние?

3. Какое количество твердой фазы будет образовано при охлаждении до 1000К 2 кг системы, содержащей 60% кремния?

4. При какой температуре кристаллизация закончится?

5. Определить состав последней капли жидкости.

6. Найти массу эвтектики при охлаждении 2 кг смеси, содержащей 60% кремния.

Решение.

На основании кривых охлаждения строим диаграмму состав – температура. При кристаллизации чистого кремния (кривая охлаждения 1) наблюдается температурная остановка при 1693К (температура плавления кремния). Эту температуру откладываем на оси температур, отвечающей чистому кремнию (L).

На кривой 2, содержащей 80% кремния, при 1593К обнаруживается уменьшение скорости охлаждения. При этом начинает выпадать чистый кремний в виде кристаллов, а жидкая фаза обогащается алюминием. При увеличении содержания алюминия, температура плавления системы уменьшается. При 845К на кривой 2 наблюдается температурная остановка (горизонтальная площадка — а), после чего вся система переходит в твердое состояние. При этом одновременно выпадают в виде кристаллов и алюминий, и кремний, т.е. кристаллизуется эвтектика. Оба вида кристаллов хорошо различимы под микроскопом.

При охлаждении системы, содержащей 40% кремния (кривая 4) изменение скорости охлаждения наблюдается уже при 1219К, а горизонтальная площадка (в) наблюдается при той же температуре, что и на кривой 2 (845К), что указывает на кристаллизацию эвтектики, а так как состав эвтектики постоянен, то длина горизонтальной площадки пропорциональна количеству кристаллизующейся эвтектики.

При охлаждении системы, содержащей 10% кремния (кривая охлаждения 5) наблюдается температурная остановка при 845К. Длина горизонтальной площадки (г) максимальна на кривой 5, что означает, что система, содержащая 10% кремния, соответствует эвтектическому составу.

При охлаждении чистого алюминия (кривая 7) наблюдается температурная остановка при 932К, что соответствует температуре плавления чистого алюминия.

Закончив построение диаграммы по всем кривым охлаждения, получим две кривые ликвидуса (NE, EL) и горизонтальную прямую солидуса СЕМ, которые пересекаются в одной, так называемой эвтектической точке Е.

Выше кривых NEL (зона I) система находится в жидком состоянии.

Рис.4. Диаграмма состояния алюминий — кремний

В зоне II сосуществуют кристаллы алюминия и расплав, состав которого при каждой температуре определяется по кривой NE.

В зоне III сосуществуют кристаллы кремния и расплав, состав которого определяется по кривой ЕL.

В зоне IV система находится в твердом состоянии. Так как длина горизонтальной площадки, соответствующая кристаллизации эвтектики, пропорциональна количеству эвтектики, то это можно использовать для определения массы эвтектики, которая может быть выделена из смеси любого состава. Для этого необходимо построить треугольник Таммана.

Длины горизонтальных площадок (а, б, в, г, д) откладывают вертикально вниз от СЕМ в точках, отвечающих составам смесей. Соединив нижние концы и точки С и М, получаем треугольник Таммана.

1. Кристаллизация смеси, содержащей 60% кремния, начнется при температуре 1421К.

2. В твердую фазу будет переходить кремний. Расплав будет обогащаться алюминием.

3. При охлаждении системы, содержащей 60% кремния до 1000К, некоторое количество кремния выделится в виде кристаллов. Для определения количества твердой и жидкой фаз применяется правило рычага.

Вес кристаллов кремния так относится к весу жидкой фазы, как отрезок OF относится к отрезку FP. Если вес системы 2 кг, то

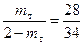
решаем уравнение относительно m_т:

При Т = 1000К из системы, содержащей 60% кремния, выделится 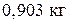кристаллического кремния.

4. Кристаллизация этой смеси закончится при температуре 845К – температуре эвтектики.

5. Состав последней капли жидкости соответствует составу эвтектики (10% кремния и 90% алюминия).

6. Массу эвтектики определяем из треугольника Таммана. Треугольник MKD подобен треугольнику MES, следовательно:

по условию m_{системы} = 2 кг => ES = 2, все отрезки замеряем,

При охлаждении 2 кг смеси, содержащей 60% кремния, выделится 0,923 кг эвтектики.

Решение.

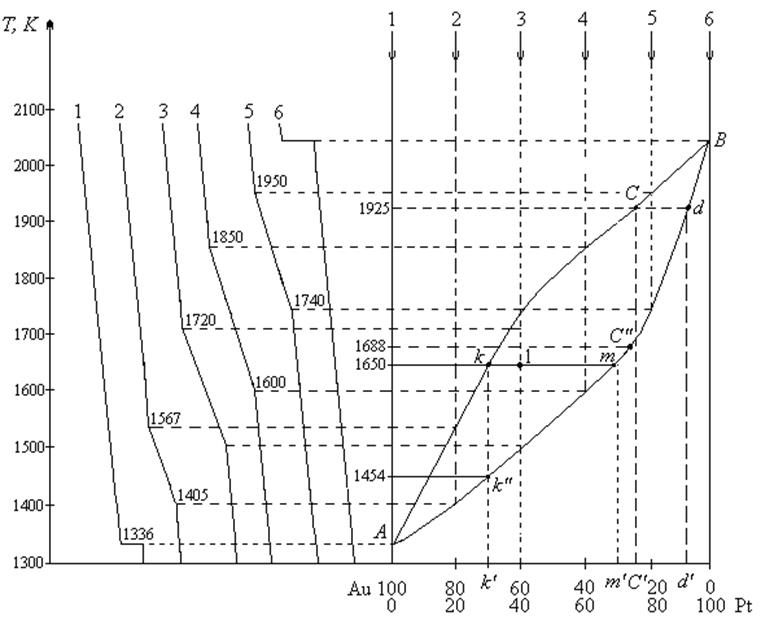
На основании кривых охлаждения строим диаграмму плавкости (рис. 9).

Кривая 1 соответствует охлаждению чистого золота. При Т = 1336К на кривой наблюдается температурная остановка. Она соответствует температуре плавления золота. Чистые вещества кристаллизуются при постоянной температуре, пока жидкая фаза не превратится в твердую. На оси ординат откладываем точку (1336), соответствующую температуре плавления золота.

Кривая 2 соответствует охлаждению системы, состоящей из 20% Pt и 80% Au. При Т = 1567К на кривой охлаждения наблюдается некоторый излом (скорость охлаждения уменьшается). Это объясняется выделением теплоты при кристаллизации смеси. При Т = 1405К заканчивается кристаллизация. Тепло больше не выделяется, поэтому некоторый излом на кривой 2 при этой температуре говорит о некотором увеличении скорости охлаждения (просто идет охлаждение полученной твердой системы).

Рис. 9. Диаграмма состояния изоморфной системы золото – платина

На оси ординат, соответствующей составу 20% Pt и 80% Au, откладываем Т = 1567К (температуру начала кристаллизации) и Т = 1405К (температуру конца кристаллизации). Аналогично находим точки, отвечающие другим составам. Соединив эти точки, получим две кривые АkСВ – линия ликвидуса и AmdB – линия солидуса, сходящиеся в точках плавления чистых веществ, которые представляют диаграмму изоморфной двухкомпонентной системы.

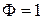
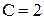
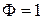
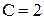
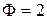
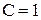
Выше линии ликвидуса вся система находится в жидком состоянии ( , ), ниже солидуса – в твердом состоянии ( , ). Между кривыми АkСВ и AmdB часть системы находится в жидком состоянии, а часть перешла в твердое состояние ( , ) – область равновесного сосуществования жидких и твердых растворов. Количество веществ, находящихся и жидком и твердом состоянии, определяется по правилу рычага.

1. Кристаллизация системы, содержащей 75% Pt и 25% Au (С’), начнется при Т = 1925К.

2. Кристаллизация закончится, когда состав твердой фазы будет равен составу исходной жидкой фазы, т.е при 1688К (С»).

3. Состав первого кристалла определяется по точке пересечения изотермы начала кристаллизации с линией солидуса (d), которой соответствует состав d’.

4. Система, содержащая 40% Pt и 60% Au, при охлаждении до 1650К гетерогенна – состоит из жидкой фазы состава k’ и кристаллов состава m’. Массу кристаллов и жидкой фазы определяем по правилу рычага: вес твердой фазы относится к весу жидкой фазы как плечо kl относится к плечу lm, т.е.

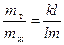
Общий вес смеси 1,5 кг, и если принять, что х – масса твердой фазы (кристаллов), то (1,5 — х) – масса жидкой фазы. Измерив длину плеч kl и lm, определим х

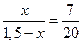
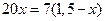
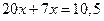
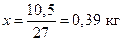
Следовательно, при Т = 1650К выпадет 0,39 кг кристаллов, содержащих 70% Pt и 30% Au (m’), и остается 1,5 – 0,39 = 1,11 кг жидкой фазы состава 30% Pt и 70% Au (k’).

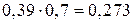
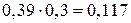
В твердой фазе (кристаллов) содержатся кг Pt и кг Au.

Состав жидкой фазы: Pt 1,11 × 0,3 = 0,333 кг, Au 1,11 × 0,7 = 0,777 кг.

5. Система полностью закристаллизуется при Т = 1454К, и состав последней капли будет равен k’ (т.е. 30% Pt и 70% Au).

Пример 2.

Воспользовавшись диаграммой плавкости системы железо – ванадий (рис. 10) определить:

1) число степеней свободы системы в точках а, b, с, d;

2) указать в каких пределах изменяется состав жидкого и твердого растворов при затвердевании 60%-ного сплава;

Видео:Успеть за 300 секунд, #3: Уравнение Клапейрона-МенделееваСкачать

ВЫВОД И АНАЛИЗ УРАВНЕНИЯ КЛАПЕЙРОНА – КЛАУЗИУСА.

ТЕПЛОВЫЕ ЭФФЕКТЫ ФАЗОВЫХ ПЕРЕХОДОВ.

УРАВНЕНИЕ КЛАПЕЙРОНА – КЛАУЗИУСА.

Переход компонента из одной фазы в другую сопровождается выделением или поглощением теплоты, которую можно определить количественно на основе фундаментального уравнения термодинамики:

(*)

ВЫВОД И АНАЛИЗ УРАВНЕНИЯ КЛАПЕЙРОНА – КЛАУЗИУСА.

Для любого равновесного перехода вещества из одной фазы α в другую фазу β, применяя уравнение (*) к каждой из фаз, можно написать

Индексы α и β отражают принадлежность параметров к соответствующей фазе. В равновесных условиях между фазами α и β изменение энергии Гиббса отсутствует, т.е.

Приравнивая правые части уравнений 1 и 2, получим

Для равновесного обратимого процесса согласно уравнениям и запишем

а уравнение (3) примет вид

где ∆H_пер – теплота фазового перехода.

Тепловой эффект, сопровождающий фазовый переход, определяется следующим образом:

уравнение

где ∆V – изменение объема в результате фазового перехода; dP/dT – изменение давления в зависимости от температуры при сохранении равновесия между двумя фазами.

Уравнение Клапейрона–Клаузиуса связывает тепловой эффект процесса с изменением давления насыщенного пара, температурой и изменением объема в процессе фазового перехода.

Для процессов испарения ж→п и сублимации тв→п уравнение Клапейрона–Клаузиуса можно представить следующим образом:

где ∆H_исп , ∆H_суб – теплоты испарения и сублимации; V_п, V_ж, V_тв – мольные объемы пара, жидкости и твердого тела соответственно.

В процессе испарения и сублимации наблюдается значительное изменение удельного объема ∆V и существенное изменение величины dP/dT. При плавлении, напротив, изменение ∆V невелико, и величина dP/dT незначительна.

Пример 1. Проведем расчет по уравнению Клапейрона–Клаузиуса температуры плавления фенола Т_пл. Плотность твердого фенола ρ_тв при атмосферном давлении составляет 1,072∙10 3 кг/м 3 , а жидкого ρ_ж = 1,056∙10 3 кг/м 3 ; теплота плавления ∆H_пл = 1,045∙10 5 Дж/кг; температура замерзания 314,2 К. Определим dP/dT и температуру плавления при Р = 5,065∙10 7 Па:

Прирост температуры плавления при повышении давления на 1 атм ( 1,013∙10 5 Па) составляет 4,525∙10 -8 град/Па. При увеличении давления до 5,065∙10 7 Па температура плавления увеличивается на ∆T = (dT/dP)∆P = 4,525∙10 -8 ∙ 5,065∙10 7 = 2,29 К, т.е. составит Т_пл = 314,2+2,29 = 316,49 К.

Следует иметь в виду, что в процессе плавления у большинства веществ V_ж > V_{тв ,} тогда ∆V>0 и при повышении давления Р↑ температура плавления повышается Т↑.

Однако, такие вещества как вода (Н₂О), висмут (Bi), имеют объем твердой фазы V_тв больше, чем объем жидкой фазы V_ж уд = 10 -3 м 3 /кг и V_тв уд = 1,091·10 -3 м 3 /кг; теплота плавления ∆H_пл = 332,4 кДж/кг:

Это значение показывает, что для понижения температуры таяния льда на один градус Кельвина необходимо увеличить давление на 1,34∙10 7 Па, т.е. примерно на 134 атмосферы, что нереально, поскольку такое давление лед не выдерживает – трескается.

Таяние льда происходит в основном в результате трения и превращения работы в теплоту при скольжении конька по льду, а не за счет повышения давления на лед.

Уравнение для процесса испарения можно представить в интегральном виде. Мольный объем пара значительно превосходит мольный объем жидкости, V_п >> V_{ж ,} т.е. величиной V_ж можно пренебречь. Тогда уравнение Клапейрона–Клаузиуса запишется в виде:

Пар подчиняется законам идеального газа: PV=RT , тогда , преобразуем уравнение, переставляя давление Р в левую часть уравнения, а dT в правую часть. Получаем:

или

Проведем интегрирование уравнения (1) в пределах от Т₁ до Т₂ и соответственно от Р₁ до Р₂ при условии, что в области невысоких давлений пара ∆Н_исп ≈ const; в результате интегрирования получим:

∆Н_исп / R = const, выносим за знак интеграла

При помощи уравнения (2) можно графически определить значения теплоты испарения, если известны давления Р₁ и Р₂ и соответствующие им температуры испарения Т₁ и Т₂ . Для этого необходимо отложить на оси абсцисс значения обратной температуры, а на оси ординат – lnP.

Зависимость lnP от 1/Т будет линейной, а тангенс угла наклона этой прямой равен , т.е. , а

Расчетные значения ∆Н_исп получаются с достаточной для практики точностью, не уступающей точности непосредственного измерения. Возможно использование уравнения (2) для обратного расчета, когда по значению ∆Н_исп определяют изменение давления при изменении температуры в процессе испарения.

Теплоту фазовых переходов можно определить и по величине стандартной энтальпии образования, в зависимости от фазового состояния продуктов реакции.

Пример. Лучше всего это показать на примере теплоты образования воды из газообразных кислорода и водорода, которая составляет

для водяного пара ∆Н_(г) 0 = -241,82 кДж/моль; для воды в жидком состоянии ∆Н_(ж) 0 = -285,83 кДж/моль; для льда ∆Н_(тв) 0 = -291,82 кДж/моль. Теплота конденсации воды равна:

а теплота превращения воды в лед:

Как видно, тепловой эффект фазовых переходов значительно меньше теплоты образования веществ.

В результате фазовых переходов происходит изменение энтропии. Такие изменения в зависимости от температуры представим на рисунке.

Как известно, энтропия идеального кристалла при абсолютном нуле равна нулю. С ростом температуры атомы (ионы) флуктуировать относительно равновесного положения, число возможных способов их размещения растет, и энтропия увеличивается (ΔS>0). При достижении температуры плавления (точка А на рисунке) кристаллическая решетка разрушается скачкообразно (отрезок АБ), увеличивается термодинамическая вероятность системы W, а в соответствии с формулой S=k∙lnW (где k – постоянная Больцмана) энтропия при переходе от твердого в жидкое состояние растет. Более значительный скачок энтропии имеет место при переходе из жидкого состояния в газообразное (отрезок ВГ), когда ближний порядок расположения частиц друг относительно друга нарушается, и движение частиц становится хаотичным.

Пример. Оценим скачок энтропии на примере фазовых переходов воды:

когда известны стандартные абсолютные значения энтропии S_тв 0 =39,4; S_ж 0 =69,9; S_г 0 =188,7 Дж/(моль·К).

В соответствии с рисунком для воды

По известной энтальпии фазового перехода можно рассчитать изменение энтропии в соответствии с формулой

Пример.Вычислим изменение энтропии в процессе парообразования 1 моля этилхлорида при 12,3 0 С, когда теплота испарения ∆Н_исп =24,16 кДж/моль.

Молекулярная масса = 64,5 г/моль.

В заключение отмечу, что мы рассматривали лишь фазовые переходы I рода. При фазовых переходах I рода свойства веществ, выражаемые, например, через химический потенциал, первыми производными одной из характеристических функций, изменяются скачком при непрерывном изменении соответствующих параметров: температуры, давления, объема и энтропии. При этом выделяется или поглощается теплота перехода ∆Н_пер в соответствии с уравнением Клапейрона–Клаузиуса.

Кроме них, однако, существуют фазовые переходы II рода. Они не сопровождаются выделением или поглощением теплоты, для них уравнение Клапейрона–Клаузиуса теряет смысл. Эти переходы характеризуют изменения в системе, которые не определяются объемом и запасом энергии. В этом случае первые производные одной из характеристических функций непрерывны, а вторые производные (например, теплоемкость) изменяются скачком. К фазовым переходам II рода относятся переходы парамагнетика в ферромагнетик, диэлектрика в сегнетоэлектрик, а также процессы возникновения сверхтекучести, сверхпроводимости и др.

В настоящее время насчитывается около 400 твердых минералов, для которых наблюдаются фазовые переходы II рода: рутил, анатаз, алмаз и особенно кварц, который имеет семь модификаций, причем наряду с фазовыми переходами I рода наблюдаются фазовые переходы II рода. Так, при 573 0 С и переходе модификации кварца β α теплоемкость и коэффициент линейного расширения изменяются скачкообразно (I род), но при этом поглощается теплота 10,9 кДж/моль (II род).