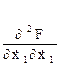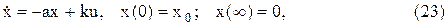Задачи на уравнение эйлера пуассона (2 видео)

Содержание

Уравнение Эйлера – Пуассона
Вариационное исчисление: примеры и задачи
Вариационное исчисление для чайников
Вариационное исчисление: задачи с решениями
Консультации и помощь
Интеграл Эйлера — Пуассона. Подробно о способах вычисления
📸 Видео

Видео:7.2 Задача 1. Краевая задача для уравнения ПуассонаСкачать

Уравнение Эйлера – Пуассона

Простейшую вариационную задачу можно обобщить на случай, когда подынтегральная функция содержит производные высших порядков и функционал имеет вид

. (1)

Здесь функция F предлагает (n+2) раза дифференцируемой по всем аргументам, а граничные условия заданы в форме

(2)

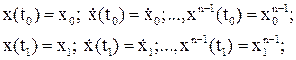
т.е. в граничных точках заданы значения не только функции, но и ее производных до порядка (n-1) включительно (всего 2n условий).

Решение задачи J = min ищется в классе C₂_n[t₀,t₁] гладких 2n раз дифференцируемых функций. Методика получения необходимого условия минимума функционала остается прежней: находится первая вариация критерия и приравнивается к нулю, что после преобразований приводит к уравнению

, (3)

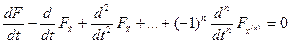
которые называются уравнением Эйлера-Пуассона и представляет в общем случае нелинейное дифференциальное уравнение 2n-порядка.

Его решение x(t,c₁,c₂,…,c₂_n) содержит 2n постоянных интегрирования. Последние находятся на основании такого же количества граничных условий (2).

Дадим вывод уравнения (3), ограничившись для простоты выкладок случаем, когда функционал зависит от производной не старше второго порядка:

. (4)

Предположим, что экстремум достигается на функции x(t), и прибавим к ней вариацию такую, что на концах при t=t₀ и t=t₁ как обращаются в нуль.

Определим вариацию функционала

. (5)

Преобразуем теперь выражение (5), пользуясь формулой интегрирования по частям, причем третий член вариации будем интегрировать по частям дважды:

(6)

. (7)

Вследствие условий на концах участка все неинтегральные члены обращаются в нуль, и, следовательно, на основе (5) — (7) получаем

. (8)

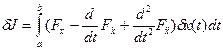
Поскольку необходимым условием экстремума является равенство нулю первой вариации функционала, а вариация произвольна, то из равенства и леммы Лагранжа (основной леммы вариационного исчисления) следует уравнение (3).

В этом случае имеет место следующий аналог условия Лагранжа, позволяющий отличить максимум от минимума функционала (1): если функция x(t) доставляет минимум (максимум) функционалу, необходимо, чтобы ).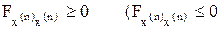

Пример. Применим теорему Лежандра к функционалу

Следовательно, функционал достигает минимума на функции x(t) = t 2 , которую мы определили ранее.

Проверим это. Для чего подставим экстремаль в функционал и вычислим его значение

Для сравнения вычислим значения функционала, например, на прямой линии, соединяющей те же точки (см. предыдущий рис.) – x(t) = t:

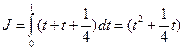
Таким образом, мы убедились, что на экстремали x(t) = t 2 значения функционала меньше, чем на кривой x(t) = t: , т.е. функционал действительно достигает на экстремали минимума, как это указывалось в условии Лежандра.

6. Задачи на условный экстремум: метод множителей Лагранжа.

Решение многих технических вопросов приводит к таким вариационным задачам, в которых функции, доставляющие экстремум должны, кроме того, удовлетворять некоторым дополнительным условиям. Так, например, в задаче о кратчайшей морской трассе на поверхности земного шара нужно найти минимум функционала – длины кривой

(1)

при условии, что эта кривая лежит на поверхности земного шара, т.е. удовлетворяет уравнению сферы . (2)

Экстремум функционала, определяемый при таком дополнительном условии называется условным экстремумом.

Наиболее простой в методическом плане способ решения указанной задачи на условный экстремум состоит в следующем. Из уравнения (2) выражаем функцию z(x) через функцию y(x)

и дифференцируем ее по х:

. (3)

Подставляем функцию (3) в функционал (1)

. (4)

Таким образом исходная задача на условный экстремум (1), (2) сведена к стандартной задаче на поиск экстремума функционала (4).

Однако необходимо подчеркнуть, что указанная процедура исключения неизвестных приводит часто к сложным вычислениям, а во многих случаях не может быть выполнена точно аналитически. В связи с этим Лагранжем был предложен другой достаточно простой метод решения – метод неопределенных множителей (множителей Лагранжа).

Сформулируем в общем виде задачу на условный экстремум.

Пусть задан функционал

(4)

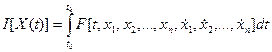
при наличии условий i=1,…,m, m

Функции i=1,…,m предполагаются гладкими и независимыми по переменным x₁,…,x_n .

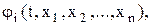
Теорема. Если X(t) – экстремаль функционала (4), удовлетворяющая условиям (5),(6), то она удовлетворяет уравнениям Эйлера, составленным для функционала

, (7)

где — соответствующим образом подобранные функции (множители Лагранжа).

В соответствии с данной теоремой, экстремали функционала (4) и функции , i=1,…,m должны удовлетворять уравнениям:

, (8)

(9)

так называемая функция Лагранжа.

Таким образом экстремаль задачи (4) — (6) определяется обычными методами поисками экстремалей функционала

Докажем справедливость теоремы на примере задачи при n=2, m=1:

(10)

(11)

Записываем функцию Лагранжа .

Для определения трех функций x(t), y(t), в соответствии с теоремой имеем как раз три уравнения Эйлера:

, (12)

Для доказательства теоремы получим соотношения (12) с использованием вариационных методов. Предположим, что экстремум функционала (10) доставляется функциями x(t) и y(t); добавим к ним вариации , отличные от нуля только в окрестности точки t = c, и обозначим

Отметим, что поскольку определяются не достаточные, а только необходимые условия экстремума, то вариации можно брать наиболее удобные для дальнейших выкладок, от этого общность вывода не снижается.

Вариация функционала (10) будет равна

(13)

Однако вариации в уравнении (13) не произвольны, а подчинены условию, требующему, чтобы проварьированные функции y+ , как и исходные, удовлетворяли уравнению связи (11), т.е.

. (14)

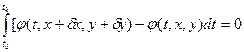
Используя понятие дифференциала функции многих переменных и теорему о значении определенного интеграла, соотношение (14) преобразуем к виду

. (15)

Подставляя равенство (15) в выражение для вариации (13), получаем

откуда вследствие вытекает, что выражение в квадратных скобках равно нулю, т.е.

. (16)

Обозначая правую и левую часть равенства (16) через , приходим как раз к уравнениям (12). Это доказывает теорему в случае n=2, m=1. При больших значениях n, m теорема доказывается аналогично.

7. Вариационные изопериметрические задачи. Особенности их решения.

Как частный случай задачи Лагранжа можно рассматривать и представляющую самостоятельный интерес изопериметрическую задачу, когда условия которым подчинена искомая функция, заданы в интегральной форме. Например, простейшая задача формулируется следующим образом: определить экстремум функционала

(22)

при условии, что другой функционал

(23)

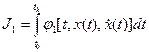
сохраняет заданное значение С, а экстремаль проходит через точки: x(t₀)=x₀; x(t_k)=x_k. Название изопериметрических такого рода задачи получили по названию одной из них: среди всех кривых равной длины (одинакового периметра) найти ту, которая ограничивает наибольшую площадь. Эта задача была известна еще древним грекам под названием «задача Дидоны». По преданию, легендарная основательница Карфагена царица Дидона покупала у туземцев землю, на которой должен быть основан город. Ей согласились продать лишь участок, который можно охватить бычьей шкурой. Тогда Дидона разрезала шкуру на тонкие ремни и расположила их так, чтобы охватить наибольшую площадь. Если пользоваться современными математическими понятиями, Дидона решила именно изопериметрическую задачу, выбирая функцию y(x), доставляющую максимум интегралу

(24)

(площади, охваченной ремнем), при заданном значении интеграла

(25)

Изопериметрическую задачу легко свести к общей задаче Лагранжа. Действительно, обозначив

(26)

(интеграл с переменным верхним пределом), получим

(27)

и приходим к следующей задаче Лагранжа: найти функции x(t), , доставляющие экстремум функционалу (22) при наличии уравнения связи .

Согласно теореме, для решения этой задачи следует составить уравнение Эйлера для вспомогательной функции (28) которые будут иметь вид

. (29)

Из второго уравнения (29) следует, что =const, т.е. для изопериметрической задачи множитель Лагранжа обращается в постоянное число. В тоже время это уравнение не дает никакой информации о функции , однако в этом и нет необходимости: ведь мы должны найти только одну функцию x(t), доставляющую экстремум функционалу (22) при наличии условия (23). Для этого достаточно одного уравнения – первого уравнения системы (29), в котором .

Таким образом, получаем следующее мнемоническое правило: для того чтобы найти функцию x(t), доставляющую экстремум интегралу (22) при условии, что интеграл (23) сохраняет заданное значение, следует составить одно уравнение Эйлера для промежуточной функции

. (30)

В решение уравнения Эйлера будут входить три произвольные постоянные – две постоянные интегрирования и постоянная 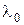. Для их определения имеем как раз три уравнения: два уравнения следуют из условий прохождения экстремали через две заданные точки, а третье – из условия, что интеграл (23) равен заданному значению С.

Применяя это правило к задаче Дидоны можно установить, что ее решение является окружностью с радиусом 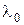[3]. Так при этом значение функционала равно С, то отсюда находим значение множителя Лагранжа .

8. Функционалы, зависимые от многих функций: уравнения Эйлера, условие Лежандра.

Одним из обобщений простейшей вариационной задачи является задача отыскания экстремума функционала, зависящего от n функций (9)

при заданных граничных значениях для всех функций

. (10)

Требуется в классе функций C₁[t₀,t₁] найти функции x_i(t), i=1,2,…,n, проходящие через граничные точки (10) и доставляющие минимум функционалу (9).

Для получения необходимых условий экстремума рассматриваемого функционала будем варьировать лишь одну из функций x_i(t), i=1,2,…n, оставляя все остальные функции неизменными. При этом функционал превращается в функционал, зависящий лишь от одной варьируемой функции, например, от x_j(t) = и следовательно, функция, реализующая экстремум, должна удовлетворять уравнению Эйлера

Так как это рассуждение применимо к любой функции x_j, j=1,2…,n ,то получаем систему дифференциальных уравнений Эйлера

, (11)

которая определяет совокупность необходимых условий экстремума вариационной задачи (9), (10).

Экстремали, соответствующие системе (11), содержат 2n постоянных интегрирования, находящихся из заданных граничных условий (10).

В современной литературе по теории оптимального управления полученный результат часто записывают в матричной форме. Введем в рассмотрение вектор 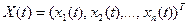и запишем функционалл (9) в следующем виде

Используя понятие производной скалярной функции от векторного аргумента Х

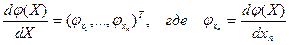
условия (11) можно записать в компактной матричной форме . (12)

(полный аналог скалярного уравнения Эйлера).

Используя матричные операции легко записать условия Лежандра для функционала (9). С этой целью введем в рассмотрение матрицу

, (13)

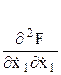
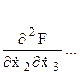
которая является аналогом скалярного выражения .

Для достижения на некоторой совокупности экстремалей минимума функционала (9) необходимо, чтобы все угловые миноры этой матрицы были неотрицательны, т.е.

, …, ,

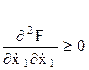
где символ определителя. В математике условия (14) известны как необходимые и достаточные условия Сильвестра положительной определенности матрицы Г.

Для достижения максимума J неравенства (14) должны иметь противоположный знак.

Функционал (9) может содержать производные высших порядков. В этом случае система уравнений будет состоять из уравнений Эйлера-Пуассона.

9. Применение классического вариационного исчисления к задаче оптимального управления, двухточечная краевая задача.

10. Применение классического вариационного исчисления к задаче оптимального управления, уравнения Эйлера — Лагранжа в канонической форме.

Вспомним теперь формулировку задачи оптимального управления с закрепленными концами. Объект управления описывается уравнениями

Требуется найти вектор управляющих воздействий u(t) и соответствующую фазовую траекторию x(t) при условии, что X(t₀) = X₀, X(t_k) = X_k и функционал

принимает экстремальное значение.

Очевидно, что сформулированная задача по существу является вариационной задачей и отличается от обычной вариационной задачи на условный экстремум только тем, что в нее входят два вида функций: функция X(t), характеризующая состояние системы, и функция управления U(t).Это отличие не принципиально и легко показать, что задача оптимального управления, удовлетворяющая основным положениям классического вариационного исчисления (отсутствие ограничений на фазовые координаты и управляющие воздействия, непрерывность и дифференцируемость управляющих воздействий), является общей задачей Лагранжа. Действительно, интеграл (9) можно рассматривать как функционал, зависящий от n+m функций x₁,…,x_n, u₁,…,u_n.

Эти функции связаны дифференциальными уравнениями объекта (8), которые можно записать в виде уравнений связи

. (10)

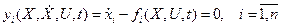
Следовательно, для решения задачи оптимального управления, которая удовлетворяет основным положениям классического вариационного исчисления, можно использовать метод неопределенных множителей Лагранжа и записать необходимое условие экстремума функционала (9) при наличии ограничения (10) в виде уравнения Эйлера – Лагранжа. Согласно методу неопределенных множителей введем вспомогательный функционал

(11)

(12)

есть функция Лагранжа. Тогда уравнение Эйлера-Лагранжа будут иметь вид

(13)

В дальнейшем будем использовать, так называемую каноническую форму записи уравнений Эйлера-Лагранжа. Такая форма записи уравнения Эйлера-Лагранжа имеется в вариационном исчислении мы рассмотрим ее применительно к задачам оптимального управления.

Введем функцию, называемую гамильтонианом (функция Гамильтона).

(14)

(l₀=-1) и сравним ее с функцией Лагранжа (12). Выразим вспомогательную функцию L через гамильтониан H:

(15)

(т.е. к функции H добавлено слагаемое, которое отличает ее от функции L).

Запишем необходимое условие экстремума (уравнения Эйлера-Лагранжа) с использованием функции H. Для частных производных, которые входят в уравнения Эйлера-Лагранжа (13) согласно (15) имеем

(16)

Подставим найденные выражения в (13), получим уравнения Эйлера-Лагранжа в канонической форме:

Здесь уравнения (17а) являются уравнениями объекта (8). Уравнения (17б), записанные относительно вспомогательных переменных , образуют так называемую сопряженную к (17а) систему. Они согласно (14) имеют вид :

Уравнения (17в) являются алгебраическими. Действительно

Заметим, что значения функции, удовлетворяющие условию в виде (17в), называются стационарными значениями функции, а точки пространства аргументов, в которых эти условия выполняются — стационарными точками (стационарными называются точки, в которых производная функции равна нулю). Следовательно, оптимальное управление есть стационарная точка функции Гамильтона.

Уравнения (19) позволяют определить управление в виде функции

. (20)

Подставив (20) в (17а и б), получим систему дифференциальных уравнений:

(21)

Общее решение такой системы, как известно, зависит от 2n параметров (начальных условий) поскольку управление найдено как функция (X и l). В задаче с закрепленными концами n параметров задано на левом конце фазовой траектории (X(t₀)=X₀), и n параметров на правом конце (X(t_k)=X_k). Такая задача называется краевой.

Таким образом решение задачи оптимального управления оказалось сведенным к решению краевой задачи для систем дифференциальных уравнений. Отметим, что в силу только необходимости уравнений Эйлера-Лагранжа решения системы (17) не обязательно дают оптимальное управление, но только решение системы (17) могут претендовать на роль оптимального управления. С помощью уравнений Эйлера-Лагранжа обычно удается найти оптимальное управление и оптимальную траекторию системы, поскольку существование и характер экстремума функционала в конкретной задаче оптимального управления, как правило, известно заранее.

Пример. Определим из условия минимума функционала

(22)

оптимальное управление U(t) для объекта, описываемого уравнениями

составим функцию Гамильтона

. (24)

Уравнение Эйлера-Лагранжа имеет вид

(25)

Из последнего уравнения имеем (26)

Исключим из оставшихся двух уравнений l. Для чего подставим уравнение (26) в первое уравнение (25)

откуда

Затем продифференцируем

После чего подставим во второе уравнение (25)

Окончательно имеем уравнение относительно x(t):

(27)

Решением этого уравнения является функция

(28)

Постоянные С₁ и С₂ определяются из граничных условий. Так как x(¥)=0, то

(29)

и для выполнения (29) необходимо положить С₁=0.

При t=0 имеем x(0)=x₀, тогда

(30)

и для выполнения равенства (30) должно быть С₂ = x₀, следовательно

. (31)

Используя уравнение (23) – уравнение объекта, найдем

. (32)

Управление (32) найдено как функция времени и начальных условий – это так называемое программное управление.

В данном примере легко найти и управление в форме обратной связи. Из сравнений выражений (31) и (32) следует

(33)

Видео:Интеграл Эйлера-Пуассона: e^(-x^2)Скачать

Вариационное исчисление: примеры и задачи

Видео:Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Вариационное исчисление для чайников

Древнейшей из задач на максимум и минимум является задача отыскания среди плоских замкнутных кривых заданной длины такую, которая охватывает наибольшую площадь (5 в до н.э.) — и это классическая изопериметрическая задача вариационного исчисления. Началось же классическое вариационное исчисление с задачи о кривой наискорейшего спуска (брахистохроне) в 1696 г. с публикации Иоганна Бернулли.

Общие принципы и методы решения задач вариационного исчисления были введены в 18 веке Эйлером и Лангранжем, они же установили тесную связь между ВИ и естествознанием. Далее на протяжении более чем двух столетий они разрабатывались, были найдены помимо необходимых условий первого порядка (уравнений Эйлера-Лагранжа) необходимые и достаточные услвоия второго порядка для сильных и слабых экстремумов.

На этой странице мы рассмотрим примеры с подробным решением следующих типов: простейшая задача вариационного исчисления, задача Больца, изопериметрическая задача, задача со старшими производными. А также научимся находить вариацию и допустимые экстремали функционала. Все это относится к классическому вариационному исчислению.

Видео:Найти экстремаль функционалаСкачать

Вариационное исчисление: задачи с решениями

Задача 1. Решить классическую задачу вариационного исчисления:

$$ int_0^1 dot^2 dt to extr, quad x(0)=1, x(1)=0. $$

Задача 2. Решить задачу Больца

$$ int_0^1 dot^2 dt +alpha x^2(1) to extr, quad x(0)=1. $$

Задача 3. Решить изопериметрическую задачу

$$ int_0^1 dot^2 dt to extr, int_0^1 x^2 dt =3, quad x(0)=1, x(1)=6. $$

Задача 4. Решить задачу со старшими производными

$$ int_0^pi (ddot^2+4x^2) dt to extr, quad x(0) = dot x(0)=0, , dot x(pi)=sh(pi). $$

Задача 5. Найти все экстремали функционала $J(y)$, удовлетворяющие указанным граничным условиям

$$ J(y)=int_0^1 (e^y +xy’)dx, quad y(0)=0, y(1)=1. $$

Задача 6. Найти все экстремали функционала $J(y)$, удовлетворяющие указанным граничным условиям

$$ J(y)=int_0^1 e^cdot y» ^2 dx, quad y(0)=0, y'(0)=1, y(1)=e, y'(1)=2e. $$

Задача 7. Для указанной вариационной задачи записать уравнение Эйлера и найти экстремаль, удовлетворяющую условиям $y(0) = 19, y(1)=30$

Задача 8. Найти вариацию функционала

$$int_0^1 (x+y’)ln sin y’ dx.$$

Задача 9. Найти все экстремали функционала $J(y)$, удовлетворяющие указанным граничным условиям

$$ J(y)=int_0^ (4ysin x +y’^2-y^2)dx, quad y(0)=0, y(pi/4)=0. $$

Видео:Интеграл ПуассонаСкачать

Консультации и помощь

Нужно выполнить контрольную работу или задачи по вариационному исчислению и смежным предметам? Нет проблем! Стоимость консультации по решению — от 150 рублей, подробное оформление согласно требованиям методички в Word.

Видео:7.6 Задача 5. Краевая задача для уравнения ПуассонаСкачать

Интеграл Эйлера — Пуассона. Подробно о способах вычисления

В статье подробно, вплоть до самых мелочей, рассмотрены три способа взятия интеграла Эйлера-Пуассона. В одном из способов выводится вспомогательная формула редукции. Для нахождения некоторых сложных интегралов можно использовать формулы редукции, которые позволяют понизить степень подынтегрального выражения и вычислить соответствующие интегралы за конечное число шагов.

Данный интеграл берется от гауссовой функции:
Здесь есть очень интересный математический способ. Чтобы найти исходный интеграл, сначала ищут квадрат этого интеграла, а потом от результата берут корень. Почему? Да потому что так гораздо проще и безболезненно можно перейти в полярный координаты. Поэтому, рассмотрим квадрат Гауссового интеграла:

Мы видим, что у нас получается двойной интеграл от некоторой функции . В конце этого поверхностного интеграла стоит элемент площади в декартовой системе координат .
Теперь давайте переходить в полярную систему координат:

Тут нужно заметить, что r может изменяться в пределах от 0 до +∞, т.к. x изменялось в таких же пределах. А вот угол φ изменяется от 0 до π/2, что описывают область интегрирования в первой четверти декартовой системы координат. Подставляя в исходный, получим:

В силу симметричности интеграла и положительной области значений подынтегральной функции, можно заключить, что

Давайте поищем ещё какие-нибудь решения? Это ведь интересно! 🙂

Рассмотрим функцию
А теперь вспомним школьную математику и проведем простейшее исследование функции с помощью производных и пределов. Не то, чтобы мы здесь будем считать сложные пределы (ведь в школе их не проходят), а просто порассуждаем что будет с функцией, если её аргумент стремится к нулю или к бесконечности, таким образом прикинем асимптотическое поведение, что в математике всегда очень важно. Это похоже на качественную оценку того, что происходит.

0 to gleft( t right) — <rm> \ t > 0 to — te^

Она ограничена сверху единицей на интервале (-∞;+∞) и нулем на интервале [-1;+∞).

Cделаем следующую замену переменных
И получим:

Ограничим в первом неравенстве изменение (0,1), а во втором — промежутком (0;+∞), возведём оба неравенства в степень n, так как неравенства с положительными членами можно возводить в любую положительную степень. Получим:

1 \ end right.> \ end $» data-tex=»display»/>

Давайте для наглядного доказательства неравенств построим графики при n = 1

Теперь попробуем проинтегрировать неравенства в пределах, которые указаны в соответствующих системах. И сразу объединим всё в одно неравенство:

Опять таки, если посмотреть на графики, то данное неравенство справедливо.

С учетом небольшой замены, легко увидеть, что:

Т.е. в том большом неравенстве в середине у нас интеграл Эйлера-Пуассона, а вот теперь нам нужно найти интегралы, которые стоят на границах данного неравенства.

Найдем интеграл от левой границы:

Для того, чтобы его посчитать и оценить, давайте сначала найдем интеграл общего вида. Сейчас я покажу вам как можно вывести формулу редукции ( в математике под такими формулами подразумевают понижения степени ) для данного интеграла.

Теперь если с помощью формулы редукции рассмотреть тот же интеграл, но с нашими пределами от 0 до π/2, то можно сделать некоторые упрощения:

Как мы видим, понижать можно до бесконечности (зависит от n). Однако, и тут есть одна тонкость. Формула изменяется в зависимости то того, является ли n четным числом или не является.
Для этого рассмотрим два случая.

Где n!! — двойной факториал. Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1, n], имеющих ту же чётность что и n

В силу того, что 2n+1 — нечетное число при любом значении n, получим для левой границы нашего неравенства:

Найдем интеграл от правой границы:
(здесь используем ту же формулу редукции, которую доказали ранее)

После того, как мы оценили левую и правую части неравенства, сделаем некоторые преобразования, чтобы оценить пределы левой и правой частей неравенства при условии, что n стремится к ∞:

Возведем обе части неравенства в квадрат:

Теперь сделаем небольшое лирическое отступление. В 1655 году Джон Валлис (английский математик, один из предшественников математического анализа.) предложил формулу для определения числа π. Дж. Валлис пришёл к ней, вычисляя площадь круга. Это произведение сходится крайне медленно, поэтому для практического вычисления числа π формула Валлиса мало пригодна. Но для оценки нашего выражения она отлично подходит 🙂

Теперь преобразуем наше неравенство так, чтобы мы могли увидеть где подставить формулу Валлиса:

Из формулы Валлиса следует, что и левое, и правое выражение стремятся к π/4 при n → ∞
В силу того, что функция exp[-x²] является четной, мы смело полагаем, что

Впервые одномерный гауссов интеграл вычислен в 1729 году Эйлером, затем Пуассон нашел простой приём его вычисления. В связи с этим он получил название интеграла Эйлера — Пуассона.

Давайте еще попробуем вычислить Гауссов интеграл. Его можно написать в разных видах. Ведь ничего не меняет изменение название переменной, по которой идет интегрирование.