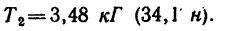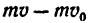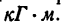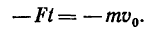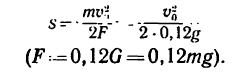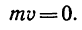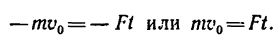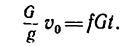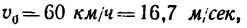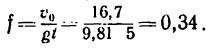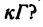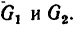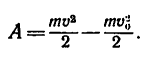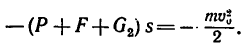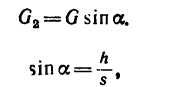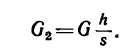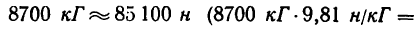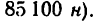Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать

Решение задач на тему «динамика поступательного движения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Тема: Динамика поступательного движения.

Контрольные вопросы для подготовки к занятию

1. В чём заключается основная задача динамики?

2. Что называется инерциальными системами отсчёта?

3. Что понимается под массой? Ед. измерения в СИ?

4. Дайте определение силы и поясните основные признаки и свойства силы.

5. Сформулируйте и объясните 1 закон Ньютона.

6. Сформулируйте и объясните 2 закон Ньютона. Запишите основное равнение динамики.

7. Что называется импульсом тела? Единица измерения?

8. Что называется импульсом силы? Единица измерения?

9. Закон сохранения импульса.

10. Перечислите механические силы. Как каждая из них направлена? Напишите формулы, по которым они определяются? (Сила тяготения, сила тяжести, вес тела, сила упругости, сила трения).

11. Сформулируйте и объясните 3 закон Ньютона.

Краткие теоретические сведения и основные формулы

1. Динамика – раздел механики, изучающий движение материальных тел под действием приложенных к ним сил.

2. ИСО – это система отсчёта, в которой справедлив закон инерции. Всякая система отсчёта, движущаяся по отношению к ИСО поступательно, равномерно и прямолинейно, есть также ИСО. Следовательно, теоретически может существовать любое число равноправных ИСО, обладающих тем важным свойством, что во всех таких системах законы физики одинаковы (принцип относительности).

3. Масса – физическая величина, одна из основных характеристик материи, определяющих её инерционные и гравитационные свойства.

4. Сила – физическая векторная величина, являющаяся количественной мерой механического взаимодействия материальных объектов.

Во II законе Ньютона масса выступает как мера инертности тел.

Признак и силы: 1) числовое значение (величина); 2) направление; 3) точка приложения.

Свойства силы: 1. Точка приложения силы может быть перенесена по линии действия силы.

2. Если к данному телу одновременно приложено несколько

сил, то каждая из них действует так, как если бы других сил не было.

5. I закон Ньютона : материальная точка сохраняет состояние покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит её изменить это состояние.

6. II закон Ньютона: ускорение, приобретаемое телом, совпадает по направлению с действующей на него силой и равно отношению этой силы к массе тела:

где — равнодействующая всех сил, приложенных к телу; определяется по правилу сложения векторов.

Чем больше масса тела, тем большую силу к нему нужно приложить для сообщения определённого ускорения.

II закон Ньютона в классической физике ( m = const ) может быть записан в виде:

В общем случае при переменной массе II закон Ньютона выражается формулой:

7. Импульс тела: – физическая векторная величина, равная произведению массы тела на его скорость и имеющая направление скорости.

8. Импульс силы

Импульс силы – физическая векторная величина, равная произведению силы и времени её действия.

Импульс силы, действующий на тело, равен изменению импульса тела.

В случае действия постоянной силы

где и — начальная и конечная скорости, разделённые промежутком D t .

В случае прямолинейного равнопеременного движения

9. Закон сохранения импульса: .

10. Сила возникает как при непосредственном контакте (давление прижатых друг другу тел, трения), так и через посредство создаваемых телами полей (поле тяготения, электромагнитное поле).

1) Все тела притягиваются друг к другу. Для материальной точки (или шаров) закон всемирного тяготения имеет вид:

где и – массы тел, r – расстояние между материальными точками или центрами шаров; G – гравитационная постоянная.

Если тело массой m находится над поверхностью Земли на высоте h , то на него действует сила тяготения

где М — масса Земли, R = 6,37 . 10 6 м – радиус Земли.

2) Сила тяжести F _тяж определяется силой притяжения Земли и тем, что Земля вращается вокруг собственной оси. В связи с малостью угловой скорости вращения Земли ( w = 7,27 . 10 -5 ) сила тяжести мало отличается от силы тяготения.

При h R ускорение, создаваемое силой тяжести является ускорением свободного падения g = G .

3) Вес – сила, с которой тело вследствие тяготения к Земле действует на опору (или подвес), удерживающую тело от свободного падения.

Вес тела проявляется в том случае, если тело движется с ускорением, отличным от g , то есть когда на тело, кроме силы тяжести действуют другие силы. Эта сила приложена либо к опоре, либо к подвесу.

Вес тела равен силе тяжести только в том случае, когда ускорение тела относительно Земли равно нулю, т.е., когда тело относительно Земли неподвижно или движется с постоянной скоростью.

4) Сила, вызванная деформацией тел и препятствующая изменению объёма или формы тела, называется силой упругости.

При небольших деформациях растяжения или сжатие x сила упругости прямо пропорциональна деформации и направлена в сторону, противоположную ей (закон Гука):

где k – коэффициент упругости, зависит от свойств материала и геометрии деформируемого тела.

Закон Гука может быть записан в виде:

где e = — относительная деформация; — длина тела до деформации (начальная длина); — длина тела после деформации; s = — напряжение, возникающее в твердом теле, S – площадь сечения, на которую действует сила F ; E – модуль Юнга.

5) Сила трения – сила сопротивления, направленная противоположно относительному перемещению данного тела и приложенная по касательной к соприкасающимся поверхностям:

где m — коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей; N – сила нормального давления.

11. III закон Ньютона: материальные точки действуют друг на друга с силами, численно равными по величине, и направленными в противоположные стороны вдоль прямой, соединяющей эти точки. .

Методика решения задач

1. Сделать схематический чертеж согласно условию задачи.

2. Проставить вектор ускорения.

3. Расставить все силы, приложенные к телу со стороны других тел.

4. Составить основное уравнение динамики поступательного движения

в векторной форме.

5. Выбрать систему координат для каждого тела отдельно. Начало координат совместить с центром масс тел.

6. Найти проекции всех сил на оси координат.

7. Записать основное уравнение динамики в проекциях на оси координат . При этом необходимо следить за знаками проекций векторов сил. Если направление проекции вектора совпадает с положительным направлением координатной оси, то проекция силы берется со знаком (+), если не совпадает – со знаком (-).

8. Решить систему полученных уравнений относительно неизвестной величины.

Примеры решения задач

Задача 1. Поезд весом 5 МН после прекращения тяги паровоза под действием силы трения 100 кН останавливается через 1 мин. С какой скоростью шел поезд?

Дано: Р = 5∙10 6 Н; F _тр = 100∙10 3 Н; t = 60 c ; = 0; F = 0.

Найти: .

1. ; (1)

2. Приложим к центру масс силы, действующие на тело.

3. Составим уравнение движения (запишем II закон Ньютона) в векторном виде:

.

4. Выберем систему координат для решения векторного уравнения.

5. Найдем проекции всех сил на оси координат.

х : (2);

у :

6) Из (2) найдем ускорение а : ;

7) Массу найдем из m = P / g — подставим в « а »:

— подставим в (1): .

Задача 2. Определить силу трения, действующую при движении тела по горизонтальной поверхности, если на тело массой m = 1 кг действует сила 10 Н под углом a = 60 ° к горизонту. Коэффициент трения равен m = 0,1. С каким ускорением будет двигаться тело (рис.2.3)?

Дано:

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

m = 0,1

F _тр — ? — ?

Решение

1. Приложим к центру масс силы, действующие на тело.

2. Составим уравнение движения (запишем II закон Ньютона) в векторном виде:

.

3. Выберем систему координат для решения векторного уравнения.

4. Найдем проекции всех сил на оси координат.

Ось X : ; ; ; .

Ось Y : ; ; .

5. Составим систему уравнений для решения векторного уравнения.

;

; .

; ( .)

Ответ: Н; .

Задача 3. Найти ускорение тела, соскальзывающего с наклонной плоскости, образующей с горизонтом угол = 30 0 . Коэффициент трения между телом и плоскостью = 0,3.

Дано: = 30 0 ; = 0,3.

Движение тела вниз по наклонной плоскости с ускорением а , направленным вниз по плоскости, может происходить, если скатывающая сила F превышает силу трения F _тр ( F > F _тр ), а их разность вызывает ускорение, направленное вниз вдоль наклонной плоскости.

По 2 закону Ньютона: .

В проекциях на оси х и у :

х : .

y : .

, подставим в « а »

2,4 м/с 2 .

Ответ: а = 2,4 м/с 2 .

Задача 4. Две гири массами и висят на концах нити, перекинутой через блок. Первая гиря находится на 2 м ниже второй. Гири пришли в движение без начальной скорости. Через какое время они будут находиться на одной высоте?

Дано: ; ; h = 2 м ; = 0. Найти: t .

; ; ;

1) ; проекция на ось y :

2) проекция на ось y :

, подставим в t :

.

Задача 5. Стальной трос торпедно-погрузочного аппарата подводной лодки выдерживает на разрыв нагрузку 25 кН. С каким наибольшим ускорением можно поднимать торпеду массой 1300 кг, подвешенную на этом тросе, чтобы он не разорвался?

На торпедно-погрузочный аппарат действует 2 силы: сила тяжести mg и сила натяжения троса F _н .

Наибольшее ускорение должно соответствовать величине силы натяжения троса F _н не больше или равной 25 кН.

По 2 закону Ньютона составим уравнение в векторной форме (см. рис.):

.

Найдем проекции этих сил на ось у: , отсюда найдем ускорение:

.

Ответ: а = 9,2 м/с 2 .

Задача 6. Найти абсолютное удлинение буксирного троса с жесткостью k = 100 кН при буксировке автомобиля массой 2 т с ускорением а = 0,5 м/с 2 .

k = 100∙10 3 Н Согласно закону Гука F _упр = — kx .

m = 2∙10 3 кг Сила натяжения, деформирующая трос, по 3 закону Ньютона

а = 0,5 м/с 2 численно равна силе упругости, но противоположна

_____________ ей по направлению. Поэтому

На буксируемый автомобиль действуют три силы: сила тяжести , сила реакции опоры и сила натяжения троса . По 2 закону Ньютона в векторном виде

,

а в скалярном виде . (1)

(т.к. по 3 закону Ньютона mg = N и в проекциях на ось у : mg – N = 0) .

Тогда .

Из (1) выразим х : = 0,01 м.

Задача 7. Каким должен быть радиус кривизны моста, чтобы автомобиль, движущейся со скоростью 19,6 м/с, оказался в невесомости на его середине?

= 19,6 м/с

— ?

; Найдем проекции сил на ось у.

у: , т.к. N = 0, ,

то ; м.

Видео:1 4 Динамика поступательного движенияСкачать

Задачи на поступательное движение тела в теоретической механике

Задачи на поступательное движение тела:

Если точка массой m, находясь под действием постоянной силы Р в течение t сек, двигается прямолинейно, то теорема об изменении количества движения выражается формулой

где разность

В СИ количество движения и импульс силы измеряются в ньютон-секундах (н-сек); в системе МКГСС— соответственно в килограмм-секундах в (кГ сек).

Если, рассматривая действие силы Р на материальную точку массой т, учитывать не продолжительность ее действия, а протяженность, т. е. то расстояние, на котором действует сила, то получим теорему об изменении кинетической энергии точки:

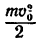
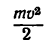
где А — работа всех сил, приложенных к точке, а и

кинетическая энергия точки соответственно в начале и

конце действия сил.

Кинетическая энергия измеряется единицами работы, т. е. в СИ — в джоулях (дж), в системе МКГСС—в

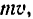
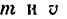
Необходимость введения двух динамических характеристик объясняется тем, что одна характеристика не отражает все особенности движения точки. Например, зная количество движения автомобиля (т. е. величину а не величины отдельности) и действующую на него при торможении силу, можно определить, через сколько секунд автомобиль остановится, но по этим данным нельзя найти пройденный за время торможения путь. Наоборот, зная начальную кинетическую энергию автомобиля и тормозящую силу, можно определить тормозной путь, но по этим данным нельзя найти время торможения.

Если же в задаче заданы и масса точки, и ее скорость, то в принципе можно использовать для решения любую из теорем, но при этом необходимо иметь в виду, что для определения времени движения целесообразно использовать теорему об изменении количества движения, а для определения пройденного пути — теорему об изменении кинетической энергии.

Уравнения (1) и (2) применимы также и при рассмотрении поступательно движущихся тел. В этом случае любое твердое тело отождествляется с материальной точкой, имеющей массу всего тела и расположенной в его центре массы или в точке, совпадающей с центром тяжести тела.

Задача №1

Машинист тепловоза отключает двигатель и начинает тормозить в момент, когда тепловоз имеет скорость 90 км/ч. Через сколько времени и пройдя какой путь тепловоз остановится, если сила торможения постоянна н составляет 0,12 его веса, а движение происходит по горизонтальному и прямолинейному участку дороги?

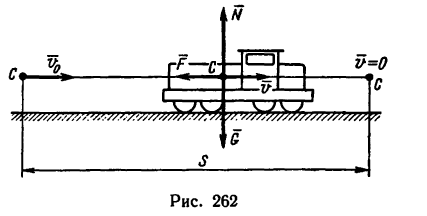
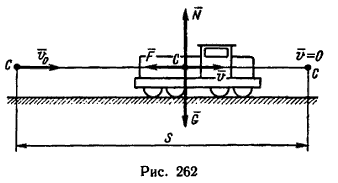
1. Тепловоз движется поступательно, поэтому рассмотрим движение его центра тяжести С (центра массы), считая, что к нему приложены все внешние силы (рис. 262).

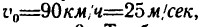
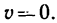
2. После того как отключается двигатель и включается тормозное устройство, на тепловоз действуют три силы: сила тяжести G, нормальная реакция рельсов Лг и сила торможения F. В начале торможения скорость в конце Требуется определить путь s и время t, за которое этот путь пройден (см. рис. 262).

3. Для определения времени торможения применим теорему об изменении количества движения.

Спроектировав векторы на горизонтальную ось

(ось х), увидим, что проекции сил G и N равны нулю, а проекция силы F получается равной ее модулю, но со знаком минус; проекция скорости 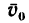также равна ее модулю, поэтому уравнение (1) в данном случае примет вид

4. Решаем это уравнение относительно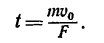
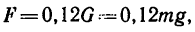
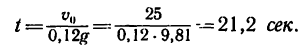
Так как сила торможения то окончательно

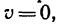
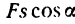
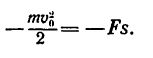
5. Для определения тормозного пути s применим теорему об изменении кинетической энергии. В данном случае А =(угол а между направлением силы F и направлением перемещения равен 180° и, следовательно, cos 0 = cos 180° = — 1, а работы сил G и N равны нулю (эти силы действуют перпендикулярно к направлению перемещения) поэтому уравнение (2) принимает вид

6. Решаем это уравнение относительно s:

После подстановки в эту формулу числовых значений

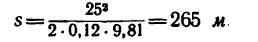
Таким образом, тепловоз остановится через 21,2 сек, пройдя 265 м.

Задача №2

Каков коэффициент трения колес заторможенного автомобиля о дорогу (считать, что заторможены все четыре колеса), если в момент выключения двигателя и нажатия тормоза скорость движения автомобиля 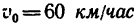и автомобиль останавливается через 5 сек после начала торможения.

1. В задаче известно время движения заторможенного автомобиля, т. е. имеется в виду импульс силы, поэтому для ее решения применим формулу (1)—закон количества движения.

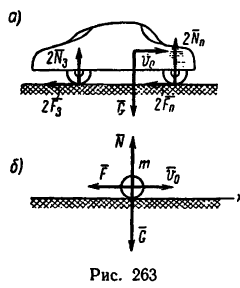
2. На заторможенный автомобиль действуют девять сил (рис. 263, а): С —вес автомобиля, четыре реакции поверхности дороги, приложенные к каждому колесу, и четыре силы трения, также приложенные к колесам.

Принимая автомобиль за материальную точку, считаем, что все эти силы приложены в центре тяжести автомобиля, и тогда, заменив четыре реакции поверхности их суммой R и четыре силы трения их суммой F, получим только три силы G, N и F(pnc. 263, б).

3. Силы G и N численно равны друг другу и взаимно уравновешиваются. Следовательно, импульс создается силой трения F.

4. Импульс силы трения в данном случае действует в сторону, противоположную движению, поэтому уравнение (1) для данной задачи примет вид

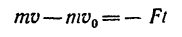
Но автомобиль через t = 5 сек останавливается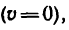, поэтому

5. Подставим сюда значения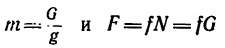(так как N = G):

Откуда, имея в виду, что

Эту задачу можно решить, используя теорему об изменении кинетической энергии. Рекомендуем этот вариант решения выполнить самостоятельно.

Задача №3

За 500 м до станции, стоящей на пригорке высотой 2 м, машинист поезда, идущего со скоростью 12 м/сек, закрывает пар и начинает тормозить Как велико должно быть сопротивление от торможения, считаемое постоянным, чтобы поезд остановился у станции, если масса поезда равна 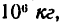сопротивление трения 2000

1. Решаем задачу, используя теорему об изменении кинетической энергии, так как в условии задачи задано уже не время торможения, а тормозной путь s = 500 м.

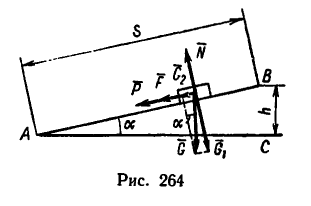
2. Поезд двигается поступательно, поэтому достаточно рассмотреть движение его центра тяжecYи О. Приложим к точке О все действующие силы (рис. 264). Вес поезда G разлагаем на две составляющие

На поезд в сторону, противоположную его движению, действуют три силы: составляющая веса 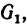сила трения F и искомая сила торможения Р.

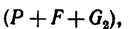
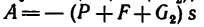
3. Равнодействующая этих сил, равная их сумме действуя на расстоянии s, производит работу (работа сил сопротивления отрицательна).

4. Работа А равна изменению кинетической энергии поезда [уравнение (2)]:

Но так как конечная скорость поезда 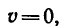то

Из последнего уравнения можно найти силу торможения Р:
5. Но предварительно нужно определить составляющую веса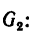
А так как

то

Затем вычисляем величину силы Р в системе МКГСС, учитывая, что

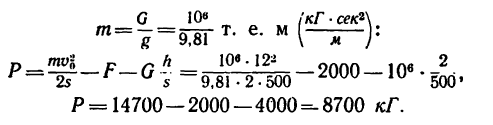
6. Если решить задачу в единицах СИ, то все предварительные рассуждения не изменятся, но в окончательную расчетную формулу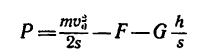

нужно подставить числовое значение силы F в ньютонах (F = = 2000 кГ = 19600 я), а вес G выразить через массу (G—mg):

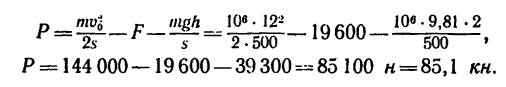
Легко заметить, что

• Задачи на вращательное движение тела
• Равновесие тяжелой рамы
• Расчет составной конструкции
• Момент силы относительно оси
• Равнопеременное вращательное движение
• Неравномерное вращательное движение
• Плоскопараллельное движение тела
• Определение передаточных отношений различных передач

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Задачи на поступательное движение тела

Видео:Динамика поступательного движения. Алгоритм решения задач.Скачать

Условие задачи

Машинист тепловоза отключает двигатель и начинает тормозить в момент, когда тепловоз имеет скорость 90 км/ч. Через сколько времени и пройдя какой путь тепловоз остановится, если сила торможения постоянна и составляет 0,12 его веса, а движение происходит по горизонтальному и прямолинейному участку дороги?

Видео:Поступательное и вращательное движенияСкачать

Решение задачи

1. Тепловоз движется поступательно, поэтому рассмотрим движение его центра тяжести C (центра массы), считая, что к нему приложены все внешние силы (рис. 262).

2. После того как отключается двигатель и включается тормозное устройство, на тепловоз действуют три силы: сила тяжести G, нормальная реакция рельсов N и сила торможения F. В начале торможения скорость v₀=90 км/ч=25 м/сек, а в конце v=0. Требуется определить путь s и время t, за которое этот путь пройден (см. рис. 262).

3. Для определения времени торможения применим теорему об изменении количества движения.

Спроектировав векторы на горизонтальную ось (ось x), увидим, что проекции сил G и N равны нулю, а проекция силы F получается равной ее модулю, но со знаком минус. Проекция скорости v₀ также равна ее модулю, поэтому уравнение (1) в данном случае примет вид
-Ft = -mv₀.

4. Решаем это уравнение относительно t:
t = mv₀/F.

Так как сила торможения F=0,12G=0,12mg, то окончательно
t = v₀/(0,12g) = 25/(0,12*9,81) = 21,2 сек.

5. Для определения тормозного пути s применим теорему об изменении кинетической энергии. В данном случае v=0, A=Fs cos α (угол α между направлением силы F и направлением перемещения равен 180° и, следовательно, cos 0=cos 180°=-1, а работы сил G и N равны нулю (эти силы действуют перпендикулярно к направлению перемещения), поэтому уравнение (2) принимает вид
-mv₀ 2 /2 = -Fs.

6. Решаем это уравнение относительно s:
s = mv₀ 2 /(2F) = v₀ 2 /(2*0,12g),
т.к. F = 0,12G = 0,12mg.

После подстановки в эту формулу числовых значений
s = 25 2 /(2*0,12*9,81) = 265 м.

Таким образом, тепловоз остановится через 21,2 сек, пройдя 265 м.

🔥 Видео

Динамика поступательного движения (реал). Решение задачи методом разделенных переменных.Скачать

Физика. Решение задач. Динамика поступательного движения.Скачать

Общее уравнение динамики. Задача 1Скачать

Кинематика поступательного и вращательного движения материальной точкиСкачать

7.2 Применение основного уравнения динамики вращательного движения. Школьная задача.Скачать

Урок 89 (осн). Задачи на вращательное движение - 1Скачать

Урок 57. Решение задач динамикиСкачать

Поступательное и вращательное движения.Скачать

Урок 56. Алгоритм решения задач динамикиСкачать

Динамика для ОГЭ и ЕГЭ по физикеСкачать

Методика решения задач по динамике материальной точки. Часть 1Скачать

Первая основная задача динамики. Задачи 1, 2, 3, 4Скачать

Динамика поступательного и вращательного движения. Коржуев А. В.Скачать