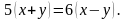Данная разработка предназначена для учеников 7 класса, а также для тех, кто желает отработать навык решения задач. Теоретическая часть содержит примеры решения задач с использованием систем уравнений. В практической части представлено большое количество задач с тематическим разделением.
- Просмотр содержимого документа «Решение задач с использованием систем линейных уравнений с двумя переменными.»
- Решение задач с помощью систем линейных уравнений
- Алгоритм решения задачи с помощью системы линейных уравнений
- Примеры
- Авторский учебный задачник «Решение систем линейных уравнений с двумя переменными»
- 🎬 Видео
Просмотр содержимого документа
«Решение задач с использованием систем линейных уравнений с двумя переменными.»
Решение задач с использованием систем линейных уравнений с двумя переменными.
Переходим теперь к практическому применению систем линейных уравнений с двумя переменными. Часто бывает, что в задачах неизвестны два, а то и три-четыре компонента. И в этом случае обозначение какого-то одного компонента переменной не облегчает решение задачи. Тогда нужно ввести две или три переменные. Вот здесь нам как раз и понадобится система уравнений и способы её решения. Приведём пример с полным описанием.
Например, решить задачу. Лодка за 3 ч движения по течению и 4 ч против течения проходит 114 км. Найдите скорость лодки по течению и её скорость против течения, если за 6 ч движения против течения она проходит такой же путь, как за 5 ч по течению.
Решение. В задаче описывается движение по воде. А значит, должна быть собственная скорость лодки и скорость течения реки. Они нам и не известны, поэтому обозначим через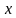 
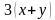
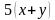
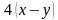
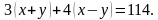
км/ч собственную скорость лодки, а через 
км/ч – скорость течения реки. Тогда скорость лодки по течению реки равна 
км/ч, а скорость лодки против течения реки — 
км/ч. За 3 ч движения по течению реки лодка пройдёт 
км, а за 5 ч — 
км. За 4 ч против течения лодка пройдёт 
км, а за 6 ч — 
км. По условию задачи известно, что за 3 ч по течению и 4 ч против течения лодка пройдёт всего 114 км, значит, составляем первое уравнение: 
Также по условию задачи известно, что за 6 ч движения против течения лодка проходит такой же путь, что и за 5 ч по течению, поэтому составляем второе уравнение: 
Для наглядности составим условие задачи в виде таблицы.
Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать
Решение задач с помощью систем линейных уравнений
Алгоритм решения задачи с помощью системы линейных уравнений
- Обозначить неизвестные величины переменными («от смысла к буквам»).
- По условию задачи записать уравнения, связывающие обозначенные переменные.
- Решить полученную систему уравнений.
- Истолковать результат в соответствии с условием задачи («от букв к смыслу»).
Задуманы два числа. Если от первого отнять второе, то получается 10. Если к первому прибавить удвоенное второе, то получается 91. Найдите задуманные числа.
«От смысла к буквам»:
Пусть x и y — задуманные числа.
Уравнения по условию задачи::
Решение системы уравнений:
«От букв к смыслу»:
Задуманы числа 37 и 27.
Примеры
Пример 1. Периметр прямоугольника равен 48 см. Его длина больше ширины в 3 раза.
Найдите стороны прямоугольника.
Пусть a и b — длина и ширина прямоугольника.
$$ <left< begin P = 2(a+b) = 48 \ a = 3b end right.> Rightarrow <left< begin a+b = 24 \ a = 3b end right.> Rightarrow <left< begin 3b+b = 24 \ a = 3b end right.> Rightarrow <left< begin 4b = 24 \ a = 3b end right.> Rightarrow <left< begin a = 18 \ b = 6 end right.> $$
Ответ: длина прямоугольника 18 см, ширина 6 см.
Пример 2. Два программиста из Бомбея, работающие в одном проекте, написали 100500 строк кода. Первый работал 70 дней, второй – 100 дней. Сколько строк писал каждый программист ежедневно, если за первые 30 дней первый написал на 5550 строк больше, чем второй?
Пусть x — ежедневное количество строк для 1-го программиста, y- для 2-го.
$$ <left< begin 70x+100y = 100500 |:10 \ 30x-30y = 5550 |:30 end right.> (-) Rightarrow <left< begin 7x+10y = 10050 \ x-y=185 | times 10 end right.>$$
$$ Rightarrow (+) <left< begin 7x+10y = 10050 \ 10x-10y = 1850 end right.> Rightarrow <left< begin 17x = 11900 \ y = x-185 end right.> Rightarrow <left< begin x = 700 \ y = 515 end right.> $$
Ответ: 700 строк и 515 строк
Пример 3. За 2 кг конфет и 3 кг печенья заплатили 1540 руб. Сколько стоит 1 кг конфет и 1 кг печенья, если 2 кг печенья дороже 1 кг конфет на 210 руб.?
Пусть x — цена за 1 кг конфет, y — за 1 кг печенья.
$$ <left< begin 2x+3y = 1540 \ 2y-x = 210 | times 2 end right.> Rightarrow (+) <left< begin 2x+3y = 1540 \ -2x+4y = 420 end right.> Rightarrow <left< begin 7y = 1960 \ x = 2y-210 end right.> Rightarrow <left< begin x = 350 \ y = 280 end right.> $$
Ответ: 1 кг конфет — 350 руб. и 1 кг печенья — 280 руб.
Пример 4. Катер за 3 ч движения против течения реки и 2 часа по течению проходит 73 км. Найдите собственную скорость катера и скорость течения, если за 4 ч движения по течению катер проходит на 29 км больше, чем за 3 ч движения против течения.
Пусть v — скорость катера (км/ч), u — скорость течения (км/ч).
$$ Rightarrow <left< begin 5v-u = 73 \ v+7u = 29 end right.> Rightarrow <left< begin 5(29-7u)-u = 73 \ v = 29-7u end right.> Rightarrow <left< begin 145-35u-u = 73 \ v = 29-7u end right.> Rightarrow$$
Ответ: скорость катера 15 км/ч и скорость течения 2 км/ч
Пример 5. 5 карандашей и 3 тетрадки вместе стоили 170 руб. После того, как карандаши подешевели на 20%, а тетрадки подорожали на 30%, за 3 карандаша и 5 тетрадок заплатили 284 руб. Найдите первоначальную цену карандаша и тетрадки.
Пусть x – первоначальная цена карандаша, y — тетрадки.
$$ <left< begin 5x+3y = 170 \ 3cdot0,8x+5cdot1,3y = 284 end right.> Rightarrow <left< begin 5x+3y = 170 |times frac \ 2,4x+6,5y = 284 end right.> Rightarrow (-) <left< begin 2,4x+1,44y = 81,6 \ 2,4x+6,5y = 284 end right.> $$
Ответ: карандаш сначала стоил 10 руб., тетрадка — 40 руб.
Пример 6*. Велосипедист планирует добраться из пункта А в пункт В. Если он будет ехать на 3 км/ч быстрее, чем обычно, он доберётся на 1 час раньше. А если он будет ехать на 2 км/ч медленней, чем обычно, то – на 1 час позже. Найдите обычную скорость велосипедиста и время поездки при этой скорости.
Пусть v – обычная скорость велосипедиста (км/ч), t — обычное время (ч).
Расстояние между А и В неизменно, и по условию равно:
Ответ: обычная скорость 12 км/ч, время 5 ч
Пример 7*. В одной бочке налито 12 л, во второй – 32 л. Если первую бочку доверху наполнить водой из второй, то вторая бочка будет наполнена ровно наполовину своего объёма. Если вторую бочку доверху наполнить водой из первой, то первая бочка будет наполнена на 1/6 своего объёма. Найдите объём каждой бочки.
Пусть x — объём первой бочки (л), y – объём второй (л).
Пусть a л перелито из второй бочки, и первая наполнилась до краёв, а во второй воды осталось наполовину:
Теперь пусть b л перелито из первой бочки, и вторая наполнилась до краёв, а в первой воды осталось на 1/6:
$$ <left< begin x+ frac y = 44 | times 2 \ frac x+y = 44 end right.> Rightarrow (-) <left< begin 2x+y = 88 \ frac x+y = 44 end right.> Rightarrow (+) <left< begin 1frac x = 44 \ y = 88-2x end right.> Rightarrow $$
Ответ: первая бочка 24 л, вторая – 40 л
Пример 8*. Если школьник едет в школу на автобусе, а возвращается домой пешком, то он тратит на всю дорогу полтора часа. Если он едет туда и обратно на автобусе, то он тратит полчаса. Сколько времени потратит школьник, если он пойдёт туда и обратно пешком?
Пусть s — расстояние между домом и школой, v — скорость автобуса, u — скорость школьника, t — искомое время, потраченное на дорогу туда и обратно пешком.
По условию задачи:
Из второго уравнения $ frac = frac = 0,25 $. Подставляем в первое уравнение:
И тогда искомое время:
$$ t = frac = 2cdot1,25 = 2,5 (ч) $$
Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать
Авторский учебный задачник «Решение систем линейных уравнений с двумя переменными»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
Авторский учебный задачник
Муниципального образовательного учереждения
«Специализированная школа № 115 с углубленным
изучением иностранных языков г.Донецка
Метапредметный подход обеспечивает переход от существующей практики дробления знаний на предметы к целостному образному восприятию мира, к метадеятельности. Метапредметные (компетентностные) результаты образовательной деятельности – это способы деятельности, применимые как в рамках образовательного процесса, так и при решении проблем в реальных жизненных ситуациях, освоенные обучающимися на базе одного, нескольких или всех учебных предметов. Метапредметность как принцип интеграции содержания образования, как способ формирования теоретического мышления и универсальных способов деятельности обеспечивает формирования целостной картины мира в сознании ребёнка. При таком подходе у учащихся формируется подход к изучаемому предмету как к системе знаний о мире.
Обучение школьников метапредметным знаниям требует совместного участия учителей математики и учителей предметников.
Качество современного образования всё больше связывается с так называемой функциональной грамотностью, под которой понимают способность человека адаптироваться в современном обществе, способность к самореализации, умению применять полученные в разных областях знания для решения жизненно важных задач.
Все результаты освоения учебно-методического курса образуют целостную систему вместе с предметными средствами.
Математика позволяет обеспечить формирование как предметных, так и общеучебных (метапредметных) умений школьников, которые в дальнейшем позволят им применять полученные знания и умения для решения собственных жизненных задач.
1. Повышение уровня математического развития учащихся при решении задач на составление систем линейных уравнений с двумя переменными.
2. Воспитание метапредметной грамотности учащихся с целью привития им знаний и умений анализировать практические метапредметные ситуации.
3. Выработать у учащихся активную позицию по вопросам профориентации.
Образец решения задачи
Легковой автомобиль за 3,5 часа проехал то же расстояние,
что и грузовой за 5 часов. Найдите их скорости, если известно,
что легковой автомобиль двигался на 30 км/ч быстрее грузового.
Пусть V легкового автомобиля равна х км/ч, а V грузового автомобиля равна у км/ч. Тогда за 3,5 ч легковой автомобиль проезжает S =3,5х км/ч, а грузовой автомобиль за 5 ч проезжает расстояние S =5у км/ч. Таким образом, 3,5х=5у.
Так как скорость легкового автомобиля на 30 км/ч больше скорости грузового автомобиля, то х – у = 30.
С
оставим и решим систему линейных уравнений:
х = 30 + у,
х = 30 + у,
Значит, скорость легкового автомобиля равна 100 км/ч, а скорость грузового автомобиля равна 70 км/ч.
1. Задачи от учителя русской литературы»
1.1 . Я знаю, что 2 сказа о Хозяйке Медной горы и 3 сказа о героях-детях занимают 94 страницы. А 3 сказа о Хозяйке Медной горы и и 4 сказа о героях детях занимают 133 страниц. Помогите мне узнать, сколько страниц может занимать 1 сказ о Хозяйке Медной горы и 1 сказ о героях-детя х.
1.2. Старик Кокованя приютил у себя сироту. Девочка Даренка была смышленая и чудная. Встретилась она с волшебным козлом, которого прозвали Серебряное копытце. При каждой встрече с ним можно было собрать много каменьев. При первой встрече Даренка собрала два мешочка гранатов и три мешочка малахитов, всего 1300 гр. А при второй встрече один мешочек гранатов и два мешочка малахитов, всего 800 граммов. Сколько граммов самоцветов содержится в каждом мешочке с малахитом и в каждом мешочке с гранатом?
1.3. Задача из рассказа А.П. Чехова «Репетитор» : Купец купил 138 арш. черного и синего сукна за 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное — 3 руб.?
1.4. Когда Буратино первый раз подсчитал в классе носы девочек и уши мальчиков, получилось 41. Когда он второй раз посчитал уши девочек и носы мальчиков, получилось 43. Сколько девочек и мальчиков?
1. 5. С 1574 по 1724 год было напечатано 96 изданий азбук и букварей, причем букварей на 40% больше чем азбук. Сколько изданий азбук и сколько изданий букварей было напечатано? было напечатано ?
2
. Задачи от учителя математики
2.1. Основание равнобедренного треугольника на 7 см больше его боковой стороны. Найти боковую сторону и основание треугольника, если его периметр равен 43 см.
2.2. Найти два числа, если известно, что удвоенное первое число больше второго на 37, а половина первого меньше второго на 2.
2.3. Если длину прямоугольника уменьшить на 2 м, а ширину увеличить на 4 м, то его площадь увеличится на 12 м². Если же каждую сторону уменьшить на 1 м, то площадь начального прямоугольника уменьшится на 13 м². Найти стороны данного прямоугольника.
2.4. Разность квадратов двух положительных чисел равна 275, а квадрат их разности равен 121. Найти эти числа.
2.5. Разность двух чисел равна 61. Если уменьшаемое разделить на вычитаемое, то получим 6 и остаток 1. Найдите эти числа.
3. Задачи от учителя биологии и городского эколога
3.1. В Зоопарке живет много разных животных. Среди них есть медведи – бурые и белые. Известно, что всего в зоопарке живет 9 медведей, а бурых на 5 медведей больше, чем белых. Сколько белых и бурых медведей живет в зоопарке?
3.2. В заповеднике популяция зайцев и фазанов составляет 620 особей. Когда популяция зайцев увеличилась в два раза, а популяция фазанов сократилась в 3 три раза, то количество особей стало равным 920. Сколько было зайцев и фазанов в заповеднике?
3.3. Установлено, что за вегетационный период 3 лиственных и 4 хвойных деревьев могут обезвредить 4 кг сернистого газа, причем 5 лиственных деревьев могут обезвредить на 0,5 кг больше сернистого газа, чем 3 хвойных. Сколько сернистого газа может обезвредить за вегетационный период одно лиственное и одно хвойное дерево?
4. Задачи от учителя химии и технолога металлургического завода
4.1. Из 10-процентного и 15-процентного растворов соляной кислоты требуется составить 80 г раствора, концентрация которого равна 12 %. Сколько граммов каждого раствора нужно взять?
4.2. Было две металлических отливки, одна из которых содержала 30% меди, а другая 70% меди. Сколько килограммов каждой отливки необходимо взять, чтобы получить 120 кг сплава, содержащего 40 % меди?
4.3. На металлургическом комбинате изготовили два вида отливок. 8 отливок одного вида и 6 отливок другого вида весят вместе 29 кг. Найти массу отливки каждого вида, если 4 отливки второго вида весят на 1 кг больше, чем две отливки первого вида.
4.4. За 5 тонн чугуна I сорта и 4 тонны чугуна II сорта заплатили 68 тыс. руб. После того, как чугун I сорта подешевел на 40%, а чугун II сорта подешевел на 20%, одна тонна чугуна II сорта стал дороже 1 тонны чугуна I сорта на 720 рублей. Какой была начальная стоимость чугуна каждого сорта?
4.5. Один сплав состоит из двух металлов, массы которых относятся как 2:1, а второй содержит те же металлы, но их массы относятся как 3:4. Сколько частей каждого сплава нужно взять, чтобы получить третий сплав, которых массы тех же металлов относились бы, как 5:8?
5. Задачи от учителя физкультуры и менеджера отельного бизнеса
5 .1. В двух школах 1900 учеников. В тур истическую п оездку отправились 5% уч еников о дной школы и 8% учеников другой школы, что вместе составило 125 учащихся. Сколько учеников было в каждой школ е?
5.2. Школьная баскетбольная команда в двух играх заработала 95 очков. Если удвоить количество очков, полученных в первой игре, то это на 5 меньше, чем количество очков, полученных во второй игре. Сколько очков заработала каждая команда в каждой игре?
5.3 . Во время путешествия турист проделал путь в 1100 км на самолете и на автобусе. На самолете он пролетел расстояние в 4,5 раза большее, чем проехал на автобусе. Какое расстояние турист пролетел на самолете?
5.4. Два туриста должны выйти навстречу друг другу из пунктов А и В, расстояние между которыми 30 км. Если первый выйдет на 2 часа раньше второго, то они встретятся через 2,5 часа после выхода второго туриста. Если второй выйдет на 2 часа раньше, то встреча состоится через 3 часа после выхода первого. Определите скорость движения каждого туриста.
5.5. У причала находилось 6 лодок, часть из которых была двухместными, а часть трехместными. Всего в эти лодки может поместиться 14 человек. Сколько двухместных и сколько трехместных лодок было у причала?
5.6. На турбазе имеются палатки и домики. Всего их 25. В каждом домике размещается по 4 человека, в каждой палатке — по 2 человека. Сколько палаток и сколько домиков на турбазе, если на ней отдыхает всего 70 человек?
6. Задача от школьного повара и
шеф – повара ресторана
6 .1. Масса трех блюд составляет 2,5 кг. Масса первого и второго блюда на 0,1 кг больше массы третьего блюда, а второго и третьего на 1,1 кг больше массы первого блюда. Найти массу каждого блюда.
6.2. Имеется молоко 5% жирности и 1% жирности. Сколько молока каждого вида нужно взять, чтобы получить 3 литра молока, жирность которого составит 3,2%?
6.3. За 70 кг апельсинов и 40 кг лимонов заплатили 7800 рублей. Сколько стоит 1 кг апельсинов и 1 кг лимонов, если 50 кг апельсинов дороже 20 кг лимонов на 1200 руб.?
6.4. На продовольственном складе для школьной столовой закупили 5 мешков муки и 8 мешков картошки, причем картошки на 307 кг больше, чем муки, а для ресторана 4 мешка муки и 2 мешка картошки, причем всего 334 кг. Сколько весит один мешок сахара и один мешок картошки?
6.5. В ресторане работают повара и официанты. Вчера на работу не пришли 4 официанта, и 1 повар. При этом оказалось, что поваров на 2 человека меньше, чем официантов. Сегодня не пришел 1 повар и 5 официантов. При этом оказалось, что официантов в 2 раза больше, чем поваров. Сколько всего поваров и официантов трудятся в ресторане?
7. Задачи от родителей
7.1. За 5 тетрадей и 4 шариковые ручки заплатили 68 рублей. После того, как тетради подешевели на 40%, а ручки на 20%, одна ручка стала дороже тетради на 7, 2 руб. Какова была начальная цена ручки и тетради?
7.2. Мать старше дочери на 24 года, а дочь вдвое младше матери. Сколько лет матери и сколько лет дочери?
7.3 . Сколько лет брату и сколько лет сестре, если два года назад брат был старше сестры в 2 раза, а 8 лет назад – в 5 раз?
7.4. Если рассадить гостей по двое за стол, то не хватит трех столов. Если посадить их по трое, то один стол окажется лишним. Сколько гостей и сколько столов?
7 .5. . На одно платье и 3 сарафана пошло 9м ткани, а на 3 таких же платья и 5 таких же сарафанов -19м ткани. Сколько ткани потребуется на одно платье и сколько на один сарафан?
7.6. Брат и сестра, работая летом на почте, заработали 230 0 руб. Брат заработал на 40 0 руб лей бо льше , чем сестр а . Сколько заработал каждый?
8. Задачи от директора школы
8.1. Для школьного спортзала были приобретены мячи. За 4 футбольных и 3 волейбольных мяча заплатили 2000 рублей. После того, как футбольный мяч подешевел на 20%, а волейбольный подорожал на 10%, за один футбольный и один волейбольный мяч заплатили 500 рублей. Какой была начальная цена каждого мяча?
8.2 . В двух седьмых классах – 72 ученика. Если бы из 7-А класса 2 ученика перешли в 7-Б класс, то в обоих классах учеников стало поровну. Сколько учеников в каждом классе?
8.3. Выпускники школы получили 9 медалей. Число серебряных медалей составляет 50% от числа золотых медалей. Сколько получили серебряных и сколько золотых медалей выпускники школы?
8.4. Школьная библиотека получила 55 новых учебников по математике и физике. Если бы учебников по математике было на 3 меньше, а учебников по физике было на 6 больше, то их было бы поровну. Сколько учебников физики и сколько учебников математики получила школьная библиотека?
9. Задачи от мастеров промышленных предприятий
9.1. . Двое рабочих изготовили по одинаковому количеству деталей. Первый выполнил эту работу за 5ч, а второй за 4ч, так как изготовлял в час на 12 деталей больше первого. Сколько деталей изготовил каждый рабочий?
9.2. Две бригады за месяц должны были изготовить по плану 680 деталей. Первая бригада перевыполнила месячное задание на 20%, а вторая на 15%, и поэтому обеими бригадами было изготовлено сверх плана 118 деталей. Сколько деталей должна была изготовить каждая бригада за месяц?
9.3. Двое мастеров, работая вместе, могут закончить работу за 12 дней. Если первый мастер будет работать два дня, а второй три дня, то они выполнят только 20% этой работы. За сколько дней может выполнить работу каждый мастер, работая отдельно?
9.4 . Техническое перевооружение цеха позволило выпустить в феврале на 165 изделий больше, чем в январе. Сколько изделий было выпущено в январе и сколько в феврале, если известно, что за эти месяцы цех выпустил 1315 изделий?
9.5. Два автомата изготавливают детали. Число деталей, изготовленных первым автоматом за 3 часа и вторым за 2 часа, составляет 720 штук. Четвертая часть деталей, изготовленных обоими автоматами за 2 часа, составила 150 штук. Сколько деталей изготавливает автомат за час?
10. Задачи от фермеров
10.1. Для одной лошади и двух коров выдают ежедневно 34 кг сена, а для двух лошадей и одной коровы – 35 кг сена. Сколько сена выдают ежедневно одной лошади и сколько одной корове?
10.2 . В фермерском хозяйстве по гречиху и просо отведено 19 га, причем гречиха занимает на 5 га больше, чем просо. Сколько га отведено под каждую из этих культур?
10.3. Поле площадью 100 га поделили на 2 участка так, что площадь первого на 5 га больше половины второго. Найти площадь каждого участка.
10.4. Под озимыми культурами было занято на 480 га больше, чем под яровыми. После того как убрали 80% озимых и 25% яровых культур, площадь, оставшаяся под озимыми, оказалась на 300 га меньше, чем площадь под яровыми. Какая площадь была отведена под яровые, и какая — под озимые культуры?
Ответы к задачам:
1.1. 22; 16 стр. 1.2. 300; 200 г 1.3. 63; 75 га 1.4. 14 д.; 13 м. 1.5 . 40 а; 56 б.
2.1. 12; 19 см 2.2. 26;15 2.3. 8; 6 см 2.4. 18; 7 2.5. 73;12
3.1 . 2 бур.;7 бел. 3.2. 428 з.;192 ф . 3.3. 1; 0,75 кг
4.1. 48; 32 кг 4.2. 90; 30 кг 4.3. 2,5; 1,5 кг 4.4. 8050; 6937,5 руб.
5.1. 900; 1000 уч. 5.2 . 30; 45 5.3. 900; 200 км 5.4 . 5; 3 км/ч 5.5. 4; 2 5.6. 15;10
6.1. 0,7;0,6;1,2 кг 6.2. 1,65; 1,35 л 6.3. 60;90 руб. 6.4 . 49;17 кг 6.5. 2 п.,7 оф.
7.1. 4; 12 руб. 7.2. 12; 36 лет 7.3. 18; 10 лет 7.4. 9 г.,4 ст. 7.5. 3; 2 м 7.6. 950; 1350 руб.
8.1. 350; 600 руб. 8.2. 38; 34 уч. 8.3 . 6 з.; 3 с. 8.4. 32; 23
9.1. 240 дет. 9.2. 320; 360 дет. 9.3 . 20; 30 дн. 9.4. 575; 740 изд. 9.5. 120;180 дет.
10.1. 12; 11 кг 10.2. 12; 7 га 10.3. 102,5; 97,5 га 10.4. 720 га; 1200 га
Подводя итоги, отмечу, что ведение метапредметных компетенций в образовательный процесс, это ответ системы образования на требования времени и общества, которые требуют от школы воспитания в её питомцах умения эффективно действовать за пределами учебных ситуаций и сюжето в . Учителя математики очень быстро подхватили эту идею.
Математика – это наука о фундаментальных структурах реального мира. На протяжении веков, развитие математики способствовало развитию научно – технического прогресса всего человечества. Математически образованная личность, легко применит её технологии в изучении любой новой для человека проблематике. Математика имеет широкое прикладное применение. Задача школы нашего века не предвидеть будущее, а творить его уже сегодня, вкладывая все знания, умения, профессионализм и частичку души учителей в своих учеников.
Как показывает практика, использование на уроках математики метапредметных задач позволяет показать роль и место математики в жизни каждого человека, заинтересовать учащихся предметом, повысить мотивацию изучения математики.
Общеизвестно, что нельзя двигаться вперед с головой, повернутой назад, а потому недопустимо использовать неэффективные, устаревшие технологии, изматывающие и ученика и учителя, требующие больших временных затрат и не гарантирующих качественное образование.
И, в заключении хочется привести следующие слова: «Школу можно уподобить скрипке Гварнери, из которой можно извлечь и скрип заржавевших дверных петель, и прекрасную музыку. Всё зависит от виртуозности играющего».
🎬 Видео
Урок по теме РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ 7 КЛАСССкачать
7 класс, 5 урок, Задачи на составление линейных уравнений с одной переменнойСкачать
Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать
Решение системы неравенств с двумя переменными. 9 класс.Скачать
Алгебра 7 класс (Урок№44 - Решение задач с помощью линейных уравнений.)Скачать
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Решение системы линейных уравнений графическим методом. 7 класс.Скачать
Система с тремя переменнымиСкачать
Линейное уравнение с двумя переменными. 7 класс.Скачать
АЛГЕБРА 7 класс. Решение задач с помощью систем уравненийСкачать
Решение системы линейных уравнений с двумя переменными способом сложения. 6 класс.Скачать
Урок 86. Способы решения системы линейных уравнений с двумя переменными (7 класс)Скачать
Математика. 6 класс. Решение задач с помощью составления систем линейных уравнений /14.05.2021/Скачать
Урок СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать
Решение задач на движение с помощью систем линейных уравнений с двумя переменнымиСкачать
Урок 87. Решение текстовых задач с помощью системы линейных уравнений (7 класс)Скачать
Решение задач с помощью систем уравнений, 7 классСкачать
Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать
