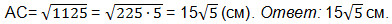Задачи на площадь прямоугольника с помощью уравнения (2 видео)

ГДЗ задачник по математике 6 класс Бунимович. Решение уравнений и задач с помощью уравнений. Номер №496

Запишите с помощью уравнения условие задачи:
а) Дорога от дома до школы проходит мимо почты. Расстояние от дома до почты на 200 м больше, чем расстояние от почты до школы. Все расстояние от дома до школы равно 1500 м. Чему равно расстояние от почты до школы?
б) Одна из сторон прямоугольника на 3 м больше другой, а его площадь равна 10

Содержание

Решение а
Решение б
8.2.3. Прямоугольник. Решение задач
Презентация по алгебре на тему «Решение задач с помощью уравнений на нахождение площади квадрата и прямоугольника»
Описание презентации по отдельным слайдам:
Краткое описание документа:
Дистанционное обучение как современный формат преподавания
Математика: теория и методика преподавания в образовательной организации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Автор материала
Дистанционные курсы для педагогов
Подарочные сертификаты
💡 Видео

Решение а

Пусть x ( м) − расстояние от почты до школы, тогда:
x + 200 (м) − расстояние от школы до почты.
Так как, все расстояние от дома до школы равно 1500 м, то:
x + x + 200 = 1500
2 x = 1500 − 200
2 x = 1300
x = 1300 : 2
x = 650 (м) − расстояние от почты до школы.
Ответ: 650 метров

Решение б

Пусть x ( м) − длина меньшей стороны прямоугольника, тогда:
x + 3 (м) − длина большей стороны прямоугольника.
Так как, площадь прямоугольника равна 10

Видео:Периметр прямоугольника равен 12,4 см, одна из его сторон на 3,8 см меньше другой....Скачать

8.2.3. Прямоугольник. Решение задач

Задача 1. Одна сторона прямоугольника меньше другой на 7 см, а диагональ прямоугольника равна 17 см. Найти периметр прямоугольника.

Решение. Пусть АВ=х. Тогда AD=х+7. Зная, что диагональ BD=17, используем теорему Пифагора и составим уравнение:

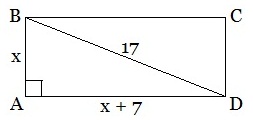
AB 2 +AD 2 =BD 2 . Получаем: х 2 +(х+7) 2 =17 2 ⇒ х 2 +х 2 +14х+49=289;

2х 2 +14х-240=0; х 2 +7х-120=0, отсюда по теореме Виета х₁=-15; х₂=8.

Следовательно, АВ=8 см, AD=8+7=15 см. Периметр прямоугольника:

P□ = 2∙(AB+AD); P□ = 2∙(8+15); P□ = 46 см. Ответ: 46 см.

Задача 2. Периметр прямоугольника 94 см, а диагональ 37 см. Найти площадь прямоугольника.

Решение. Периметр прямоугольника P□ = 2∙(AB+AD) = 94, следовательно, (AB+AD)=47. Пусть АВ=х. Тогда AD=47-х. Зная, что диагональ BD=37, используем теорему Пифагора и составим уравнение:

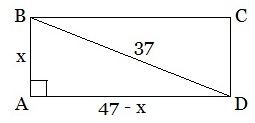
AB 2 +AD 2 =BD 2 . Получаем: х 2 +(47-х) 2 =37 2 ⇒ х 2 +47 2 -94х+ х 2 =1369;

2х 2 -94х+2209—1369=0; 2х 2 -94х+840=0. Делим обе части равенства на 2. Получаем:

х 2 -47х+420=0. Найдем дискриминант.

D=b 2 -4ac=47 2 -4∙1∙420=2209—1680=529=23 2 >0; 2 д.к.

Так как АВ=х, то либо АВ=12, тогда AD=47-12=35; либо АВ=35, тогда AD=47-35=12. Таким образом, стороны прямоугольника равны 12 см и 35 см. Площадь прямоугольника S□ = AB∙AD=12∙35=420 (см 2 ). Ответ: 420 см 2 .

Задача 3. Стороны прямоугольника относятся как 3:4, а площадь прямоугольника равна 108 см 2 . Найти диагональ прямоугольника.

Решение. Обозначим одну часть через х. Тогда АВ=3х. Тогда AD=4х.

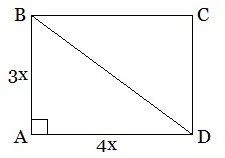
Так как S□ = AB∙AD и по условию равна 108 см 2 , то можно составить уравнение:

3х∙4х=108. Тогда 12х 2 =108, а разделив обе части равенства на 12, получаем:

х 2 =9. Отсюда х=3, так как х – положительное число. Стороны прямоугольника

Тогда АВ=3х=3∙3=9 и AD=4х=4∙3=12. Из прямоугольного треугольника BAD по теореме Пифагора найдем BD – искомую диагональ прямоугольника.

BD 2 =AB 2 +AD 2 =9 2 +12 2 =81+144=225, отсюда BD=15 см. Ответ: 15 см.

Задача 4. Биссектриса одного из углов прямоугольника делит сторону прямоугольника пополам. Найдите диагональ прямоугольника, если его меньшая сторона равна 15 см.

Решение. Итак, в прямоугольнике ABCD биссектриса АК делит сторону ВС пополам. АВ=15 см. Требуется найти диагональ АС прямоугольника. В прямоугольном треугольнике АВК один из острых углов равен 45° (биссектриса АК делит прямой угол пополам: ∠ВАК=∠КАD=45°). Тогда и второй острый угол треугольника АВК равен 45°, т.е. ∠АКВ=45°. Углы при основании ∆АВК равны, следовательно, ∆АВК – равнобедренный. Это означает, что ВК=АВ=15 см. А так как биссектриса АК по условию разделила сторону ВС пополам, то ВС=2∙ВК=30 см. Стороны прямоугольника 15 см и 30 см. Из прямоугольного треугольника АВС по теореме Пифагора найдем АС – искомую диагональ прямоугольника.

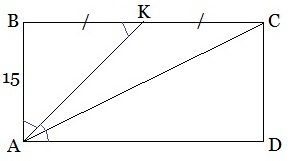
АС 2 =AB 2 +ВС 2 =15 2 +30 2 =225+900=1125, отсюда получаем:

Задача 5. В прямоугольнике точка пересечения диагоналей отстоит от меньшей стороны на 7 см дальше, чем от большей стороны. Диагональ прямоугольника равна 26 см. Найдите стороны прямоугольника.

Решение. Пусть точка О – пересечение диагоналей прямоугольника ABCD отстоит от стороны AD на х см, тогда от стороны АВ точка О будет отстоять на (х+7) см, т.е ОМ=х и ОК=х+7. Так как диагонали прямоугольника равны и точкой пересечения делятся пополам, то АО=АС:2=26:2=13 (см). Заметим, что МА=ОК. На основании теоремы Пифагора из прямоугольного треугольника АМО получаем равенство:

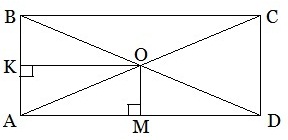
ОМ 2 +МА 2 =АО 2 или х 2 +(х+7) 2 =13 2 . Упрощаем равенство:

х 2 +х 2 +14х+49=169; 2х 2 +14х-120=0; х 2 +7х-60=0. Корни этого приведенного квадратного уравнения удобно найти по теореме Виета.

х₁=-12, х₂=5. Так как сторона выражается положительным числом, то ОМ=х=5 см. тогда ОК=5+7=12 (см). АК=ОМ=5 см и АМ=ОК=12 см – это половинки сторон прямоугольника. Тогда АВ=2∙АК=10 см и AD=2∙МА=24 см. Ответ: 10 см и 24 см.

Видео:Площадь прямоугольника. Как найти площадь прямоугольника?Скачать

Презентация по алгебре на тему «Решение задач с помощью уравнений на нахождение площади квадрата и прямоугольника»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

Здравствуйте! Классная работа 28.04.20

Тема: Решение задач с помощью уравнений на площади квадрата и прямоугольника

Цель урока: научиться решать задачи с помощью уравнений на площади квадрата и прямоугольника

стр. 215 №764 а) Пусть х (см) — сторона квадрата

Стр.212 Пример№3 Пусть х (см)-длина меньшей стороны куска стекла

Итог урока: Я умею решать задачи с помощью уравнений на площади квадрата и прямоугольника

Домашнее задание 1. Рассмотреть слайды и занести в тетрадь; 2.стр.212-213 Пример 3 ( записать решение задачи по учебнику); стр.215 №764б.

Краткое описание документа:

формирование умения решать задачи с помощь уравнения на нахождение площади квадрата и прямоугольника. Повторить формулы площадей квадрата ип прямоугольника. Решение уравнения , сводящему к линейному уравнению. Ответ на поставленный вопрос к задачи.

Позволяет активно и осознанно овладеть универсальными учебными действиями.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 932 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 682 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Сейчас обучается 308 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Алгебра 8 класс (Урок№29 - Решение задач с помощью квадратных уравнений.)Скачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 574 109 материалов в базе

Другие материалы

03.10.2020
120
0

03.10.2020
171
19

03.10.2020
326
18

02.10.2020
282
0

02.10.2020
85
1

02.10.2020
654
127

02.10.2020
728
1

02.10.2020
245
2

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

03.10.2020 81
PPTX 610 кбайт
1 скачивание
Оцените материал:

Настоящий материал опубликован пользователем Русанова Людмила Васильевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

На сайте: 6 лет
Подписчики: 0
Всего просмотров: 7284
Всего материалов: 27

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Приемная кампания в вузах начнется 20 июня

Время чтения: 1 минута

Минпросвещения подключит студотряды к обновлению школьной инфраструктуры

Время чтения: 1 минута

В Курганской области дистанционный режим для школьников продлили до конца февраля

Время чтения: 1 минута

Рособрнадзор не планирует переносить досрочный период ЕГЭ

Время чтения: 0 минут

В школах Хабаровского края введут уроки спортивной борьбы

Время чтения: 1 минута

В России могут объявить Десятилетие науки и технологий

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.