История квадратных уравнений
Необходимость решать уравнения не только первой степени, но и второй ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков, с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Правила решения этих уравнений, изложенные в вавилонских текстах, совпадает по существу с современными, но в этих текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
Решением квадратных уравнений занимались и в Древней Греции такие ученые как Диофант, Евклид и Герон. Диофант Диофант Александрийский – древнегреческий математик, живший предположительно в III веке нашей эры. Основное произведение Диофанта – «Арифметика» в 13 книгах. Евклид. Евклид древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике Герон. Герон – греческий математик и инженер впервые в Греции в I век н.э. дает чисто алгебраический способ решения квадратного уравнения
Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме: ax2 + bх = с, а> 0. (1) В уравнении (1) коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим. В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
«Обезьянок резвых стая
А двенадцать по лианам Всласть поевши, развлекалась
Стали прыгать, повисая
Их в квадрате часть восьмая
Сколько ж было обезьянок,
На поляне забавлялась
Ты скажи мне, в этой стае?»
Решение Бхаскары свидетельствует о том, что автор знал о двузначности корней квадратных уравнений. Соответствующее задаче уравнение Бхаскара пишет под видом x2 — 64x = — 768 и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 322, получая затем: x2 — б4х + 322 = -768 + 1024, (х — 32)2 = 256, х — 32= ±16, x1 = 16, x2 = 48.
Квадратные уравнения в Европе XVII века
Формулы решения квадратных уравнений по образцу Ал — Хорезми в Европе были впервые изложены в « Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Этот объемистый труд, в котором отражено влияние математики, как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из « Книги абака» переходили почти во все европейские учебники XVI — XVII вв. и частично XVIII. Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. Учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. Благодаря труда Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
Определение квадратного уравнения
Уравнение вида ax 2 + bx + c = 0, где a, b, c — числа, , называется квадратным.
Коэффициенты квадратного уравнения
Числа а, b, с – коэффициенты квадратногоуравнения.а – первый коэффициент (перед х²), а ≠ 0;b — второй коэффициент (перед х);с – свободный член (без х).
Какие из данных уравнений не являются квадратными?
1. 4х² + 4х + 1 = 0;2. 5х – 7 = 0;3. — х² — 5х – 1 = 0;4. 2/х² + 3х + 4 = 0;5. ¼ х² — 6х + 1 = 0;6. 2х² = 0;
7. 4х² + 1 = 0;8. х² — 1/х = 0;9. 2х² – х = 0;10. х² -16 = 0;11. 7х² + 5х = 0;12. -8х²= 0;13. 5х³ +6х -8= 0.
Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Применение квадратных уравнений в жизни
Презентация к открытому уроку по алгебре в 8 классе по теме » Квадратные уравнения»
Просмотр содержимого документа
«Применение квадратных уравнений в жизни»
«Квадратные уравнения в жизни»
- Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Умение решать уравнения не только имеет теоретическое значение для познания естественных законов, но и служит практическим целям.
- Важность умения решать квадратные уравнения в очередной раз доказывает то, что такие уравнения умели решать еще в древности. Но как это делалось, если в то время не существовала символическая алгебра?
История возникновения и развития квадратных уравнений
- Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.
- Квадратные уравнения решали еще в Индии. Древнеиндийский математик Баудхаяма. впервые использовал квадратные уравнения в форме ax2= c и ax2+ bx = c и привел методы их решения.
- Формулы решения квадратных уравнений в Европе были впервые изложены в 1202 г. в «Книге абака» итальянским математиком Леонардом Фибоначчи.
- Далее квадратные уравнения продолжают изучать и другие выдающиеся математики
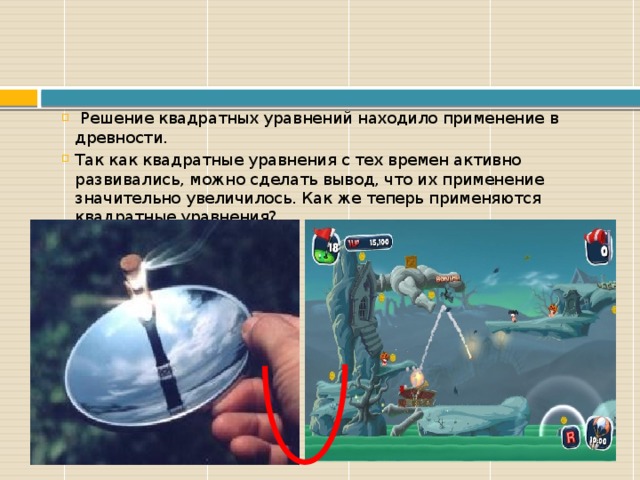
- Решение квадратных уравнений находило применение в древности.
- Так как квадратные уравнения с тех времен активно развивались, можно сделать вывод, что их применение значительно увеличилось. Как же теперь применяются квадратные уравнения?
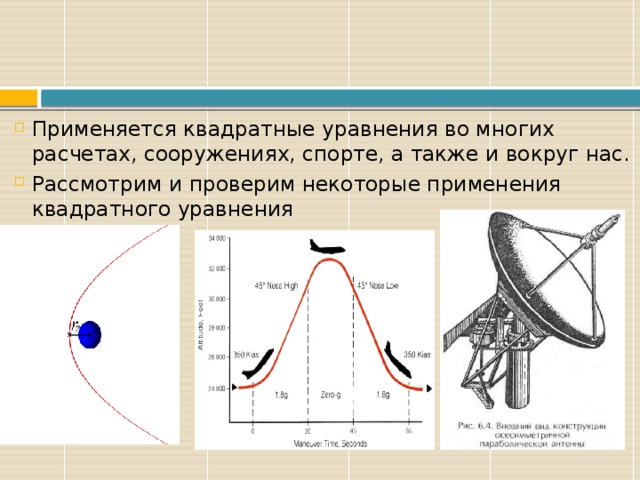
- Применяется квадратные уравнения во многих расчетах, сооружениях, спорте, а также и вокруг нас.
- Рассмотрим и проверим некоторые применения квадратного уравнения
- Сейчас ученые выяснили, что траекторию движения планет можно найти с помощью квадратного уравнения.
Взлет главная составляющая полета. Здесь берется расчет для маленького сопротивления и ускоренного взлета.
- Фонтан смотрится лучше, если капли воды достигают высоты, большей, чем высота статуи.
В данном виде спорта, крайне важны арифметические расчеты.
При разбеге прыгуна в высоту для максимально четкого попадания на планку отталкивания и высокого полета, используют расчеты связанные с парабалой.
Также подобные расчеты нужны в метании. Дальность полета объекта зависит от квадратного уравнения.
- Квадратные уравнения получили большое значение и значительное применение в жизни.
- Квадратное уравнение имеет большое применение в жизни. Еще в древности человек использовал квадратное уравнение. А с тех пор применение квадратного уравнения только росло.
- Проходя эту тему на уроке, мы мало задумываемся о практическом применении квадратных уравнений. Поэтому мы считаем, что квадратные уравнения нигде не используются, но как выяснилось это не так.
Видео:Алгебра 8 класс (Урок№29 - Решение задач с помощью квадратных уравнений.)Скачать

Исследовательская работа по теме: «Квадратные уравнения в жизни»
Видео:Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать

Скачать:
| Вложение | Размер |
|---|---|
| kvadratnye_uravneniya_v_zhizni.2_toropov_8a.pptx | 2.22 МБ |
Предварительный просмотр:
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Подписи к слайдам:
Исследовательская работа По теме: «Квадратные уравнения в жизни» Выполнил: Ученик 8 А класса Лицея №144 Торопов Алексей Руководитель: Учитель математики Иванова Светлана Борисовна
План работы: Введение . Историческая справка Актуальность выбранной темы. Гипотеза Основная часть Мои исследования Вывод Использованная литература
Цель работы: Узнать больше о квадратных уравнениях Проанализировать, где в жизни применяются квадратные уравнения
Введение. Историческая справка Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Умение решать уравнения не только имеет теоретическое значение для познания естественных законов, но и служит практическим целям. х у
Важность умения решать квадратные уравнения в очередной раз доказывает то, что такие уравнения умели решать еще в древности. Но как это делалось, если в то время не существовала символическая алгебра?
Актуальность выбранной темы. История возникновения и развития квадратных уравнений Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.
Квадратные уравнения решали еще в Индии. Древнеиндийский математик Баудхаяма . впервые использовал квадратные уравнения в форме ax 2 = c и ax 2 + bx = c и привел методы их решения.
Формулы решения квадратных уравнений в Европе были впервые изложены в 1202 г. в «Книге абака» итальянским математиком Леонардом Фибоначчи.
Далее квадратные уравнения продолжают изучать и другие выдающиеся математики Штифель Кардано Франсуа Виет Рене Декарт Ньютон
Мы уже знаем, что решение квадратных уравнений находило применение в древности. Так как квадратные уравнения с тех времен активно развивались, можно сделать вывод, что их применение значительно увеличилось. Как же теперь применяются квадратные уравнения?
Мои исследования Изучив множество источников я выяснил, что квадратное уравнение широко распространено. Оно применяется во многих расчетах, сооружениях, спорте, а также и вокруг нас. Рассмотрим и проверим некоторые применения квадратного уравнения
Сейчас ученые выяснили, что траекторию движения планет можно найти с помощью квадратного уравнения.
Взлет главная составляющая полета. Здесь берется расчет для маленького сопротивления и ускоренного взлета. Взлет самолета
Фонтан смотрится лучше, если капли воды достигают высоты, большей, чем высота статуи.
В данном виде спорта, крайне важны арифметические расчеты. П ри разбеге прыгуна в высоту для максимально четкого попадания на планку отталкивания и высокого полета, используют расчеты связанные с парабалой . Атлетика
Также подобные расчеты нужны в метании. Дальность полета объекта зависит от квадратного уравнения.
Квадратные уравнения получили большое значение и значительное применение в жизни.
С помощью исследования я выяснил, что квадратное уравнение имеет большое применение в жизни. Еще в древности человек использовал квадратное уравнение. А с тех пор применение квадратного уравнения только росло.
Вывод Проходя эту тему на уроке, мы мало задумываемся о практическом применении квадратных уравнений. Поэтому мы считаем, что квадратные уравнения нигде не используются, но как выяснилось это не так. Изучая эту тему, я узнал много интересных фактов о квадратных уравнениях, их истории, и об их применении.
Использованная литература — О.В.Зут Серия «Смотреть значит видеть» — Интернет источники, Википедия — А.А.Прокофьев «Математика» — И.Б.Кожухов «Математика» — А.М.Голова «Наука в действии»
🌟 Видео
Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Решение задач с помощью квадратных уравненийСкачать

Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

Задача на решение квадратных уравненийСкачать

Ал-Хорезми и квадратные уравненияСкачать

Квадратные уравнения. История. STEAM урокСкачать

Как решить квадратное уравнение (Положительный дискриминант)Скачать
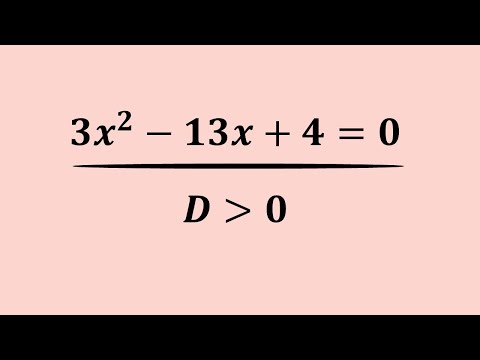
Квадратное уравнение. 1 урок.Скачать

Быстрый способ решения квадратного уравненияСкачать

Алгебра 8. Урок 12 - Задачи на составление дробно-рациональных уравнений (Часть 1)Скачать

РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ КВАДРАТНЫХ УРАВНЕНИЙ. Видеоурок | АЛГЕБРА 8 классСкачать

Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать