Задачи на движение системы уравнений

Разделы: Математика

Объяснительная записка.

В курсе алгебры 9 класса отводится всего 4 часа на решение задач с помощью систем уравнений второй степени. Это задачи на движение, совместную работу и задачи с геометрическим содержанием. Мне захотелось расширить тематику задач, и на факультативе по алгебре я предложила учащимся задачи, которые не включены в учебник. Для каждого из рассматриваемых типов задач я предлагаю алгоритм решения. Уважаемые коллеги, быть может, это покажется интересным и вам.

Алгоритм решения задач на совместную работу.

1. Принимаем всю работу, которую необходимо выполнить за 1.
   Находим производительность труда каждого рабочего в отдельности, т.е. , где t – время, за которое этот рабочий может выполнить всю работу, работая отдельно.
2. Находим ту часть всей работы, которую выполняет каждый рабочий отдельно за то время, которое он работал.
3. Составляем уравнение, приравнивая объем всей работы к сумме слагаемых, каждое из которых есть часть всей работы, выполненная отдельно каждым из рабочих.

Один комбайнер может убрать урожай пшеницы с участка на 24 ч быстрее, чем другой. При совместной работе они закончат уборку урожая за 35 часов. Сколько времени потребуется каждому комбайнеру, чтобы одному убрать урожай?

1. Принимаем площадь участка, с которого необходимо собрать урожай, за 1.

2. Пусть х – время, необходимое первому комбайнеру для уборки всего урожая, у — время, необходимое второму
комбайнеру для уборки всего урожая. Тогда– производительность первого комбайнера, – производительность второго комбайнера.
3. 35 – часть участка, с которого может убрать урожай первый комбайнер за 35 часов работы, 35 – часть участка, с которого может убрать урожай второй комбайнер за 35 часов работы.

4.Составим систему уравнений:

у = 60, х = 84
Ответ: для уборки всего урожая первому комбайнеру потребуется 84 часа, второму – 60 часов.

Две бригады, работая совместно, могут выполнить некоторое задание за 3 ч 36 мин. Сколько времени затратит на выполнение этого задания каждая бригада, работая в отдельности, если известно, что первой бригаде требуется для этого на 3 часа больше времени, чем второй.

Мастер и ученик должны были выполнить некоторое задание. После четырех дней совместной работы ученик был переведен в другой цех, и, чтобы закончить выполнение задания, мастеру пришлось еще 2 дня работать одному. За сколько дней мог бы выполнить каждый из них это задание, если известно, что мастеру для этого требуется на 3 дня меньше, чем ученику?

Алгоритм решения задач, в которых используется формула двузначного числа.

1. Вводится обозначение:
   х – цифра десятков
   у – цифра единиц
2. Искомое двузначное число 10х + у
3. Составить систему уравнений

Двузначное число в четыре раза больше суммы его цифр. Если к этому числу прибавить произведение его цифр, то получится 32. Найдите это двузначное число.

Х – цифра десятков. У – цифра единиц. 10х + у – искомое число.

2х 2 + 12х – 32 =0

х₁ =-8 (посторонний корень) х₂ =2, тогда у =4.

Задача №2.
Двузначное число в трое больше суммы его цифр. Если из этого числа вычесть произведение его цифр, то получится 13. Найдите это двузначное число. (27).

Задача №3.
Двузначное число в шесть раз больше суммы его цифр. Если это число сложить с произведением его цифр, то получится 74. Найдите это число.(54).

Задача №4.
Сумма квадратов цифр двузначного числа равна 13. Если от этого числа отнять 9, то получим число, записанное теми же цифрами, но в обратном порядке. Найти число.(32).

Задача №5.
Произведение цифр двузначного числа в три раза меньше самого числа. Если к искомому числу прибавить 18, то получится число, написанное теми же цифрами, но в обратном порядке. Найти это число.

Алгоритм решения задач на смеси.

х – масса первого раствора, у – масса второго раствора, (х + у ) – масса полученной смеси.

Найти содержание растворенного вещества в растворах, т.е.
а % от х, в % от у, с % от (х+у)

Составить систему уравнений.

Задача №1
Смешали 30% -ный раствор соляной кислоты с 10% -ным и получили 600г 15% -ого раствора. Сколько граммов каждого раствора было взято?

Введем обозначение. Пусть взяли х г первого раствора, у г – второго раствора, тогда масса третьего раствора – (х+у).

Определим количество растворенного вещества в первом, втором, третьем растворах, т.е. найдем 30% от х, 10% от у, 15% от 600.

Составим систему уравнений:


0,3х + 60 – 0,1х = 90
0,2х = 30
х = 30:0,2
х = 150, у = 600 – 150 = 450
Ответ: взяли 150 г первого раствора и 450 г второго раствора.

Задача №2
Имеется лом стали двух сортов с содержанием никеля 5% и 40%. Сколько нужно взять металла каждого их этих сортов, чтобы получить 140 т стали с содержанием 30% никеля?

Задача №3
Смешали 10% -ный и 25% -ный растворы соли и получили 3 кг 20% -ного раствора. Какое количество каждого раствора в килограммах было использовано?

Литература:

1. В.С. Крамор. Повторяем и систематизируем школьный курс алгебры и начал анализа. “ Просвещение”.
2. М.Б.Миндюк, Н.Г. Миндюк. Разноуровневые дидактические материалы по алгебре. 9 класс. “Генжер”.

3. М.И. Сканави. Сборник задач по математике для поступающих во втузы. “ Высшая школа”.

4. М.Л. Галицкий, А.М. Гольдман, Л.И. Звавич. Сборник задач по алгебре.

Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

Решение задач на движение с помощью систем линейных уравнений

Презентация по решению задач на движение с помощью систем линейных уравнений. В презентации использованы фрагменты сборника визуализированных задач к учебнику 7 класса под ред. А.Г.Мерзляк, В.М.Поляков, разработанных Смирновой Ириной Сергеевной, учителем информатики лицея № 86 г.Ярославля.

Просмотр содержимого документа
«Решение задач на движение с помощью систем линейных уравнений»

Решение задач с помощью систем линейных уравнений.

Показать (2) 2 » width=»640″

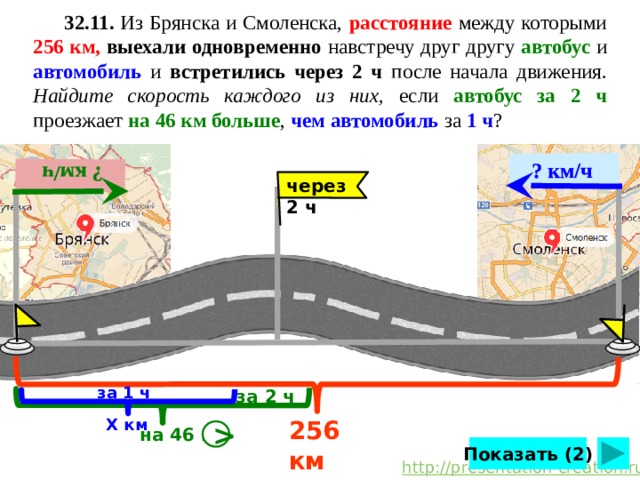
32.11. Из Брянска и Смоленска, расстояние между которыми 256 км, выехали одновременно навстречу друг другу автобус и автомобиль и встретились через 2 ч после начала движения. Найдите скорость каждого из них, если автобус за 2 ч проезжает на 46 км больше , чем автомобиль за 1 ч ?

А.Г.Мерзляк, В.М.Поляков 7 класс. №32.11 стр.225. Сделайте клик по кнопке «Показать» ( 2 раза)

Из Брянска и Смоленска, расстояние между которыми 256 км , выехали одновременно навстречу друг другу автобус и автомобиль и встретились через 2 ч после начала движения. Найдите скорость каждого из них, если автобус за 2 ч проезжает на 46 км больше , чем автомобиль за 1 ч ?

Первый этап . Составляем математическую модель задачи

Обозначим скорость автобуса – х км/ч, а скорость автомобиля — у км/ч. Автобус проезжает за 2 часа на 46 км больше, чем автомобиль за 1 час..

Составим и решим систему уравнений:

Из Брянска и Смоленска, расстояние между которыми 256 км , выехали одновременно навстречу друг другу автобус и автомобиль и встретились через 2 ч после начала движения. Найдите скорость каждого из них, если автобус за 2 ч проезжает на 46 км больше , чем автомобиль за 1 ч ?

Второй этап . Решаем систему линейных уравнений

Значит, скорость автобуса 58 км/ч, скорость автомобиля 70 км/ч.

Ответ: скорость автобуса 58 км/ч, скорость автомобиля 70 км/ч.

32.12. С двух станций, расстояние между которыми 300 км , одновременно навстречу друг другу отправились пассажирский и товарный поезда, которые встретились через 3 ч после начала движения. Если бы пассажирский поезд вышел на 1 ч раньше , чем товарный, то они встретились бы через 2,4 ч после выхода товарного поезда . Найдите скорость каждого поезда.

А.Г.Мерзляк, В.М.Поляков 7 класс. №32.12 стр.225. Сделайте клик по кнопке «Показать» (3 раза)

С двух станций, расстояние между которыми 300 км , одновременно навстречу друг другу отправились пассажирский и товарный поезда, которые встретились через 3 ч после начала движения. Если бы пассажирский поезд вышел на 1 ч раньше , чем товарный, то они встретились бы через 2,4 ч после выхода товарного поезда . Найдите скорость каждого поезда.

Составим и решим систему уравнений:

С двух станций, расстояние между которыми 300 км , одновременно навстречу друг другу отправились пассажирский и товарный поезда, которые встретились через 3 ч после начала движения. Если бы пассажирский поезд вышел на 1 ч раньше , чем товарный, то они встретились бы через 2,4 ч после выхода товарного поезда . Найдите скорость каждого поезда.

Значит, скорость пассажирского поезда 60 км/ч, скорость товарного – 40 км/ч.

Ответ: скорость пассажирского поезда 60 км/ч, скорость товарного – 40 км/ч.

8 » width=»640″

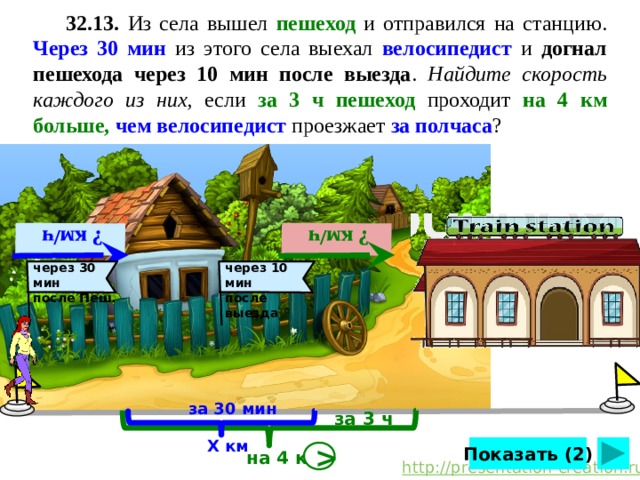
32.13. Из села вышел пешеход и отправился на станцию. Через 30 мин из этого села выехал велосипедист и догнал пешехода через 10 мин после выезда . Найдите скорость каждого из них, если за 3 ч пешеход проходит на 4 км больше, чем велосипедист проезжает за полчаса ?

А.Г.Мерзляк, В.М.Поляков 7 класс. №32.13 стр.226. Сделайте клик по кнопке «Показать» ( 2 раза)

Из села вышел пешеход и отправился на станцию. Через 30 мин из этого села выехал велосипедист и догнал пешехода через 10 мин после выезда . Найдите скорость каждого из них, если за 3 ч пешеход проходит на 4 км больше , чем велосипедист проезжает за полчаса ?

Видео:Задачи на движение | Математика TutorOnlineСкачать

Задание разного уровня сложности по теме : «Системы уравнений в задачах на скорость».
учебно-методический материал

Задание разного уровня сложности по теме : «Системы уравнений в задачах на скорость».

Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

Скачать:

Видео:Решение графических задач на равномерное движениеСкачать

Предварительный просмотр:

Задание разного уровня сложности по теме : «Системы уравнений в задачах на скорость».

1 уровень сложности

2 уровень сложности

3 уровень сложности

Из двух городов, расстояние между которыми 700 км, одновременно навстречу друг другу отправляются два поезда и встречаются через 5 часов.

Если второй поезд отправится на 7 ч раньше первого, то они встретятся через 2 ч после отправления первого поезда. Найдите скорость каждого поезда.

Из двух городов, расстояние между которыми 700 км, одновременно навстречу друг другу отправляются два поезда и встречаются через 5 часов.

Если второй поезд отправится на 7 ч раньше первого, то они встретятся через 2 ч после отправления первого поезда. Найдите скорость каждого поезда.

Из двух городов, расстояние между которыми 700 км, одновременно навстречу друг другу отправляются два поезда и встречаются через 5 часов.

Если второй поезд отправится на 7 ч раньше первого, то они встретятся через 2 ч после отправления первого поезда. Найдите скорость каждого поезда.

Дополни недостающие элементы решения задачи:

🔥 Видео

Урок по теме РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ 7 КЛАСССкачать

ОГЭ Задание 22 Задача на движение Система уравненийСкачать

Алгебра 8. Урок 12 - Задачи на составление дробно-рациональных уравнений (Часть 1)Скачать

Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

ОГЭ Задание 22 Задача на движение Система уравненийСкачать

Математика | ЗАДАЧА 22 из ОГЭ. Задачи на работуСкачать

Задачи на движение по воде | Математика | TutorOnlineСкачать

Задачи на движение. Вебинар | МатематикаСкачать

ОГЭ Задание 22 Задача на движение Система уравнений 7 классСкачать

Задачи на движение. Учимся решать задачи на движение. Способы решения задач на движение.Скачать

Задачи на решение систем уравнений 3Скачать

Траектория и уравнения движения точки. Задача 1Скачать

ЕГЭ Задание 11 Задача на движение Система уравненийСкачать

Урок 11. Решение текстовых задач. Задачи на движение, задачи на работу. Вебинар | МатематикаСкачать

Задачи на движение двух объектовСкачать

Решение задач с помощью уравнений.Скачать