Задача на уравнение бойля мариотта

Задача 28.
При 17°С некоторое количество газа занимает объем 580 мл. Какой объем займет это же количество газа при 100°С, если давление его останется неизменным?
Решение:
По закону Гей – Люссака при постоянном давлении объём газа изменяется прямо пропорционально абсолютной температуре (Т):

V₂ – искомый объём газа;
T₂ – соответствующая V₂ температура;
V₁ – начальный объём газа при соответствующей температуре Т₁.

По условию задачи V₁ = 580мл; Т1 = 290К (273 + 17 = 290) и Т₂ = 373К (273 + 100 = 373). Подставляя эти значения в выражение закона Гей – Люссака, получим:

Ответ: V₂ = 746мл.

Задача 29.
Давление газа, занимающего объем 2,5л, равно 121,6 кПа (912мм рт. ст.). Чему будет равно давление, если, не изменяя температуры, сжать газ до объема в 1л?
Решение:
Согласно закону Бойля – Мариотта, при постоянной температуре давление, производимое данной массой газа, обратно пропорционально объёму газа:

Обозначив искомое давление газа через Р₂, можно записать:

Ответ: Р₂ = 304кПа (2280мм.рт.ст.).

Задача 30. На сколько градусов надо нагреть газ, находящийся в закрытом сосуде при 0 °С, чтобы давление его увеличилось вдвое?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально температуре:

По условию задачи Т₁ = 0 °С + 273 = 273К; давление возросло в два раза: Р₂ = 2Р₁.

Подставляя эти значения в уравнение, находим:

Ответ: Газ нужно нагреть на 273 0 С.

Задача 31.
При 27°С и давлении 720 мм.рт. ст. объем газа равен 5л. Кой объем займет это же количество газа при 39°С и давлении 104кПа?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:

где Р и V — давление и объём газа при температуре Т; Р₀ и V₀ – давление и объём газа при нормальных условиях. Данные задачи: V = 5л; Т = 298К (273 + 25 = 298); Р = 720 мм.рт.ст. (5,99 кПа); Р₀ = 104 кПа; Т = 312К (273 + 39 = 312); Т = 273К. Подставляя данные задачи в уравнение, получим:

Задача 32.
При 7°С давление газа в закрытом сосуде равно 96,0 кПа. Каким станет давление, если охладить сосуд до —33 °С?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:

Обозначим искомое давление через Р₂, а соответствующую ему температуру через Т_2. По условию задачи Р₁ = 96,0 кПа; Т1 = 280К (273 + 7 = 280); Т₂ = 240К (273 – 33 = 240). Подставляя эти значения в уравнение, получим:

Ответ: Р₂ = 82,3кПа.

Задача 33.
При нормальных условиях 1г воздуха занимает объем 773 мл. Какой объем займет та же масса воздуха при 0 °С и )и давлении, равном 93,3 кПа (700мм. рт. ст.)?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:

где Р и V — давление и объём газа при температуре Т; Р₀ и V₀ – давление и объём газа при нормальных условиях. Данные задачи: Р₀ = 101,325кПа; V₀ = 773мл; Т₀ = 298К (273 + 25 = 298); Т = 273К; Р = 93,3кПа. Подставляя данные задачи и преобразуя уравнение, получим:

Ответ: V = 769, 07 мл.

Задача 34.
Давление газа в закрытом сосуде при 12°С равно 100 кПа (750мм рт. ст.). Каким станет давление газа, если нагреть сосуд до 30°С?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:

Обозначим искомое давление через Р₂, а соответствующую ему температуру через Т₂. По условию задачи Р₁ = 100 кПа; Т₁ = 285К (273 + 12 = 285); Т₂ = 303К (273 + 30 = 303). Подставляя эти значения в уравнение, получим:

Ответ: Р₂ = 106,3кПа.

Задача 35.
В стальном баллоне вместимостью 12л находится при 0°С кислород под давлением 15,2 МПа. Какой объем кислорода, находящегося при нормальных условиях можно получить из такого баллона?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:

где Р и V — давление и объём газа при температуре Т; Р₀ и V₀ – давление и объём газа при нормальных условиях. Данные задачи: V = 12л; Т = 273К (273 + 0 = 2273); Р =15,2МПа); Р₀ = 101,325кПа; Т₀ = 298К (273 + 25 = 298). Подставляя данные задачи в уравнение, получим:

Ответ: V₀ = 1,97м 3 .

Задача 36.
Температура азота, находящегося в стальном баллоне под давлением 12,5 МПа, равна 17°С. Предельное давление для баллона 20,3МПа. При какой температуре давление азота достигнет предельного значения?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:

Обозначим искомое давление через Р_2, а соответствующую ему температуру через Т₂. По условию задачи Р₁ = 12,5МПа; Т₁ = 290К (273 + 17 = 290); Р₂ = 20,3МПа. Подставляя эти значения в уравнение, получим:

Ответ: Т₂ = 198 0 С.

Задача 37.
При давлении 98,7кПа и температуре 91°С некоторое количество газа занимает объем 680 мл. Найти объем газа при нормальных условиях.
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:

где Р и V — давление и объём газа при температуре Т; Р₀ и V₀ – давление и объём газа при нормальных условиях. Данные задачи: Р₀ = 101,325кПа; V = 680мл; Т₀ = 298К (273 + 25 = 298); Т = 364К (273 + 91 = 364); Р = 98,7кПа. Подставляя данные задачи и преобразуя уравнение, получим:

Ответ: V₀ = 542,3мл.

Задача 38.
При взаимодействии 1,28г металла с водой выделилось 380 мл водорода, измеренного при 21°С и давлении 104,5кПа (784мм рт. ст.). Найти эквивалентную массу металла.
Решение:
Находим объём выделившегося водорода при нормальных условиях, используя уравнение:

где Р и V — давление и объём газа при температуре Т = 294К (273 +21 = 294); Р₀ = 101,325кПа; Т₀ = 273К; Р = 104,5кПа. Подставляя данные задачи в уравнение,

Согласно закону эквивалентов, массы (объёмы) реагирующих друг с другом веществ m₁ и m₂ пропорциональны их эквивалентным массам (объёмам):

Мольный объём любого газа при н.у. равен 22,4л. Отсюда эквивалентный объём водорода равен 22,4 : 2 = 11,2л или 11200 мл. Тогда, используя формулу закона эквивалентов, рассчитаем эквивалентную массу металла:

Ответ: m_Э(Ме) = 39,4г/моль.

Задача 39.
Как следует изменить условия, чтобы увеличение массы данного газа не привело к возрастанию его объема: а) понизить температуру; б) увеличить давление; в) нельзя подобрать условий?
Решение:
Для характеристики газа количеством вещества (n, моль) применяется уравнение РV = nRT, или — это уравнение Клапейрона-Менделеева. Оно связывает массу (m, кг); температуру (Т, К); давление (Р, Па) и объём (V, м 3 ) газа с молярной массой (М, кг/моль).

Тогда из уравнения Клапейрона-Менделеева объём газа можно рассчитать по выражению:

Отсюда следует, что V = const, если при увеличении массы (m) газа на некоторую величину будет соответственно уменьшена температура (T) системы на некоторое необходимое значение. Объём системы также не изменится при постоянной температуре, если при увеличении массы (m) газа на некоторую величину будет соответственно увеличено давление (P) системы на необходимую величину.

Таким образом, при увеличении массы газа объём системы не изменится, если понизить температуру системы или же увеличить давление в ней на некоторую величину.

Ответ: а); б).

Задача 40.
Какие значения температуры и давления соответствуют нормальным условиям для газов: а) t = 25 °С, Р = 760 мм. рт. ст.; б) t = 0 °С, Р = 1,013 • 10 5 Па; в) t = 0°С, Р = 760 мм. рт. ст.?
Решение:
Состояние газа характеризуется температурой, давлением и объёмом. Если температура газа равна 0 °С (273К), а давление составляет 101325 Па (1,013 • 10 5 ) или 760 мм. рт. ст., то условия, при которых находится газ, принято считать нормальными.

Видео:Решение задач по теме: закон Бойля-МариоттаСкачать

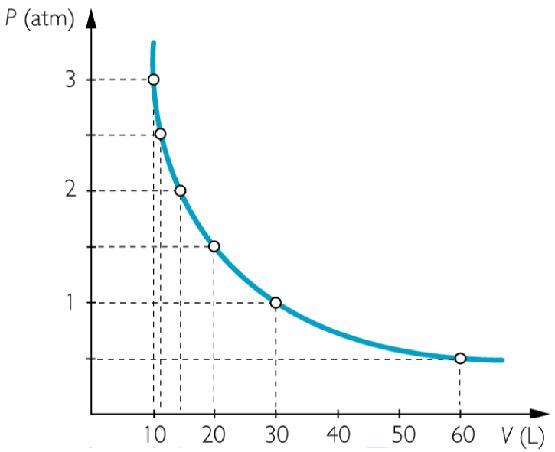
Закон Бойля-Мариотта: формула и пример задачи

При изучении газового состояния вещества в современной физике используют сравнительно простую модель. Она базируется на принципах молекулярно-кинетической теории, предложенной в середине XVIII века Даниилом Бернулли. В рамках этой модели исследуется поведение систем во время разных преобразований. В данной статье приведем формулу закона Бойля-Мариотта и название изопроцесса, к которому он применим.

Видео:Основы молекулярной физики | закон Бойля МариоттаСкачать

Модель идеального газа

Она основана на теории, которая полагает молекулы и атомы материальными точками, движущимися во всех направлениях с одинаковой скоростью. Кинетическая энергия частиц системы обуславливает наличие температуры в ней, а их постоянные столкновения со стенками сосуда приводят к возникновению давления. Считается, что в идеальной газовой модели частицы системы не взаимодействуют друг с другом, то есть их потенциальная энергия равна нулю.

Вам будет интересно: Прекрасное — это . Значение слова, синонимы и антонимы

Поведение любого реального газа хорошо описывается этой теорией только в том случае, если он образован химически инертными молекулами или атомами, его давление является невысоким, а температура находится в пределах комнатной или превышает ее.

Видео:Решение задачи на закон Бойля- МариоттаСкачать

Закон Бойля-Мариотта: формула и формулировка

Во второй половине XVII века француз Эдм Мариотт и англичанин Роберт Бойль независимо друг от друга установили следующее соотношение между давлением P и объемом V газовой системы:

Это равенство выполнялось с высокой точностью для всех исследуемых газов только в том случае, если поддерживалась постоянной температура t. В физике такой процесс называется изотермическим. Соответствующим графиком для него будет изотерма P(V).

Из формулы закона Бойля-Мариотта следует, что при изотермическом изменении одного равновесного состояния на другое давление в системе возрастает (уменьшается) ровно во столько раз, во сколько уменьшается (увеличивается) ее объем.

Хотя рассматриваемый закон был получен экспериментально, в настоящее время он может быть легко выведен из уравнения состояния идеального газа (закон Клапейрона-Менделеева), который имеет форму:

Если рассматривается закрытая система (количество вещества n=const), то во время изотермического процесса в ней (t=const) правая часть равенства не будет изменяться, а значит, левая также будет оставаться постоянной, то есть мы приходим к формуле закона Бойля-Мариотта. Величина R здесь — это универсальная газовая константа.

Пример графика, соответствующего рассматриваемому закону, приведен выше. Кривая P(V) называется изотермой и представляет собой гиперболу.

Видео:Закон Бойля Мариотта в действииСкачать

Пример задачи

Покажем, как следует пользоваться формулой закона Бойля-Мариотта для решения задач.

Известно, что в результате изотермического процесса давление в системе с идеальным газом уменьшилось с 105 Па до 104 Па. Насколько изменился ее объем при этом, если в начале процесса он был равен 10 литрам.

Запишем закон изотермического расширения газа в следующей форме:

Отсюда можно выразить значение объема V2 и вычислить его:

V2 = 105/104*10 = 100 литров.

Отметим, что при вычислении объема мы не переводили данные в систему СИ, поскольку единицы измерения давления сократились. Осталось найти разницу между конечным и начальным объемом, чтобы получить ответ на вопрос задачи: V2 — V1 = 90 литров.

Видео:Закон идеальных газов. Практическая часть - решение задачи. 9 класс.Скачать

§ 3.12. Примеры решения задач

Задачи на применение газовых законов очень разнообразны. Для их решения нельзя указать какой-либо один определенный прием. Полезными могут оказаться следующие советы.

1. Если согласно условию задачи один из трех параметров (р, V или Т) постоянный, то при Т = const надо применять закон Бойля—Мариотта (3.5.2), при р = const — закон Гей-Люссака (3.7.7), а при V = const — закон Шарля (3.10.2) или (3.10.3).

1. Если изменяются все три параметра, то следует воспользоваться уравнением состояния в форме (3.9.9) или (3.9.5).

   Уравнение состояния (3.9.9) применяется в тех случаях, когда известна масса газа и часть макроскопических параметров в определенном состоянии газа и надо найти неизвестные величины.

2. Для определения давления смеси газов, не вступающих в химические реакции, используют закон Дальтона (3.8.2).
3. Во многих задачах требуется построение графиков, изображающих разного рода процессы. Для этого нужно знать зависимость параметров друг от друга, которая в общем случае дается уравнением состояния, а в частных — газовыми законами.
4. При решении большинства задач надо четко представлять себе, каково начальное состояние системы и какой процесс переводит его в конечное состояние.

Как измерить медицинским термометром температуру тела человека, если температура окружающего воздуха +42 °С?

Решение. Можно предварительно охладить термометр в холодильнике. Если холодильника нет, то нужно подержать термометр 5—8 мин под мышкой, извлечь его и сразу же стряхнуть. Термометр покажет температуру тела, так как ртуть в термометре сожмется при контакте с телом до объема, соответствующего температуре тела.

Газ в цилиндрическом сосуде разделен на две равные части подвижным поршнем, имеющим массу m и площадь сечения S. При горизонтальном положении цилиндра давление газа в каждой половине сосуда равно р. Определите давление р₁ газа над поршнем при вертикальном положении цилиндра. Температуру газа считать постоянной.

Решение. При горизонтальном положении цилиндра объем каждой его части обозначим через V (эти объемы равны). При вертикальном положении цилиндра объем верхней части станет равным V + ΔV, а нижней V — ΔV. Давление в нижней части цилиндра станет равным . Согласно закону Бойля— Мариотта

Исключив из этих равенств , получим квадратное уравнение для p₁:

Второй корень квадратного уравнения отрицателен и потому лишен физического смысла.

Поршневой насос при каждом качании захватывает воздух объемом V₀. При откачке этим насосом воздуха из сосуда объемом V насос совершил п качаний. Затем другой насос с тем же рабочим объемом V₀ начал нагнетать воздух из атмосферы в тот же сосуд, совершив также п качаний. Какое давление установится в сосуде? Температуру воздуха во время работы насоса считать постоянной.

Решение. Согласно закону Бойля—Мариотта при откачке воздуха из сосуда после первого качания давление в сосуде станет равным , где p₀— атмосферное давление.

После второго качания будет выполняться равенство p₁V = p₂(V + V₀) и, следовательно, и т.д. После n качаний в сосуде установится давление

При нагнетании воздуха в сосуд после n качаний давление станет равным

При любом n р > р₀, так как во время нагнетания воздуха при каждом качании насос захватывает воздух, имеющий атмосферное давление р₀, а при откачке при каждом качании удаляется воздух при давлении, меньшем р₀.

В запаянной с обоих концов цилиндрической трубке находится воздух при нормальных условиях. Трубка разделена подвижным поршнем на две части, объемы которых V₁ и V₂ относятся как 1 : 2. До какой температуры t₁ следует нагреть воздух в меньшей части трубки и до какой t₂ охладить в большей, чтобы поршень делил трубку на две равные части, если нагревание и охлаждение в обеих частях трубки производятся при условии = const?

Решение. Условие = const означает, что процессы нагревания и охлаждения происходят изобарно. При отношении начальных объемов эти объемы составляют и , где V₀ — объем всей трубки. Конечные объемы обеих частей одинаковы и равны .

Согласно закону Гей-Люссака для воздуха в меньшей части трубки выполняется соотношение

а для воздуха в большей части

где Т₀ = 273 К — температура, соответствующая начальным условиям. Отсюда

В цилиндре под поршнем находится воздух при давлении p₁ = 2 • 10 5 Па и температуре t₁ = 27 °С. Определите массу m груза, который нужно положить на поршень после нагревания воздуха до температуры t₂ = 50 °С, чтобы объем воздуха в цилиндре стал равен первоначальному. Площадь поршня S = 30 см 2 .

Решение. Так как в процессе нагревания объем воздуха в цилиндре не изменяется, то согласно закону Шарля имеем

Подставляя в (3.12.1) выражение для р₂, получим

Найдите среднюю (эффективную) молярную массу сухого атмосферного воздуха, предполагая известный процентный состав воздуха по массе: азот — n₁ = 75,52%, кислород — n₂ = 23,15%, аргон — n₃ = 1,28% и углекислый газ — n₄ = 0,05%.

Решение. Для каждого газа можно записать уравнение состояния:

Здесь M₁, M₂, M₃ и M₄ — молярные массы соответственно азота, кислорода, аргона и углекислого газа.

Складывая правые и левые части этих уравнений, получим

Для смеси газов выполняется соотношение

где m = m₁ + m₂ + m₃ + m₄ — масса воздуха с объемом V, а М — искомая эффективная молярная масса. Согласно закону Дальтона

Сравнивая уравнения состояния (3.12.2) и (3.12.3), получим

Разделив числитель и знаменатель на m и умножив на 100%, получим выражение для М через процентный состав воздуха по массе

Закрытый с обоих концов цилиндр наполнен газом при давлении p = 100 кПа и температуре t = 30 °С и разделен подвижным теплонепроницаемым поршнем на две равные части длиной L по 50 см. На какую величину ΔT нужно повысить температуру газа в одной половине цилиндра, чтобы поршень сместился на расстояние l = 20 см, если во второй половине цилиндра температура не изменяется? Определите давление газа после смещения поршня.

Решение. Для газа в части цилиндра с постоянной температурой применим закон Бойля—Мариотта:

где S — площадь основания цилиндра. Для нагреваемой части цилиндра запишем уравнение Клапейрона:

В уравнениях (3.12.4) и (3.12.5) р₁ — давление газа после смещения поршня, одинаковое в обеих частях цилиндра вследствие равновесия поршня, а Т + ΔT в уравнении (3.12.5) — температура газа в нагретой части цилиндра.

Разделив почленно уравнение (3.12.4) на уравнение (3.12.5), получим

Из уравнения (3.12.4) находим p₁:

Сосуд объемом V = 100 л разделен пополам полупроницаемой перегородкой. В начальный момент времени в одной половине сосуда находился водород, масса которого m₁ = 2 г, а во второй — 1 моль азота. Определите давления, установившиеся по обе стороны перегородки, если она может пропускать только водород. Температура в обеих половинах одинакова и постоянна: t = 127 °С.

Решение. Так как водород свободно проходит через перегородку, то он распространяется по всему сосуду. Запишем уравнение Менделеева—Клапейрона для водорода после установления состояния равновесия:

где М₁ = 2 • 10 -3 кг/моль — молярная масса водорода.

В той части сосуда, в которой вначале был только водород, он и в дальнейшем останется в чистом виде, так что давление в этой части сосуда станет равным

Для азота уравнение Менделеева—Клапейрона имеет вид

где р₂ — давление азота.

Так как в этой половине находятся водород и азот, то полное давление р согласно закону Дальтона складывается из парциальных давлений р₁ и р₂, т. е.

Гелий массой 20 г, заключенный в теплоизолированном цилиндре под поршнем, медленно переводится из состояния 1 с объемом V₁ = 32 л и давлением р₁ = 4,1 атм в состояние 2 с объемом V₂ = 9 л и давлением р₂ = 15,5 атм. Какой наибольшей температуры достигнет газ при этом процессе, если на графике зависимости давления газа от объема процесс изображается прямой линией (рис. 3.18)?

Решение. Как следует из рисунка 3.18, давление и объем газа связаны линейной зависимостью: р = aV + b, где а и b — постоянные коэффициенты. Из условий задачи получаем систему уравнений

Решив эту систему относительно а и b, найдем

Подставив в уравнение Менделеева—Клапейрона вместо р выражение aV + b, получим

График зависимости Т от V представляет собой параболу (рис. 3.19).

Кривая достигает максимума при V_max = = 20 л, когда корни квадратного уравнения (3.12.6) совпадают. При этом

На рисунке 3.20 изображен график изменения состояния идеального газа в координатах р, V. Начертите графики этого процесса в координатах V, Т и р, Т.

Решение. Из рисунка 3.20 следует, что давление газа р и его объем V находятся в прямой пропорциональной зависимости

где k — постоянный коэффициент. Подставив значение давления (3.12.7) в уравнение Менделеева— Клапейрона, получим

Уравнение (3.12.8) — это уравнение параболы, ось симметрии которой совпадает с осью Т. Следовательно, в координатах V, Т искомый график имеет вид, показанный на рисунке 3.21, а. Аналогично получим график этого процесса в координатах p, T (рис. 3.21, б).

Упражнение 2

1. Вы надули щеки. При этом и давление, и объем воздуха во рту увеличиваются. Как это согласуется с законом Бойля— Мариотта?
2. Чтобы измерить температуру человеческого тела, приходится держать термометр под мышкой в течение 5—8 мин. В то же время стряхнуть его можно практически сразу после измерения температуры. Почему?
3. Узкая вертикальная трубка длиной L, закрытая с одного конца, содержит воздух, отделенный от наружного воздуха столбиком ртути длиной h. Плотность ртути равна ρ. Трубка расположена открытым концом вверх. Какова была длина l столбика воздуха в трубке, если при перевертывании трубки открытым концом вниз из трубки вылилась половина ртути? Атмосферное давление равно р₀.
4. В ртутный барометр попал пузырек воздуха, вследствие чего барометр показывает давление меньше истинного. При давлении р₁ = 768 мм рт. ст. уровень ртути расположен на высоте h₁ = 748 мм, причем длина пустой части трубки l = 80 мм. Каково атмосферное давление р₂, если ртуть стоит на высоте h₂ = 734 мм? Плотность ртути ρ = 1,36 • 10 4 кг/м 3 .
5. Площадь сечения цилиндра автомобильного насоса S = 10 см 2 . Определите длину l цилиндра, если известно, что для накачки шины объемом V = 0,02 м 3 от давления р₀ = 1 • 10 5 Па до давления р = 3 • 10 5 Па требуется совершить n = 100 качаний. Утечкой и нагреванием воздуха пренебречь.
6. В цилиндре под поршнем находится воздух. Поршень имеет форму, показанную на рисунке 3.22. Масса поршня m = 6 кг, площадь сечения цилиндра S = 20 см 2 . Атмосферное давление р₀ = 10 5 Па. Найдите массу m₁ груза, который надо положить на поршень, чтобы объем V₁ воздуха в цилиндре уменьшился в 2 раза. Трение не учитывать. Температура постоянна.

Рис. 3.22

1. Два сосуда объемом V₁ = 200 см 3 и V₂ = 100 см 3 , наполненные кислородом при температуре t = 27 °С под давлением p₀ = 760 мм рт. ст., соединены трубкой, внутри которой находится теплоизолирующая пористая перегородка, обеспечивающая одинаковость давлений в сосудах. Затем первый сосуд нагрели до температуры t₁ = 100 °С, а второй охладили до температуры t₂ — 0 °С. Определите установившееся в системе давление.
2. Изобразите на графиках в координатах р, V; р, Т и V, Т изотермический процесс для одного моля газа при Т = Т₁ и Т = 2Т₁.
3. Изобразите на графиках в координатах р, V; р, Т и V, T изобарный процесс: 1) для р =р₁ и p = 2p₁, если v = 1 моль; 2) для р = р₁, если v = 3 моль.
4. На рисунке 3.24 показан график изменения состояния идеального газа в координатах р, V. Представьте этот процесс на графиках в координатах V, Ти р, Т.

   📹 Видео

   ЛР-10-2-01 Проверка закона Бойля-МариоттаСкачать

   

   Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

   

   Газовые законыСкачать

   

   №162. Неорганическая химия. Тема17. Основные законы химии. Часть17. Закон Бойля-Мариотта,Гей-ЛюссакаСкачать

   

   Уравнения и графики Изотермического Процесса.Закон Бойля-Мариотта.Каргту.Ис19-3Скачать

   

   Газовые законы. Изопроцессы | Физика 10 класс #34 | ИнфоурокСкачать

   

   закон бойля мариоттаСкачать

   

   мкт ИЗОТЕРМИЧЕСКИЙ процесс ИЗОХОРНЫЙ процесс ИЗОБАРНЫЙ процессСкачать

   

   Физика для чайников. Урок 26. Закон Бойля-МариоттаСкачать

   

   7 8 МОЛЕКУЛЯРНАЯ ФИЗИКА Закон Бойля МариоттаСкачать

   

   Доказать неравенство ➜ a⁴+b⁴+c⁴+d⁴≥4abcd ➜ Задача от ВМК МГУСкачать

   

   Урок 158. Задачи на газовые законы - 1Скачать

   

   Физика 10 класс. Газовые законыСкачать

   

   Физика фридайвинга. Закон Бойля-Мариотта в действииСкачать

   

   Башня Алхимика-12. Газовые законы. Теория и задачи по законам Бойля-Мариотта, Шарля, Гей-ЛюссакаСкачать