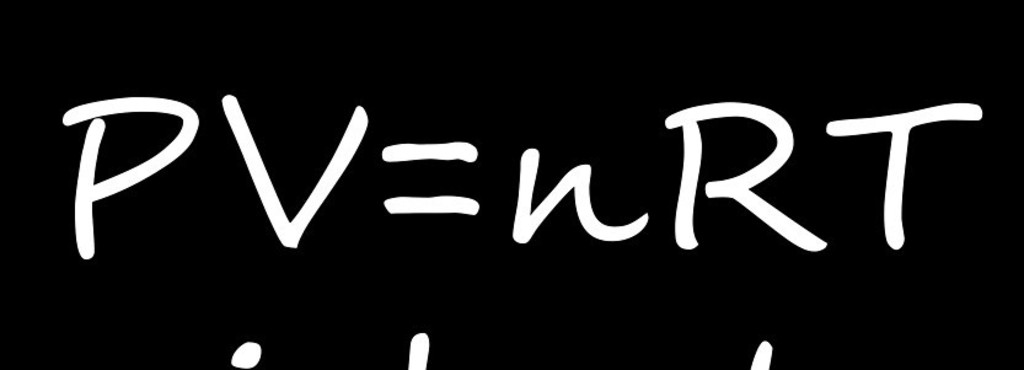Задача на расчет плотности газа с использованием уравнения менделеева клапейрона

Репетитор
по физике

Репетитор
по алгебре

( P ) — Давление газа (Паскали)

( nu ) — Количество вещества

( R ) — Универсальная газовая посиоянная

( T ) — Температура в Кельвинах

В баллоне находится газ под давлением (P= 8,31 cdot 10^6 ; Па ), температура газа (T=300 К ).
Количество вещества газа ( nu=100 Моль ).
Найти объем баллона
Универсальная газовая постоянная ( R=8,31 frac )
Дать ответ в литрах.
Показать ответ Показать решение Видеорешение

Запишем уравнение Менделеева-Клапейрона :

Видео:Относительная плотность газов (D). Определение понятия. Как этим пользоваться при решении задач.Скачать

Алгоритм решения задач на уравнение Менделеева — Клайперона

Разделы: Физика

Алгоритм решения задач на применение уравнения Менделеева – Клайперона.

Многократное (до 7 и более раз) воспроизведение учащимися логически выверенных строго последовательных пошаговых действий дает возможность глубоко и прочно усвоить учебный материал. Представленный алгоритм апробирован. Он позволяет:
1) научить использовать уравнение Менделеева–Клайперона (его варианты);
2) продолжить формирование навыков работы в международной системе единиц “СИ” и культуры оформления решения задач;
3) осуществляет межпредметную связь с алгеброй и химией;
4) воспитывает точность, аккуратность, пунктуальность.

№ шага	Алгоритм	Выполнение
1	Внимательно прочитайте текст задачи.	Баллон содержит 50 л кислорода, температура которого 27° С, а давление 2МПа. Найдите массу кислорода.
2	Запишите в “Дано” буквенное обозначение и числовое значение известных по тексту физических величин. Необходимо знать нормальные условия: р=10 5 Па, t°=0° С	Дано: p=2 МПа
3	Запишите химическую формулу и молярную массу газообразного вещества в “ Дано”, используя систему СИ. М Воздух= 0,029 кг/моль.	О2 М=32•10 –3 кг/моль
4	Под горизонтальной чертой запишите буквенное обозначение неизвестной величины, знак = и?	m= ?
5	Под словом “ Решение” напишите уравнение Менделеева–Клайперона или его вариант:
6	Проделайте алгебраические преобразования так, чтобы по одну сторону знака = стояла неизвестная величина, а по другую – все известные.
7	Проверьте, все ли величины выражены в системе СИ, учитывая, что 1л= 10 –3 м 3 , Т=t° +273 , 1 мм рт. ст.= 133 Па	50 л = 5• 10 –2 м 3 Т = 300 К
8	Подставьте числовые значения вместе с единицами измерения, проведите расчет и работу с единицами измерения, учитывая, что 1 Дж=1 Н? м, 1 Па=1Н/м 2 , 1 Н=1кг? м/с 2
9	Запишите ответ:	Ответ: m=1,3 кг

Задачи для закрепления:

1) Определите массу водорода, находящегося в баллоне емкостью 20 л при давлении 830 кПа, если температура газа равна 17° С.

2) Сосуд вместимостью 40 л содержит 1,98 кг углекислого газа и выдерживает давление не выше 3 МПа. При какой температуре возникает опасность взрыва?

3) Определите плотность азота при нормальных условиях.

4) Какое количество вещества содержится в газе при давлении 200 кПа и температуре 240 К, если его объем 40 л?

5) Какой объем занимает воздух массой 2,9 кг при давлении 750 мм рт.ст. и температуре –3° С?

6) Каково давление азота в сосуде объемом 0,25 м 3 при температуре 32° С? Масса газа 300 г.

Таблицу алгоритма и примеры решения задач на закрепление учитель, исходя из методических потребностей, может размещать как на одной, так и на разных сторонах листа формата А4, раздать ученикам для использования на уроке и дома.

1) 0,014 г;
2) 48° С;
3) 1,23 кг/м 3 ;
4) 4 моль;
5) 2,25 м 3 ;
6) 108624 Па.

Видео:Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Практикум по решению задач на применение уравнения Менделеева-Клапейрона

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

Видеолекции для
профессионалов

• Свидетельства для портфолио
• Вечный доступ за 120 рублей
• 311 видеолекции для каждого

Практикум по решению задач на применение уравнения

Знать физику-означает уметь решать задачи.

Уравнение Менделеева-Клапейрона даёт возможность решить большинство задач на расчёт макропараметров состояния идеального газа

Универсальная газовая постоянная

Молярная масса воздуха 29·10 -3 кг/моль

Ѵ –количество вещества ;

ρ — плотность вещества, ρ

1. Для приведения в движение гребных винтов торпеды применяют воздух, сжатый до 190 ∙ 10 5 Па, в баллонах вместимостью 6 ∙ 10 -1 м 3 . При какой температуре находится воздух, если масса его 130 кг, а молярная масса 29 ∙ 10 -3 кг/моль?

2. Имеется 12 л углекислого газа под давлением 9 ∙ 10 5 Па и при температуре 288 К. Определите массу газа.

3. Какой объем занимает газ в количестве 10 3 моль при давлении 10 6 Па и температуре 100 °С?

4. В сосуде вместимостью 500 см 3 содержится 0,89 г водорода при температуре 17 °С. Определите давление газа.

5. Баллон вместимостью 40 л содержит углекислый газ массой 1,98 кг. Баллон выдерживает давление не выше 3 ∙ 10 6 Па. При какой температуре возникает опасность взрыва?

6. Определите массу водорода, находящегося в баллоне вместимостью 20 л под давлением 830 кПа при температуре 17 °С.

7. Плотность некоторого газообразного вещества равна 1,5 кг/м 3 при 12°С и нормальном атмосферном давлении. Определить молярную массу этого вещества.

8. При нормальных условиях масса газа 738,6 мг, а объем 8,205 л. Какой это газ?

9. Какова плотность гелия при температуре 127 °С и давлении 8,3 ∙ 10 5 Па?

Желаю успеха!

1) 306 К ; 2) 0,2 кг ; 3) 3 м 3 ; 4) 2 МПа; 5) 320 К ; 6) 13,8 гр ; 7) 35·10 -3 кг/моль ; 8) водород ; 9) 1 кг/м 3

Видео:Задачи на уравнение Менделеева-Клапейрона. Ч.1. Краткая теория + решение задачиСкачать

Уравнение Менделеева Клапейрона: формулы для решения задач с газами

Сегодня мы рассмотри уравнение Уравнение Менделеева Клапейрона, которое используется для решения задач по термодинамике.

При решении термодинамических задач по физике, в которых возникают переходы между различными состояниями идеального газа, уравнение Менделеева-Клапейрона является важной опорной точкой. В данной статье рассмотрим, что это за уравнение и как им можно пользоваться при решении практических задач.

Видео:Задачи на уравнение Менделеева-Клапейрона. Ч.2. Решение задач.Скачать

Газы реальные и идеальные

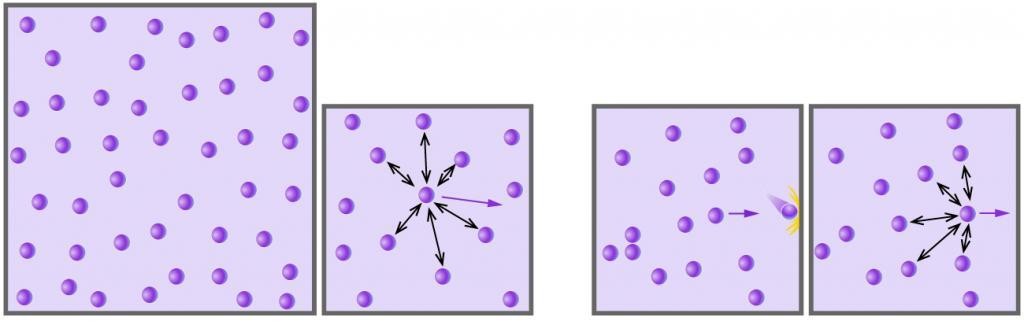
Газовое состояние материи представляет собой одно из существующих четырех агрегатных состояний вещества. Примерами чистых газов являются водород и кислород. Газы могут смешиваться друг с другом в произвольных пропорциях. Всем известный пример смеси — воздух. Названные газы являются реальными, однако при определенных условиях они могут считаться идеальными. Идеальным считается газ, который соответствует следующим характеристикам:

• Частицы, образующие его, не взаимодействуют друг с другом.
• Столкновения между отдельными частицами и между частицами и стенками сосудов носят абсолютно упругий характер, то есть количество движения и кинетическая энергия до и после столкновения сохраняется.
• Частицы не обладают объемом, но имеют некоторую массу.

Все реальные газы при температурах порядка и выше комнатной (больше 300 К) и при давлениях порядка и ниже одной атмосферы (10 5 Па) можно считать идеальными.

Видео:Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать

Описывающие состояние газа термодинамические величины

Под термодинамическими величинами понимают макроскопические физические характеристики, которые однозначно определяют состояние системы. Существует три базовых величины:

Температура отражает интенсивность движения атомов и молекул в газе, то есть она определяет кинетическую энергию частиц. Измеряется эта величина в Кельвинах. Для перевода из градусов Цельсия в Кельвины следует использовать равенство:

Объем — способность каждого реального тела или системы занимать часть пространства. Выражается в СИ в метрах кубических (м 3 ).

Давление — макроскопическая характеристика, которая в среднем описывает интенсивность столкновений частиц газа со стенками сосуда. Чем больше температура и выше концентрация частиц, тем больше будет давление. Выражается оно в паскалях (Па).

Далее будет показано, что уравнение Менделеева-Клапейрона в физике содержит еще один макроскопический параметр — количество вещества n. Под ним полагают число элементарных единиц (молекул, атомов), которое равно числу Авогадро (N_A = 6,02 * 10 23 ). Выражается количество вещества в молях.

Видео:Успеть за 300 секунд, #3: Уравнение Клапейрона-МенделееваСкачать

Уравнение состояния Менделеева-Клапейрона

Запишем сразу это уравнение, а затем объясним его значение. Это уравнение имеет следующий общий вид:

Произведение давления на объем идеального газа является пропорциональным произведению количества вещества в системе на абсолютную температуру. Коэффициент пропорциональности R называется универсальной газовой постоянной. Ее значение равно 8,314 Дж/(моль*К). Физический смысл величины R заключается в том, что она равна работе, которую совершает при расширении 1 моль газа в случае его нагрева на 1 К.

Записанное выражение также называется уравнением состояния идеального газа. Его важность состоит в том, что оно не зависит от химического типа частиц газа. Так, это могут быть молекулы кислорода, атомы гелия или вообще газовая воздушная смесь, для всех этих веществ будет справедливо рассматриваемое уравнение.

Оно может быть записано в других формах. Приведем их:

Здесь m — масса газа, ρ — его плотность, M — молярная масса, N — число частиц в системе, k_B — постоянная Больцмана. В зависимости от условия задачи можно использовать любую форму записи уравнения.

Видео:Урок 2.Уравнение Менделеева-Клапейрона. Решение задач. База. ЕГЭСкачать

Краткая история получения уравнения

Уравнение Клапейрона-Менделеева впервые было получено в 1834 году Эмилем Клапейроном в результате обобщения законов Бойля-Мариотта и Шарля-Гей-Люссака. При этом закон Бойля-Мариотта был известен уже во второй половине XVII века, а закон Шарля-Гей-Люссака впервые был опубликован в начале XIX века. Оба закона описывают поведение закрытой системы при фиксированном одном термодинамическом параметре (температуре или давлении).

Заслуга Д. Менделеева при записи современной формы уравнения идеального газа заключается в том, что он впервые заменил ряд констант одной единственной величиной R.

Отметим, что в настоящее время уравнение Клапейрона-Менделеева может быть получено теоретически, если рассмотреть систему с точки зрения статистической механики и применить положения молекулярно-кинетической теории.

Видео:ТИПОВЫЕ ЗАДАЧИ ПО ХИМИИ: Химическое Количество Вещества, Моль, Молярная Масса и Молярный ОбъемСкачать

Частные случаи уравнения состояния

Существует 4 частных закона, которые следуют из уравнения состояния идеального газа. Остановимся кратко на каждом из них.

Если в закрытой системе с газом поддерживать постоянную температуру, то любое увеличение в ней давления вызовет пропорциональное уменьшение объема. Этот факт может быть записан математически в таком виде:

Этот закон носит фамилии ученых Роберта Бойля и Эдма Мариотта. Графиком функции P(V) является гипербола.

Если в закрытой системе зафиксировать давление, то любое увеличение температуры в ней приведет к пропорциональному возрастанию объема, то есть:

Описанный этим уравнением процесс называется изобарным. Он носит фамилии французских ученых Шарля и Гей-Люссака.

Если в закрытой системе объем не меняется, то процесс перехода между состояниями системы называется изохорным. Во время него любое повышение давления приводит к аналогичному повышению температуры:

Это равенство получило название закона Гей-Люссака.

Графиками изобарного и изохорного процессов являются прямые линии.

Наконец, если зафиксировать макроскопические параметры (температуру и давление), тогда всякое увеличение количества вещества в системе приведет к пропорциональному возрастанию его объема:

Это равенство называется принципом Авогадро. Оно лежит в основе закона Дальтона для идеальных газовых смесей.

Видео:Химия 8 класс (Урок№9 - Относительная плотность газов. Объёмные отношения газов.)Скачать

Решение задачи

Уравнение Менделеева-Клапейрона удобно использовать для решения различных практических задач. Приведем пример одной из них.

Кислород массой 0,3 кг находится в баллоне объемом 0,5 м 3 при температуре 300 К. Как изменится давление газа, если температуру увеличить до 400 К?

Полагая кислород в баллоне идеальным газом, воспользуемся уравнением состояния для вычисления начального давления, имеем:

P₁ = m * R * T₁ / (M * V) = 0,3 * 8,314 * 300 / (32 * 10 -3 * 0,5) = 46766,25 Па.

Теперь вычислим давление, при котором газ будет находиться в баллоне, если поднять температуру до 400 К, получаем:

P₂ = m * R * T₂ / (M * V) = 0,3 * 8,314 * 400 / (32 * 10 -3 * 0,5) = 62355 Па.

Изменение давления при нагреве составит:

Полученное значение ΔP соответствует 0,15 атмосферы.

📺 Видео

Уравнение Менделеева-Клапейрона.Все виды задач на ЕГЭ.52 задачиСкачать

Задачи по химии. Уравнение Менделеева-Клапейрона. Газовые законы. Простейшие химические расчётыСкачать

Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Подготовка к ЕГЭ по ХимииСкачать

Урок 158. Задачи на газовые законы - 1Скачать

Закон Авогадро. Молярный объем. 8 класс.Скачать

Как за 4 МИНУТЫ выучить Химию? Химическое Количество, Моль и Закон АвогадроСкачать

Физика. 10 класс. Решение задач на уравнение Менделеева Клапейрона, часть 1 (2020)Скачать

Решение графических задач на тему Газовые законыСкачать

Решение задач на нахождение молекулярной формулы вещества по известной относительной плотности газаСкачать

Идеальный газ. Уравнение Менделеева-Клапейрона.Скачать