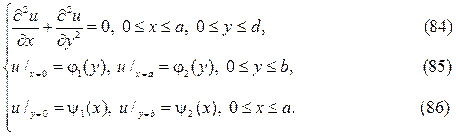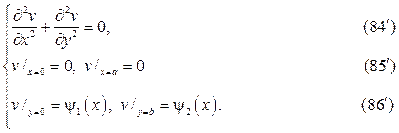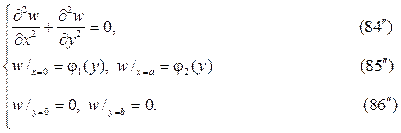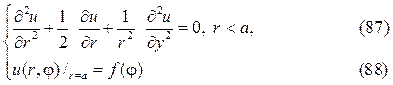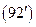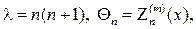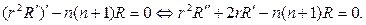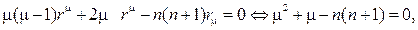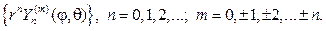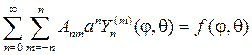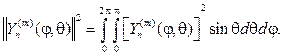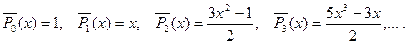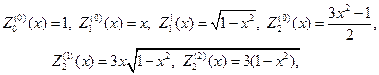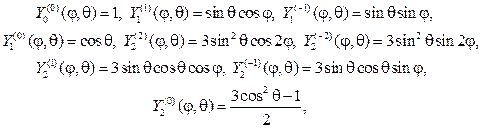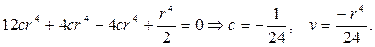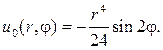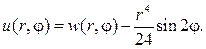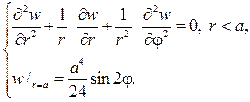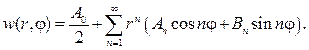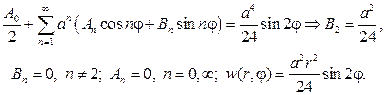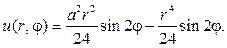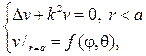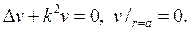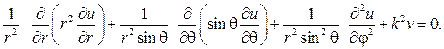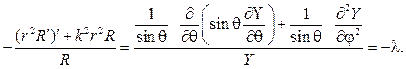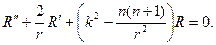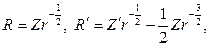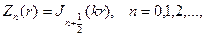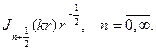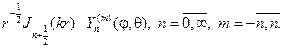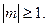ЭЛЛИПТИЧЕСКОГО ТИПА
Краевые задачи для уравнения Лапласа в прямоугольнике (полупо- лосе), решаются методом разделения переменных в декартовых коорди- натах, в круговой областях (круг, сектор, кольцо) методом разделения пе- ременных в полярных координатах. При решении краевых задач для ци-линдрических и сферических областей используются соответственно ци- линдрические и сферические координаты бесселевы функции, полиномы и присоединённые функции Лежандра, а также шаровые функции. Возни- кающие здесь задачи Штурма 
Лиувилля своеобразны, их граничные ус- ловия определяются спецификой областей:
следует искать в виде суммы u(x,y)=v(x,y)+w(x,y),где v(x,y) и w(x,y) гар- монические функции в том же самом треугольнике, точнее они суть ре-шения краевых задач
Штрихованные краевые задачи решаются методом разделения пере- менных в терминах тригонометрических и гиперболических функций.
Рассмотрим задачу Дирихле для круга
где f(j)кусочно-непрерывная функция.
Следуя схеме метода Фурье полагаем
подставляем в (87) и разделяем переменные. В результате получим ра -венство
(90)
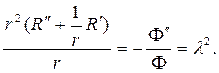
Угловая функция F(j) обязана быть периодической с периодом 2p. Присоединяя условие периодичности к дифференциальному уравнению для F(j), найдем задачу Штурма Лиувилля
откуда следует, что
(91)
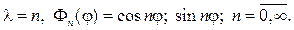
Возвращаясь к (80), решаем уравнение для радианальной функции. При
r 2 R² + rR¢ n 2 R = 0,
решение следует искать в виде степенной функции R=r m . Для определе- ния m получим соотношение
m(m 1)r m +m r m 
n 2 r m =0Û m 2 
n 2 =0,
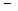
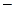
Если же n=0, то уравнение, как нетрудно проверить, rR² + R¢ =0имеет своими решениями функции
R0(r) = 1; lnr. 
С учетом (89) мы должны составить произведения угловых и радиаль- ных функций и получить набор функций, гармонических в круге
Если предположить, что ряд
(93)
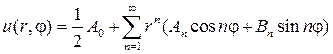
можно дифференцировать почленно дважды по r и j , то его сумма также будет гармонической функцией, т. е. будет решением уравнения (87). Подставляя (93) в (88), найдем
(94)
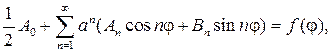
откуда с учетом формул коэффициентов Фурье следует
(95)
(96) Итог состоит в том, что решение задачи (87 88) дается рядом (93), коэффициенты которого определены равенствами (95-96).
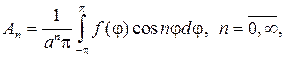
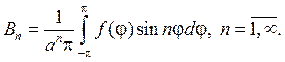
Замечание 1. Мы можем говорить, очевидно, что ряд (93) дает общий вид гармонической функции для круга r — n и lnr, поскольку они разрывны в
центре круга r=0.
Напротив, если рассматривать область r>a, то нельзя привлекать r — n и lnr, и общий вид гармонической функции для внешности круга будет да- ваться рядом
(97)
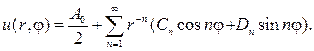
В случае кругового кольца a 2 q= 1-x 2 , найдем
(104¢)
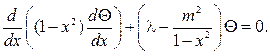
Соответственно и граничные условия (105) перейдут после замены в неравенства
(105′)
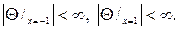
Задача (104¢) (105¢) есть известная задача для присоединенных функций Лежандра, ее решение (см., например, [3], стр. 115)
и возвращаясь к переменной q, найдем собственные значения и собствен- ные функции задачи (104), (105):
(106)
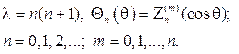
Составив произведения функций (106) на найденные выше функции Fm(j), получим множество решений уравнения (102)
(107)
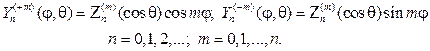
Эти решения принято называть сферическими функциями, их основ-ное свойство в приводимой ниже теореме.
Теорема 1. Сферические функции взаимно ортогональны на единич- ной сфере, т.е. при m1¹m2 или n1¹n2
(108)
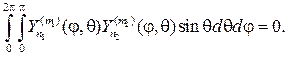
Теперь возвращаясь к равенству (101), возьмем уравнение для ради- альной функции
Оно имеет решение в виде степенной функции R=r m . Действительно, после подстановки
откуда находим значения m=n; (n+1) и соответственно решения
(109)
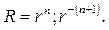
Умножая первые из функций (109) на сферические функции (107), получаем множество частных решений уравнения Лапласа в шаре:
Согласно схеме метода Фурье. составляем ряд с произвольными коэффи- циентами
(110)
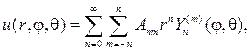
который будет гармонической функцией в шаре, если только его можно дифференцировать почленно.
Для нахождения коэффициентов Аnm подставим (110) в (100), тогда
и с учетом (108) найдем
(111)
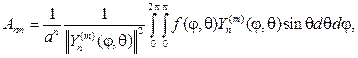
Последний интеграл вычисляется и при m=0 :
(112)
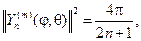
если же |m| ³ 1, то имеем
(113)
Завершая рассмотрение задачи (99),(100), скажем, что мы нашли ее решение в виде ряда (110), коэффициенты которого определяются в согласии с (111),(113).
Замечание 3. Напомним, что нормированные полиномы Лежандра вы- числяяются по формулам
(114)
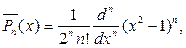
В свою очередь присоединенные функции Лежандра выражаются че- рез производные от полиномов Лежандра, т. е.
(115)
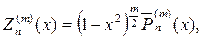
в частности будем иметь
(116)
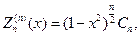
где Сn определенная константа.
С учетом (107), (115) и (116) выпишем несколько сферических функций:
(117)
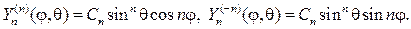
Замечание 4. При решении краевых задач для внешности шара вместо соотношения (110) нужно использовать ряд
(118)
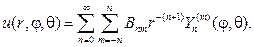
Общий вид гармонической функции в шаровом слое a 4 , и получим
Таким образом, частным решением будет функция
Вводим новую неизвестную функцию w(r,j) , полагая
Тогда относительно w(r,j) нужно решать задачу Дирихле для урав- нения Лапласа
Согласно (93), решение этой задачи дается формулой
Подставляя ее в граничное условие, получим
Ответом в задаче будет функция
254. Найдите решение первой краевой задачи для уравнения Гельмгольца
предполагая, что k не является собственным значением задачи
Р е ш е н и е. Запишем уравнение в сферических координатах
Беря u(r,j,q,)=R(r)Y(j,q), после разделения переменных придем к дифференциальным уравнениям:
Функция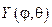 
будет решением уравнения (72), которое нужно решать при условии ограниченности и 2p-периодичности по j. В результате при- дем к сферическим функциям при l=n(n+1):
Относительно радиальной функции R(r) нужно решать дифференци- альное уравнение
Выполняя в этом уравнении замену
придем к соотношению относительно новой функции Z(r):
Последнее уравнение в качестве ограниченных в окрестности нуля
r=0 решений имеет бесселевы функции
соответственно будем иметь набор радиальных функций
Умножая их на сферические функции, получим набор решений урав- нения Гельмгольца:
Составляем ряд с числовыми коэффициентами
(119)
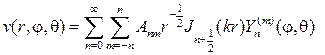
и определяем коэффициенты так, чтобы выполнялась граничное условие при r=a
где d = 4 при m = 0 и d =2 при 
При найденных коэффициентах Anm ряд (119) будет решением рассматриваемой краевой задачи для уравнения Гельмгольца.
255. Найдите такую гармоническую u(r,j,q) функцию внутри шарового слоя 1
Видео:Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать
Решение задачи Дирихле для круга методом разделении переменных
На плоскости R 2 с координатами х, у рассмотрим круг Q радиуса R, описанный вокруг начала координат О. Граница круга — окружность где g(P) — заданная функция на окружности Г. Требуется найти решение HeC 2 (Q)nC(o).
Г = 8Q (см. рис 12.2). Для круга сформулируем внутреннюю задачу Дирихле для уравнения Лапласа:
В полярных координатах р, , , отделяя функции, зависящие
от р и функции зависящие от (р, тогда
Выражение слева зависит только от р, а выражение справа — только от (р, поэтому равенство имеет место тогда и только тогда, когда эти выражения являются постоянными величинами, то сеть
где р — постоянная разделения.
В результате получим два обыкновенных дифференциальных уравнения:
Рассмотрим случай, когда р* 0. Общие решения уравнений (12.18) определяются формулами
Рассмотрим случай, когда ц = 0. Уравнения (12.18) примут вид
Запишем общие решения этих уравнений:
После подстановки функций (12.19), (12.20) в (12.17) получим частные решения уравнения Лапласа в полярных координатах:
По смыслу задачи (12.15), (12.16) решение и должно быть периодическим по углу (р с периодом 2л — , то есть и(р, ). Условие периодичности для функций (12.21) будет выполнено, если Д, = 0, // = п = 1,2.
В результате получим последовательность частных периодических решений уравнения (12.15):
Образуем общее решение уравнения (12.15) в виде линейной комбинации частных решений (12.22):
По смыслу задачи решение и должно быть ограниченным в центре круга р = 0. В связи с этим необходимо положить С0 = 0, Dn = 0.
Видео:6.2 Решение задач для уравнения Лапласа в круге, вне круга и в кольцеСкачать
Основные понятия метода сеток. Задача Дирихле для уравнения Лапласа
Метод сеток (или метод конечных разностей) сводит решение систем уравнений в частных производных к решению систем линейных, как правило, алгебраических уравнений с достаточно разреженными матрицами. При этом построение решения в методе сеток осуществляется в три этапа.
- • Область непрерывного изменения аргумента (или аргументов) заменяется конечным дискретным множеством точек, называемых разностной сеткой. В разностной сетке выделяются внутренние и граничные узлы. Решение ищется во внутренних узлах, а в граничных узлах значение искомой функции задается при аппроксимации граничных условий исходной дифференциальной задачи. Функция дискретного аргумента, определенная на разностной сетке, называется СЕТОЧНОЙ ФУНКЦИЕЙ.
- • Дифференциальное уравнение и граничные условия заменяются по определенным правилам своими разностными аналогами. Разностные операторы, соответствующие дифференциальному уравнению, записываются во внутренних узлах сетки. Разностные операторы, соответствующие граничным условиям, записываются в граничных узлах. В результате получается система алгебраических уравнений, число которых пропорционально числу внутренних узлов разностной сетки.
- • Осуществляется решение системы алгебраических уравнений каким-либо из известных методов. В большинстве случаев получаемая система уравнений есть система линейных алгебраических уравнений достаточно большого порядка, но с весьма разреженной матрицей. В случае нелинейных систем итерационные процедуры, как правило, сводят их к линейным системам.
Основные понятия и этапы метода сеток продемонстрируем на примере решения задачи Дирихле для классического уравнения эллиптического типа — уравнения Лапласа. Итак, имеем уравнение Лапласа
и граничное условие 
где Г — граница области G (рис. 4.4), в которой ищется решение и(х, у), удовлетворяющее уравнению (4.7) и граничному условию (4.8).
На первом этапе метода сеток область G непрерывного изменения аргумента с границей Г заменяют приближающей ее сеточной областью Gh с границей Г’А. Для этого проведем линии
при п = 0, . N. Величины hx и h , называемые шагами разностной сетки, в общем случае могут быть различными.
Рис. 4.4 Рис. 4.5
Точки пересечения линий х = const и у = const называют УЗЛАМИ РАЗНОСТНОЙ СЕТКИ. Различают два типа узлов — ВНУТРЕННИЕ и ВНЕШНИЕ. Внутренними называют такие узлы, для которых четыре соседних узла (по два в каждом направлении) принадлежат области G = G + Г. Сеточной функции приписываются нижние индексы. На рис. 4.4 внутренние узлы обозначены пустыми кружочками, а граничные — залитыми.
На втором этапе заменим дифференциальный оператор Лапласа разностным оператором. С этой целью выберем шаблон разностной схемы — набор (конфигурацию) узлов, с использованием которых производится замена производных конечными разностями. Шаблон, содержащий р точек, называется р-точечным. Для аппроксимации вторых производных, входящих в оператор Лапласа, применим пятиточечный шаблон, показанный на рис. 4.5. Не теряя общности рассуждений, рассмотрим далее случай, когда шаги разностной сетки по направлению х иу одинаковы, т. е. hx — hy = h. С использованием разложения функции на точном решении в ряд Тейлора в окрестности точки (*, у) имеем
Из этих соотношений получим аппроксимации вторых производных со вторым порядком точности
Введем для сокращения записи общепринятые индексные обозначения узлов в соответствии с рис. 4.5 и соответствующие обозначения сеточных функций в узлах: ит ит. „ и т. д. Тогда соотношения для производных примут вид
При этом разностный оператор Лапласа Дuh на пятиточечном шаблоне может быть выписан как
Аппроксимация граничных условий осуществляется с помощью различных приемов. Для случая прямоугольной области с границами, совпадающими с линиями х — const и у — const, граничные значения известны в узлах точно, так как и0 h = = uQ(mhx, nhy). Для области произвольной формы значения сеточной функции в граничных узлах принимаются равными значениям функции и0 в ближайших (по какому-либо критерию) точках кривой Г (рис. 4.4). Для задачи Неймана или смешанной задачи, когда на границе области задается значение производной функции и, производится аппроксимация производной.
Записав разностный оператор (4.11) во всех внутренних узлах, получим систему сеточных уравнений для нахождения значений сеточной функции ит п в узлах разностной сетки.
На третьем этапе осуществляется решение системы сеточных уравнений. В общем случае сеточные уравнения могут быть нелинейными. Однако в рассматриваемой задаче, в силу линейности основного дифференциального уравнения Лапласа, система уравнений (4.11) является системой линейных алгебраических уравнений для нахождения значений неизвестных во внутренних узлах. При этом число уравнений системы точно равно числу внутренних узлов разностной сетки. Отметим, что число уравнений может быть весьма велико. Так, для нахождения достаточно точного решения рассматриваемой задачи требуется задать числа N = М порядка 50—100, и, следовательно, количество уравнений достигает нескольких сотен или даже тысяч.
Перепишем систему сеточных решений в виде
Отметим, что каждое из уравнений системы содержит лишь пять неизвестных ит , . „, и„ , „ . ,, ит „ ., и„ хотя в полной
системе таких неизвестных содержится порядка N 2 . Таким обра- зом, матрица системы (4.12) является сильно разреженной. Системы с такими матрицами хорошо решаются с помощью итерационных методов: простой итерации, Зейделя, релаксационных. Рассмотрим их применение к решению системы (4.12).
Запишем систему (4.12) в виде
Значение функции в центральной точке есть среднее арифметическое значений функции в четырех соседних по направлениям х и у узлах. Уравнение (4.13) можно интерпретировать как разностный аналог теоремы о среднем для гармонических функций.
Рассмотрим применение метода простой итерации для решения системы (4.13). Для простоты предположим, что область G имеет прямоугольную форму (рис. 4.6). Построим итерационный процесс
Здесь верхний индекс означает номер итерации. В граничных точках значения известны точно. Для нахождения решения по соотношению (4.14) необходимо знать начальное приближение — значения функции на нулевой итерации ц ( ®* п. Можно доказать, что для любого шага разностной сетки итерационный процесс (4.14) сходится независимо от начального приближения и п. На практике желательно выбирать начальное приближение возможно более близким к точному решению. Например, на основании теоремы о среднем для гармонических функций в качестве хорошего начального приближения можно принять значение функции, полученное интерполяцией на область G значений
функции в граничных узлах. Так, значение функции и (0) в центральной точке 1 (рис. 4.6) может быть взято как среднее арифметическое значений функции в граничных узлах a, b, с, d.
Сходимость итерационного процесса можно улучшить, если использовать итерационный процесс Зейделя в виде, например,
Члены с индексами (т — 1, п) и (т, п — 1) берутся из k-й итерации, т. е. в вычислениях используются уточненные значения функции в этих точках. Как легко понять из рис. 4.6, расчет по формуле (4.15) при движении, например, слева направо от границы области позволяет последовательно вычислить значения функции на слоях у = const (или х = const). Использование уточненных значений функции улучшает сходимость метода итераций и позволяет уменьшить требуемый для реализации метода объем оперативной памяти компьютера, так как в методе Зейделя не требуется одновременно хранить значение функции в каждой точке на двух итерациях. Итерации заканчиваются при выполнении условия max |u^ — ” **1 1 итерационный метод называется методом ВЕРХНЕЙ РЕЛАКСАЦИИ, при со = 1 — методом ПОЛНОЙ РЕЛАКСАЦИИ и при со 2 ]пе-‘
Метод итераций Зейделя
Метод верхней релаксации
Видно, что в методе верхней релаксации число итераций для достижения заданной точности линейно зависит от числа узлов N, тогда как в остальных методах зависимость квадратичная.
🔥 Видео
Задача Дирихле для круга. Уравнение ЛапласаСкачать
7.1 Решение уравнения Лапласа в прямоугольникеСкачать
Методы математической физики. Задача Дирихле для уравнения Лапласа в круге. 19.05.21 Фролова Е.В.Скачать
Метод Фурье для неоднородного уравнения теплопроводностиСкачать
OTAROVA JAMILA МЕТОД ФУРЬЕ РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В ПРЯМОУГОЛЬНОЙСкачать
OTAROVA JAMILA МЕТОД ФУРЬЕ РЕШЕНИЯ ЗАДАЧИ ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕСкачать
Метод разделения переменных - 2Скачать
Колыбасова В.В. - Методы математической физики. Семинары - 7.Внешняя краевая задача для ур.Лапласа 2Скачать
Радкевич Е.В. - Уравнения математической физики - 6.Задача Неймана для уравнения ЛапласаСкачать
Задача Дирихле для уравнения Лапласа в кольце и сектореСкачать
Уравнение Лапласа. Задача Дирихле для уравнения Лапласа внутри и вне кругаСкачать
6-2. Метод сетокСкачать
5. Решение волнового уравнения на отрезке методом ФурьеСкачать
Метод разделения переменных - 1Скачать
Радкевич Е.В. - Уравнения математической физики - 7. Примеры метода ФурьеСкачать
Уравнения математической физики 15+16 Задача Дирихле для уравнения Лапласа - Пуассона в кругеСкачать
