Зачем нужны уравнения в жизни (4 видео)

ru.mosg-portal.com

Как используются линейные уравнения в повседневной жизни? — Наука

Содержание

Содержание:
Различные цены
Ставки
составление бюджета
Делать прогнозы
Зачем нужны уравнения в жизни
Применение квадратных уравнений в жизни
Просмотр содержимого документа «Применение квадратных уравнений в жизни»
🔥 Видео

Видео:Математика не нужна!Скачать

Содержание:

Линейные уравнения используют одну или несколько переменных, где одна переменная зависит от другой. Практически любая ситуация, когда существует неизвестное количество, может быть представлена линейным уравнением, например, вычисление дохода с течением времени, расчет скорости пробега или прогнозирование прибыли. Многие люди используют линейные уравнения каждый день, даже если они делают вычисления в своей голове, не рисуя линейный график.

Видео:Наглядно показываю, зачем нужны логарифмы в жизниСкачать

Различные цены

Представьте, что вы едете на такси во время отпуска. Вы знаете, что служба такси берет 9 долларов, чтобы забрать вашу семью из отеля, и еще 0,15 доллара за милю за поездку. Не зная, сколько миль будет до каждого пункта назначения, вы можете установить линейное уравнение, которое можно использовать для определения стоимости любой поездки на такси, которую вы совершаете в своей поездке. Используя «x» для представления количества миль до пункта назначения и «y» для представления стоимости поездки на такси, линейное уравнение будет иметь вид: y = 0,15x + 9.

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Ставки

Линейные уравнения могут быть полезным инструментом для сравнения ставок заработной платы. Например, если одна компания предлагает платить вам 450 долларов в неделю, а другая предлагает 10 долларов в час, и обе просят вас работать 40 часов в неделю, какая компания предлагает лучшую ставку оплаты? Линейное уравнение может помочь вам понять это! Первое предложение компании выражается как 450 = 40x. Предложение второй компании выражается как y = 10 (40). После сравнения двух предложений уравнения показывают, что первая компания предлагает лучшую ставку оплаты в 11,25 долл. В час.

Видео:#200. ЗАЧЕМ НУЖНА МАТЕМАТИКА?Скачать

составление бюджета

Планировщик вечеринок имеет ограниченный бюджет на предстоящее мероприятие. Шелл нужно выяснить, сколько будет стоить ее клиенту арендовать помещение и платить за еду на человека. Если стоимость аренды помещения составляет 780 долл. США, а цена на человека на продукты питания составляет 9,75 долл. США, можно построить линейное уравнение, чтобы показать общую стоимость, выраженную в виде у, для любого количества присутствующих людей, или х. Линейное уравнение будет записано в виде y = 9,75x + 780. С помощью этого уравнения планировщик вечеринок может заменить любое количество гостей вечеринки и предоставить ее клиенту фактическую стоимость мероприятия с учетом расходов на питание и аренду.

Видео:ЗАЧЕМ НУЖНЫ ЭТИ ... логарифмы! Математика на QWERTYСкачать

Делать прогнозы

Одним из наиболее полезных способов применения линейных уравнений в повседневной жизни является прогнозирование того, что произойдет в будущем. Если комитет по продаже выпечки тратит 200 долл. США на первоначальные начальные затраты, а затем зарабатывает 150 долл. США в месяц на продажах, линейное уравнение y = 150x — 200 можно использовать для прогнозирования совокупной прибыли от месяца к месяцу. Например, через шесть месяцев комитет может рассчитывать получить 700 долларов, потому что (150 x 6) — 200 = 700 долларов. Хотя факторы реального мира, безусловно, влияют на точность прогнозов, они могут быть хорошим показателем того, чего ожидать в будущем. Линейные уравнения являются инструментом, который делает это возможным.

Видео:Зачем нужны квадратные уравнения?Скачать

Зачем нужны уравнения в жизни

Вот пример прямой задачи: сколько весит кусок сплава, на изготовление которого пошло 0,6 дм³ меди (уд. вес 8,9 кг / дм³) и 0,4 дм³ цинка (уд. вес 7,0 кг/ дм³)? При ее решении мы находим вес взятой меди (8,9 · 0,6 = 5,34 (кг)), затем вес цинка (7,0 · 0,4 = 2,8 (кг)) и, наконец, вес сплава (5,34 + 2,8 = 8,14 (кг)). Выполняемые действия и их последовательность диктуются самим условием задачи.

Вот пример косвенной задачи: кусок сплава меди и цинка объемом в 1 дм³ весит 8,14 кг. Найти объемные количества меди и цинка в этом сплаве. Здесь из условия задачи не видно, какие действия ведут к ее решению. При так называемом арифметическом решении нужно проявить подчас большую изобретательность, чтобы наметить план решения косвенной задачи. Каждая новая задача требует создания нового плана. Труд вычислителя затрачивается нерационально. Для рационализации вычислительного процесса и был создан метод уравнений, который является основным предметом изучения в алгебре. Суть этого метода такова.

1.Искомые величины получают особые наименования. Мы пользуемся для этой цели буквенными знаками (предпочтительно последними буквами латинского алфавита х, у, z, u, v). Условие задачи с помощью этих знаков и знаков действий (+, — и т. д.) «переводится на математический язык», т. е. связи между данными и искомыми величинами мы выражаем не словами и фразами разговорного языка, а математическими знаками. Каждая такая «математическая фраза» и есть уравнение.

2.После этого мы решаем уравнение, т. е. находим значения искомых неизвестных величин. Решение уравнения производится совершенно механически, по общим правилам. Нам не приходится больше учитывать особенности данной задачи; мы только должны применять раз навсегда установленные правила и приемы. (Выводом этих правил и занимается в первую очередь алгебра.)

Таким образом, уравнения нужны для того, чтобы механизировать труд вычислителя. После того как уравнение составлено, решение его можно получить вполне автоматически (в настоящее время сконструирован ряд таких автоматов). Вся трудность решения задачи сводится лишь к составлению уравнения.

Видео:Уравнение, которое меняет взгляд на мир [Veritasium]Скачать

Применение квадратных уравнений в жизни

Презентация к открытому уроку по алгебре в 8 классе по теме » Квадратные уравнения»

Просмотр содержимого документа
«Применение квадратных уравнений в жизни»

«Квадратные уравнения в жизни»

Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Умение решать уравнения не только имеет теоретическое значение для познания естественных законов, но и служит практическим целям.

Важность умения решать квадратные уравнения в очередной раз доказывает то, что такие уравнения умели решать еще в древности. Но как это делалось, если в то время не существовала символическая алгебра?

История возникновения и развития квадратных уравнений

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.

Квадратные уравнения решали еще в Индии. Древнеиндийский математик Баудхаяма. впервые использовал квадратные уравнения в форме ax2= c и ax2+ bx = c и привел методы их решения.

Формулы решения квадратных уравнений в Европе были впервые изложены в 1202 г. в «Книге абака» итальянским математиком Леонардом Фибоначчи.

Далее квадратные уравнения продолжают изучать и другие выдающиеся математики

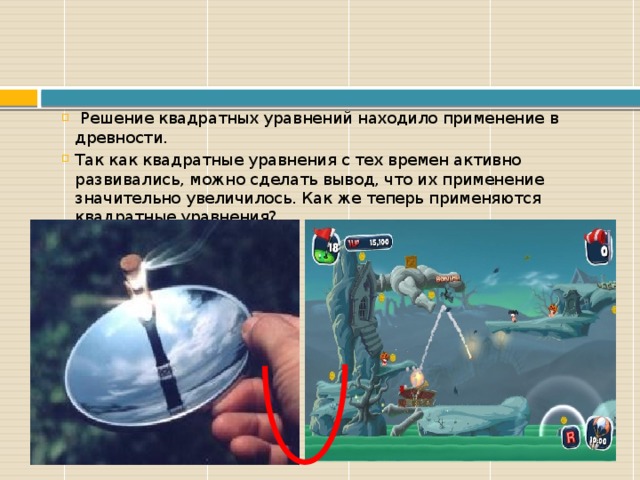
Решение квадратных уравнений находило применение в древности.
Так как квадратные уравнения с тех времен активно развивались, можно сделать вывод, что их применение значительно увеличилось. Как же теперь применяются квадратные уравнения?

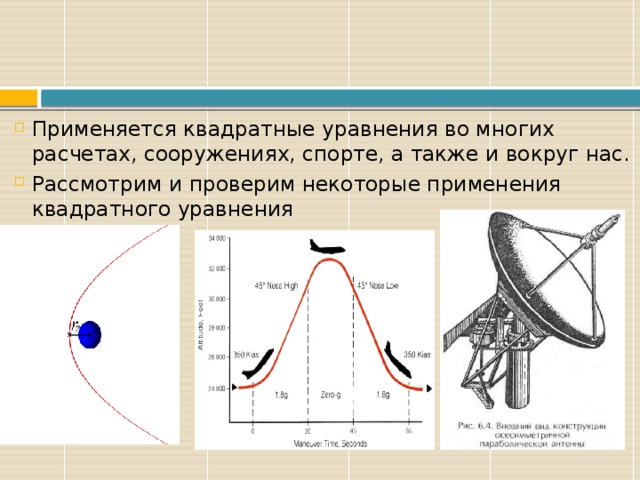
Применяется квадратные уравнения во многих расчетах, сооружениях, спорте, а также и вокруг нас.
Рассмотрим и проверим некоторые применения квадратного уравнения

Сейчас ученые выяснили, что траекторию движения планет можно найти с помощью квадратного уравнения.

Взлет главная составляющая полета. Здесь берется расчет для маленького сопротивления и ускоренного взлета.

Фонтан смотрится лучше, если капли воды достигают высоты, большей, чем высота статуи.

В данном виде спорта, крайне важны арифметические расчеты.

При разбеге прыгуна в высоту для максимально четкого попадания на планку отталкивания и высокого полета, используют расчеты связанные с парабалой.

Также подобные расчеты нужны в метании. Дальность полета объекта зависит от квадратного уравнения.

Квадратные уравнения получили большое значение и значительное применение в жизни.

Квадратное уравнение имеет большое применение в жизни. Еще в древности человек использовал квадратное уравнение. А с тех пор применение квадратного уравнения только росло.

Проходя эту тему на уроке, мы мало задумываемся о практическом применении квадратных уравнений. Поэтому мы считаем, что квадратные уравнения нигде не используются, но как выяснилось это не так.