Зачем нужны линейные уравнения в жизни (2 видео)

Применение линейной функции в жизни человека

презентация исследования линейной функции в жизни

Содержание

Скачать:
Подписи к слайдам:
ru.mosg-portal.com
Содержание:
Различные цены
Ставки
составление бюджета
Делать прогнозы
Нпк «Линейная функция в жизни человека»
Просмотр содержимого документа «Нпк «Линейная функция в жизни человека»»
🎬 Видео

Видео:Что такое линейная алгебра, зачем нужна и как с ней работать? Душкин объяснитСкачать

Скачать:

Вложение	Размер
lineynaya_funktsiya.ppt	1.87 МБ

Предварительный просмотр:

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Подписи к слайдам:

Научная исследовательская работа по прикладной математике Тема: Применение линейной функции в жизни человека.

Цель и задачи исследования Цель исследования- поиск задач на применение линейной функции в жизни человека. Задачи исследования: 1) Изучение научной литературы по данной теме. 2) Решение задач по теме, оценка полученных результатов.

Актуальность выбранной темы Изучение линейной функции является актуальной всегда, т.к. с помощью неё описываются реальные процессы происходящие в природе на языке математики. С помощью линейной функции можно описать процессы движения, изменения присущие природе.

Функция вида у = к х + m называется линейной, где к, m – числа (коэффициенты), х – независимая переменная(или аргумент), у – зависимая переменная( или функция) Свойства: D(f)= (-∞; +∞); E(f)= (-∞; +∞); Возрастает, если k>0, убывает, если k 0, у>0 и к >0, то зависимость между переменными х, у , выражаемую формулой у = к х, называют прямой пропорциональной зависимостью, а число к –коэффициентом пропорциональности. Цена р купленного отреза ткани пропорциональна его длине l, а именно p=kl ,где k – цена одного метра ткани Таблица прироста вклада в сберегательном банке в зависимости от суммы вклада Стоимость товара купленного по одной цене пропорциональна его количеству Производство продукции и расход материала

Содержание другого вида продукта в данном виде продукта пропорционально количеству продукта Содержание сахара в сахарной свёкле пропорционально количеству сахарной свёклы Содержание крахмала в картофеле прямо пропорционально количеству картофеля Содержание подсолнечного масла пропорционально количеству семян подсолнечника Количество яблочного пюре прямо пропорционально количеству яблок

Многие физические законы выражаются с помощью прямой пропорциональной зависимости Напряжение U по закону Ома линейно зависит от силы тока Y , именно Y= RU ,где R –сопротивление. Этот закон справедлив при не очень больших изменения силы тока. Масса воды и льда прямо пропорциональна его объёму

Заключение Для выполнения цели исследования были подобранны задачи из различных областей жизни человека: физики, экономики, в банковском деле, торговле и т.д. Работа будет интересна преподавателям, ученикам, студентам т.е. любителям математики. Возможно продолжение работы: применение квадратичной, степенной, показательной, логарифмической, тригонометрических функций и т. д. в жизни человека.

Список литературы 1 Алимов Ш.А., Колягин Ю.М , Сидоров Ю.В. и др. Алгебра: учебник для 7 класса общеобразовательных учреждений М. : Просвещение, 2002. – 207с. 2 Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др. Алгебра: учебник для 9 класса общеобразовательных учреждений М. : Просвещение ,2002. – 255с. 3 Величко М.В. авт.-сост. Математика. 9-11 классы: проектная деятельность учащихся Волгоград: Учитель,2007.-123с. 4 Звавич Л.И., Кузнецова Л.В., Суворова С.Б. Дидактические материалы по алгебре 7 класс. М.: Просвещение 2003 – 158с. 5 Матвиевская Г.П. Рене Декарт М.: Просвещение 1987 — 79с. 6 Мордкович А.Г. Алгебра 7 класс. Часть1.Учебник для учащихся общеобразовательных учреждений М.:Мнемозина,2009.- 160с. 7 Мордкович А.Г. и др. Алгебра 7 класс. Часть2.Задачник для учащихся общеобразовательных учреждений М.:Мнемозина,2009.- 223с. 8 Мордкович А.Г. и др. Алгебра 9 класс. Часть1.Учебник для учащихся общеобразовательных учреждений М.:Мнемозина,2010.- 224с. 10 Музенитов Ш. Функциональные зависимости с экономическим содержанием. Журнал Математика – ноябрь 2011г – с.22 – 24 11 Никольская И.Л. составитель Факультативный курс по математике. Учебное пособие для 7 – 9 классов средней школы М.: Просвещение, 1991,-383с. 12 Симонов А.С. Проценты и банковские расчёты. Журнал Математика в школе – июль- август 1998г,- с.37-44

Видео:Линейное уравнение. Что это?Скачать

ru.mosg-portal.com

Как используются линейные уравнения в повседневной жизни? — Наука

Видео:Для чего матрицы в жизни? | Высшая математика | TutorOnlineСкачать

Содержание:

Линейные уравнения используют одну или несколько переменных, где одна переменная зависит от другой. Практически любая ситуация, когда существует неизвестное количество, может быть представлена линейным уравнением, например, вычисление дохода с течением времени, расчет скорости пробега или прогнозирование прибыли. Многие люди используют линейные уравнения каждый день, даже если они делают вычисления в своей голове, не рисуя линейный график.

Видео:Уравнение, которое меняет взгляд на мир [Veritasium]Скачать

Различные цены

Представьте, что вы едете на такси во время отпуска. Вы знаете, что служба такси берет 9 долларов, чтобы забрать вашу семью из отеля, и еще 0,15 доллара за милю за поездку. Не зная, сколько миль будет до каждого пункта назначения, вы можете установить линейное уравнение, которое можно использовать для определения стоимости любой поездки на такси, которую вы совершаете в своей поездке. Используя «x» для представления количества миль до пункта назначения и «y» для представления стоимости поездки на такси, линейное уравнение будет иметь вид: y = 0,15x + 9.

Видео:Математика не нужна!Скачать

Ставки

Линейные уравнения могут быть полезным инструментом для сравнения ставок заработной платы. Например, если одна компания предлагает платить вам 450 долларов в неделю, а другая предлагает 10 долларов в час, и обе просят вас работать 40 часов в неделю, какая компания предлагает лучшую ставку оплаты? Линейное уравнение может помочь вам понять это! Первое предложение компании выражается как 450 = 40x. Предложение второй компании выражается как y = 10 (40). После сравнения двух предложений уравнения показывают, что первая компания предлагает лучшую ставку оплаты в 11,25 долл. В час.

Видео:Математика это не ИсламСкачать

составление бюджета

Планировщик вечеринок имеет ограниченный бюджет на предстоящее мероприятие. Шелл нужно выяснить, сколько будет стоить ее клиенту арендовать помещение и платить за еду на человека. Если стоимость аренды помещения составляет 780 долл. США, а цена на человека на продукты питания составляет 9,75 долл. США, можно построить линейное уравнение, чтобы показать общую стоимость, выраженную в виде у, для любого количества присутствующих людей, или х. Линейное уравнение будет записано в виде y = 9,75x + 780. С помощью этого уравнения планировщик вечеринок может заменить любое количество гостей вечеринки и предоставить ее клиенту фактическую стоимость мероприятия с учетом расходов на питание и аренду.

Видео:Пример использования высшей математики в жизни человека - обогрев крышиСкачать

Делать прогнозы

Одним из наиболее полезных способов применения линейных уравнений в повседневной жизни является прогнозирование того, что произойдет в будущем. Если комитет по продаже выпечки тратит 200 долл. США на первоначальные начальные затраты, а затем зарабатывает 150 долл. США в месяц на продажах, линейное уравнение y = 150x — 200 можно использовать для прогнозирования совокупной прибыли от месяца к месяцу. Например, через шесть месяцев комитет может рассчитывать получить 700 долларов, потому что (150 x 6) — 200 = 700 долларов. Хотя факторы реального мира, безусловно, влияют на точность прогнозов, они могут быть хорошим показателем того, чего ожидать в будущем. Линейные уравнения являются инструментом, который делает это возможным.

Видео:КАК РАЗОБРАТЬСЯ В ВЫСШЕЙ МАТЕМАТИКЕСкачать

Нпк «Линейная функция в жизни человека»

Данная работа содержит результаты исследования, поиска и решения прикладных задач, в которых зависимость переменных выражается линейной функцией.

Просмотр содержимого документа
«Нпк «Линейная функция в жизни человека»»

На сегодняшний день тема «Применение математических функций в жизни человека и различных науках» является актуальной и интересной. Впервые об этой теме я услышал на уроке математики, познакомившись с понятием линейная функция. Мне стало интересно: с какими реальными ситуациями связано понятие «линейная функция», т.е. между какими величинами можно установить линейные зависимости? Каким образом устанавливается зависимость между величинами? Как установленную зависимость можно записать, или изобразить и каким образом использовать установленные зависимости? Моя исследовательская работа посвящена изучению практического применения линейной функции в науке, жизни. В повседневной жизни мы очень часто используем линейную функцию, составляющую основу математики. Данная работа содержит результаты исследования, поиска и решения прикладных задач, в которых зависимость переменных выражена линейной функцией. Реальные процессы обычно связаны с большим количеством переменных и зависимостей между ними. Описать эти зависимости можно с помощью функций. Знание свойств функций позволяет понять суть происходящих процессов, предсказать ход их развития, управлять ими. Изучение функций является актуальным всегда.

Проблемный вопрос: линейная функция факт или теория?

Гипотеза: я предположил, что в окружающем мире есть величины, которые связаны между собой линейными зависимостями.

Цель: увидеть связь линейной функции с явлениями окружающего мира и практической деятельностью человека, показать, что понятие “линейная функция” находит широкое применение в жизни.

подобрать и проанализировать соответствующую литературу и интернет — источники;

найти определение функции в школьной программе;

рассмотреть применение функции в различных науках;

показать применение функции в жизни человека.

Методы исследования: наблюдение, беседа, анализ, обобщение, опрос, сравнение.

Глава II. Теоретические сведения.

1.1. Из истории возникновения функции.

Начиная с XVII в. одним из важнейших понятий является понятие функции. Оно сыграло и поныне играет большую роль в познании реального мира.

Идея функциональной зависимости восходит к древности, она содержится уже в первых математически выраженных соотношениями между величинами, в первых правилах действий над числами, в первых формулах для нахождения площади и объёма тех или иных фигур.

Явное и вполне сознательное применение понятия функции и систематическое изучение функциональной зависимости берут своё начало в XVII в. в связи с проникновением в математику идеи переменных. В «Геометрии» Декарта и в работах Ферма, Ньютона и Лейбница понятие функции носило по существу интуитивный характер и было связано либо с геометрическими, либо с механическими представлениями.

Термин «функция» (от латинского function – исполнение , совершение) впервые ввел немецкий математик Готфрид Лейбниц(1646-1716). У него функция связывалась с геометрическим образом (графиком функции). В дальнейшем швейцарский математик Иоганн Бернулли(1667-1748) и член Петербургской Академии наук знаменитый математик XVIII века Леонард Эйлер(1707-1783) рассматривали функцию как аналитическое выражение. У Эйлера имеется и общее понимание функции как зависимости одной переменной величины от другой.

Представление понятия функции на протяжении с XVII в. и до XVIII в. дополнялось и переформулировывалось ведущими учёными И. Бернулли, Л. Эйлером, С. Лакруа, Даламбером, Ж. Фурье, Н.И. Лобачевским. Общее же определение функций сформулировал Дирихле, после длившихся целый век дискуссий в первой половине XIX в.

В общем виде понятие обобщённой функции было введено французом Лораном Шварцем. В 1936 г. 28-летний советский математик и механик Сергей Львович Соболев (ныне академик) первым рассмотрел частный случай обобщённой функции и применил созданную теорию к решению задач математической физики. Важный вклад в развитие теории обобщённых функций внесли ученики и последователи Л. Шварца.

1.2. Виды линейной функции.

Рассмотрим основные существующие виды линейной функции и ее свойства.

1. Постоянная функция.

Постоянной называется функция, заданная формулой у=b, где b – некоторое число.

Графиком постоянной функции у=b является прямая, параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат.

2. Прямая пропорциональность.

Прямой пропорциональностью называется функция, заданная формулой y=kx, где k≠0. Число k называется коэффициентом пропорциональности.

Перечислим свойства функции y=kx:

— область определения функции – множество всех действительных чисел.

— при k0 функция возрастает, а при k убывает на всей числовой прямой.

Графиком прямой пропорциональности y=kx является прямая, проходящая через начало координат.

3. Линейная функция.

Линейной функцией называется функция, которую можно задать формулой y=kx+b , где k и b – действительные числа. Если, в частности, k=0, то получаем постоянную функцию y=b; если b=0, то получаем прямую пропорциональность y=kx.

— область определения функции – множество всех действительных чисел.

— при k0 функция возрастает, а при k убывает на всей числовой оси.

Графиком линейной функции y=kx+b является прямая.

Коэффициенты k и b в уравнении линейной функции y = kx + b, имеют наглядное геометрическое толкование. Значение коэффициента b определяет отрезок, отсекаемый графиком линейной функции на оси ординат, а коэффициент k определяет тангенс угла a, образованного осью абсцисс и прямой; угол отсчитывается от положительного направления оси абсцисс. Если k 0, то образованный угол острый, если k

Взаимное расположение графиков линейных функций.

Если , то графики функций

и пересекаются в одной точке

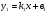
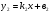
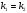
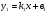
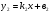
Если , , то графики функций и являются параллельными прямыми

1.1. Линейные зависимости в математике

С применением линейной функциональной зависимости для описания различных реальных процессов я столкнулся уже на уроках математики. Достаточно вспомнить, что расстояние, пройденное пешеходом, поездом, автомашиной при постоянной скорости движения, — линейные функции времени движения. Приведу пример математической задачи.

Задача 1: Автомобиль, выехавший из пункта А в настоящее время находится от него в 10 км. На каком расстоянии S от пункта А будет находиться автомобиль через t часов, если он будет двигаться в том же направлении со скоростью 60 км/ч?

Ответ будет выражаться линейной функцией вида S=60t+10.

Задача 2: Зависимость длины окружности от длины её радиуса.

Опытным путём на уроке математики было установлено, что длина окружности зависит от её радиуса. Эта зависимость выражается формулой C=2πR и является прямой пропорциональной зависимостью с угловым коэффициентом равным 2 π.

Задача 3: Зависимость между градусными мерами смежных углов.

На уроке геометрии мы познакомились со свойством смежных углов. Не трудно заметить, что зависимость их градусных мер является линейной зависимостью k = 180 – b, где k, b – смежные углы.

1.2. Линейные зависимости в физике

Задача1: Скорость распространения звука в воздухе в зависимости от температуры может быть найдена по формуле: v=331+0,6t, v – скорость в м/с, t – температура в градусах Цельсия.

Задача 2: Длина рельсов является линейной функцией температуры: l=l₀(1+at) –линейное расширение твердых тел.

Задача 3: Зависимость давления жидкости на дно сосуда (P) от высоты столба жидкости (h) – линейная зависимость и задаётся формулой: P=gρh, где ρ – плотность жидкости, g≈10

1.3. Линейные зависимости в биологии, экологии и медицине

Задача 1: В биологии тоже встречаются линейные функции. Так, например, из энциклопедии я узнал, что волосы на голове у человека растут примерно со скоростью 0,4 мм в сутки. Таким образом, имеет место формула: l=l₀+0,4t, где l – длина в мм, l₀ – первоначальная длина волос в мм, t – количество дней. Я построил график такой зависимости.

Задача 2: Зависимость численности сине-зелёных водорослей от концентрации общего фосфора в воде выражается следующей формулой: а=0,983р+50,6, где а – численность сине-зелёных водорослей, р – концентрация общего фосфора. Эта зависимость – линейная, и её можно использовать для прогнозирования качества воды. Показателем качества воды служит количество сине-зелёных водорослей. Чем их больше, тем хуже качество воды. На численность сине-зелёных водорослей влияет концентрация фосфорного удобрения, попадающего в водоёмы вместе с талой водой.

1.4. Линейные зависимости в литературе

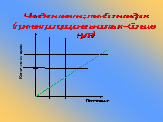
Есть ли линейные функции в устном народном творчестве, например, в поговорках? Вероятно, да! Вот как, на мой взгляд, можно изобразить некоторые из них с помощью графиков линейных функций.

Чем дальше в лес, тем больше дров

(прямая пропорциональность, к – больше нуля)

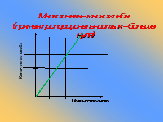
Много снега — много хлеба

(прямая пропорциональность, к – больше нуля)

Дальше в спор — больше слов

(прямая пропорциональность, к – больше нуля)

Больше почёт, больше хлопот.

(прямая пропорциональность, к – больше нуля)

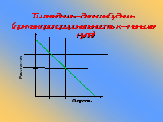
Как аукнется – так и откликнется.

Тише едешь – дальше будешь

(прямая пропорциональность, к – меньше нуля)

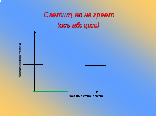
Долго думал, да ничего не выдумал

(линейная функция, к=0)

Светит, но не греет

1.5. Поиск линейных зависимостей в повседневной жизни.

Открытия, сделанные в первой части работы, подтолкнули меня к мысли, что линейные зависимости окружают нас и в повседневной жизни. Я отправился собирать необходимую информацию и проводить новые исследования. Эта работа оказалась не менее увлекательной и интересной. Она побудила меня к творческому процессу: мне захотелось самому найти линейные зависимости в нашей реальной жизни, вывести их задающие формулы, построить графики этих зависимостей.

«Как стоимость телеграммы зависит от количества слов?»

Я посетил отделение связи нашего села с целью увидеть линейную зависимость в профессии почтальон. Выполняя эту работу, я узнал, что эта профессия требует знание линейной функции. Мною были проведены следующие расчеты.

0,95 руб. — стоит одно слово;

12,8 руб. – телеграфный сбор;

Х – количество слов;

У – стоимость телеграммы.

Тогда мы составили формулу стоимости простой телеграммы у = 0,95х + 12,8.

3,25 руб. – стоит одно слово;

12,8 руб. – телеграфный сбор;

Х – количество слов;

У – стоимость телеграммы;

У = 3,25х +12,8. По этой формуле рассчитывают стоимость срочной телеграммы. Данные функции является линейными.

«Расчет стоимости заказного письма».

35 руб. – стоимость 1 г.

21 руб., 33 руб., 18 руб. – стоимость конверта

Х – вес заказного письма

У – стоимость заказного письма У = 35х + 21 , У = 35х + 33, У = 35х + 18,

По данным формулам рассчитывается стоимость заказного письма. Графики данных функций расположены параллельно друг другу.

«Расчет оплаты за коммунальные услуги».

Расчет оплаты по квитанциям за свет и газ так же является линейной зависимостью.

Х – количество потребляемой энергии за месяц

2,04 – стоимость 1кВт

У – стоимость потребляемой энергии за месяц У = 2,04 Х

Х – количество потребляемого газа за месяц

5,086 руб. – цена 1 м 3 газа

У – стоимость потребляемого газа за месяц У = 5,086 Х. Данные функции являются прямой пропорциональностью.

«Расчет полученного урожая фермерским хозяйством»

Мой папа работает фермером. Он выращивает разные культуры: пшеницу, овес, подсолнечник. Я заметил, что количество урожая, полученного моим отцом, имеет линейную зависимость. Я составил следующие формулы.

Х – площадь посаженной культуры

15 ц с 1га — урожайность пшеницы, 25 ц с 1га – урожайность подсолнечника, 10 ц с 1га – урожайность овса.

У – полученный урожай У = 15 Х У = 25 Х У = 10 Х

«Как заработная плата мамы зависит от надоя молока»

Моя мама домохозяйка. Наша семья имеет подсобное хозяйство в котором есть крупный рогатый скот – коровы. Мы реализуем молоко от наших коров в государство. Я заметил, что полученная прибыль от молока имеет линейную зависимость.

15 руб. – стоимость 1л. молока;

Х – количество литров;

У – заработная плата мамы; У = 15 Х

Каждый месяц мама надаивает в среднем 1000 л. молока. Я рассчитал, что ее зарплата в месяц составляет 15000руб.

«Зависимость калорийности молока от его жирности»

Чтобы ответить на вопрос «Как зависит калорийность молока от его жирности?» я отправился в магазин. После сбора информации я увидел, что с увеличением процента жира в молоке калорийность молока увеличивается.