Зачем нужны дифференциальные уравнения в программировании (8 видео)

Что такое дифференциальное уравнение и зачем оно нужно?

На сегодняшний день одним из важнейших навыков для любого специалиста является умение решать дифференциальные уравнения. Решение дифференциальных уравнений – без этого не обходится ни одна прикладная задача, будь это расчет какого-либо физического параметра или моделирование изменений в результате принятой макроэкономической политики. Эти уравнения также важны для ряда других наук, таких как химия, биология, медицина и т.д. Ниже мы приведем пример использования дифференциальных уравнений в экономике, но перед этим кратко расскажем об основных типах уравнений.

Содержание

Дифференциальные уравнения – простейшие виды
Пример применения дифференциального уравнения в экономике
Программирование дифференциальных уравнений в частных производных
Страницы работы
Содержание работы
Зачем нужны дифференциальные уравнения в программировании
🎬 Видео

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Дифференциальные уравнения – простейшие виды

Мудрецы говорили, что законы нашей вселенной написаны на математическом языке. Конечно, в алгебре есть много примеров различных уравнений, но это, большей частью, учебные примеры, неприменимые на практике. По-настоящему интересная математика начинается, когда мы хотим описать процессы, протекающие в реальной жизни. Но как отразить фактор времени, которому подчиняются реальные процессы – инфляция, выработка продукции или демографические показатели?

Вспомним одно важное определение из курса математики, касающееся производной функции. Производная является скоростью изменения функции, следовательно, она может помочь нам отразить фактор времени в уравнении.

То есть, мы составляем уравнение с функцией, которая описывает интересующий нас показатель и добавляем в уравнение производную этой функции. Это и есть дифференциальное уравнение. А теперь перейдем к простейшим типам дифференциальных уравнений для чайников.

Простейшее дифференциальное уравнение имеет вид $y’(x)=f(x)$, где $f(x)$ – некоторая функция, а $y’(x)$ – производная или скорость изменения искомой функции. Оно решается обычным интегрированием: $$y(x)=int f(x)dx.$$

Второй простейший тип называется дифференциальным уравнением с разделяющимися переменными. Такое уравнение выглядит следующим образом $y’(x)=f(x)cdot g(y)$. Видно, что зависимая переменная $y$ также входит в состав конструируемой функции. Уравнение решается очень просто – нужно «разделить переменные», то есть привести его к виду $y’(x)/g(y)=f(x)$ или $dy/g(y)=f(x)dx$. Остается проинтегрировать обе части $$int frac=int f(x)dx$$ – это и есть решение дифференциального уравнения разделяющегося типа.

Последний простой тип – это линейное дифференциальное уравнение первого порядка. Оно имеет вид $y’+p(x)y=q(x)$. Здесь $p(x)$ и $q(x)$ – некоторые функции, а $y=y(x)$ – искомая функция. Для решения такого уравнения применяют уже специальные методы (метод Лагранжа вариации произвольной постоянной, метод подстановки Бернулли).

Есть более сложные виды уравнений – уравнения второго, третьего и вообще произвольного порядка, однородные и неоднородные уравнения, а также системы дифференциальных уравнений. Для их решения нужна предварительная подготовка и опыт решения более простых задач.

Большое значение для физики и, что неожиданно, финансов имеют так называемые дифференциальные уравнения в частных производных. Это значит, что искомая функция зависит от нескольких переменных одновременно. Например, уравнение Блека-Шоулса из области финансового инжиниринга описывает стоимость опциона (вид ценной бумаги) в зависимости от его доходности, размера выплат, а также сроков начала и конца выплат. Решение дифференциального уравнения в частных производных довольно сложное, обычно нужно использовать специальные программы, такие как Matlab или Maple.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Пример применения дифференциального уравнения в экономике

Приведем, как и было обещано, простой пример решения дифференциального уравнения. Вначале поставим задачу.

Для некоторой фирмы функция маржинальной выручки от продажи своей продукции имеет вид $MR=10-0,2q$. Здесь $MR$ – маржинальная выручка фирмы, а $q$ – объем продукции. Нужно найти общую выручку.

Как видно из задачи, это прикладной пример из микроэкономики. Множество фирм и предприятий постоянно сталкивается с подобными расчетами в ходе своей деятельности.

Приступаем к решению. Как известно из микроэкономики, маржинальная выручка представляет собой производную от общей выручки, причем выручка равна нулю при нулевом уровне продаж.

С математической точки задача свелась к решению дифференциального уравнения $R’=10-0,2q$ при условии $R(0)=0$.

Проинтегрируем уравнение, взяв первообразную функцию от обеих частей, получим общее решение: $$R(q) = int (10-0,2q)dq = 10 q-0,1q^2+C. $$

Чтобы найти константу $C$, вспомним условие $R(0)=0$. Подставим: $$R(0) =0-0+C = 0. $$ Значит C=0 и наша функция общей выручки принимает вид $R(q)=10q-0,1q^2$. Задача решена.

Другие примеры по разным типам ДУ собраны на странице: Дифференциальные уравнения с решениями онлайн.

Видео:1. Что такое дифференциальное уравнение?Скачать

Программирование дифференциальных уравнений в частных производных

Страницы работы

Содержание работы

Файл Самостоят_05.doc 4 стр. 146 Кбайт.

1. Программирование дифференциальных уравнений в частных производных.

В данном разделе мы ограничимся рассмотрением методов решений дифференциальных уравнений в частных производных на примере линейных дифференциальных уравнений вида

(01)

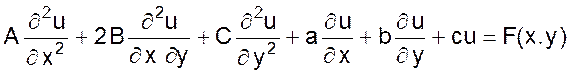
где A, B, C, a, b, c – заданные коэффициенты, которые могут быть постоянными или функциями аргументов x, y;

F(x, y) – заданная функция переменных x и y.

Решение u(x, y) должно удовлетворять уравнению 01 в некоторой области переменных x и y, граница которой задается уравнением Г(x, y) = 0.

В зависимости от знака дискриминанта D = AC – B 2 уравнение 01 можно отнести к одному из типов: эллиптическому (D > 0), параболическому (D = 0), гиперболическому (D 2 ; u(0, t) = u₀(t) = φ₁(t); u_n₊₁(t) = φ₂(t), уравнение 06 для отдельной j-й точки запишем в виде

(08)

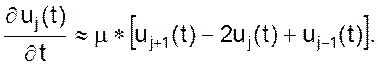
Естественно, для аппроксимации функции 06 в целом нам понадобится система из n обыкновенных дифференциальных уравнений первого порядка.

Представим и решим систему обыкновенных дифференциальных уравнений средствами SIMULINK. Начнем с решения дифференциального уравнения 1 порядка.

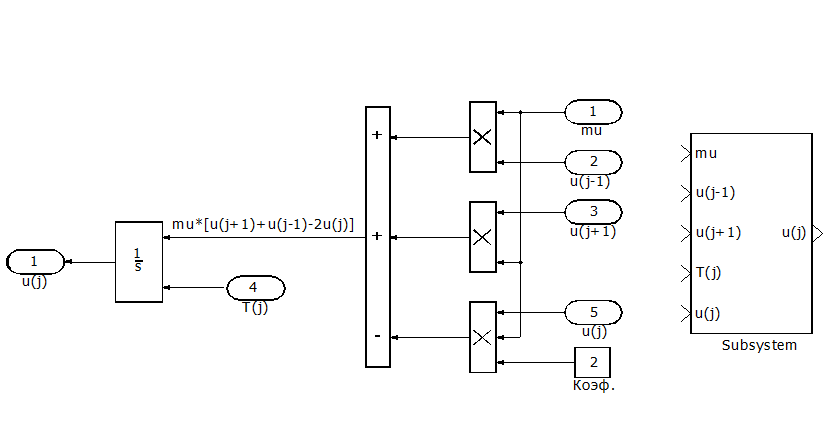
Рис. П6.2. Подсистема «Решение дифференциального уравнения 1 порядка».

Решение левой части уравнения может быть представлено модулем Integrator (с начальным значением) из раздела библиотеки Linear. Правая часть уравнения представляет сумму трех слагаемых. Для ее определения воспользуемся модулями Sum из раздела библиотеки Linear, модулями Product из раздела библиотеки Nonlinear и модулем Constant из раздела библиотеки Sources для задания коэффициента. Объединим блок-схему в подсистему (при этом SIMULINK автоматически подставит в блок-схему модули In и Out) и разметим ее в соответствии с рисунком.

Объединим имеющиеся модули в соответствии с логикой решения системы уравнений и присоединим окно наблюдения за решением.

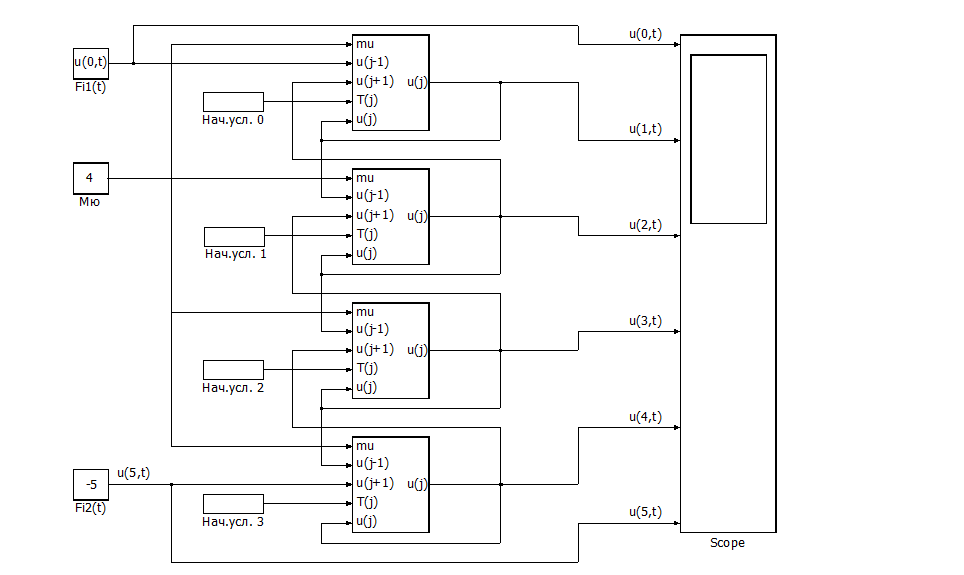
Рис. П6.3. Блок-схема решения задачи[1].

Теперь остается задать начальные условия, значение Мю и функции изменения температуры разделяемых стенкой сред. После чего можно запустить задачу на решение и, получив его, проанализировать.

[1] Программа расположена на файле «Мои документыПрогSIMПосГлава1gla1_05 p6ris3»

Видео:Математика это не ИсламСкачать

Зачем нужны дифференциальные уравнения в программировании

Сразу расшифруем: на студенческом жаргоне дифуры – это дифференциальные уравнения. Часто студентам технических вузов бывает непонятно: зачем им преподают высшую математику? Учитывая тему статьи, ответ будет интересен тем курсантам, которым предстоит служить в войсках и участвовать в боевых действиях.

Понятно, надо знать работу специальных приборов и техники, но зачем высшая математика? Тем более, ни для кого не секрет, что нередко в вузах дают такие знания, которые в жизни никогда не оказываются востребованными.

Чтобы показать полезность знаний, в нашем случае высшей математики, приведём пример построения математической модели боевых действий.

Дополнительным аргументом в пользу нашей точки зрения служит универсальность математики. Имеется в виду то, что одни и те же уравнения часто годятся для описания совершенно разных процессов. Просто, математические символы могут обозначать разные вещи, притом, что решение задачи имеет одно и то же аналитическое выражение.

Модель, которую мы хотим вам предложить, годится как для военных (решение описывает изменение численности подразделения во время боевых действий), так и для описания апериодического процесса колебаний напряжения в электрическом контуре (это важно в задачах из областей связи и телекоммуникаций).

Фредерик Вильям Ланчестер (1868–1946) –
английский эрудит и инженер,
внёс значительный вклад
в автомобилестроение, аэродинамику,
был одним из основателей
теории исследования операций

Итак, ещё в начале прошлого века английский инженер Фредерик Вильям Ланчестер, во время Первой мировой войны, построил ряд математических моделей ведения воздушных сражений. Позже эти модели распространили на случаи боевых действий регулярных войск и партизанских соединений.

Рассмотрим ниже самую простую из таких моделей. Основа нашей модели – дифференциальное уравнение. Из названия уравнения видна необходимость знакомства с понятием производной функции (дифференцирование – это и есть взятие производной). Поэтому скажем об этом несколько слов (точнее, напомним, так как эти понятия входят в школьную программу).

Понятие производной напомним с помощью примера. Если известно, как пройденный телом путь зависит от времени, то мгновенная скорость тела в каждой точке пути как раз и есть производной от пути по времени. Другими словами, мгновенная скорость есть отношение очень малого пути ко времени, за которое тело его проходит (понятно, что и время, соответствующее этому пути, тоже очень мало).

Так, решением алгебраического квадратного уравнения являются два числа (если решение возможно). А вот если уравнение в качестве неизвестной содержит функцию времени и её производные, то такое уравнение называется дифференциальным.

Его решением уже является неограниченно много чисел – целая функция. Тут, правда, надо ещё добавить начальные условия, то есть значения неизвестной функции и её производных меньшего порядка, чем есть в уравнении, в определённый момент времени.

Теперь мы можем рассмотреть нашу модель.

Основная задача нашей модели – выяснить, как меняется численность воюющих сторон со временем при некоторых начальных условиях, о которых скажем ниже. Итак, пусть в боевых действиях участвуют две противоборствующие стороны. Их численный состав обозначим через x(t) и y(t). Начало боевых действий пусть соответствует моменту t = 0 дней.

На деле трудно указать критерии, которые учитывали бы при сравнении противников степень боевой готовности и качество вооружения, способности и опыт командного состава, моральный дух и многие другие факторы. Поэтому сделаем некоторые упрощающие предположения.

Пусть x(t) и y(t) меняются непрерывно и, более того, эти функции имеют производные по времени. Конечно, это упрощение реальной ситуации, поскольку как x(t), так и y(t) – число военных, то есть целое число. Но понятно, что при достаточно больших численных составах каждого из противников увеличение их численности на одного или двух человек даёт на деле очень малую величину по сравнению со всем личным составом.

Поэтому можно считать, что за малые промежутки времени численный состав также изменяется на малые (и даже не целые) количества. Это даст нам возможность искать решение в виде непрерывной функции, что очень упрощает поиск.

Этих соглашений, конечно, недостаточно для того, чтобы выписать конкретные формулы для x(t) и y(t) как функций времени t. Однако, можно указать ряд факторов, которые позволяют описать скорости изменения численности противников.

Обозначим через v_m_х – скорость, с которой сторона х несёт потери от болезней и других факторов, не связанных с боевыми действиями.

Далее, пусть v_w_у – скорость, с которой сторона х несёт потери во время ведения боевых действий со стороной у. Аналогичные обозначения введём для у. Тогда ясно, что скорости изменения x(t) и y(t) можно задать уравнениями

Теперь надо как-то связать эти скорости v_m и v_w с количествами x и y. После чего можно исследовать полученные дифференциальные уравнения, и анализ решения позволит получить сведения о вероятном победителе.

Предположим, что v_m_х = – ax(t) (это значит, что чем большей является численность войск х, тем больше военных могут выйти из строя по болезни, и скорость dx/dt уменьшится). Кроме того, допустим, что v_w_у = – by(t) (то есть, численность х уменьшится под огнём противника пропорционально его численности y). Тогда изменения x(t) можно описать уравнением

Для численности у можно написать аналогичное уравнение.

В уравнениях (1) и (2) а, b, с, d – неотрицательные постоянные, характеризующие степень влияния различных факторов на потери в живой силе обеих сторон х и у. Из них за непосредственные боевые действия отвечают только постоянные b, с. Ещё примем начальные условия: x_о и у_o – численный состав сил х и у в начале боевых действий.

Итак, пусть подразделения противника находятся в зоне действия огневых средств другой стороны, и огонь ведётся только по живой силе, непосредственно участвующей в боевых действиях. Понятно, что совсем непросто вычислить коэффициенты b и с. Один из путей найти их – это представить в виде

где r_у и r_х – удельные коэффициенты огневой мощи сторон у и х (доля огневой мощи, приходящаяся на одного бойца), а р_у и р_х – вероятности того, что каждый из выстрелов со стороны у или х окажется метким.

Отметим далее, что члены, которые соответствуют боевым потерям в уравнениях (1) и (2), являются линейными. Заметим, что Ф. Ланчестер рассматривал и нелинейные модели, которые позволяют описать много интересных особенностей военных действий, но мы для начального знакомства ограничимся линейной моделью.

Предположим, что регулярные войска противников ведут боевые действия в упрощённой ситуации, когда потери, не связанные с боевыми действиями, отсутствуют. Если при этом обе стороны ещё и не получают подкреплений, то математическая модель сводится к системе дифференциальных уравнений

Разделив второе уравнение на первое, получим

Интегрируя последнее уравнение (4) с учетом начальных условий, приходим к равенству

Соотношение (5) объясняет, почему систему (3) называют моделью с квадратичным законом. Если обозначить через К постоянную by_о 2 – cx_о 2 , то уравнение

Рис. 1

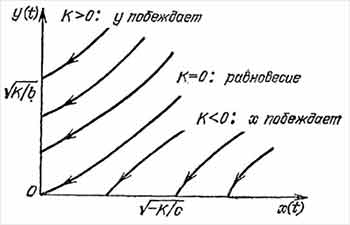
описывает гиперболу (или пару прямых при К = 0). Такую систему можно назвать дифференциальной системой с гиперболическим законом.

На рис. 1 изображены гиперболы для различных значений К, при этом ясно, что следует рассматривать лишь первый квадрант (так как х ≥ 0 и у ≥ 0). Стрелки на кривых указывают направление изменения численности сил с течением времени.

Чтобы ответить на вопрос, кто побеждает в построенной модели (3), условимся, прежде всего, говорить, что побеждает сторона у (или х), если она первой уничтожает боевые силы стороны х (или у). Так, в случае, если К > 0, побеждает сторона у, ибо в соответствии с уравнением (5) переменная у никогда не обращается в нуль, в то время как при значении y = (K/b) 1/2 переменная х обращается в нуль. Таким образом, чтобы победили силы у, им нужно стремиться достичь такой ситуации, при которой К > 0, то есть, когда

Из равенств (2) следует, что неравенство (7) можно переписать в виде

Левая часть этого неравенства показывает, что изменения в отношении сил y_о/x_о дают преимущество одной из сторон в соответствии с квадратичным законом! Так, например, изменение в отношении сил от y_о/x_о = 1 до y_о/x_о = 2 даёт четырехкратное преимущество силам у. Отметим правда, что уравнение (5) определяет соотношение между силами противников, не учитывая их зависимости от времени.

На всё, о чем выше было написано, автора вдохновила замечательная популярная книжка В.В. Амелькина «Дифференциальные уравнения в приложениях». Но в рамках нашей темы, как раз при построении временной зависимости для численности войск в рассмотренном в книге примере была допущена досадная, но существенная ошибка.

Перед тем, как продолжить чтение, попробуйте самостоятельно обнаружить эту ошибку. Хочу подчеркнуть, что эта ошибка нисколько не снижает ценности книги, к тому же написанной понятным языком, доступно для школьника, интересующегося математикой. Ниже приводится правильное решение.

Чтобы вывести формулы для временной зависимости численных составов, поступим следующим образом. Продифференцируем по t первое из уравнений системы (3) и подставим в него второе уравнение этой же системы. В результате придём к дифференциальному уравнению второго порядка, так называют уравнения, которые содержат вторую производную от неизвестной функции

Используя тогда в качестве начальных условий соотношения

получим решение уравнения (9) в виде

где chх = (е х +е –х )/2 и shх = (е х – е –х )/2 – гиперболические функции, b = (bc) 1/2 , g = (b/c) 1/2 . Эти функции напоминают тригонометрические (например, ch 2 х – sh 2 х = 1). Но cosx и sinx имеют колебательный характер, а chх и shх экспоненциально растут или падают, как это видно из их графиков на рис. 2 (график функции у = sh х) и 3 (график функции у = ch х). В вышеназванной книге выписаны решения другого уравнения – d 2 x/dt 2 + bсx = 0, а это – cosx и sinx.

Подобно формуле (10), можно получить решение для y(t) (сделайте это самостоятельно) в виде

На рис. 4 показаны графики функций, заданных уравнениями (10) и (11), в случае, когда К > 0 (т. е. когда by_о 2 > cx_о 2 или когда γy_о > x_о).

В заключение отметим, что для победы сил стороны у не обязательно, чтобы число y_о было больше числа x_о. Требуется лишь выполнение неравенства γy_о > x_о.

Если теперь под х(t) и у(t) понимать заряд q и электрический ток I = dq/dt, то мы придём к описанию апериодического процесса в электрической цепи. Более сложными и более соответствующими описываемому событию являются нелинейные модели.

Например, уравнение dN/dt = aN – bN 2 – основа дифференциальной модели популяций, которая связана с размножением или вымиранием животных, а также с сосуществованием различных их видов в ситуации «хищник – жертва».

Мы коснулись надводной части айсберга с именем «теория дифференциальных уравнений», которая на рубеже тысячелетий претерпела основательные изменения. Ничего не было сказано о нелинейной динамике, детерминированном хаосе и многом другом, что привело к новому пониманию необычных природных явлений.

Одним из таких явлений природы стала турбулентность, отражающая качественный переход к другой форме движения. В этом явлении и сегодня остаётся много загадок. Видимо, ещё не всё открыто, и молодому поколению есть, где приложить силы в познании окружающего мира.

А.М. Пальти , преподаватель физики