За что отвечает с в графике функции квадратного уравнения

В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.

Функция вида , где 0″ title=»a0″/> называется квадратичной функцией.

В уравнении квадратичной функции:

a — старший коэффициент

b — второй коэффициент

с — свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид:

Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов.

График функции имеет вид:

Для нахождения координат базовых точек составим таблицу:

Обратите внимание, что график функции симметричен графику функции относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0 , то ветви параболы напрaвлены вверх .

Если старший коэффициент a , то ветви параболы напрaвлены вниз .

Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции — это точки пересечения графика функции с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .

В случае квадратичной функции нужно решить квадратное уравнение .

В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:

1. Если ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если 0″ title=»a>0″/>,то график функции выглядит как-то так:

2. Если ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если 0″ title=»a>0″/>,то график функции выглядит примерно так:

3 . Если 0″ title=»D>0″/>,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:

,

Если 0″ title=»a>0″/>,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции — координаты вершины параболы:

Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.

И еще один параметр, полезный при построении графика функции — точка пересечения параболы с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: .

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

Итак, основные параметры графика квадратичной функции показаны на рисунке:

Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.

1. Функция задана формулой .

Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции

1. Направление ветвей параболы.

Так как 0″ title=»a=2>0″/>,ветви параболы направлены вверх.

2. Найдем дискриминант квадратного трехчлена

0″ title=»D=b^2-4ac=9-4*2*(-5)=49>0″/>

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.

Для того, чтобы найти их координаты, решим уравнение:

,

3. Координаты вершины параболы:

4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.

Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.

1. Найдем координаты вершины параболы.

2. Найдем координаты точек, стоящих справа и слева от вершины.

Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы

Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3

Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2

Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией:

2 . Уравнение квадратичной функции имеет вид — в этом уравнении — координаты вершины параболы

или в уравнении квадратичной функции , и второй коэффициент — четное число.

Построим для примера график функции .

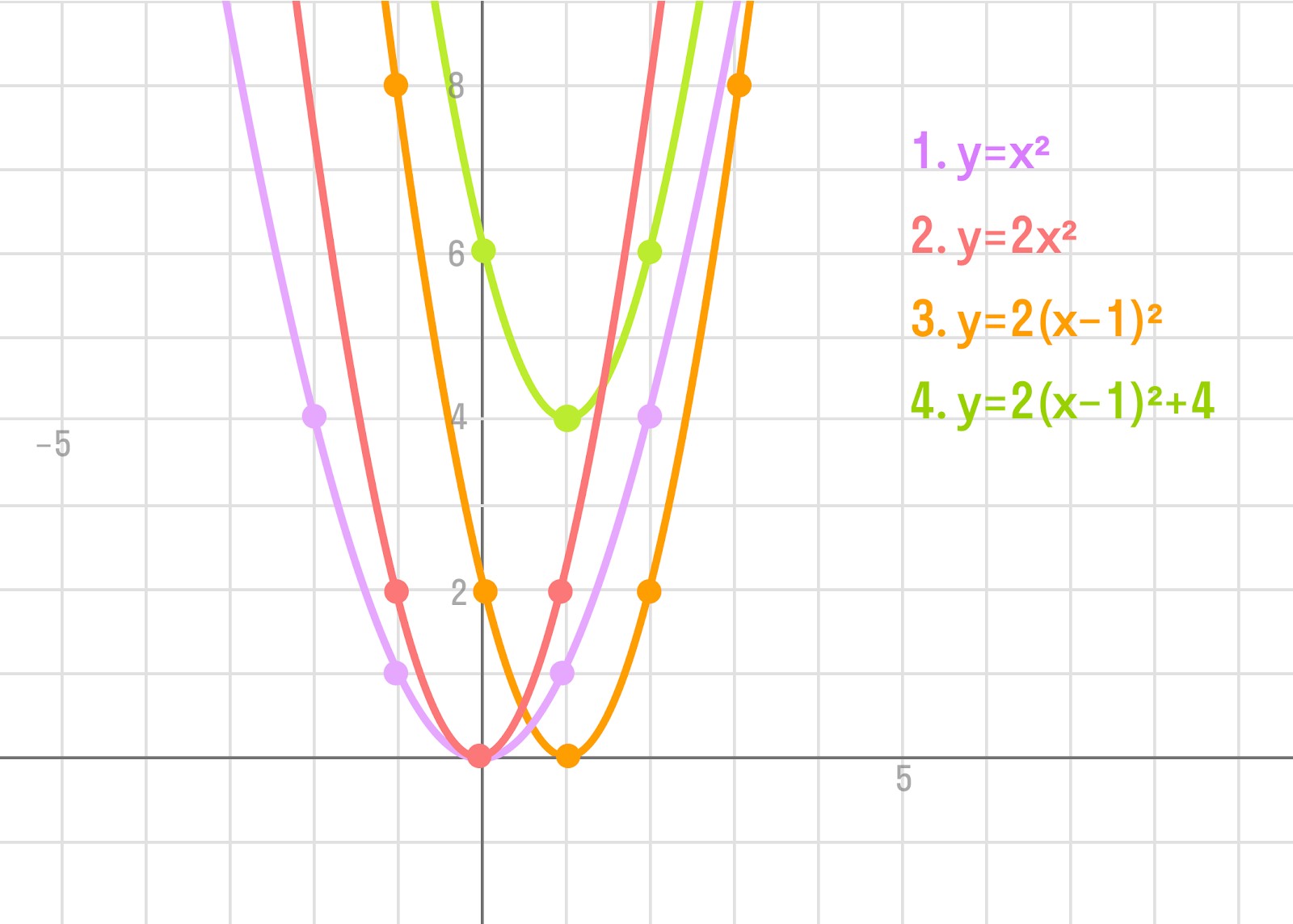
Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно

• сначала построить график функции ,
• затем одинаты всех точек графика умножить на 2,
• затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• а затем вдоль оси OY на 4 единицы вверх:

Теперь рассмотрим построение графика функции . В уравнении этой функции , и второй коэффициент — четное число.

Выделим в уравнении функции полный квадрат:

Следовательно, координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3 . Уравнение квадратичной функции имеет вид y=(x+a)(x+b)

Построим для примера график функции y=(x-2)(x+1)

1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:

(х-2)(х+1)=0, отсюда

2. Координаты вершины параболы:

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.

Нанесем эти точки на координатную плоскость и построим график:

График квадратичной функции.

Перед вами график квадратичной функции вида .

Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции от значения коэффициента ,
— сдвига графика функции вдоль оси от значения ,

— сдвига графика функции вдоль оси от значения
— направления ветвей параболы от знака коэффициента
— координат вершины параболы от значений и :

И.В. Фельдман, репетитор по математике.

Видео:Определение знаков коэффициентов квадратного уравнения (параболы) по рисунку/ЗНО 2010 #25Скачать

Как определить a, b и c по графику параболы

Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.

Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

1 способ – ищем коэффициенты на графике

Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.

Коэффициент (a) можно найти с помощью следующих фактов:

— Если (a>0), то ветви параболы направленных вверх, если (a 1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:

Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.

Решаем систему.
Пример:

Вычтем из второго уравнения первое:

Подставим (9a) вместо (b):

Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:

Подставим в первое уравнение (a):

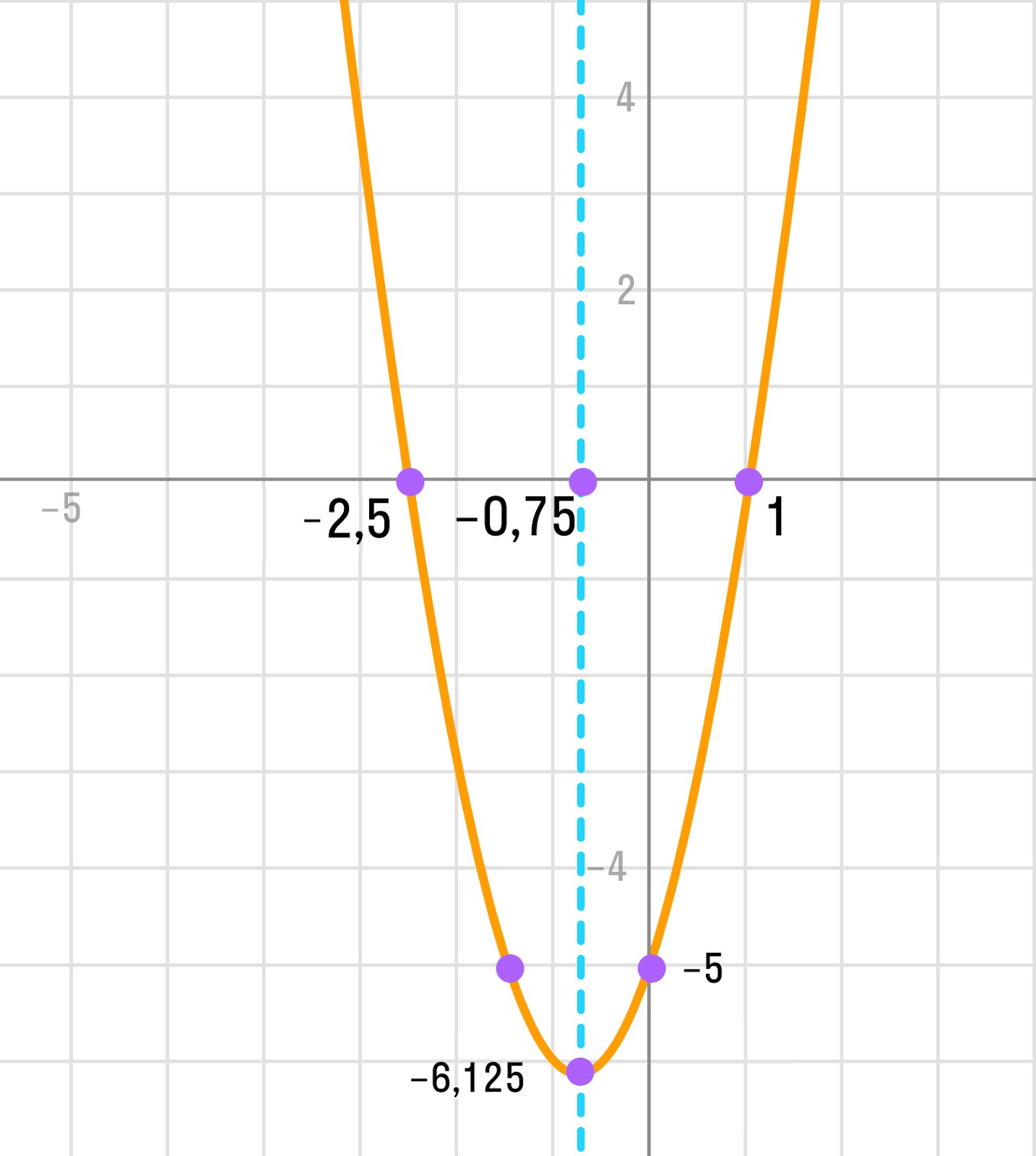
Получается квадратичная функция: (y=-x^2-9x-15).

Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:

Сложим 2 уравнения:

Подставим во второе уравнение:

Теперь найдем точки пересечения двух функций:

Теперь можно найти ординату второй точки пересечения:

Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

3 способ – используем преобразование графиков функций

Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.

Главный недостаток этого способа — вершина должна иметь целые координаты.

Сам способ базируется на следующих идеях:

График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).

– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.

– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
— График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.

График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.

У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:

Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).

Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).

Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).

Видео:Квадратичная функция и ее график. 8 класс.Скачать

Квадратичная функция. Построение параболы

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Видео:Квадратичная функция за 5 минутСкачать

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило, в соответствии с которым каждому значению аргумента соответствует единственное значение функции. Вот какими способами ее можно задать:

• Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ: наглядно.

• Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

График функции — это объединение всех точек координатной плоскости, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.

Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.

Видео:Построение графика квадратичной функцииСкачать

Построение квадратичной функции

Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0.

График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 в частном случае при b = 0, c = 0:

Точки, обозначенные фиолетовыми кружками, называют базовыми точками. Чтобы найти их координаты для функции y = x 2 , нужно составить таблицу:

x

y

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов. При увеличении старшего коэффициента график сужается, при уменьшении — расширяется.

График функции y = –x 2 выглядит, как перевернутая парабола:

Зафиксируем координаты базовых точек в таблице:

x

y

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

• Если старший коэффициент больше нуля (a > 0), то ветви параболы напрaвлены вверх.
• Если старший коэффициент меньше нуля (a 2 + bx + c. Чтобы найти точки пересечения с осью Ox, нужно решить квадратное уравнение ax 2 + bx + c = 0. В процессе найдем дискриминант D = b 2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.

Рассмотрим три случая:

1. Если D 0,то график выглядит так:

1. Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
2. Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:

Если a > 0, то график выглядит как-то так:

0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>

Теперь понятно, что, зная направление ветвей параболы и знак дискриминанта, мы можем схематично представить график конкретной функции.

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

Видео:Парабола / квадратичная функция / влияние коэффициентовСкачать

Алгоритм построения параболы

Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.

Видео:Задание 10 Квадратичная функция Знаки коэффициентов а и сСкачать

Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.

Разберем общий алгоритм на примере y = 2x 2 + 3x — 5.

Как строим:

1. Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена 2x 2 + 3x — 5.

D = b 2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0

В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:

Точка пересечения с осью OY находится: (0; -5) относительно оси симметрии.

Нанесем эти точки на координатную плоскость и построим график параболы:

Видео:ТЕПЕРЬ ТЫ ЛЕГКО ПОЙМЕШЬ свойства квадратичной функции — ПараболаСкачать

Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀

Зная координаты вершины параболы и старший коэффициент, можно записать уравнение квадратичной функции в виде у = a(x − x₀) + y₀, где x₀, y₀ — координаты вершины параболы.

Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x 2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.

Рассмотрим пример: y = 2 * (x — 1) 2 + 4.

Как строим:

1. Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:

• построить график функции y = x 2 ,
• умножить ординаты всех точек графика на 2,
• сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• сдвинуть его вдоль оси OY на 4 единицы вверх.

Построить график параболы для каждого случая.



Видео:Как легко составить уравнение параболы из графикаСкачать



Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)

Рассмотрим следующий пример: y = (x − 2) × (x + 1).

Как строим:

Данный вид функции позволяет быстро найти нули функции:

(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.

Определим координаты вершины параболы:



Найти точку пересечения с осью OY:

с = ab = (−2) × (1) = −2 и ей симметричная относительно оси симметрии параболы.

Отметим эти точки на координатной плоскости и соединим плавной прямой линией.

🎦 Видео

Как построить график функции без таблицыСкачать



Как найти все коэффициенты параболы по графику? Большой ответ на этот вопрос.Скачать



Как определить уравнение параболы по графику?Скачать



Алгебра 9 класс (Урок№10 - Построение графика квадратичной функции.)Скачать



Построение графика квадратичной функции. Алгебра, 9 классСкачать



Парабола. Квадратичная функцияСкачать



График квадратичной функции с модулемСкачать



Функция у=х² и у=х³ и их графики. Алгебра, 7 классСкачать



Парабола | Квадратный трёхчлен #2 | Ботай со мной #021 | Борис ТрушинСкачать



Уравнение параболы #алгебра #графики #парабола #репетиторСкачать