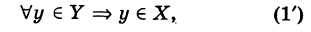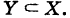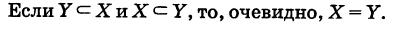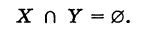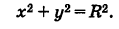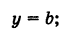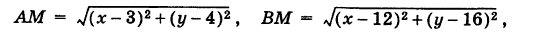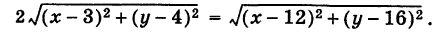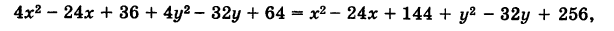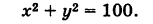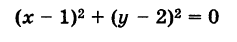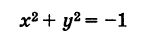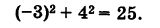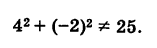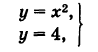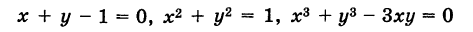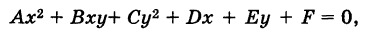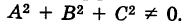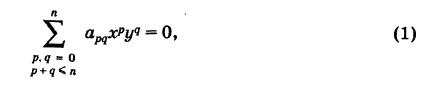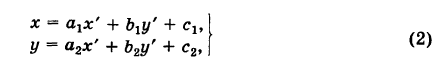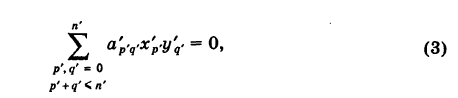Явное и неявное уравнение линии

В прошлом материале мы рассмотрели основные моменты, касающиеся темы прямой на плоскости. Теперь же перейдем к изучению уравнения прямой: рассмотрим, какое уравнение может называться уравнением прямой, а также то, какой вид имеет уравнение прямой на плоскости.

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Определение уравнения прямой на плоскости

Допустим, что есть прямая линия, которая задана в прямоугольной декартовой системе координат O х у .

Прямая линия – это геометрическая фигура, которая состоит из точек. Каждая точка имеет свои координаты по осям абсцисс и ординат. Уравнение, которое описывает зависимость координат каждой точки прямой в декартовой системе O x y , называется уравнением прямой на плоскости.

Фактически, уравнение прямой на плоскости – это уравнение с двумя переменными, которые обозначаются как x и y . Уравнение обращается в тождество при подстановке в него значений любой из точек прямой линии.

Давайте посмотрим, какой вид будет иметь уравнение прямой на плоскости. Этому будет посвящен весь следующий раздел нашей статьи. Отметим, что существует несколько вариантов записи уравнения прямой. Объясняется это наличием нескольких способов задания прямой линии на плоскости, и также различной спецификой задач.

Видео:Видеоурок "Параметрические уравнения прямой"Скачать

Общее уравнение прямой линии

Познакомимся с теоремой, которая задает вид уравнения прямой линии на плоскости в декартовой системе координат O x y .

Уравнение вида A x + B y + C = 0 , где x и y – переменные, а А , В и C – это некоторые действительные числа, из которых A и B не равны нулю, задает прямую линию в декартовой системе координат O x y . В свою очередь, любая прямая линия на плоскости может быть задана уравнением вида A x + B y + C = 0 .

Таким образом, общее уравнение прямой на плоскости имеет вид A x + B y + C = 0 .

Поясним некоторые важные аспекты темы.

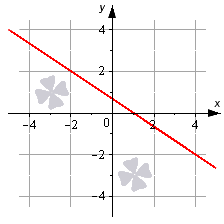
Посмотрите на рисунок.

Линия на чертеже определяется уравнением вида 2 x + 3 y — 2 = 0 , так как координаты любой точки, составляющей эту прямую, удовлетворяют приведенному уравнению. В то же время, определенное количество точек плоскости, определяемых уравнением 2 x + 3 y — 2 = 0 , дают нам прямую линию, которую мы видим на рисунке.

Общее уравнение прямой может быть полным и неполным. В полном уравнении все числа А , В и C отличны от нуля. Во всех остальных случаях уравнение считается неполным. Уравнение вида A x + B y = 0 определяет прямую линию, которая проходит через начало координат. Если A равно нулю, то уравнение A x + B y + C = 0 задает прямую, расположенную параллельно оси абсцисс O x . Если B равно нулю, то линия параллельна оси ординат O y .

Вывод: при некотором наборе значений чисел А , В и C с помощью общего уравнения прямой можно записать любую прямую линию на плоскости в прямоугольной системе координат O х у .

Прямая, заданная уравнением вида A x + B y + C = 0 , имеет нормальный вектор прямой с координатами A , B .

Все приведенные уравнения прямых, которые мы рассмотрим ниже, могут быть получены из общего уравнения прямой. Также возможен и обратный процесс, когда любое из рассматриваемых уравнений может быть приведено к общему уравнению прямой.

Разобраться во всех нюансах темы можно в статье «Общее уравнение прямой». В материале мы приводим доказательство теоремы с графическими иллюстрациями и подробным разбором примеров. Особое внимание в статье уделяется переходам от общего уравнения прямой к уравнениям других видов и обратно.

Видео:Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Уравнение прямой в отрезках

Уравнение прямой в отрезках имеет вид x a + y b = 1 , где a и b – это некоторые действительные числа, которые не равны нулю. Абсолютные величины чисел a и b равны длине отрезков, которые отсекаются прямой линией на осях координат. Длина отрезков отсчитывается от начала координат.

Благодаря уравнению можно легко построить прямую линию на чертеже. Для этого необходимо отметить в прямоугольной системе координат точки a , 0 и 0 , b , а затем соединить их прямой линией.

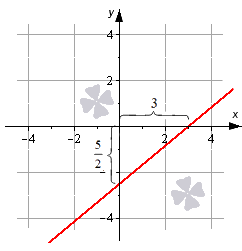
Построим прямую, которая задана формулой x 3 + y — 5 2 = 1 . Отмечаем на графике две точки 3 , 0 , 0 , — 5 2 , соединяем их между собой.

Дополнительно рекомендуем ознакомиться с материалом, изложенным в статье «Уравнение прямой в отрезках».

Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать

Уравнение прямой с угловым коэффициентом

Эти уравнения, имеющие вид y = k · x + b должны быть нам хорошо известны из курса алгебры. Здесь x и y – это переменные, k и b – это некоторые действительные числа, из которых k представляет собой угловой коэффициент. В этих уравнениях переменная у является функцией аргумента x .

Дадим определение углового коэффициента через определение угла наклона прямой к положительному направлению оси O x .

Для обозначения угла наклона прямой к положительному направлению оси O x в декартовой системе координат введем величину угла α . Угол отсчитывается от положительного направления оси абсцисс до прямой линии против хода часовой стрелки. Угол α считается равным нулю в том случае, если линия параллельна оси O x или совпадает с ней.

Угловой коэффициент прямой – это тангенс угла наклона этой прямой. Записывается это следующим образом k = t g α . Для прямой, которая располагается параллельно оси O y или совпадает с ней, записать уравнение прямой с угловым коэффициентом не представляется возможным, так как угловой коэффициент в этом случае превращается в бесконечность (не существует).

Прямая, которая задана уравнением y = k · x + b , проходит через точку 0 , b на оси ординат. Это значит, что уравнение прямой с угловым коэффициентом y = k · x + b , задает на плоскости прямую линию, которая проходит через точку 0 , b и образует угол α с положительным направлением оси O x , причем k = t g α .

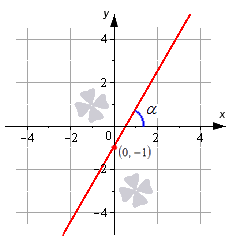
Изобразим прямую линию, которая определяется уравнением вида y = 3 · x — 1 .

Эта линия должна пройти через точку ( 0 , — 1 ) . Угол наклона α = a r c t g 3 = π 3 равен 60 градусов к положительному направлению оси O x . Угловой коэффициент равен 3

Обращаем ваше внимание, что с помощью уравнения прямой с угловым коэффициентом очень удобно искать уравнение касательной к графику функции в точке.

Больше материала по теме можно найти в статье «Уравнение прямой с угловым коэффициентом». Помимо теории там размещено большое количество графических примеров и подробный разбор задач.

Видео:Уравнение прямой в пространстве. 11 класс.Скачать

Каноническое уравнение прямой на плоскости

Данный вид уравнения имеет вид x — x 1 a x = y — y 1 a y , где x 1 , y 1 , a x , a y — это некоторые действительные числа, из которых a x и a y не равны нулю.

Прямая линия, заданная каноническим уравнением прямой, проходит через точку M 1 ( x 1 , y 1 ) . Числа a x и a y в знаменателях дробей представляют собой координаты направляющего вектора прямой линии. Это значит, что каноническое уравнение прямой линии x — x 1 a x = y — y 1 a y в декартовой системе координат O x y соответствует линии, проходящей через точку M 1 ( x 1 , y 1 ) и имеющей направляющий вектор a → = ( a x , a y ) .

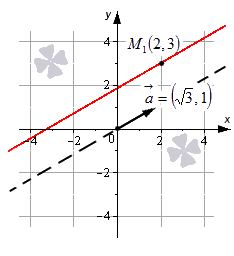
Изобразим в системе координат O x y прямую линию, которая задается уравнением x — 2 3 = y — 3 1 . Точка M 1 ( 2 , 3 ) принадлежит прямой, вектор a → ( 3 , 1 ) является направляющим вектором этой прямой линии.

Каноническое уравнение прямой линии вида x — x 1 a x = y — y 1 a y может быть использовано в случаях, когда a x или a y равно нулю. Наличие ноля в знаменателе делает запись x — x 1 a x = y — y 1 a y условной. Уравнение можно записать следующим образом a y ( x — x 1 ) = a x ( y — y 1 ) .

В том случае, когда a x = 0 , каноническое уравнение прямой принимает вид x — x 1 0 = y — y 1 a y и задает прямую линию, которая расположена параллельно оси ординат или совпадает с этой осью.

Каноническое уравнение прямой при условии, что a y = 0 , принимает вид x — x 1 a x = y — y 1 0 . Такое уравнение задает прямую линию, расположенную параллельно оси абсцисс или совпадающую с ней.

Больше материала на тему канонического уравнения прямой смотрите здесь. В статье мы приводим целый ряд решений задач, а также многочисленные примеры, которые позволяют лучше овладеть темой.

Видео:9 класс, 5 урок, Уравнение линии на плоскостиСкачать

Параметрические уравнения прямой на плоскости

Данные уравнения имеют вид x = x 1 + a x · λ y = y 1 + a y · λ , где x 1 , y 1 , a x , a y — это некоторые действительные числа, из которых a x и a y не могут быть одновременно равны нулю. В формулу вводится дополнительный параметр λ , который может принимать любые действительные значения.

Назначение параметрического уравнения в том, чтобы установить неявную зависимости между координатами точек прямой линии. Для этого и вводится параметр λ .

Числа x , y представляют собой координаты некоторой точки прямой. Они вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра λ .

Предположим, что λ = 0 .

Тогда x = x 1 + a x · 0 y = y 1 + a y · 0 ⇔ x = x 1 y = y 1 , т. е. точка с координатами ( x 1 , y 1 ) принадлежит прямой.

Обращаем ваше внимание на то, что коэффициенты a x и a y при параметре λ в данном виде уравнений представляют собой координаты направляющего вектора прямой линии.

Рассмотрим параметрические уравнения прямой линии вида x = 2 + 3 · λ y = 3 + λ . Прямая, заданная уравнениями, в декартовой системе координат проходит через точку ( x 1 , y 1 ) и имеет направляющий вектор a → = ( 3 , 1 ) .

Больше информации ищите в статье «Параметрические уравнения прямой на плоскости».

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Нормальное уравнение прямой

Нормальное уравнение прямой имеет вид , A x + B y + C = 0 , где числа А , В , и C таковы, что длина вектора n → = ( A , B ) равна единице, а C ≤ 0 .

Нормальным вектором линии, заданной нормальным уравнением прямой в прямоугольной системе координат O х у , является вектор n → = ( A , B ) . Эта прямая проходит на расстоянии C от начала координат в направлении вектора n → = ( A , B ) .

Еще одним вариантом записи нормального уравнения прямой линии является cos α · x + cos β · y — p = 0 , где cos α и cos β — это два действительных числа, которые представляют собой направляющие косинусы нормального вектора прямой единичной длины. Это значит, что n → = ( cos α , cos β ) , справедливо равенство n → = cos 2 α + cos 2 β = 1 , величина p ≥ 0 и равна расстоянию от начала координат до прямой.

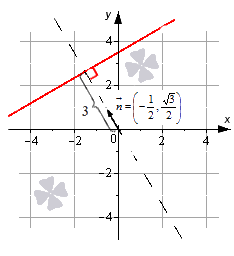
Рассмотрим общее уравнение прямой — 1 2 · x + 3 2 · y — 3 = 0 . Это общее уравнение прямой является нормальным уравнением прямой, так как n → = A 2 + B 2 = — 1 2 2 + 3 2 = 1 и C = — 3 ≤ 0 .

Уравнение задает в декартовой системе координат 0ху прямую линию, нормальный вектор которой имеет координаты — 1 2 , 3 2 . Линия удалена от начала координат на 3 единицы в направлении нормального вектора n → = — 1 2 , 3 2 .

Обращаем ваше внимание на то, что нормальное уравнение прямой на плоскости позволяет находить расстояние от точки до прямой на плоскости.

Если в общем уравнении прямой A x + B y + C = 0 числа А , В и С таковы, что уравнение A x + B y + C = 0 не является нормальным уравнением прямой, то его можно привести к нормальному виду. Подробнее об этом читайте в статье «Нормальное уравнение прямой».

Видео:Видеоурок "Общие уравнения прямой"Скачать

Уравнение линии — определение с примерами решения

Содержание:

Множества:

Под множеством X = понимается собрание (совокупность) некоторых элементов х, х х’ . . Если х есть элемент множества X, то пишут х € X (читается: х принадлежит X); если у не является элементом множества X, то пишут у t X (читается: у не принадлежит множеству X).

Пример:

X — множество всех студентов в данной аудитории.

Пример:

Х = — множество натуральных чисел.

Удобно ввести понятие пустого множества

Пример:

Множество трехголовых людей пусто.

Множества X и X’ считаются равными, т. е. X = X’, если они состоят из одних и тех же элементов.

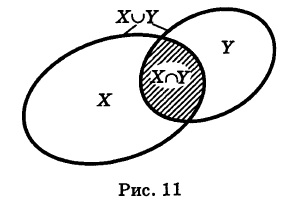
Определение: Множество У, состоящее из части элементов множества X или совпадающее с ним, называется подмножеством множества X; в этом случае пишут

Условились считать, что пустое множество есть подмножество любого множества.

Если множества изображать «логическими фигурами», то соотношению (1) соответствует рис. 10.

Если под символом V понимать «для любого», то соотношение (1) эквивалентно следующему:

где стрелка 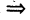заменяет слово «следует».

Пример:

Пусть X — множество всех студентов первого курса, У — множество студенток первого курса. Очевидно,

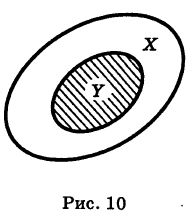
Определение: Под объединением (суммой) двух множеств X и Y понимается множество X U У (U — знак объединения), состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств, т. е. входящих или в X, или в У, или в X и в У одновременно (рис. 11).

Аналогично определяется объединение большего числа множеств. Так, под объединением X U У U Z трех множеств понимается множество всех элементов, принадлежащих хотя бы одному из множеств X, У, Z. Логически знак объединения множеств соответствует союзу «или» (соединительному).

Определение: Под пересечением (произведением) двух множеств X и У понимается множество 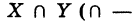знак пересечения), состоящее из всех элементов, принадлежащих как одному у так и другому множествам, т. е. входящих ив множество X, и в множество У (общая часть множеств) (рис. 11).

Таким образом, знак пересечения множеств логически соответствует союзу «и». Если множества X и У не имеют общих элементов, то их пересечение пусто:

Аналогично определяется пересечение большего числа множеств. Так, под пересечением 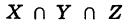трех множеств понимается множество всех элементов, принадлежащих одновременно множествам X, Y и Z.

Например: = = .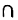

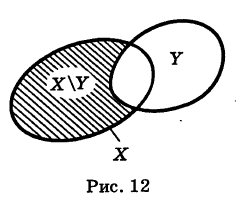
Определение: Для множеств X и У под их разностью ХУ понимается множество, содержащее все элементы множества X, не входящие в множество У (рис. 12).

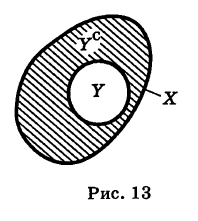
Если У X, то множество Ус = ХУ называется дополнением множества У до множества X (рис. 13).

Очевидно, .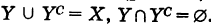

Например: = .

Видео:Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

Метод координат на плоскости

Раздел математики, занимающийся изучением свойств геометрических фигур с помощью алгебры, носит название аналитической геометрии, а использование для этой цели координат называется методом координат.

Выше мы применили метод координат для решения ряда важных, но частных задач. Теперь мы приступим к систематическому изложению того, как в аналитической геометрии решается общая задача, состоящая в исследовании методами математического анализа формы, расположения и свойств данной линии.

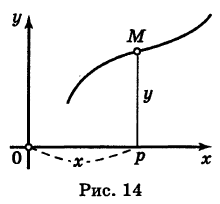
Пусть мы имеем некоторую линию на плоскости (рис. 14). Координаты х и у точки М, лежащей на этой линии, не могут быть вполне произвольными; они должны быть подчинены известным ограничениям, обусловленным геометрическими свойствами данной линии. Тот факт, что числа х и у являются координатами точки, лежащей на данной линии, аналитически записывается в виде некоторого уравнения. Это уравнение называется уравнением линии на плоскости.

Сущность метода координат на плоскости заключается в том, что всякой плоской линии сопоставляется ее уравнение1*, а затем свойства этой линии изучаются путем аналитического исследования соответствующего уравнения.

Линия как множество точек

Линия на плоскости обычно задается как множество точек, обладающих некоторыми геометрическими свойствами, исключительно им присущими.

Пример:

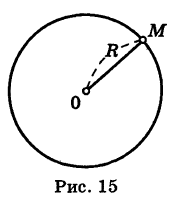
Окружность радиуса R (рис. 15) есть множество всех точек плоскости, удаленных на расстояние R от некоторой ее точки О (центр окружности).

Иными словами, на окружности расположены те и только те точки, расстояние которых от центра окружности равно ее радиусу.

Пример:

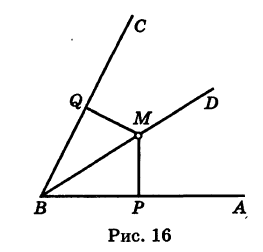
Биссектриса угла ABC (рис. 16) есть множество всех точек, лежащих внутри угла и равноудаленных от его сторон. Этим утверждается, что: 1) для каждой точки М, лежащей на биссектрисе BZ), длины перпендикуляров MP и MQ, опущенных соответственно на стороны ВА и ВС угла, равны между собой: MP = MQ, и 2) всякая точка, находящаяся внутри угла ABC и не лежащая на его биссектрисе, будет ближе к одной стороне угла, чем к другой.

Видео:14. Что такое параметрически заданная функция, производная параметрически заданной функции.Скачать

Уравнение линии на плоскости

Сформулируем теперь точнее определение уравнения линии1* на плоскости.

Определение: Уравнением линии (уравнением кривой) на плоскости Оху называется уравнение, которому удовлетворяют координаты х и у каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Таким образом, для того чтобы установить, что данное уравнение является уравнением некоторой линии К, необходимо и достаточно: 1) доказать, что координаты .любой точки, лежащей на линии К у удовлетворяют этому уравнению, и 2) доказать, обратно, что если координаты некоторой точки удовлетворяют этому уравнению, то точка обязательно лежит на линии К.

Отсюда уже автоматически будет следовать, что: 1′) если координаты какой-нибудь точки не удовлетворяют данному уравнению, то точка эта не лежит на линии К, и 2′) если точка не лежит на линии К, то ее координаты не удовлетворяют данному уравнению.

Если точка М (*, у) передвигается по линии К, то ее координаты х и у, изменяясь, все время удовлетворяют уравнению этой кривой. Поэтому координаты точки М (х, у) называются текущими координатами точки линии К.

На плоскости Оху текущие координаты точки М данной кривой К обычно обозначаются через х и у, причем первая из них есть абсцисса точки М, а вторая — ее ордината. Однако, если это целесообразно, текущие координаты точки М можно обозначать.

Линию мы часто будем называть кривой независимо от того, прямолинейна она или не прямолинейна любыми буквами, например М (X, У) или М 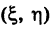и т. п. Так, например, уравнения

где точки N (х, у) и N (X, У) расположены на плоскости Оху, представляют собой уравнение одной и той же прямой на этой плоскости.

Основное понятие аналитической геометрии — уравнение линии — поясним на ряде примеров.

Пример:

Составить уравнение окружности данного радиуса R с центром в начале координат.

Решение:

Возьмем на окружности (рис. 17) произвольную точку М (х, у) и соединим ее с центром О. По определению окружности имеем ОМ = R,

т. е. 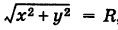, откуда

Уравнение (1) связывает между собой координаты х и у каждой точки данной окружности. Обратно, если координаты точки М (х, у) удовлетворяют уравнению (1), то, очевидно, ОМ = R и, следовательно, эта точка лежит на нашей окружности. Таким образом, уравнение (1) представляет собой уравнение окружности радиуса R с центром в начале координат.

Пример:

Составить уравнения биссектрис координатных углов.

Решение:

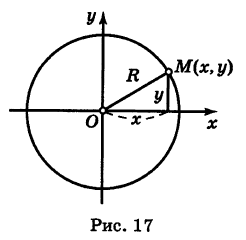
Рассмотрим сначала биссектрису I и III координатных углов (рис. 18, а). Возьмем на ней произвольную точку М (х, у). Если точка М лежит в I квадранте, то абсцисса и ордината ее обе положительны и равны между собой (по свойству биссектрисы). Если же точка М (jc, у) лежит в III квадранте, то абсцисса и ордината будут обе отрицательны, а модули их равны, поэтому будут равны и координаты хм у этой точки. Следовательно, в обоих случаях имеем

Обратно, если координаты х и у какой-нибудь точки М (х, у) удовлетворяют уравнению (2), то эта точка, очевидно, лежит на биссектрисе

I и III координатных углов. Поэтому уравнение (2) представляет собой уравнение биссектрисы I и III координатных углов.

Рассмотрим теперь биссектрису II и IV координатных углов (рис. 18, б). Возьмем на ней произвольную точку N (х, у). В каком бы квадранте — II или IV — ни была расположена эта точка, координаты ее х и у равны по модулю и отличаются знаками.

Следовательно, в обоих случаях имеем

Обратно, если для какой-нибудь точки N (,х, у) выполнено уравнение (3), то эта точка, очевидно, лежит на биссектрисе II и IV координатных углов. Таким образом, уравнение (3) есть уравнение биссектрисы II и IV координатных углов.

Пример:

Составить уравнение прямой, параллельной оси ординат.

Решение:

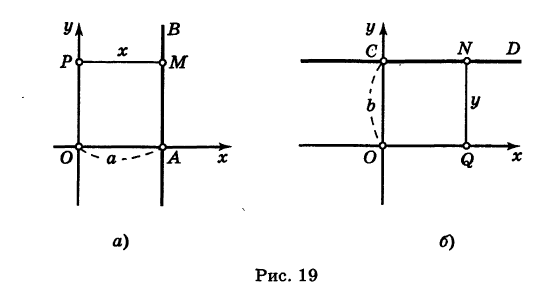
Пусть прямая АВ || О у и пусть отрезок OA = а (рис. 19, а). Тогда для любой точки М (х, у) прямой АВ ее абсцисса х равна а:

Обратно, если абсцисса некоторой точки М (х, у) равна а, то эта точка лежит на прямой АВ.

Таким образом, уравнение (4) представляет собой уравнение прямой, параллельной оси Оу и отстоящей от нее на расстоянии, равном числовому значению а; при этом если прямая расположена справа от оси Оу, то а положительно; если же прямая расположена слева от оси Оу, то а отрицательно.

В частности, при а = 0 получаем уравнение оси ординат: х = 0.

Пример:

Составить уравнение прямой, параллельной оси абсцисс.

Решение:

Совершенно аналогично, если прямая CD || Ох и ОС = Ь (рис. 19, б), то ее уравнение будет

при этом если прямая CD расположена выше оси Оху то Ъ положительно, если же прямая CD расположена ниже оси Ох, то b отрицательно.

В частности, при b = 0 получаем уравнение оси абсцисс: у = 0.

Пример:

Найти линию, расстояние точек которой от точки В (12, 16) в два раза больше, чем от точки А (3, 4).

Решение:

Если М (х, у) — произвольная точка искомой линии, то согласно условию задачи имеем

Чтобы составить уравнение этой линии, надо выразить AM и ВМ через координаты х и у точки М. На основании формулы расстояния между двумя точками имеем

откуда, согласно соотношению (5),

Это и есть уравнение искомой линии.

Но в таком виде трудно судить, какую линию представляет это уравнение, поэтому упростим его. Возведя обе части в квадрат и раскрыв скобки, получим

или после несложных преобразований имеем равносильное уравнение

Сравнивая полученное уравнение с уравнением (1), мы видим, что искомая линия является окружностью радиуса 10 с центром в начале координат.

Видео:Уравнение прямой.Скачать

Построение линии по ее уравнению

Если переменные х и у связаны некоторым уравнением, то множество точек М (х, у), координаты которых удовлетворяют этому уравнению, представляет собой, вообще говоря, некоторую линию на плоскости (геометрический образ уравнения).

В частных случаях эта линия может вырождаться в одну или несколько точек. Возможны также случаи, когда уравнению не соответствует никакое множество точек.

соответствует единственная точка (1, 2), так как этому уравнению удовлетворяет единственная пара значений: х = 1 и у = 2.

не соответствует никакое множество точек, так как этому уравнению нельзя удовлетворить никакими действительными значениями x и у.

Зная уравнение линии, можно по точкам построить эту линию.

Пример:

Построить линию, выражаемую уравнением

(обычно говорят короче: построить линию у = х 2 ).

Решение:

Давая абсциссе х в уравнении (1) числовые значения и вычисляя соответствующие значения ординаты у, получим следующую таблицу:

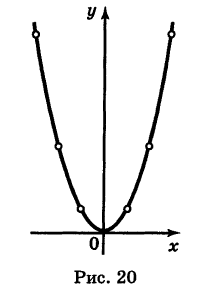
Нанося соответствующие точки на плоскость, мы видим, что конфигурация этих точек определяет начертание некоторой линии; при этом чем гуще построена сеть точек, тем отчетливее выступает ее контур. Соединяя построенные точки линией, характер которой учитывает положение промежуточных точек1*, мы и получаем линию, определяемую данным уравнением (1) (рис. 20). Эта линия называется параболой.

Некоторые элементарные задачи с решением

Если известно уравнение линии, то легко могут быть решены простейшие задачи, связанные с расположением этой линии на плоскости.

Задача 1. Заданы уравнение линии К и координаты точки М (а, Ь). Определить, лежит точка М на линии К или нет.

Иными словами, требуется узнать, проходит линия К через точку М или не проходит.

На основании понятия уравнения линии получаем правило:

чтобы определить, лежит ли точка М на данной линии К, нужно в уравнение этой линии подставить координаты нашей точки. Если при этом уравнение удовлетворится (т. е. в результате подстановки получится тождество), то точка лежит на линии; в противном случае, если координаты точки не удовлетворяют уравнению линии, данная точка не лежит на линии.

Для того чтобы иметь возможность судить о положении промежуточных точек линии, мы должны предварительно изучить общие свойства уравнения этой линии (подробнее см. в гл. XI).

В частном случае линия проходит через начало координат тогда и только тогда, когда уравнение линии удовлетворяется при х = 0 и у — 0.

Пример:

Определить, лежат ли на ней точки М (-3, 4) и N (4, -2).

Решение:

Подставляя координаты точки М в уравнение (1), получаем тождество

Следовательно, точка М лежит на данной окружности.

Аналогично, подставляя координаты точки N в уравнение (1), будем иметь

Следовательно, точка N не лежит на данной окружности.

Задача 2. Найти точку пересечения двух линий, заданных своими уравнениями.

Точка пересечения одновременно находится как на первой линии, так и на второй. Следовательно, координаты этой точки удовлетворяют уравнениям обеих линий. Отсюда получаем правило:

чтобы найти координаты точки пересечения двух линий, достаточно совместно решить систему их уравнений.

Если эта система не имеет действительных решений, то линии не пересекаются.

Пример:

Найти точки пересечения параболы у = х2 и прямой у — 4.

Решение:

получаем две точки пересечения: А (-2, 4) и В (2, 4).

Задача 3. Найти точки пересечения данной линии с осями координат.

Эта задача является частным случаем задачи 2. Учитывая, что уравнение оси Ох есть у = 0, получаем правило: ‘

чтобы найти абсциссы точек пересечения данной линии с осью Ох, в уравнении этой линии нужно положить у = 0 и решить полученное уравнение относительно х.

Аналогично, так как уравнение оси Оу есть х — 0, то получаем правило:

чтобы найти ординаты точек пересечения данной линии с осью Оу, нужно в уравнении этой линии положить д: = 0 и решить полученное уравнение относительно у.

Пример:

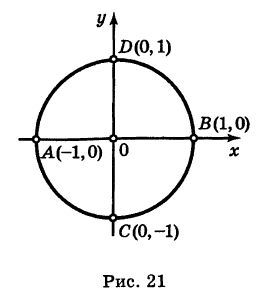
Найти точки пересечения окружности 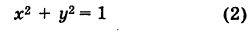с осями координат.

Решение:

Полагая у = 0 в уравнении (2), получаем х2= 1, т. е. х1 = -1 и х2 = 1. Отсюда находим две точки пересечения данной окружности с осью Ох (рис. 21): А (-1, 0) и В (1, 0).

Аналогично, полагая х = 0 в уравнении (2), получаем у2 = 1, т. е. ух = -1 и у2 = 1. Следовательно, имеются две точки пересечения данной окружности с осью Оу (рис. 21): С (0, -1) и D (0, 1).

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Две основные задачи аналитической геометрии на плоскости

Резюмируя содержание этой главы, можно сказать, что всякой линии на плоскости соответствует некоторое уравнение между текущими координатами (х, у) точки этой линии. Наоборот, всякому уравнению между х и г/, где х и у — координаты точки на плоскости, соответствует, вообще говоря, некоторая линия, свойства которой вполне определяются данным уравнением.

Отсюда, естественно, возникают две основные задачи аналитической геометрии на плоскости.

Задача 1 .Дана линия, рассматриваемая как множество точек. Составить уравнение этой линии.

Задача 2. Дано уравнение некоторой линии. Изучить по этому уравнению ее геометрические свойства (форму и расположение).

Алгебраические линии

Определение: Линия называется линией (или кривой) n-го порядка(п = 1, 2. ), если она определяется уравнением п-й степени относительно текущих прямоугольных координат.

Такие линии называются алгебраическими. Например, линии

являются кривыми соответственно первого, второго и третьего порядков.

Общий вид кривых первого порядка есть

где коэффициенты А и Б не равны нулю одновременно, т. е. 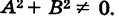Как будет доказано ниже (см. гл. III), все кривые первого порядка — прямые линии.

Общий вид кривых второго порядка следующий:

где коэффициенты А, Б и С не равны нулю одновременно, т. е.

Заметим, что не всякому уравнению второго порядка соответствует действительная кривая. Например, уравнению не отвечает никакая кривая на плоскости Оху, так как, очевидно, нет действительных чисел х и z/, удовлетворяющих этому уравнению.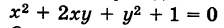

В следующих главах мы подробно изучим кривую первого порядка (прямую линию) и рассмотрим важнейшие представители кривых второго порядка (окружность, эллипс, гипербола, парабола).

Уравнение кривой n-го порядка может быть записано в следующем виде:

где хотя бы один из старших коэффициентов apqt т. е. таких, что p + q = п, отличен от нуля ( 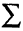— знак суммирования).

Отметим важное свойство: порядок кривой (1) не зависит от выбора прямоугольной системы координат.

Действительно, выбирая другую систему прямоугольных координат О’х’уна основании формул перехода имеем

где 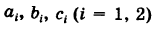— некоторые постоянные коэффициенты.

Отсюда уравнение кривой (1) в новых координатах О’х’у’ будет иметь вид

где п’ — порядок преобразованной кривой. Очевидно, что п’

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Параметрическое задание кривой

Видео:13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Параметрическое задание кривой

• Кривая параметрическая Н°1.Подход к делу problem. So до сих пор мы рассматривали только 2 вида назначений кривых: уравнение v = f (x) (явная задача) или уравнение F (x, y)= O (неявная задача)).Однако теоретическая механика очень естественно приводит к различным видам линий assignments. In дело в том, что

установка движения точки-это средство нахождения положения (то есть координат) любого момента времени t. Чтобы полностью определить движение точки, определите линию, на которой будет находиться точка move. So, в этом примере линии даны с использованием

So например, эквационный х = 2Т г = 3Т-2(1） Людмила Фирмаль

2 равенств (I).Конечно, очень легко получить более знакомые задачи в той же линии. Именно так. Для любого момента x 3x /будет t = — q, t y =-2. Это соединение X и y обеспечивает явное определение линии*).Видно, что эта задача получается путем исключения времени t из Формулы (1). В рассматриваемом

примере, тот факт, что переменная T показывает время не играет никакой роли. Например, предположим, что следующие X и y зависят от вспомогательных переменных: х = Т-ФЛ, г = т Изменение его даст вам различные точки(.x, комбинация которых состоит из нескольких линий. значение t обозначается равенством t = x-1 с соответствующим значением x, поэтому y =(x-I) 1 для

• любой точки линии, и я получил явную задачу линии. Из этого видно, что вы обрабатываете 1 пару болтов. Чтобы суммировать вышесказанное, пара уравнений Где t-вспомогательная переменная, определяющая lnnnu. Способ определения этой линии называется параметрическим, а переменная t называется

параметром. за исключением t, вы получаете нормальное (явное или неявное) уравнение для той же строки. Замечание. Если функция Людмила Фирмаль

и последовательным в интервале[i, b]), является непрерывной кривой, поскольку она также может Параметрические уравнения для окружностей и эллипсов. Рассмотрим окружность с радиусом R, центрированную вокруг начала координат

(рис.181).Положение любой точки M в этой окружности полностью определяется установкой угла f, который образуется осью Ox и радиусом OM. It естественно выразить координаты x и y точки M под этим углом. Из рисунков это сразу понятно (2） х = р COS в ТТ г = РС НТ. Эти уравнения (*) являются параметрическими

уравнениями окружности. Параметр T может быть изменен с-oo на — | — oo, но если вы хотите получить каждую точку круга по 1 разу, достаточно пройти t через зазор. Однако, это более удобно для обработки закрытых пробелов. Так, т, как правило,

изменяется в пределах 0 ^ / ^ 2ir, но точка с получает в 2 раза. T= 0 и в = 2ir. Чтобы получить нормальное уравнение окружности, необходимо исключить параметр T из (2).Это проще всего, если вы возьмете уравнение (2) на 2 квадрата и добавите результат. Очевидно, это приводит к известному уравнению Найти

параметрическое уравнение эллипса (3） Полезно помнить, что он получается из круга * * + > ■ = A (4)рисунок 181. Имеют диаметр с большой осью эллипса, иногда используют сжатие、 То есть любая точка M в эллипсе(3) берется из точки N в окружности (4). Б Ордината точки Н В соответствии с вышеизложенным

параметрическое уравнение окружности(4) имеет вид x = acos/, ^ = asin/.Но тогда понятно, что параметрическое уравнение (3) эллипса получается умножением. форма ординаты y имеет вид） (5） * = acosf, г = БС НТ. Чтобы получить все точки овала, достаточно

изменить Т выпускного вечера. Жуткий 0 ^ t ^кроме того, каждая точка эллипса, кроме точки (a, 0), получается только 1 раз, а точки(a, 0) — 2 раза (t = 0 и t = 2k).Если мы разделим первое уравнение (5) на a, а затем разделим 2-е уравнение на b, то полученное уравнение будет добавлено на 2 и станет каноническим уравнением эллипса(3).

Сравнение параметрических уравнений окружности и эллипса дает удобный метод построения любого числа точек в эллипсе. То есть, пара уравнений х-acoet, у = грех Т(6） U определяет окружность с радиусом A вокруг начала координат и пару уравнений х = б сое т, у = B грех Т(7） — Окружность b с тем же центром и радиусом; чтобы получить точку (l, y), как показывает уравнение (5), p / 82.Если

вы лежите на овале, вам нужно найти x Используйте первое выражение(6) и 2-е выражение (7) с y. но эти xn-y легко найти графически, так как в формулах (6) и (7) параметром T является угол наклона радиус-вектора точки относительно оси Ox. So, чтобы составить точку M (q, y) эллипса (5), нарисуйте окружность (6) и (7)

и нарисуйте луч на оси Ox под углом t от начала координат. Найдите точки A и B пересечения этого луча и ранее упомянутой окружности и проведите через них прямую линию, параллельную оси, вы получите точку M (см. Рисунок 182).П°3.Циклоида * важные

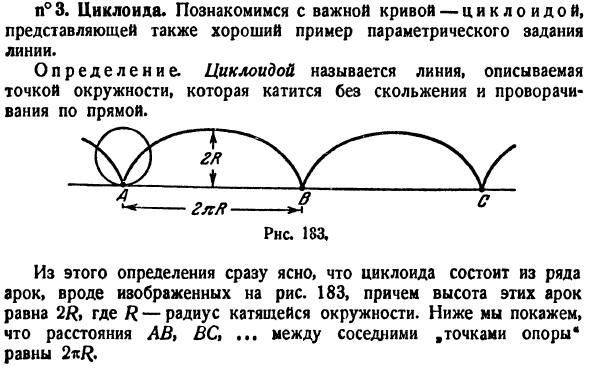
кривые-давайте познакомимся с циклоидой. Это также хороший пример параметрического определения линии. Определение циклоида представляет собой линию, которая представлена точкой окружности, которая катится без скольжения или вращения Из этого определения сразу видно, что циклоида состоит из ряда дуг, как

показано на рисунке 1. 183, высота этих арок равна 2R. R-радиус окружности. Ниже расстояние между соседними точками разворотаAB, BC,…равно 2π/?Это значение по умолчанию. Найдите параметрические уравнения циклоиды. В качестве оси Ox возьмите прямую линию, по которой катится круг, и для начала координат

возьмите положение точки M, которая представляет собой циклоиду острия в этой точке. Эта точка находится на оси Ox. Нарисуйте этот момент как первый момент, вращающийся круг в первый момент, а затем второй. t представляет собой угол, образованный в момент t радиусом вращающейся окружности, направленной

к точке A окружности, которая касается точки I и оси Ox, представляющей циклоиду. (Рисунок 184) радиус CXM и u ° С / а возьмем этот угол т. 184. Попробуйте параметр 8a Через него отрегулируйте точки x и y м-циклоиды. Что касается координат Y, то это довольно просто. г => ВМ = объявление = ОБК-CjZ)= /? — R cos t.

(8） Чтобы найти абсциссу X, нужно рассмотреть эквивалентность отрезка OA и дуги AM. OA = AM. (9 )） При таком равенстве окружность не будет скользить или вращаться. Следующий метод проверки эквивалентности очень очевиден(9): представьте себе катящийся круг, выполненный в виде деревянного кольца. Накройте этот обруч лентой, которая не растягивается, прибив ее правый край гвоздем

к точке O оси Ox, а левый край-к обручу. При вращении обруча лента начинает растекаться по оси Ox, и в момент t отсечение оси OA закрывается той частью ленты, которая упала вниз. С дугой AM обруч. Это*) доказывает(9). еще проще: t-значение угла AC% M, так как это Радиан、 AM = Rt Так… x = OB = OA-BA = AM-MD = Rt-Rsint (10） Если

сравнить (8)и(10), то получим параметрическое уравнение циклоиды х = р(т-Син т), г = р (- стоимость). Параметр Т может изменяться от-ОО до-Е-ОО. Пересечение начала координат и ближайших к нему справа циклоид соответствует значению Ox = t * 2.Это происходит потому, что круг качения приобретается после 1 rotation. In в этом случае

t будет n; = 2nR. In кроме того, из (11) видно, что координаты (π/,, 2/) находятся в высшей точке соответствующего cycloid. To будьте осторожны невозможно представить Y в качестве одной из основных функций Икс. И от x до y возможно| f = Arccos ^ l, но результат Формула очень трудоемкая. Параметрическое уравнение

проще. в N°4.Эвольвента circle. In в теории зацепления используется кривая, называемая эвольвентой окружности. Эвольвента окружности определения-это линия, которая описывается точкой нити и расстегивается от этой окружности, пока она прочно растянута. Предполагается, что нить неэластична и предварительно обмотана вокруг вышеуказанных кругов. Найти параметрическое

уравнение для эвольвенты circle. To сделайте это, поместите начало координат в центр круга и нарисуйте ось Ox Ноль ноль В тот момент, когда нить еще полностью обмотана вокруг окружности, точка окружности, в которой расположена точка, описывающая эвольвенту. Рисунок 185 эта точка обозначается A. 185 показывает положение потока виртуальной машины в некоторой точке в time. So, здесь B-

точка, в которой нить исчезает из окружности, а M-точка, в которой она описывает эвольвенту. Радиус окружности? Угол наклона оси Ox и Луча OB представлен через t. поскольку нить не является растяжимой、 Отрезок VM равен дуге AB окружности. То есть, BM = RT. обратите внимание, что нить остается прочно натянутой, поэтому она спускается по касательной от окружности. Таким образом,

нить VM перпендикулярна радиусу органического вещества. Поэтому углы AOB и MBD равны углам, где каждая сторона перпендикулярна друг другу. Следовательно,£МБД = T, и из треугольника МВС См = РТ грех ЦБ = стоимость РТ. Теперь вы можете легко найти X и y координаты точки м. Другими словами、 х = ое = ОД + де = ОД-ТСМ = стоимости Р + РТ грех г = ВС = ДК = ДБ-КБ = Р грех Т-РТ стоимость. Рисунок 185.Наконец. х = /?(потому что * — Ф — * грех/),; г = р (т Син-/ Кос Т), (’ Где: 0 f > = » K0(13） В точке M (x, y), соответствующей значению параметра T. To сделайте это, дайте

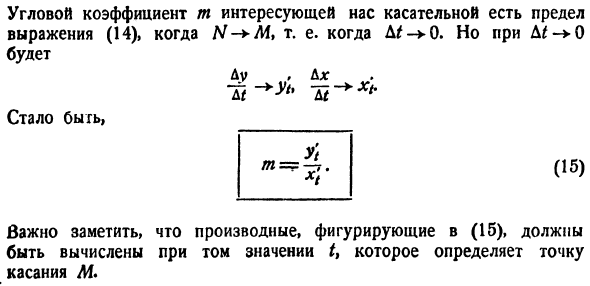
t приращение At и в результате получите ту же самую точку кривой AfCtf-J-A * » Y + AC) (13).Угловой коэффициент Т * Секущий MN равен или равен Важно отметить, что производная, фигурирующая в (15) , должна быть рассчитана для величины t, определяющей контакт M. Угловой коэффициент m интересующего тангенса является

пределом формулы (14) для N — + M, то есть, но так как D * — > 0 Вы будете Работать ДД： (15 )） Так… Образцы. Нарисуйте касательную к кривой + г = Тл-7т(16） Очки*)А!(2). Решение. Координаты точки M определяются из(16). xi = 17, y%=2.In сложение, x = bP—4/, y = 4P-7.So, t = 2 — Это X / = 20, yt = 25, угловой коэффициент Желаемый тангенс. Форма искомого уравнения имеет вид y-2 = 4 (l-17> Замечание.

Приведенная выше строка g:=?( * ), Y =φ (f), функция равна (t), φ (/).Если эти функции не только непрерывны, но и имеют непрерывные производные от y’0, то, как показывает уравнение (15), кривая имеет определенную касательную в каждой точке, и ее положение непрерывно изменяется с изменением контакта.

Кроме того, указанные касательные никогда не будут параллельны оси Oy. Учитывая, что координаты x и y полностью равны, линии x =

.Где f (/j u f ( / ) имеет непрерывную производную、 а В частности, под это определение подпадает линия y = f ( * ), где f (x) имеет непрерывную производную. Где роль параметра T-абсцисса ш=■»+*?> ми- Теперь зададим следующие общие вопросы: пусть

x и y зависят от вспомогательных переменных t, как показано в (13). в первом выражении (13) обозначим t из x, а затем присвоим его 2-му выражению, вы увидите, что y является функцией x, то есть y = f(x).Попробуйте найти производную этой функции. Для этого достаточно вспомнить, что интересующей нас производной является только угловой коэффициент касательной прямой y = / ( * ),

а ее параметрическим уравнением является уравнение (13).Таким образом, она задается формулой(15). Чтобы правильно понять это важное выражение, следует помнить, что точка дифференцирования t справа от (17) является значением параметра, и согласно формуле x = y (t) она соответствует точке дифференцирования x, где Y’x находится. Соотношения(17) легко получить с помощью чисто формальных

вычислений. dypy / ДТ Вау, х]’ Затем попробуйте найти 2-ю производную yx той же функции y = f (x).Это легко сделать, используя формулу (17).То есть он временно представляет y’X с Z. А затем… ** ух-з» (17) Значение (18） Однако, поскольку Z = yx = — m、 / ГМ-ГМ Узнайте, наконец, из (18)и (19) Образцы. Установите вогнутое направление

кривой х =(* + 3Т + л> г = 2Т * — (21） В точке Af (l). Решение. Из (21), x’f = 2t + 3, x? = 2,г = г г! = 12 /.Итак, если t = 1, то это выглядит так:= jc / = 2, y ’ 0, кривая точки M (21) направлена вогнутой поверхностью вверх.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

🎬 Видео

11. Прямая в пространстве и ее уравненияСкачать

УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Уравнение прямой #уравнениепрямой #графикифункции #линейнаяфункция #графикиогэСкачать

Математика без Ху!ни. Уравнение касательной.Скачать

Написать канонические и параметрические уравнения прямой в пространствеСкачать

14.1. Касательная к параметрически заданной функцииСкачать