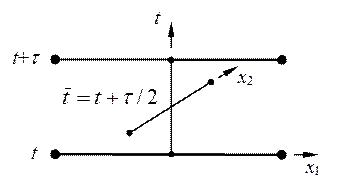Видео:Решение уравнения теплопроводности в одномерной постановке в Excel с применением неявной схемыСкачать

Содержание
Видео:Решение задачи теплопроводности (Явная разностная схема)Скачать

Постановка задачи [ править ]
Необходимо решить задачу Коши для двумерного уравнения теплопроводности (дифференциальное уравнение в частных производных второго порядка, которое описывает распределение температуры в заданной области пространства и его изменение во времени.) с использованием средств параллельного программирования на основе MPI. Задача решается для однородного уравнения теплопроводности (система теплоизолирована) в области [0..L]x[0..L]:
[math]frac — a^2(frac+frac) = 0[/math]
[math]U(t=0) = U_0[/math]
при граничных условиях:
[math] U(x,y,t) = beginT_0, x=0\ T_1, x!=0 end[/math]
Используемые величины параметров:
[math]L=1, T_0=100, T_1=0[/math]
Видео:Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Используемый метод [ править ]
В вычислительных системах с распределенной памятью процессоры работают независимо друг от друга. Для организации параллельных вычислений в таких условиях необходимо иметь возможность распределять вычислительную нагрузку и организовать информационное взаимодействие (передачу данных) между процессорами. Параллельное программирование служит для создания программ, эффективно использующих вычислительные ресурсы за счет одновременного исполнения кода на нескольких вычислительных узлах. Для создания параллельных приложений используются параллельные языки программирования и специализированные системы поддержки параллельного программирования, такие как MPI и OpenMP. Итак, MPI — это библиотека передачи сообщений, собрание функций на C/C++ (или подпрограмм в Фортране), облегчающих коммуникацию (обмен данными и синхронизацию задач) между процессами параллельной программы с распределенной памятью. Акроним MPI установлен для Message Passing Interface (интерфейс передачи сообщений). Под параллельной программой в рамках MPI понимается множество одновременно выполняемых процессов. Все процессы порождаются один раз, образуя параллельную часть программы. Каждый процесс работает в своем адресном пространстве, никаких общих переменных или данных в MPI нет. Процессы могут выполняться на разных процессорах, но на одном процессоре могут располагаться и несколько процессов (в этом случае их исполнение осуществляется в режиме разделения времени).
Видео:01 Теплопроводность, явныйСкачать

Реализация [ править ]
При решении поставленной задачи будем использовать замену частных производных в дифференциальных уравнениях их разностными аналогами. Сеточный метод, основанный на замене в дифференциальном уравнении производных конечными разностями, называют методом конечных разностей, а сеточную схему такого метода — конечно-разностной.
По аналогии с одномерной задачей для уравнения теплопроводности вводим явную конечно-разностную схему. Область [0..L]x[0..L] разбивается на подобласти согласно количеству процессов в выполняемой параллельной программе. На каждом полученном таким способом интервале процесс интегрирования осуществляется отдельным процессом, при этом в связи с использованием явной схемы соседние процессы должны обмениваться крайними значениями, полученными на предыдущем шаге, для выполнения следующего шага.
Программа для решения двумерного уравнения теплопроводности: программа
Видео:Решение нестационарного уравнения теплопроводности в двухмерной постановке в ExcelСкачать

Результаты [ править ]
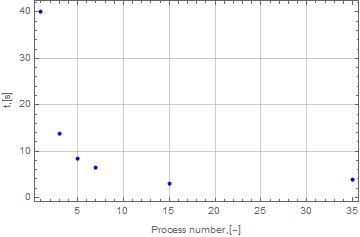
Найдено решение однородного уравнения теплопроводности в двумерной постановке для следующей сетки узлов: 300х300.
| Количество процессов [-] | Время рассчета [сек] |
|---|---|
| 1 | 40.2082 |
| 3 | 13.7626 |
| 5 | 8.38831 |
| 7 | 6.56195 |
| 15 | 3.08675 |
| 35 | 3.90614 |
Показано, что при увеличении количества процессов уменьшается время расчета. Также из приведенного графика видно, что для малого числа узлов в сетке использование большого количества процессов не обосновано — выигрыш во времени либо незначителен, либо же затраченное время увеличивается.
Видео:Решение задачи теплопроводности методом конечных разностейСкачать
Уравнение теплопроводности
Ранее (см. разд. 2.1.2, 2.1.3) уже были построены и исследованы разностные схемы решения смешанной задачи для одномерного уравнения теплопроводности:

Были получены две двухслойные схемы — явная (2.3) и неявная (2.4). В явной схеме значения сеточной функции 
Неявная схема безусловно устойчива, явная схема устойчива при выполнении условия
Обе схемы сходятся к решению исходной задачи со скоростью 
Схемы (2.3), (2.4) построены для случая, когда значения искомой функции (температуры) Uна границах х = 0, х = 1определяются заданными функциями 
В этом случае, как и при решении волнового уравнения, данное условие нужно записывать в схемах (2.3), (2.4) в разностном виде.
Перейдем теперь к построению разностных схем для уравнения теплопроводности с двумя пространственными переменными. Примем для простоты а = 1. Тогда это уравнение можно записать в виде

Пусть при t=0 начальное условие задано в виде

В отличие от волнового уравнения, требующего два начальных условия, в уравнение теплопроводности входит только первая производная по t, и необходимо задавать одно начальное условие.
Часто задачи теплопроводности или диффузии, описываемые двумерным уравнением (2.76), решаются в ограниченной области. Тогда, кроме начального условия (2.77), нужно формулировать граничные условия. В частности, если расчетная область представляет прямоугольный параллелепипед 


Рис. 2.24. Расчетная область
Введем простейшую сетку с ячейками в виде прямоугольных параллелепипедов, для чего проведем три семейства плоскостей: хi= ih1(i=0,1. I), 



Рассмотренные выше схемы для одномерного уравнения легко обобщаются на двумерный случай.
Построим явную разностную схему, шаблон которой изображен на рис. 2.25. Аппроксимируя производные отношениями конечных разностей, получаем следующее сеточное уравнение:
Рис. 2.25. Шаблон двумерной схемы
Отсюда можно найти явное выражение для значения сеточной функции на (k + 1)-ом слое:

Условие устойчивости имеет вид

При 

Полученная схема сходится со скоростью
Формулы (2.78) или (2.80) представляют собой рекуррентные соотношения для последовательного вычисления сеточной функции во внутренних узлах слоев k = 1,2. К. На нулевом слое используется начальное условие (2.77), которое записывается в виде

Значения 
Алгоритм решения смешанной задачи для двумерного уравнения теплопроводности изображен на рис. 2.26. Здесь решение хранится на двух слоях: нижнем (массив 

Рис. 2.26. Алгоритм решения двумерного уравнения теплопроводности
Построим теперь абсолютно устойчивую неявную схему для решения уравнения (2.76), аналогичную схеме (2.4) для одномерного уравнения теплопроводности. Аппроксимируя в (2.76) вторые производные по пространственным переменным на (k + 1)-ом слое, получаем следующее разностное уравнение:

Это уравнение можно записать в виде системы линейных алгебраических уравнений относительно значений сеточной функции на каждом слое:

К этой системе уравнений нужно добавить граничные условия для определения значений сеточной функции в граничных узлах (т.е. при i= 0, I; j = 0, J). На нулевом слое решение находится из начального условия (2.77), представленного в виде (2.81).
Система (2.83), полученная для двумерного уравнения теплопроводности, имеет более сложный вид, чем аналогичная система (2.22) для одномерного случая, которую можно решить методом прогонки. Таким образом, распространение неявной схемы на многомерный случай приводит к значительному усложнению вычислительного алгоритма и увеличению объема вычислений.
Недостатком явной схемы (2.78) является жесткое ограничение на шаг по времени τ, вытекающее из условия (2.79). Существуют абсолютно устойчивые экономичные разностные схемы, позволяющие вести расчет со сравнительно большим значением шага по времени 
Видео:Решение уравнения теплопроводности методом конечных разностейСкачать

Многомерное уравнение
Экономичные схемы. Для уравнения переноса (лекция №10) хорошие схемы бегущего счета естественным образом обобщаются на многомерный случай. Для уравнения теплопроводности попытки обобщить хорошие неявные разностные схемы типа (6), (19),(20) на многомерный случай сталкиваются с принципиальными трудностями.
Рассмотрим эти затруднения на примере двумерного уравнения теплопроводности с постоянным коэффициентом теплопроводности, для которого определена первая краевая задача в прямоугольной по переменным x1, x2 области:
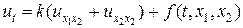
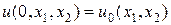

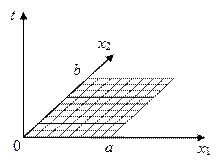 | 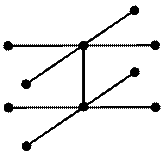 |
| Рис.6,а. Определение прямоугольной равномерной сетки с шагами h1, h2 по переменным x1, x2 | Рис.6,б. Шаблон разностной схемы (37) |
Определим прямоугольную сетку (x1,n,x2,m) (рис.6,а), считая для простоты ее равномерной с шагами по переменным x1, x2 — h1, h2 соответственно, т.е. x1,n = h1n, x2,m = h2m, n = 0,1,…,N, m = 0,1,…,M. Выберем в качестве шаблона разностной схемы тот, который представлен на рис.6,б. На каждом временном слое шаблон имеет форму креста, по которому составляется неявная двухслойная схема с весом s, построенная по аналогии со схемой (6), т.е.
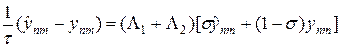
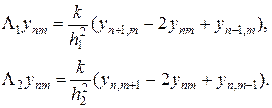
Запись начального (35) и краевых условий (36) в разностном виде очевидна и реализуется точно. Можно проверить, что погрешность аппроксимации схемы (37), (37¢) на решениях с непрерывными четвертыми производными равна 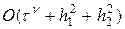
Исследуем устойчивость разностной схемы (37), (37¢) методом разделения переменных. Гармоники с текущего и следующего временного слоя выберем в виде:
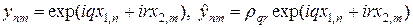
тогда, считая как обычно модуль множителя роста 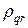
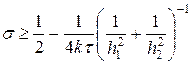
которое похоже на аналогичное условие (10) для одномерной схемы (6).
Схема (37), (37¢) легко обобщается на случай p измерений. Оценим число операций, требуемых для расчета до момента времени T.
Рассмотрим явную схему при s = 0, для которой значения 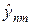
N p операций, где для простоты считается, что число узлов по каждой переменной одинаково и равно N. Согласно (38), явная разностная схема устойчива, когда
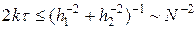
Таким образом, для расчета до момента времени T необходимо сделать
N 2 шагов по времени и полный расчет потребует
Если пользоваться абсолютно устойчивой схемой, когда s ³ ½, то можно выбирать t
h. Однако, в этом случае необходимо решать линейную систему уравнений порядка N p . Если ее решать методом Гаусса, то потребуется
N 3 p операций. Это число операций можно несколько сократить, заметив, что полученная матрица будет сильно разреженной и если предположить, что используется алгоритм, учитывающий такую разреженность, то число операций будет
N 3 p — 2 . Такая оценка следует из того, что в одномерном случае матрица трехдиагональная и система уравнений решается прогонкой с числом операций
N. Учитывая, что для получения решения в момент времени T требуется
N шагов по времени, найдем итоговую оценку для числа операций
N 3 p — 1 при использовании неявной разностной схемы.
Если для одномерного уравнения явная схема является явно невыгодной на фоне использования неявных схем, то в многомерном случае (p ³ 2) неявные схемы становятся невыгодными по сравнению с явной схемой.
Несмотря на упомянутые выше трудности, для многомерного параболического уравнения построены абсолютно устойчивые разностные схемы, которые позволяют вести расчет с шагом t
N p операций для перехода со слоя на слой. Это значит, что число действий в расчете на узел пространственной сетки не зависит от шагов ha, a = 1,…,p. Такие схемы принято называть экономичными.
Подавляющее большинство многомерных расчетов параболических уравнений производится по экономичным схемам. Ниже будут рассмотрены два вида таких схем: продольно-поперечные и локально-одномерные.
Продольно-поперечная схема является одной из самых лучших двумерных экономичных разностных схем. Ее также называют схемой переменных направлений. На рис.7 приведен шаблон схемы переменных направлений, в которую введен полуцелый слой 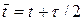
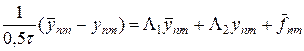
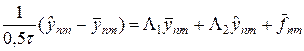
где разностные операторы L1, L2 определены в (37¢), а 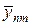
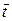
Рис.7. Шаблон разностной схемы (39), (39¢)
Исследуем продольно-поперечную разностную схему (39), (39¢).
Вычислительная процедура по схеме (39), (39¢) складывается из перехода со слоя t на слой 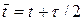
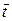
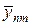
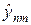
Устойчивость продольно-поперечной схемы можно исследовать методом разделения переменных. Положим
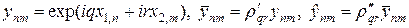
где 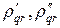
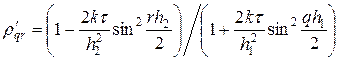

Учитывая (40), (41¢), можно убедиться, что для любых гармоник и при любых шагах сетки верно неравенство: 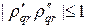
Порядок аппроксимации схемы (39), (39¢) можно оценить путем исключения полуцелого слоя. Для этого вычтем из уравнения (39) уравнение (39¢), тогда найдем
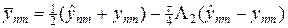
Складывая уравнения (39), (39¢) и подставляя в них выражение (42), получим
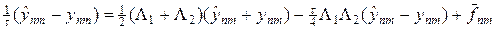
Предпоследний член в правой части (43), после разложения в ряд Тейлора, может быть аппроксимирован выражением 
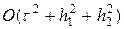
Определимся с аппроксимацией граничных условий (36) для продольно-поперечной схемы. При решении уравнения (39¢) относительно 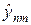
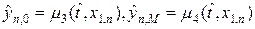
При решении уравнения (39) относительно 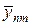
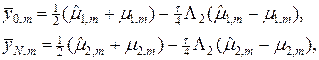
где m = 1,…,M-1. Граничные условия (44), (44¢) обеспечивают погрешность аппроксимации 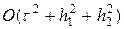
Проведенное исследование аппроксимации и устойчивости показывает, что схема (39), (39¢) безусловно сходится в норме 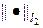
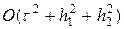
Изучим разностную схему (39), (39¢) на примере численного решения уравнения (34) с правой частью вида:
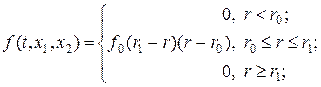
где f0, r0, r1 = const > 0, а 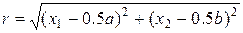
%Программа решения двухмерного уравнения
%теплопроводности (34) с источником специального
%вида (45) с помощью продольно-поперечной
%разностной схемы (39), (39′)
global a b f0 r0 r1
%Определяем габариты области интегрирования
%по времени, направлениям x1 и x2, а также
%коэффициент теплопроводности и константу f0,
%задающую амплитуду источника
T=1; a=1; b=1; koef=0.5; f0=100;
%Определяем число шагов по времени и по
%направлениям x1 и x2
%Определяем сетки по x1 и x2
%Определяем источник тепла в узлах сетки
%Рисуем трехмерный профиль источника тепла
%Определяем нулевые начальные данные
%Определяем граничные условия при x1=0 и x1=a
%Определяем граничные условия при x2=0 и x2=b
%Определяем номера слоев по времени, которые будут
%нарисованы на итоговом графике
%Организуем основной цикл интегрирования по времени
%Находим решение на полуцелом временном слое,
%т.е. решаем уравнение (39)
%Учитываем нулевое граничное при x1=0
%Учитываем нулевое граничное при x1=a
%Находим решение на следующем временном слое,
🌟 Видео
Решение уравнения теплопроводности в одномерной постановке в ExcelСкачать

8.1 Решение уравнения теплопроводности на отрезкеСкачать

Решение задачи Коши для уравнения теплопроводности (Часть 1)Скачать

Уравнение в частных производных Уравнение теплопроводностиСкачать

12. Как остывает шар (решение уравнения теплопроводности)Скачать

Численные методы математической физики - Решение смешанной задачи для уравнения теплопроводностиСкачать

Решение задач теплопроводности (короткая версия)Скачать

Уравнение теплопроводности на полупрямой (решение задачи)Скачать

Уравнение теплопроводности. Операционный методСкачать

Принцип максимума для уравнения теплопроводности на отрезкеСкачать

12.1 Как остывает кирпич (уравнение теплопроводности)Скачать

6-1. Уравнение теплопроводностиСкачать

Решение задач теплопроводности (часть 1)Скачать